Cuando se juega de acuerdo con las reglas est谩ndar de Gomoku, las negras no necesitan m谩s de
35 movimientos para ganar. El art铆culo presenta a su atenci贸n una estrategia ganadora completa y el algoritmo correspondiente del juego.
Demostraci贸n de la soluci贸n completa,
aqu铆 , puedes jugar y encontrar las opciones m谩s largas. El programa siempre gana y gasta en 茅l no m谩s de 35 movimientos. El c贸digo fuente de la aplicaci贸n, la soluci贸n en s铆 y ejemplos de partes al final del art铆culo.
No me detendr茅 en las reglas y t谩cticas del juego. El tema se discuti贸 en detalle sobre habr
aqu铆 , as铆 como los algoritmos de decisi贸n
aqu铆 y
aqu铆 .
Peque帽a digresi贸n
Antes de la era de los tel茅fonos inteligentes, el tic-tac-toe "cinco en una fila" (Gomoku, Renju) era uno de los asesinos m谩s populares de la 茅poca en las clases escolares. Considerar combinaciones fue m谩s interesante que el desarrollo de la econom铆a nacional del norte de 脕frica o la clasificaci贸n de las flores de tr茅bol.
En el oto帽o de 1985, las ni帽as de nuestro d茅cimo grado fueron sacadas de una clase de matem谩ticas. Nosotros, los seis ni帽os restantes, ten铆amos m谩s probabilidades de tener comunicaci贸n informal con un maestro de matem谩ticas sobre temas abstractos. La maestra entr贸 al aula en silencio, entreg贸 folletos a todos en una caja y comenz贸 a escribir los nombres de los presentes en la pizarra. Est谩bamos deprimidos, se planific贸 un trabajo independiente o se realiz贸 una encuesta blitz. Pero la lista en el tablero se convirti贸 en una clasificaci贸n y nos anunciaron las reglas del campeonato. Cada uno con cada serie de cinco fiestas. Premio al ganador: cinco a la revista. Seg煤n los resultados del torneo, tuve la suerte de ganar, pero el juego no termin贸 all铆. El maestro prometi贸 ponerle cinco a todos los chicos si el ganador gana los cinco juegos de la serie seguidos. El derecho del primer movimiento se le otorga al ganador. Contrariamente a la afirmaci贸n de nuestro maestro de que con tal condici贸n, con el juego correcto, puedes ganar 10, 100 o cualquier n煤mero de juegos seguidos, la victoria me pareci贸 una suerte incre铆ble.
Nueve a帽os despu茅s, en 1994, el Dr. Lewis Victor Allis declar贸 la evidencia de esta hip贸tesis en un art铆culo de
Go-Moku y Threat-Space Search . El autor no public贸 su estrategia ganadora, que le permite verificar la prueba. Sin embargo, en su libro de 1996
Buscando soluciones en juegos e inteligencia artificial , se proporcion贸 una descripci贸n general de los algoritmos. En conclusi贸n, mencionamos por separado el procedimiento para verificar la integridad de una estrategia ganadora, que se basa en la correcci贸n de la implementaci贸n del algoritmo de b煤squeda para la "secuencia de amenazas" y el an谩lisis de las opciones de contrajuego del oponente.
Los ejemplos de soluciones dadas en el art铆culo y el libro con los "movimientos correctos" de los oponentes, que son parte de una estrategia ganadora, demuestran la debilidad del algoritmo utilizado.
Por ejemplo, en la figura, la soluci贸n del programa para las reglas est谩ndar de Gomoku. Si las negras responden con j10 y luego j8 en respuesta al d茅cimo movimiento g9 de las blancas, el juego termina en 29 movimientos en lugar de 45. Luego, el programa dos veces "no not贸" la combinaci贸n de la "secuencia de amenazas" de las negras en 17 movimientos despu茅s del 16 y despu茅s del 26- El movimiento de las blancas. Y al final, si las blancas hacen el 36潞 movimiento f12 en lugar de j12, aguantar谩 al menos hasta el 49潞 movimiento. Para ser justos, debe decirse que en este ejemplo, todos los movimientos de las negras no le dan a las blancas ninguna posibilidad de terminar el juego a su favor.
En Internet, encontr茅 varias referencias a trabajos similares en busca de una estrategia ganadora. La cuesti贸n de la optimizaci贸n de las soluciones encontradas sigue sin resolverse. 驴Cu谩l es el n煤mero m铆nimo de movimientos que las negras necesitan para ganar?
Entonces, teniendo un poco de tiempo libre, recursos inform谩ticos modernos y rindiendo homenaje a los pasatiempos de los ni帽os 33 a帽os despu茅s del memorable campeonato escolar, se propuso la tarea de encontrar la estrategia ganadora 贸ptima para Black en Gomoku.
Digitalizar la posici贸n en el tablero
Grabar una parte es bastante primitivo. Solo hay 225 celdas en el campo. En consecuencia, cada celda est谩 codificada por 1 byte. Para grabar un lote de 35 movimientos, solo se requieren 35 bytes. Pero dicho registro no es adecuado para la evaluaci贸n de la posici贸n por dos razones: se puede obtener la misma posici贸n en una secuencia diferente de movimientos y no se tienen en cuenta las posiciones sim茅tricas.
Lograr el objetivo del juego (construir cinco piedras seguidas) se puede llevar a cabo en una de las cuatro direcciones: vertical, horizontal y dos diagonales. Por lo tanto, podemos representar cualquier posici贸n como un conjunto de l铆neas. L铆neas horizontales y verticales con una longitud de 15 celdas y l铆neas diagonales con una longitud de 1 a 15 celdas. Cada movimiento cambia el valor de 4 l铆neas en diferentes direcciones a la vez.
La tarea de evaluar una posici贸n es determinar todas las cifras significativas para cada l铆nea. Para simplificar, describimos cada celda de la l铆nea con 2 bits. El primer bit est谩 lleno cuando se instala una piedra blanca, el segundo bit es una piedra negra. Cada l铆nea no contiene m谩s de 15 celdas y est谩 codificada en un entero de 32 bits. Por lo tanto, la b煤squeda de formas en una l铆nea se reduce a comparar el valor num茅rico de la l铆nea a trav茅s de una ventana deslizante con el patr贸n de bits de la forma.
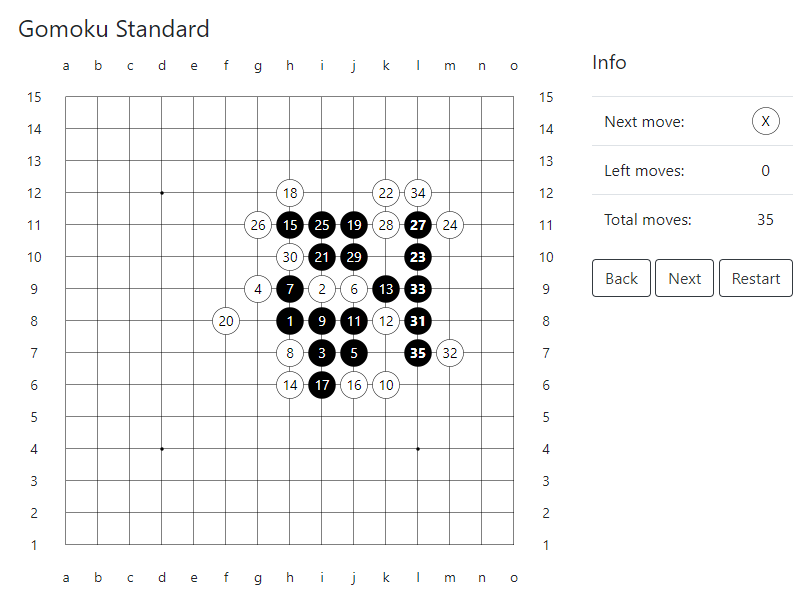
En el ejemplo que se muestra en la figura, la posici贸n se describe con 26 l铆neas. En consecuencia, est谩 codificado con 104 bytes, mientras que un registro de lote regular requiere solo 17 bytes.
Es f谩cil adivinar que todas las simetr铆as (giros e im谩genes especulares) se obtienen simplemente cambiando el n煤mero (barajado) y la direcci贸n de las l铆neas. Para identificar una posici贸n y buscar r谩pidamente colecciones, este principio implementa una funci贸n hash de 32 bits que proporciona diferentes valores solo para posiciones asim茅tricas.
El uso de simetr铆as reduce significativamente el n煤mero de posiciones consideradas. Por ejemplo, el n煤mero de opciones para el segundo movimiento se reduce de 224 a 35.
Al buscar soluciones y combinaciones (esto se discutir谩 m谩s adelante), las posiciones calculadas forman los v茅rtices del gr谩fico multicapa. Los v茅rtices se agrupan en capas seg煤n el n煤mero de celdas rellenas. Los movimientos forman los bordes del gr谩fico, conectando los v茅rtices de las capas adyacentes. Cuando se descartan movimientos fallidos durante la b煤squeda, los bordes se eliminan y algunos de los v茅rtices pierden su conectividad con la rama principal. Por lo tanto, despu茅s de los pasos de c谩lculo, se realiza la recolecci贸n de basura (o la reconstrucci贸n del gr谩fico desde la parte superior).
Durante el proceso de desarrollo, se consideraron varios algoritmos de codificaci贸n, pero el descrito anteriormente mostr贸 la tasa m谩s alta de estimaci贸n de posici贸n.
Evaluar posici贸n
Un factor importante para evaluar una posici贸n es lo importante que los oponentes construyeron las piezas significativas.
Cinco : si tal pieza se encuentra en el tablero, el juego termina. Para las reglas est谩ndar, no seises, sietes, etc., dale un premio a Gomoku. Por lo tanto, las cinco, como, por cierto, todas las dem谩s figuras, requieren la ausencia de sus piedras en las celdas vecinas en una l铆nea.
Las cuatro abiertas : la longitud de 6 celdas, las cuatro del medio est谩n ocupadas por piedras del mismo color, las externas est谩n necesariamente vac铆as. Bueno, en cuanto a cinco, sus piedras est谩n ausentes en las c茅lulas vecinas. Una figura muy fuerte significa ganar incluso en el movimiento de otra persona.
Cuatro : la longitud de 5 celdas, una (cualquiera) de las cinco celdas es libre. Da una victoria por s铆 mismo. Crea una amenaza y obliga al oponente a hacer un movimiento en una celda libre si no tiene sus cuatro. Da 5 puntos en la calificaci贸n de la posici贸n durante la defensa.
Un triple abierto : la longitud de 6 o 7 celdas, las celdas m谩s externas son necesariamente libres. Para 6 celdas, tres de las cuatro centrales est谩n ocupadas por piedras del mismo color, una libre. Para 7 celdas, tres medianas est谩n ocupadas por piedras del mismo color. Una pieza a su vez se convierte en un cuatro abierto si el oponente no tiene un cuatro o un tres abierto. En el movimiento de otra persona, crea una amenaza y obliga al oponente a cerrar los tres o poner sus cuatro en respuesta. El triple de la sexta celda tiene 1 movimiento de subida y 3 movimientos de cierre. El triple de la s茅ptima celda tiene 2 movimientos de subida y solo 2 movimientos de cierre. Da de 2 a 4 puntos en la calificaci贸n de posici贸n.
Un triple , o un triple cerrado, tiene una longitud de 5 celdas, tres de las cuales est谩n ocupadas por piedras del mismo color. Los tres a su vez pueden convertirse en cuatro y se usan en ataque y defensa, creando una amenaza m谩s que un tres abierto del oponente. Da 1 punto en la calificaci贸n de posici贸n.
Un deuce abierto (perspectiva): de 6 a 7 celdas de largo. Al atacar, se convierte en un abierto tres. Da 1 o 2 puntos en la calificaci贸n de posici贸n.
Un enchufe es al mismo tiempo dos o m谩s amenazas que no se pueden cerrar de una vez. Hay tenedores 3x3 (dos triples abiertos), 3x4 (tres y cuatro abiertos) y tenedores 4x4 (dos abiertos). Las horquillas dan una victoria si el oponente no tiene una amenaza mayor: un cuatro o tres abiertos para una horquilla 3x3, o el oponente no puede cerrar la horquilla sucesivamente, creando grandes amenazas: una secuencia de cuatro patas para una bifurcaci贸n de 3x3.
Combinaci贸n : una secuencia continua de amenazas y defensas contra amenazas m谩s significativas del oponente, lo que lleva a un resultado positivo para el jugador. Las combinaciones son atacantes (o ganadoras) y defensivas.
La combinaci贸n de ataque o victoria es exitosa si, en cualquier movimiento defensivo o de ataque del oponente, se encontraron movimientos de respuesta que conducen a una victoria. La combinaci贸n de ataque termina con la instalaci贸n de un tap贸n, que el oponente no puede cerrar.
La combinaci贸n defensiva, por el contrario, tiene 茅xito cuando el oponente deja de crear amenazas, o se excede el l铆mite de movimientos para el c谩lculo. Una combinaci贸n defensiva consiste en movimientos defensivos o crear una mayor amenaza para el oponente.
Al evaluar una posici贸n, se realiza una b煤squeda de una combinaci贸n ganadora. Si tiene 茅xito, ganamos. De lo contrario, si no hay amenazas del oponente, el estado es neutral. Si hay amenazas del oponente, buscamos una combinaci贸n defensiva. Si tiene 茅xito, el estado es neutral; si falla, perdemos.
Dado que el n煤mero de opciones para atacar y movimientos de represalia forzados es bastante limitado, est谩 permitido buscar combinaciones a una profundidad suficientemente grande. Durante la construcci贸n inicial de la estrategia 贸ptima, la profundidad permitida de la b煤squeda de combinaciones se estableci贸 en 25 movimientos. Al volver a calcular la soluci贸n para implementar el algoritmo de estimaci贸n de posici贸n en JavaScript, la profundidad de b煤squeda permitida se redujo a 17 movimientos.
Al calcular la estrategia 贸ptima, la profundidad de b煤squeda de la combinaci贸n ganadora desde arriba estaba limitada adicionalmente por el n煤mero m谩ximo de movimientos objetivo.
Estamos buscando una solucion
Entonces, calificamos la posici贸n dada como neutral y elegimos cu谩l ser谩 el pr贸ximo movimiento. Nuestro comportamiento en este caso depende de si somos el lado atacante o defensor. Para el lado atacante, la soluci贸n completa ser谩 una secuencia de movimientos en los que, para el movimiento de retorno de cualquier oponente, la posici贸n se eval煤a como ganadora (se encuentra una combinaci贸n ganadora) o contiene el siguiente movimiento propio en la soluci贸n. Vale la pena se帽alar que para calcular la estrategia 贸ptima, el lado atacante siempre es negro, el lado defensor es blanco.
El lado atacante necesita encontrar un solo movimiento, lo que lleva a la victoria m谩s r谩pida. En las condiciones de falta de recursos, el atacante limita artificialmente el n煤mero de opciones para atravesar, primero estudio los movimientos que conducen a la posici贸n con la puntuaci贸n m谩s alta. Despu茅s de encontrar cualquier soluci贸n, en la direcci贸n de la m谩s larga de ellas, el atacante ampl铆a el rango de opciones, explorando posiciones menos valoradas para reducir la duraci贸n de la soluci贸n.
Es suficiente que el lado defensor encuentre un solo movimiento que no conduzca a la victoria del oponente en el l铆mite de movimientos dado. Todas las celdas libres se pueden usar para la enumeraci贸n.
Para reducir la cantidad de movimientos que se ordenar谩n, utilizamos el algoritmo de "omisi贸n". Nos saltamos el movimiento defensivo y buscamos una combinaci贸n de ataque ganadora. Si tiene 茅xito, los posibles movimientos de defensa pueden limitarse a los movimientos que afectan el 茅xito de la combinaci贸n encontrada. En promedio, en cada paso esto le permite reducir el 谩rea de b煤squeda de 4 a 6 veces. Tenga en cuenta que entre los movimientos ignorados puede haber ramas m谩s largas de la soluci贸n. Por lo tanto, para buscar soluciones 贸ptimas, el algoritmo de "omisi贸n" se usa solo en la b煤squeda inicial.
Calculamos la estrategia
Todos los componentes est谩n listos, colocamos la primera piedra negra en el centro del campo, comenzamos la b煤squeda de una soluci贸n y ... En esto, despu茅s de unas horas, los recursos de mi computadora port谩til se agotan y tengo que admitir la derrota "en batalla, pero no en batalla".
En verdad, ten铆a a mi alcance la potencia de c谩lculo con Xeon de un n煤cleo y medio y un terabyte de RAM libre. Pero, recuerde que a mediados de los noventa, Allis solo ten铆a 10 SUN SPARCstation 2 en cada uno de 128 MB de RAM, sinti贸 remordimiento por el comportamiento antideportivo y decidi贸 limitar la cantidad de RAM en la m谩quina Java a 1 GB y asign贸 solo 1 hilo para la tarea El procesador. De alguna manera podr铆a compensar mis GHz en comparaci贸n con sus MHz. Adem谩s, se prometi贸 al final del trabajo transferir los algoritmos a JavaScript para el navegador.
Entonces, la b煤squeda de estrategias tuvo que comenzar con la decisi贸n de los bocetos de debut. Una descripci贸n detallada de los debuts para el juego de Renju en ruso se puede encontrar en los famosos libros de Sagar "From Debut to Middlegame" y "Ringing of the Stones" de Mikhail Kozhin y Alexander Nosovsky. Los libros ya tienen 20 a帽os, pero desde entonces se ha publicado un poco de dicha literatura. La colecci贸n m谩s reciente de Dmitry Epifanov "Tigre en una jaula" de 2015, lamentablemente, no est谩 disponible en formato electr贸nico.
La b煤squeda de decisiones de apertura 贸ptimas se llev贸 a cabo de acuerdo con el siguiente algoritmo. En el primer paso, se realiz贸 un c谩lculo preliminar sin limitar la longitud del lote. Luego, para las soluciones m谩s largas, se realiz贸 la optimizaci贸n: reemplazando las combinaciones encontradas con soluciones m谩s cortas para los pasos finales y buscando ramas de decisi贸n m谩s cortas para todos los movimientos intermedios. La optimizaci贸n se realiz贸 hasta que se alcanz贸 el l铆mite objetivo para todas las ramas de la soluci贸n. Luego, el l铆mite objetivo disminuy贸 y se intent贸 optimizar a un nuevo valor.
No hubo problemas con el tercer debut vertical en la Figura 3. El resultado fue un conjunto completo de soluciones. Como resultado, las posiciones m谩s dif铆ciles despu茅s del cuarto movimiento i8 y j10 se resolvieron en 31 movimientos. Luego se estableci贸 un l铆mite objetivo de 35 movimientos por juego.
Desde la diagonal para la decisi贸n, tradicionalmente eligi贸 el s茅ptimo debut. La posici贸n m谩s dif铆cil surge despu茅s del cuarto movimiento g9. Se encontraron soluciones de longitud permisible para 6 movimientos g8 y g7.
Pero para esta opci贸n, con el sexto movimiento en j9, no pude encontrar una soluci贸n m谩s corta que 33 movimientos. Fue casi un desastre. Por desesperaci贸n, prob茅 las soluciones para el quinto movimiento alternativo, as铆 como todos los otros tipos de aberturas diagonales. Los debuts se resolvieron hasta el final, pero no se pudo encontrar nada m谩s corto que 39 movimientos por juego.
Volviendo al debut de la s茅ptima diagonal original, rehizo el algoritmo para generar oraciones para movimientos de ataque. Como resultado, los movimientos que conducen a posiciones con un puntaje de calificaci贸n de los terceros diez inesperadamente comenzaron a dar un resultado y reducir la longitud del camino de la soluci贸n. La variabilidad del c谩lculo con tal cantidad se hizo bastante grande. Con una profundidad de soluci贸n de 12 movimientos, hab铆a m谩s de 2 millones de posiciones (excluyendo posiciones cuando se buscaban combinaciones). La continuaci贸n se bas贸 en 1 GB de RAM asignada para la tarea. Por lo tanto, para verificar la decisi贸n hasta la bifurcaci贸n final, en algunos casos fue necesario decidir por separado las posiciones del movimiento 18.
Despu茅s de que se decidiera el s茅ptimo debut diagonal en 35 movimientos dados, se pod铆a celebrar la victoria: se gan贸 la lucha por el centro. A煤n quedaba una enorme cantidad de trabajo computacional de rutina, c谩lculos de movimientos blancos "no 贸ptimos" para completar la estrategia. Del volumen total de la estrategia 贸ptima, la respuesta a tales movimientos como resultado fue del 80%. Afortunadamente, se resolvieron autom谩ticamente por completo en el c谩lculo preliminar despu茅s del segundo movimiento, y todo este volumen se agreg贸 a la estrategia 贸ptima en un par de d铆as.
Entonces, se encontraron soluciones para los 2 movimientos. Ponemos la primera piedra negra en el centro del campo, comenzamos la b煤squeda de una soluci贸n y ni siquiera tenemos tiempo para sentir la importancia del momento: la posici贸n inicial se resolvi贸 en 35 movimientos. Se construye el gr谩fico de la estrategia ganadora 贸ptima.
Comprob谩ndonos a nosotros mismos
El siguiente paso es verificar la soluci贸n. Apague la inteligencia del lado defensor por completo. Despu茅s de cada movimiento de las negras, las blancas van a cualquier casilla libre del tablero. La posici贸n obtenida despu茅s del movimiento de las Blancas debe encontrarse en el gr谩fico de decisi贸n o evaluarse como ganadora por el n煤mero de movimientos que no exceden la rama m谩s larga en la posici贸n inicial. Al evaluar cada posici贸n, verificamos la combinaci贸n ganadora encontrada para todos los movimientos admisibles de las blancas antes de que las negras construyan la pieza final, cinco seguidas.
La verificaci贸n se realiz贸 varias veces hasta completarse. La ejecuci贸n final sin errores en modo de subproceso 煤nico tard贸 14 horas. En el curso de la verificaci贸n, se encontraron y corrigieron errores que surgieron como resultado de diferencias en la profundidad de b煤squeda de combinaciones, suposiciones para omitir, duplicaci贸n de posiciones sim茅tricas.
Responda la pregunta: 驴la decisi贸n en 35 movimientos es realmente la m谩s 贸ptima? Seg煤n mi investigaci贸n, para varias de las ramas m谩s largas del debut vertical, es posible encontrar soluciones m谩s 贸ptimas con una longitud de 33 movimientos. Pero para la diagonal despu茅s del sexto movimiento en j9, se dedic贸 mucho tiempo a buscar una soluci贸n en 33 movimientos, la variaci贸n para las negras se expandi贸 a 50 movimientos en cada paso y fue en vano. No es posible demostrar rigurosamente la falta de una soluci贸n en 33 movimientos, el tiempo asignado para el proyecto ha llegado a su fin y se tom贸 la decisi贸n de detenerse en el l铆mite objetivo de 35 movimientos.
Convertir de java a javascript
La publicaci贸n de una soluci贸n a un problema requiere claridad.
Para usar la soluci贸n directamente en el navegador, se requer铆a:- Reduce la profundidad de la b煤squeda de combinaciones al evaluar posiciones a 17 movimientos. Esto condujo a un aumento de 2-3 veces en el n煤mero de movimientos calculados de la estrategia 贸ptima.
- Convierta el formato de gr谩fico de decisi贸n binario a la secuencia JSON de movimientos. Este formato es m谩s conveniente en JavaScript y visual.
- Convierta clases java a m贸dulos javascript, excepto para los procedimientos de toma de decisiones. Aqu铆, en la interfaz web, reemplace las llamadas de servicio de descanso con funciones locales.
Lista de clases de aplicaci贸n:- Junta - gesti贸n de fiestas en la junta, interfaz visual
- V茅rtice : parte superior del gr谩fico de decisi贸n, heredado de la posici贸n
- Borde - borde del gr谩fico de decisi贸n, mover posiciones de conexi贸n
- Dise帽o : posici贸n, contiene una colecci贸n de l铆neas
- L铆nea : una l铆nea en una direcci贸n determinada, contiene una colecci贸n de formas
- Figura : una figura que determina el tipo y el inicio de una figura en una l铆nea
- Patr贸n : patrones de figuras para comparar al buscar
La soluci贸n completa en formato JSON se puede descargar del archivo gomoku.json .Fuentes en el repositorio en GitHub .Para mayor claridad, dar茅 a continuaci贸n ejemplos de los juegos m谩s largos obtenidos en la demostraci贸n haciendo clic en Siguiente.Debut diagonal:
Debut vertical:
