Niveles de dificultad de lectura
Introducción y reglas del juego.
Hace unos años compré el juego Dobble ( Dobble , el nombre original es "Spot It!"). Este es un juego muy simple, rápido y divertido, que considero uno de los mejores juegos de mesa en general.
Hay 55 cartas en el juego con 8 símbolos diferentes en cada una. Así se ven estas tarjetas:

Fig. 1. Un ejemplo de una tarjeta de juego.
En cada dos cartas, uno y solo un símbolo coincide. En la figura anterior, este es un símbolo de lápiz:

Fig. 2. Caracteres coincidentes en tarjetas.
El jugador que vio por primera vez el partido realiza una acción en una de las cartas, dependiendo de la ronda del juego. Por ejemplo, se lo lleva a sí mismo o se lo arroja a un oponente.
A menudo, esto lleva al hecho de que una de las cartas para las que los jugadores buscan partidos está cambiando. Debido a esto, debe buscar una nueva coincidencia, que puede ser un símbolo completamente diferente:


Fig. 3, 4. La primera tarjeta se reemplaza por una nueva. Ahora hay una nueva coincidencia entre ellos: el símbolo del payaso.
Como lo hacen
A primera vista, parece increíble que en dos tarjetas exactamente una coincidencia, ni más ni menos. Las preguntas surgen de inmediato: ¿cuántos personajes hay en el juego? No pueden ser muy pocos (entonces habrá más de un partido en las cartas) o demasiado (entonces puede que no haya ningún partido en las cartas).
Además, es obvio que los símbolos se encuentran en las tarjetas en un orden especial, lo que garantiza la única coincidencia para dos tarjetas.
Las habilidades elementales de Google nos llevan al sitio web stackoverflow, que describe por qué sucede esto: http://stackoverflow.com/questions/6240113/what-are-the-mathematical-computational-principles-behind-this-game
El juego usa los principios de la geometría finita . Aunque existe la palabra "geometría" en esta frase, este concepto se refiere más a la combinatoria que a la geometría. Opera con un número finito de puntos que pueden ubicarse, en particular, en forma de un plano proyectivo .
Las cartas y los símbolos en el juego son elementos del plano proyectivo del séptimo orden. Esto significa que en cada carta hay un símbolo n + 1 , y el número total de símbolos únicos en el juego es n ^ 2 + n + 1 , es decir 57 caracteres.
Hay planos de orden inferior y superior. Por ejemplo, hay un plano de quinto orden. Para ella, se muestran 6 símbolos en la tarjeta, y el número total de símbolos únicos en el juego es 5 ^ 2 + 5 + 1 = 31. El plano proyectivo de esta configuración se usa en una versión más simple del juego Doble llamada "Doble 1,2,3" .
La conexión entre puntos y líneas para el plano proyectivo se establece utilizando la matriz de incidencia . Su aparición se presenta en la sección "Matriz de incidencias para el juego Dobble".
Geometría final para bebes
Mucho más tarde que escribir el artículo original, asistí a una conferencia de Alexei Savvateev , donde habló sobre geometría proyectiva mucho más corta y más comprensible. Pero debido a que no tengo la fuerza o el deseo de volver a escribir la mitad del artículo debido a esto, solo recomiendo su libro "Matemáticas para las Humanidades", si mi intento por parte del salvaje de explicar el dispositivo del automóvil con los dedos fuera incomprensible o aburrido.
Primero, vaya a Wikipedia y lea algunos artículos. El primer artículo describe el concepto de geometría finita:
Una geometría finita es cualquier sistema geométrico que tiene un número finito de puntos . [1]
Hasta ahora, todo es simple. Si dibuja varios puntos con un bolígrafo sobre papel, entonces ya formarán algún tipo de geometría finita.
Una sorpresa espera a muchos más:
Por ejemplo, la geometría euclidiana no es finita, porque la línea euclidiana contiene un número ilimitado de puntos, o más bien, contiene exactamente tantos puntos como números reales . [1]
Para nosotros, esto significa que el trozo de papel en el que se dibujan nuestros puntos no es un plano en términos de geometría finita . Es solo un portador de puntos.
Hay dos tipos de geometría en el plano: afines y proyectivos . En geometría afín, se utiliza la noción habitual de paralelismo de líneas. [1]
Recordemos qué axiomas describen la geometría afín:
La geometría afinada en un plano es un conjunto no vacío X (cuyos elementos se llaman "puntos"), con una colección no vacía de L subconjuntos de X (cuyos elementos se llaman "directos"), de modo que:
- Para dos puntos diferentes, solo hay una línea que contiene ambos puntos.
- Para una línea ℓ y un punto p que no pertenece a ℓ , existe una y solo una línea ℓ ′ que contiene p tal que ℓ ∩ ℓ ′ = ∅.
- Hay muchos de cuatro puntos, ninguno de los cuales se encuentra en la misma línea. [1]
Estos axiomas nos dan la oportunidad de comprender cómo se ve el plano afín más simple en geometría finita:
El plano afín más simple contiene solo 4 puntos y se llama plano afín de segundo orden . Cada par de puntos define una línea única, por lo tanto, el plano indicado contiene 6 líneas. [1]
¿No está muy claro? Eso es correcto Si observa detenidamente la definición de geometría afín, puede ver que funciona con los conceptos de teoría de conjuntos (elemento, conjunto, subconjunto).
Esto significa que las líneas pueden no parecerse a las líneas habituales de la geometría euclidiana.
De hecho lo es. Si observa la imagen del avión afín de segundo orden, veremos la siguiente imagen:

Fig. 5. Plano ateniense de segundo orden. (Fuente ru.wikipedia.org )
Los puntos aquí parecen puntos negros ordinarios, pero las líneas rectas son segmentos multicolores. Las líneas del mismo color se consideran paralelas.
Como puede ver, las líneas aquí no son de longitud infinita. En secreto, diré que no hay ningún concepto de longitud aquí en absoluto, y las líneas rectas pueden tener cualquier forma, como veremos pronto.
Seguramente% username% aún duda de que la imagen de este plano satisfaga los axiomas de la geometría afín. Vamos a ver:
- Tomamos 2 puntos, por ejemplo, la parte superior izquierda y la inferior izquierda.
Ambos puntos contienen solo una línea roja izquierda.
La línea roja derecha no contiene ninguno de estos puntos, y las líneas restantes contienen solo uno de ellos. - Tome la línea recta roja izquierda y el punto superior derecho. Obviamente, solo una línea recta (rojo derecho) es paralela a la línea roja izquierda, ya que pasa por el punto superior derecho, pero no pasa por ninguno de los dos puntos izquierdos.
- La figura muestra claramente que no importa los 3 puntos que tomemos, uno de ellos se encuentra en una línea diferente de la línea en la que se encuentran los otros dos puntos.
Las dos líneas que forman las diagonales de un cuadrado no se cruzan, ya que no tienen puntos comunes.
Si entendió bien el contenido de la imagen anterior, entonces la imagen es más complicada:
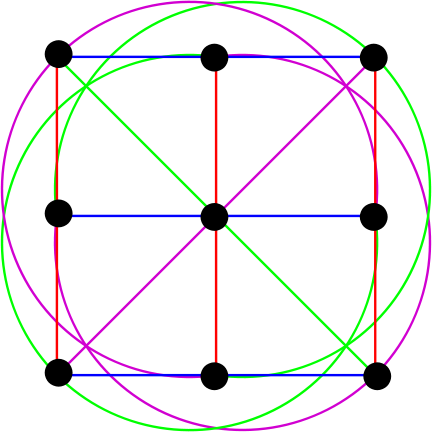
Fig. 6. Plano ateniense de tercer orden. (Fuente ru.wikipedia.org )
Aquí vemos 9 puntos y 12 líneas. Sí,% username%, estas elipses son en realidad líneas rectas en términos de geometría finita.
Las formas del mismo color son líneas paralelas. Son difíciles de notar, por lo que dividimos la imagen en varias:
| Plano número 1 | Plano número 2 | Plano número 3 | Plano número 4 |
|---|
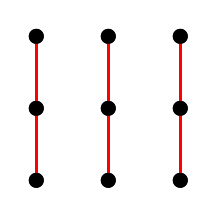 | 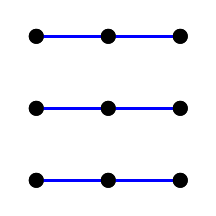 |  |  |
Fig. 7. Líneas rectas paralelas del plano afín de tercer orden.
Aquí, verificar la ejecución de los axiomas llevará un poco más de tiempo:
- Tomamos 2 puntos, por ejemplo, el centro superior e inferior derecho. A través de ellos pasa solo una de las líneas moradas.
- Tome la línea roja izquierda y el punto inferior derecho. De manera similar a un plano de segundo orden, solo una línea roja derecha pasa por este punto, pero no pasa por ninguno de los tres puntos izquierdos.
- Aquí es un poco más complicado que en el caso de un avión de segundo orden. La declaración del axioma dice que necesita encontrar al menos un conjunto (no vacío) de cuatro puntos, en el que no hay tres en más de una línea.
Obviamente, 12 juegos con tres puntos a través de los cuales pasan las líneas en la figura no satisfacen esta condición. Pero satisface, por ejemplo, un conjunto de cuatro puntos de esquina.
En un caso más general, un plano afín finito de orden n tiene n ^ 2 puntos y n ^ 2 + n líneas; cada línea contiene n puntos, y cada punto pertenece a n + 1 líneas. [1]
Con la geometría afinada terminada, pasamos al segundo tipo de geometría en el plano: proyectiva.
En geometría proyectiva, por el contrario, cualquiera de las dos líneas se cruzan en el único punto posible y, por lo tanto, no existen líneas paralelas. [1]
La oración anterior describe el segundo axioma de la geometría proyectiva. El primero y el tercero son los mismos que en el ateniense.
Dado que el tercer axioma requiere la existencia de al menos cuatro puntos, el plano debe contener al menos 7 puntos para satisfacer las condiciones de los dos primeros axiomas. En este plano proyectivo más simple también hay 7 líneas; cada punto pertenece a tres líneas y cada línea contiene tres puntos. Tal plano proyectivo a menudo se llama el "plano Fano" . [1]
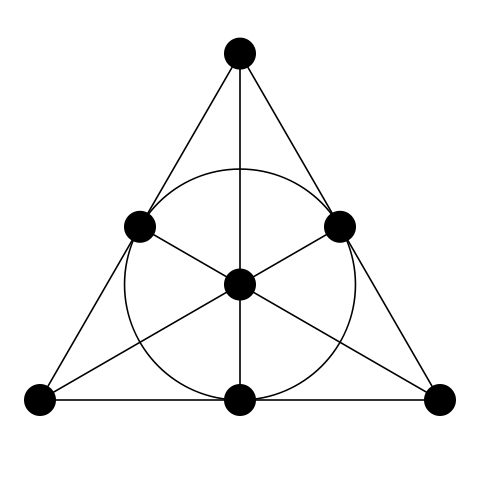
Fig. 8. Avión Fano. (Fuente en.wikipedia.org )
En esta figura, es difícil entender de inmediato las 7 líneas, así que aquí hay una versión en pony del mismo plano:
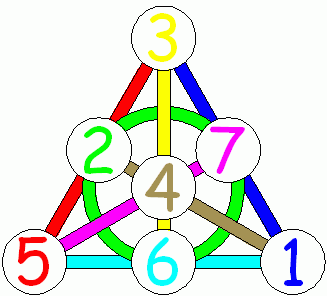
Fig. 9. Avión Fano con líneas de colores. (Fuente mathpuzzle.com . Usado con permiso de Ed Pegg Jr. )
Entonces, el plano Fano es un plano proyectivo de 2 órdenes con 7 puntos y 7 líneas.
¿Qué tiene que ver la tarjeta con ella?
¿Qué sucede si reformulamos 2 axiomas de geometría finita , reemplazando la "línea" con el "símbolo" y el "punto" con la "tarjeta"?
El resultado es este:
- Para dos cartas diferentes, solo hay un símbolo, que se muestra en ambas cartas.
- Para dos símbolos diferentes, solo hay una tarjeta que contiene ambos símbolos.
Ahora, en base a este conocimiento, veamos cómo se vería Dobble en el caso más simple. Tendría 7 cartas y 7 caracteres, cada carta tendría 3 caracteres (ya que 3 líneas se cruzan en un punto):
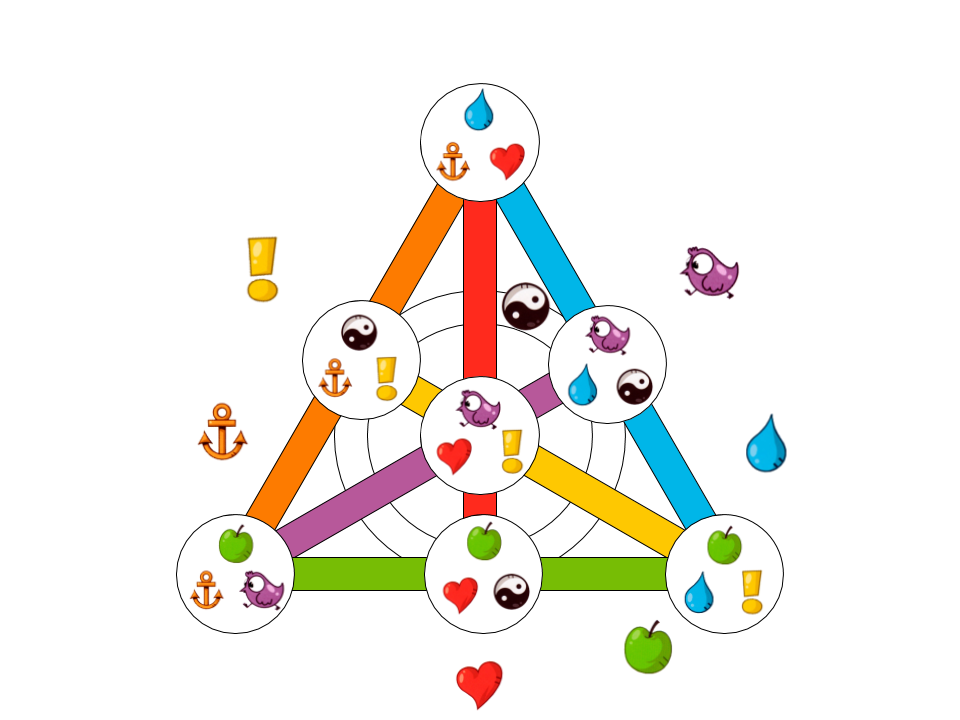
Fig. 10. Un ejemplo del juego de cartas más pequeño posible para Dobble.
Aquí se usan los siguientes 7 caracteres:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
No importa qué 2 cartas tomemos, tendrán un símbolo común, representado al lado de la línea en la que se encuentran ambas cartas.
Por ejemplo, la tarjeta en la esquina inferior izquierda y la tarjeta en el medio del lado derecho tienen un símbolo común  . Se muestra al lado de la línea.
. Se muestra al lado de la línea.  .
.
Planos proyectivos de pequeños pedidos.
En Wolfram puede encontrar una demostración visual de planos proyectivos de pedidos pequeños: http://demonstrations.wolfram.com/ProjectivePlanesOfLowOrder/
Está diseñado como un documento en el formato CDF (Formato de documento computable), para el cual necesita instalar el Reproductor CDF .
Aquí hay un ejemplo de un plano proyectivo de orden 3:
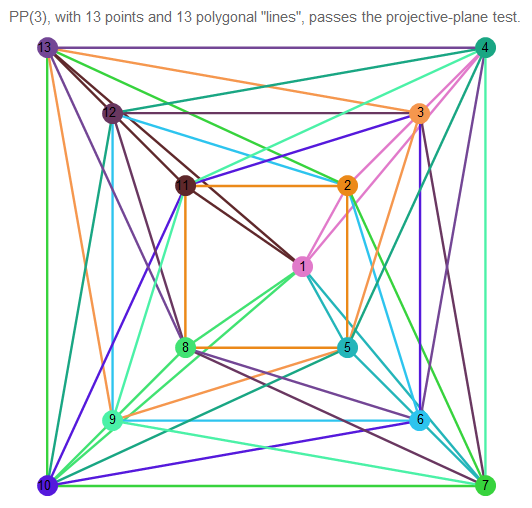
Fig. 11. Imagen del plano proyectivo de 3 órdenes.
Es difícil entender lo que está sucediendo, así que tome 2 líneas arbitrarias:
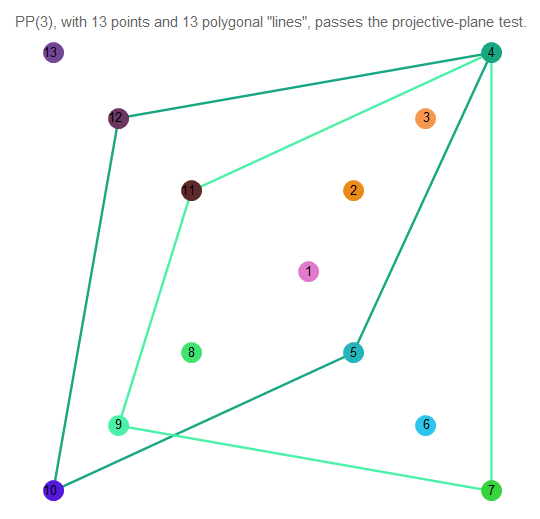
Fig. 12. La intersección de dos líneas del plano proyectivo de tercer orden.
Como vemos, se cruzan exactamente en un punto. Las líneas en sí contienen 4 puntos.
Para asegurarse de que 4 líneas pasan a través de cada punto, debe cambiar los pares de líneas que se muestran en un documento interactivo y centrarse en algún punto.
Los planos proyectivos de órdenes superiores se muestran en las siguientes figuras.
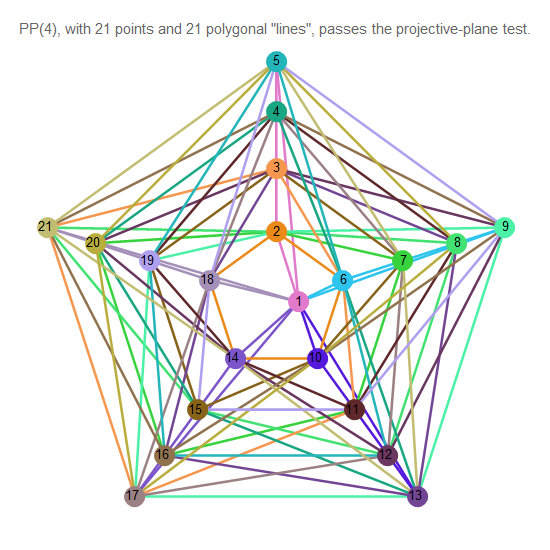
Fig. 13. Plano proyectivo de orden 4
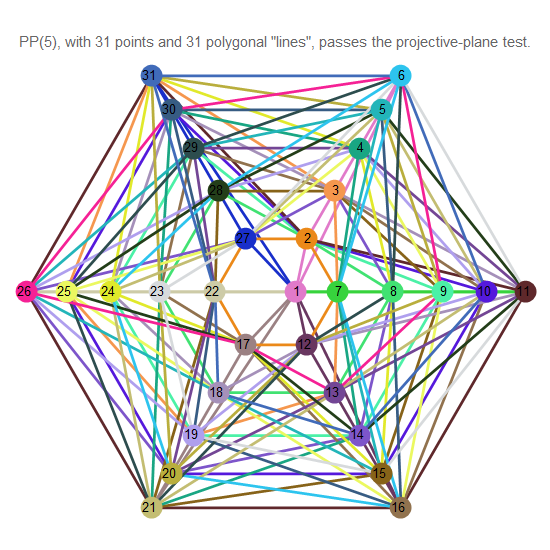
Fig. 14. El plano proyectivo de orden 5

Fig. 15. Plano proyectivo de orden 7
En la secuencia anterior, no hay imagen para el plano proyectivo del sexto orden. Esto no es un error.
Aunque Wolfram genera una representación gráfica de dicha estructura, no satisface los axiomas de la geometría proyectiva y no es un plano proyectivo.
Se supone, pero aún no se ha probado, que el orden de un plano finito es siempre una potencia primordial . [1]
¿Cómo construir un plano proyectivo?
La representación gráfica del plano proyectivo parece interesante y clara, pero ¿cómo encontrar esa combinación de puntos para que posea las propiedades anteriores?
La forma más fácil es visitando sitios que alojan datos precalculados para planos proyectivos de varios pedidos.
Por ejemplo, para el plano proyectivo de orden 7, puede visitar la siguiente página: https://web.archive.org/web/20170619110638/https://www.uwyo.edu/moorhouse/pub/planes/pg27.txt
Allí se presenta una matriz de números. Las líneas son cartas (puntos) en términos de Dobble. Los números en las líneas son los números de serie de los caracteres (líneas), comenzando desde cero, que se dibujan en cada tarjeta (pasan por este punto).
También puede usar los servicios de paquetes matemáticos, como Matlab, para construir la matriz de incidencia del plano proyectivo. [2] [3]
Matrices de incidencia
La matriz de incidencia es una de las representaciones del gráfico que indica las relaciones entre los elementos incidentes del gráfico (borde (arco) y vértice). Las columnas de la matriz corresponden a aristas, las filas a vértices. Un valor distinto de cero en la celda de la matriz indica la relación entre el vértice y el borde (su incidencia ). [2]
Uno de los ejemplos más simples de la matriz de incidencia puede ser una matriz de 2x1 para un gráfico no dirigido de dos vértices conectados por un borde:

Fig. 16. Un gráfico no dirigido de dos vértices conectados por un borde, y su matriz de incidencia.
Un ejemplo más complejo de un gráfico y su matriz de incidencia:
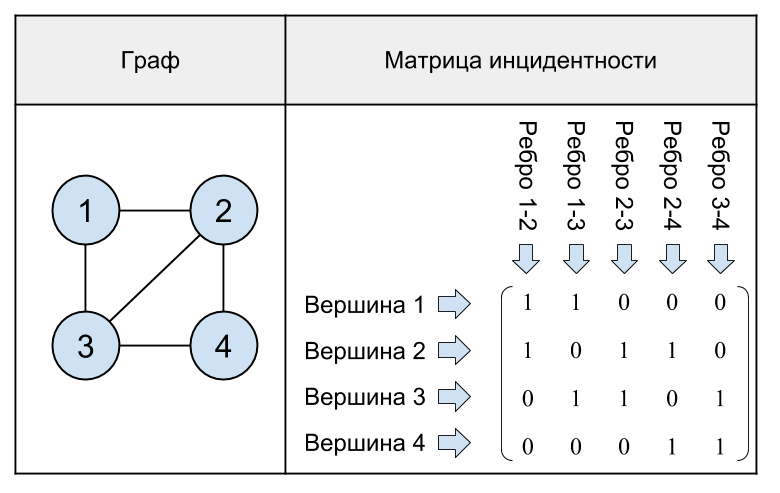
Fig. 17. Un gráfico no dirigido con 4 vértices y su matriz de incidencia.
Como se puede ver en el último ejemplo, en la matriz de incidencia del gráfico en cada columna hay exactamente dos unidades, porque un borde conecta dos vértices.
El plano proyectivo es una hipergrafía , ya que una línea (borde) conecta varios puntos (vértices). Por lo tanto, en la matriz de incidencia del plano proyectivo, las unidades en cada columna ocurren n + 1 veces, donde n es el orden del plano proyectivo.
Para el avión Fano que se muestra en la Fig. 9, la matriz de incidencia será la siguiente:

Fig. 18. La matriz de incidencia del plano de Fano.
Para simplificar la percepción, los ceros no se muestran y las unidades se reemplazan por el símbolo X.
En esta representación del plano proyectivo, el principio de dualidad de puntos y líneas es claramente visible: la línea atraviesa exactamente 3 puntos y, al mismo tiempo, el punto pertenece exactamente a tres líneas.
Construyendo un plano proyectivo por fuerza bruta
El conocimiento actual sobre las propiedades de la matriz de incidencia es suficiente para construirlo para el plano proyectivo de cualquier orden n. Para hacer esto, puede usar el siguiente pseudocódigo:
n+1 , n+1 , ,
Siguiendo este algoritmo, obtenemos una matriz simétrica para el plano Fano:

Fig. 19. La matriz de incidencia del plano de Fano construida por el algoritmo de pseudocódigo.
Esta matriz no coincide con la anterior. De hecho, no importa.
La permutación de cualquiera de las dos filas de la matriz de incidencia es equivalente a renumerar los vértices del gráfico.
La permutación de cualquiera de las dos columnas de la matriz de incidencia es equivalente a la renumeración de los bordes del gráfico (si están numerados de antemano).
Matriz de incidentes para Dobble
Para el juego Dobble en la matriz de incidencia, las filas son responsables de las cartas, y las columnas son responsables de los personajes en ellas.
Por lo tanto, la permutación de cualquiera de las dos columnas de la matriz de incidencia es equivalente a un cambio en la secuencia de caracteres en la tarjeta. Sin embargo, los símbolos en la tarjeta no están ordenados, por lo que esta operación no afecta la apariencia de las tarjetas.
La reorganización de dos líneas significa que en todas las tarjetas dos símbolos correspondientes se reemplazan entre sí.
La última operación cambia la apariencia de las cartas, lo que significa que el conjunto de personajes que vemos en el juego es solo una de las combinaciones posibles.
El número de juegos de caracteres para una carta dada es una combinación de 57 elementos y 8 elementos sin repetición. Se calcula mediante la fórmula. 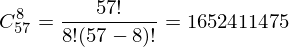
La matriz de incidencia para Dobble se muestra en la tabla a continuación. Se transpone, es decir las filas son símbolos y las columnas son tarjetas (se puede hacer clic en la imagen). Habr no le permite insertar una imagen del tamaño y la calidad deseados, por lo que la opción de tamaño completo es un enlace separado: https://github.com/Skybladev2/DobbleMathModel/blob/master/images/Dobble%20incidence%20matrix.png

Fig. 20. La matriz de incidencia del juego Dobble.
¿Qué dos cartas faltan en el juego?
En total, la tabla con la matriz de incidencia del juego tiene 57 filas y 55 columnas. Esto significa que el juego podría tener 2 cartas más.
Esto significa que los personajes que deberían estar en estas cartas son menos comunes en el juego que el resto. El número de personajes en el juego se muestra en la última columna de la tabla.
El número de personajes de las cartas que faltan es el siguiente:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  y
y 
(14 caracteres en total) ocurren 7 veces. ocurre 6 veces
ocurre 6 veces
¿Cómo son las cartas que faltan? Para responder a esta pregunta, tome cualquiera de los caracteres anteriores en la matriz de incidencia (excepto el muñeco de nieve) y colóquelo en la tarjeta que falta (por ejemplo, la penúltima columna).
Luego encontramos todas las cartas (columnas) en las que se representa este símbolo. Esto significa que en todas estas cartas los símbolos coinciden, y no puede haber otras coincidencias.
Dado que estas cartas ya tienen una coincidencia con el personaje seleccionado, tache de la penúltima columna todos los personajes que aparecen en las otras cartas.
Faltan personajes que no han sido tachados, y forman los personajes de una de las cartas restantes. Como resultaron ser exactamente 8, el tipo de la segunda carta que falta se determina sin ambigüedades.
Aquí están estas 2 cartas:


Fig. 21. Un posible tipo de cartas faltantes es el No. 56 y el No. 57.
Queda por responder la última pregunta: ¿la ausencia de estas cartas afecta la propiedad de la coincidencia de un solo símbolo entre dos cartas (es decir, de repente no hay coincidencias entre las cartas)?
La respuesta es obvia, si aún observa la matriz de incidencia del juego, no, no lo hace. Entre dos cartas (columnas) sigue siendo la única coincidencia.
¿Por qué hay 2 cartas menos que el máximo posible en el juego?
Inicialmente, las reglas para los cinco minijuegos no estaban en el folleto, sino en cinco cartas separadas. Al mismo tiempo, solo se pueden imprimir 60 tarjetas. Por lo tanto, los autores del juego decidieron eliminar 2 cartas, por lo que al final resultaron 55 cartas con símbolos + 5 cartas con reglas. (Un agradecimiento especial a Guillaume Gille-Naves por su aclaración).
Agradecimientos
Expreso mi gratitud a la red de tiendas de juegos de mesa "Igroved" por su ayuda en la redacción del artículo.
Gracias a Ed Pegg Jr por proporcionar la imagen del avión Fano.
Por separado, quiero mencionar un anónimo y un Maestro para que me ayuden a revisar el artículo.
Agradezco a la tienda "Table City" por su ayuda en la preparación para la publicación del artículo.
De todo corazón agradezco a los autores del juego Igor Polouchine, Denis Blanchot, Guillaume Gille-Naves, así como a Asmodee por el derecho a usar imágenes del juego.