Ternario equilibrado
Estoy trabajando en una conferencia sobre principios de arquitectura de computadoras para nuestra universidad; y como tarea, me gustaría proponer a mis alumnos que construyan una máquina programable simple que funcione en
ternary . La razón principal es divertida: como profesor debo traer un poco de entretenimiento, de lo contrario no me escucharán. Además, es importante por razones históricas. ¿Algún "por qué?" las preguntas serán respondidas "Porque puedo".
Esta página describe los conceptos básicos, no irá más allá de un simple sumador ternario (y su implementación de hardware). Estén atentos para más.
Elegí el sistema ternario equilibrado: cada trit representa uno de los tres estados posibles, -1, 0 o 1. Una descripción muy extensa de este sistema se puede encontrar
aquí .

El bloque de construcción básico: multiplexor ternario
Abstracción
El único bloque que se usará en mi computadora es el multiplexor ternario.
Se puede ver como una caja negra con cinco pines: el pin selector recibe una señal ternaria (-1, 0 o 1), y luego hay un pequeño interruptor dentro de la caja que conecta el pin de salida con uno de los tres pines de entrada inN, inO o inP.
Por lo general, se representa como se muestra aquí:
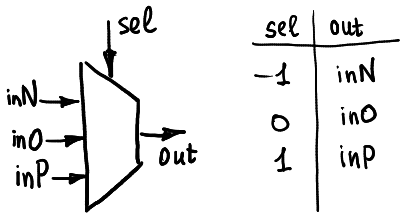
El demultiplexor ternario funciona de manera similar: dependiendo del pin selector, una entrada está conectada con uno de los tres pines de salida posibles. Tenga en cuenta que en mi hardware utilizo interruptores analógicos CMOS. Esos son bidireccionales, por lo que el hardware se puede usar tanto como multiplexor como demultiplexor. Pero de todos modos, por ahora no uso las posibilidades de demultiplexación.
Implementación de hardware
El diseño básico fue propuesto por
Shaos .
Lo único que hice fue crear la versión SMD de TRIMUX. Los interruptores dg403 de montaje en superficie se pueden comprar por 50p por pieza en China.
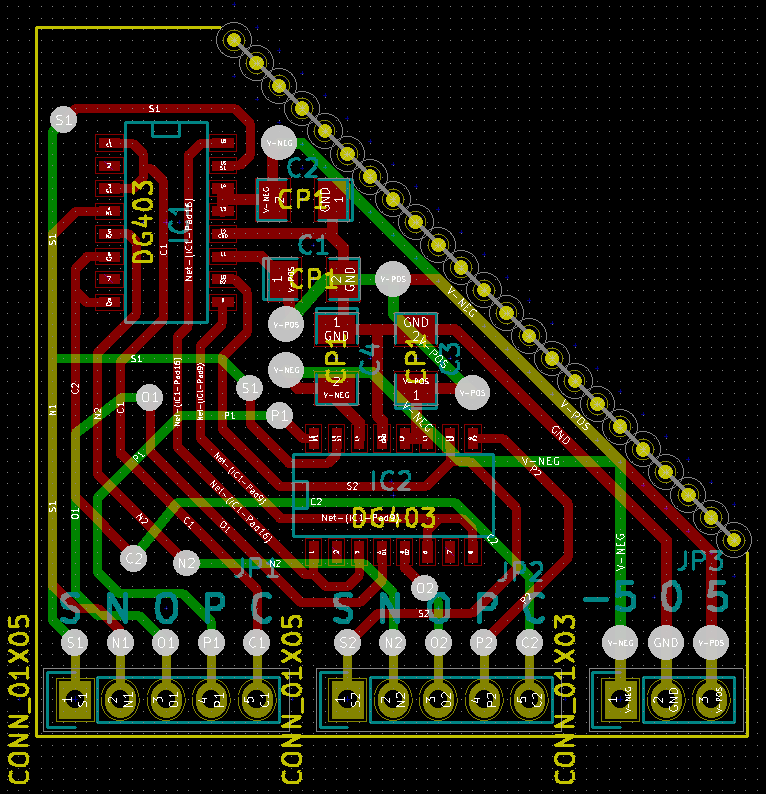
Antes de encontrar este diseño, intenté usar combinaciones de cd4007 y cd4016. Funcionó, pero el hardware es engorroso y feo. Los conmutadores DG403 brindan verdaderas posibilidades de computación ternaria sin redundancia, como usar binarios de dos bits y prohibir una de las cuatro configuraciones.
Se puede crear un multiplexor ternario con dos DG403: uno de los circuitos integrados recibe una entrada de potencia de -5V a 0V, mientras que el otro se alimenta con 0V a 5V, y permite utilizar señales ternarias representadas por tres tensiones -5V, 0V y 5V, respectivamente. Este diseño usa solo la mitad de los pines dg403, por lo tanto, es natural crear una placa con dos multiplexores.
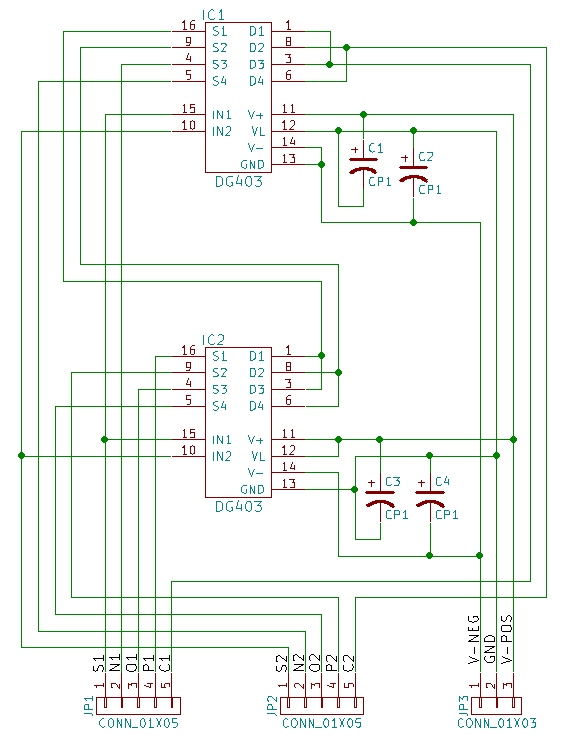
No dudes en contactar a Shaos
aquí . ¡Increíble, en lugar de especular sobre los beneficios del ternario, diseñó y fabricó sus propios circuitos integrados ternarios!

¿Cómo usarlo? Funciones unarias
Omitamos la función de identidad que podemos obtener dando -1.0 y 1 a los pines de entrada correspondientes del multiplexor.
Para comenzar, incrementemos la señal de entrada A calculando A + 1 (por supuesto, en el anillo -1,0,1):
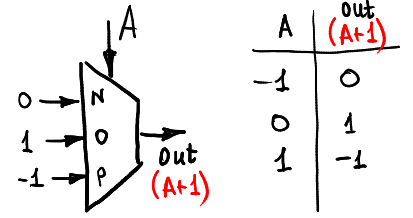
Aquí está la forma en que podemos disminuir la entrada:
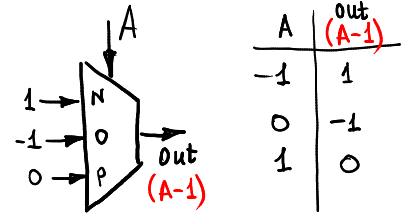
Calculemos max (A, 0):
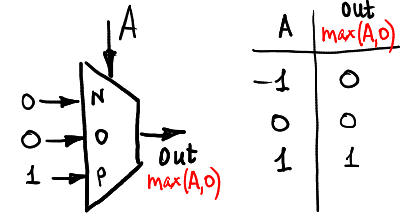
Y el mínimo (A, 0):
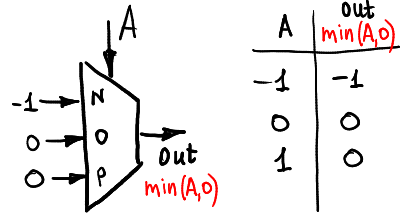
Funciones de dos argumentos: medio sumador
A + B
Entonces, un multiplexor nos permite calcular cualquier función unaria. Para calcular una función de dos argumentos necesitamos usar tres o cuatro multiplexores. Por ejemplo, si queremos calcular una suma de dos señales A y B (todavía en el anillo -1,0,1), entonces podemos usar este esquema:
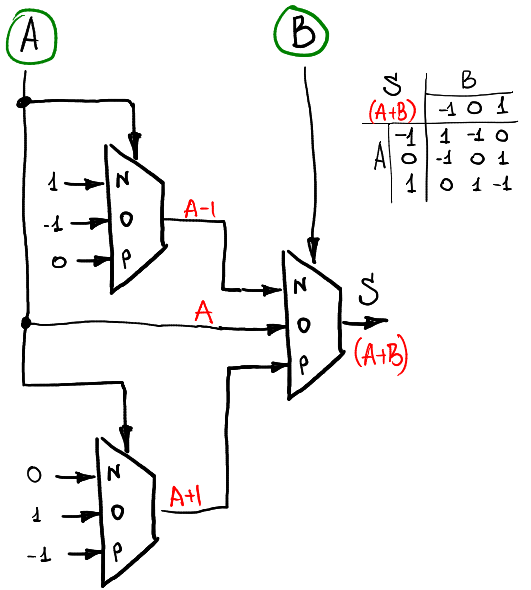
Hay dos capas de multiplexores: el primero calcula las funciones unarias de A, y la segunda capa las combina de acuerdo con B.
Consenso
Si queremos calcular la función de consenso de dos señales ternarias (el consenso es igual a -1 si A = B = -1, igual a 1 si A = B = 1 y, de lo contrario, es cero), entonces podemos hacerlo así:
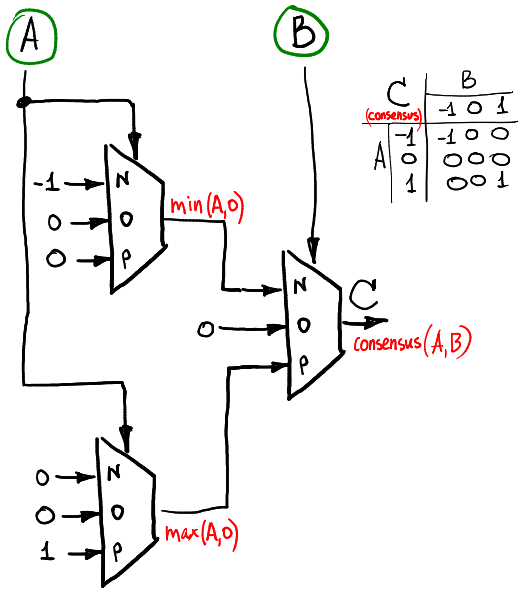
Implementación de hardware
De hecho, acabamos de crear
un medio sumador . Para dos entradas A y B, calcula dos salidas S y C relacionadas como A + B = S + 3 * C. S es la suma y C es la bandera de acarreo.
¡Probemos el diseño! El LED rojo significa -1, apagado significa 0, el LED verde significa 1. Por lo tanto, esta foto nos dice que S = -1, C = 1 o, en otras palabras, 1 + 1 = -1 + 3 * 1:

Aquí está la tabla que enumera los nueve estados posibles de nuestro medio sumador. Cada celda proporciona los valores correspondientes para S y C. Se proporciona un enlace a una foto para cada celda.
Tres argumentos: sumador completo
En contraste con el medio sumador,
un sumador
completo recibe tres entradas A, B, Cin y calcula dos salidas S y Cout relacionadas como A + B + Cin = S + 3 * Cout.
Suma de tres trits
Si queremos calcular una suma de A + B + Cin, la idea es la misma que antes: utilizamos la preparación de entradas capa por capa. La primera capa recibe A como entrada, la segunda usa B y la última capa de multiplexor simple usa Cin. Aquí hay una forma posible de calcular la salida S:
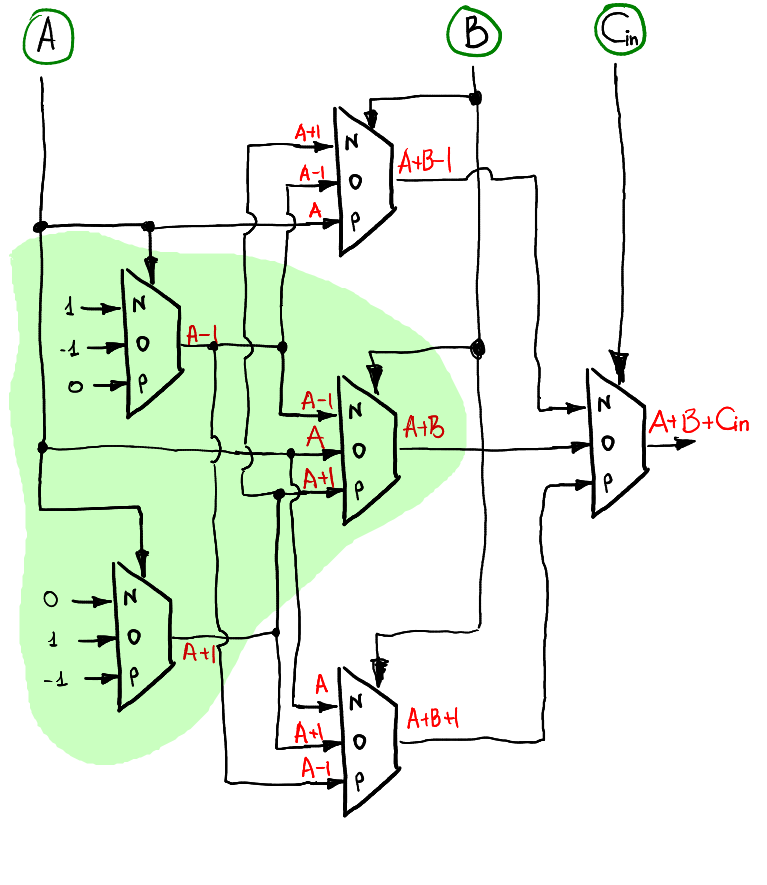
Tenga en cuenta que cuando Cin = 0, se comporta exactamente de la misma manera que el medio sumador, por lo tanto, es natural ver la inclusión (resaltada en verde) de los esquemas del medio sumador en el sumador completo.
Desbordamiento (llevar bandera)
El trit de desbordamiento se puede calcular de la misma manera capa por capa. ¡También incluye el medio sumador!
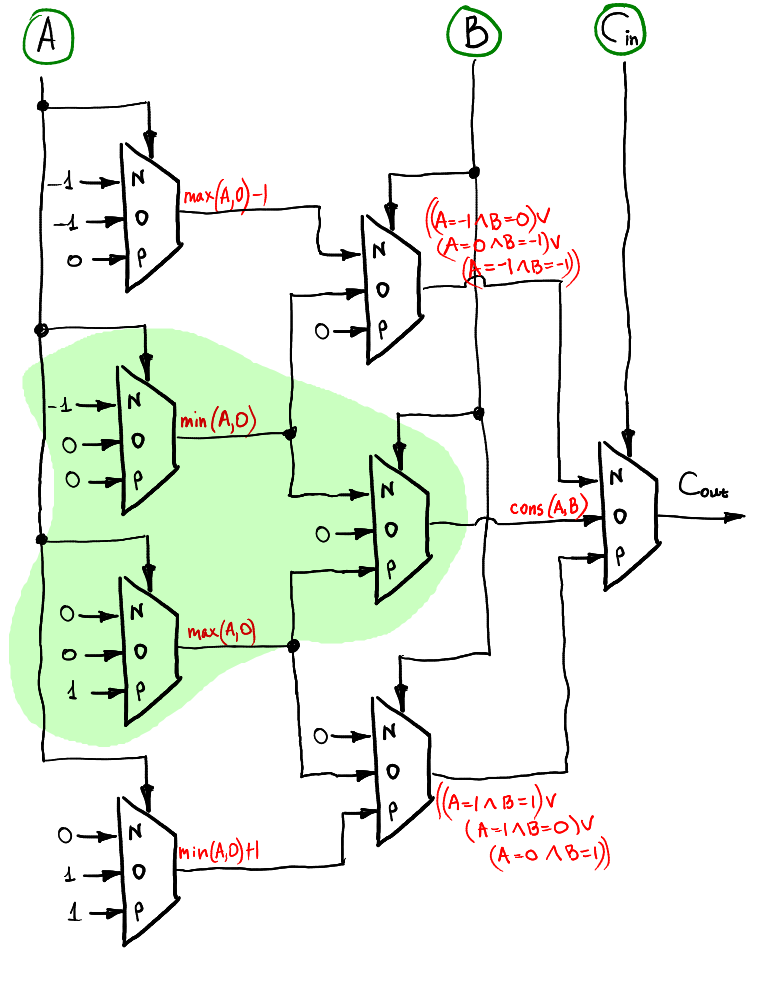
Validación de hardware
Esta vez era demasiado flojo para usar paneles para probar el sumador completo, así que hice este PCB de una capa:

Aquí es después de que el cobre fue grabado:

Las tres tablas siguientes enumeran los 27 estados posibles del sumador completo. Como antes, las fotos están disponibles para cada estado. Tenga en cuenta que la tabla del medio (Cin = 0) es exactamente la misma que para el medio sumador.
La ventaja del sumador completo con respecto al medio sumador es la posibilidad de apilar varios sumadores hasta que obtengamos suficientes trits para representar el número que queremos.
Aquí hay una pila de dos sumadores:

Y aquí cómo resuelve -4 + 2 (el trit menos significativo está a la izquierda):

Por supuesto, no necesitamos un tablero de sumador completo para el trit menos significativo (no tenemos un indicador de acarreo para la entrada del trit menos significativo), sería suficiente un medio sumador.
Conclusión
Este es el final de la introducción a la informática ternaria. ¡Estén atentos para relojes, contadores, memoria y más!