Geekly articles weekly

Computación cuántica en juegos, o volverse loco en serio

Si vives entre locos, debes aprender a estar loco tú mismo

¿Alguna vez has intentado "aprender a estar loco"? Tarea no trivial. Ni siquiera encontrarás una técnica normal, porque todos se vuelven locos a su manera. Mi primer intento: teoría de la conspiración. La teoría no implica práctica, lo que significa que no tienes que trabajar duro. Nuevamente, en cualquier situación, nadie sufrirá.

¿Cómo crear teorías de conspiración?
Crear una teoría de conspiración es relativamente simple. Necesitamos una idea que sea lo suficientemente simple como para ser aceptada por el 90% de la población. Debería ser controvertido para que el 5% de la población pueda explicar al 90% qué idiotas son. Finalmente, necesitamos algunas investigaciones que el 95% de las personas no entienden, pero que el 90% utiliza como argumento "las personas han demostrado ser más inteligentes que nosotros ...".

La computación cuántica es un área excelente para tal estudio. Puede acumular un esquema simple, pero la palabra "cuántico" agregará peso a los resultados.

El objeto de estudio es un juego, porque el objeto se debe a la juventud simple y familiar. ¿Quién participa en la computación cuántica y los juegos? Google

Entonces, teoría herética: después de 5 años, Page y Green decidirán quién será lo principal en Google, y lo harán con la ayuda del juego. Cada uno de ellos tiene un grupo de investigadores. El equipo de AlphaGo con sus redes neuronales de lucha atrajo a sus rivales en Go. Los opositores se vieron obligados a buscar nuevos métodos, y todavía encontraron un instrumento de total superioridad: la computación cuántica.

¿Puedo usar Quantum Computing para juegos? Fácil Demostremos, por ejemplo, que el juego "cazador de zorros" se puede "resolver" en 6 movimientos. En aras de la credibilidad, nos restringimos a 15 qubits (la peculiaridad del editor en línea no emula durante más de quince), por simplicidad, ignoramos las limitaciones de la arquitectura del procesador y la corrección de errores.

Las reglas


Extremadamente simple Hay cinco agujeros dispuestos en una fila (los numeramos como 0-1-2-3-4). En uno de ellos hay un zorro. Todas las noches, el zorro se mueve al siguiente visón hacia la izquierda o hacia la derecha. Cada mañana, el cazador puede marcar un hoyo para elegir. La tarea del cazador es atrapar al zorro. La tarea del zorro es sobrevivir. En teoría, un zorro puede huir de un cazador para siempre. En la práctica, hay una estrategia ganadora: verificar los hoyos 1-2-3-1-2-3. Solo probaré esta estrategia.

Construyendo un esquema


Comencemos con la iniciación de qubits 0-1-2-3-4 (5 agujeros). Aquí puedes editar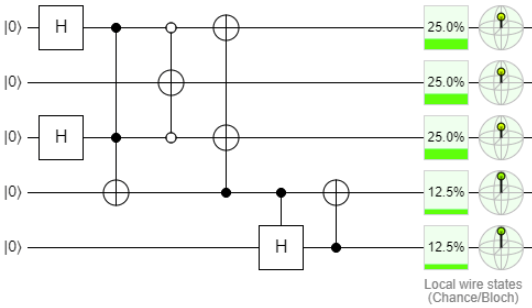


De hecho, después del inicio, tenemos un sistema en el cual, después de la medición, estrictamente un qubit será único. Las probabilidades de "unidad" difieren para cada qubit, pero en nuestro caso esto no es crítico. Debemos dejar espacio para la discusión del esquema (y nuestra teoría al mismo tiempo).

En Q #, obtenemos un código como este:

operation TestStrategy () : (Result) { let res = Zero; using(qubits=Qubit[16]) { // 0..4 - holes // 5 - current movement direction. Zero means "go down", One means "go up" // 6 - Game status. 1 means "fox is free, go further" // 7,8,9,10, 11 - movements history InitFoxHoles(qubits); ResetAll(qubits); // ALWAYS clean after yourself } return Zero; } // Inits fox holes, with almost equal probabilities operation InitFoxHoles(register: Qubit[]) : Unit { body { ResetAll(register); // Step 1 H(register[0]); H(register[2]); // Step 2 (Controlled (X))([register[0],register[2]], register[3]); // Step 3 X(register[0]); X(register[2]); (Controlled (X))([register[0],register[2]], register[3]); X(register[0]); X(register[2]); // Step 4 CNOT(register[3], register[0]); CNOT(register[3], register[2]); // Step 5 (Controlled (H))([register[3]], register[4]); // Step 6 CNOT(register[4], register[3]); } }

TestStrategy probará nuestra estrategia 1-2-3-1-2-3, InitFoxHoles () es responsable solo del inicio de los agujeros de zorro. Verifiquemos la iniciación. Copie TestStrategy, inicie el inicio, mida los primeros 5 qubits y devuelva sus valores.

  operation TestInit(): (Result, Result, Result, Result, Result) { body { mutable res0 = Zero; mutable res1 = Zero; mutable res2 = Zero; mutable res3 = Zero; mutable res4 = Zero; using(qubits=Qubit[16]) { // 0..4 - holes // 5 - current movement direction. Zero means "go down", One means "go up" // 6 - Game status. 1 means "fox is free, go further" // 7,8,9,10, 11 - movements history InitFoxHoles(qubits); set res0 = M(qubits[0]); set res1 = M(qubits[1]); set res2 = M(qubits[2]); set res3 = M(qubits[3]); set res4 = M(qubits[4]); ResetAll(qubits); // ALWAYS clean after yourself } return (res0, res1, res2, res3, res4); } }

Realizaremos la prueba miles de veces (las ejecuciones múltiples son típicas de los algoritmos cuánticos, en algunos lugares incluso necesarios). Código de llamada: debajo del spoiler, resultados: en la pantalla a continuación.

Probar rápidamente el inicio
  static void TestInitiation() { using (var sim = new QuantumSimulator()) { var initedQubitsValues = Enumerable.Range(0, 5) .ToDictionary(qubitIndex => qubitIndex, oneMesaured => 0); for (int i = 0; i < 1000; i++) { (Result, Result, Result, Result, Result) result = TestInit.Run(sim).Result; if (result.Item1 == Result.One) { initedQubitsValues[0]++; } if (result.Item2 == Result.One) { initedQubitsValues[1]++; } if (result.Item3 == Result.One) { initedQubitsValues[2]++; } if (result.Item4 == Result.One) { initedQubitsValues[3]++; } if (result.Item5 == Result.One) { initedQubitsValues[4]++; } } Console.WriteLine($"Qubit-0 initiations: {initedQubitsValues[0]}"); Console.WriteLine($"Qubit-1 initiations: {initedQubitsValues[1]}"); Console.WriteLine($"Qubit-2 initiations: {initedQubitsValues[2]}"); Console.WriteLine($"Qubit-3 initiations: {initedQubitsValues[3]}"); Console.WriteLine($"Qubit-4 initiations: {initedQubitsValues[4]}"); } }




Algo salió mal. Se esperaba una distribución casi uniforme. La razón es simple: en el paso 3, invertí el tercer qubit, en lugar del primero: (Controlado (X)) ([registro [0], registro [2]], registro [3]); No es bueno copiar y pegar.

Arreglamos el código, ejecutamos la prueba:

Iniciación corregida
  // Inits fox holes, with almost equal probabilities operation InitFoxHoles(register: Qubit[]) : Unit { body { ResetAll(register); // Step 1 H(register[0]); H(register[2]); // Step 2 (Controlled (X))([register[0],register[2]], register[3]); // Step 3 X(register[0]); X(register[2]); (Controlled (X))([register[0],register[2]], register[1]); X(register[0]); X(register[2]); // Step 4 CNOT(register[3], register[0]); CNOT(register[3], register[2]); // Step 5 (Controlled (H))([register[3]], register[4]); // Step 6 CNOT(register[4], register[3]); } } }




Ya mejor. El código se puede ver en el nabo, versión Commit 1 .

¿Dónde correr el zorro?


Seleccione el quinto qubit (la numeración comienza desde arriba) bajo la dirección actual del zorro. Estamos de acuerdo en que cero significa un movimiento hacia abajo, una unidad significa un movimiento hacia arriba. Obviamente, si el zorro ya está en el agujero cero, debe moverse hacia abajo. Si el zorro está en el cuarto hoyo, se mueve hacia arriba. En otros casos, el zorro puede moverse hacia arriba y hacia abajo. De acuerdo con estas reglas simples, podemos establecer el "qubit de la dirección actual" a 0, 1, o una superposición de cero y uno. Observamos el código en el repositorio, Commit 2 .


Esquema en el editor.

Código y prueba
 // Select next Fox movement direction, updating qubit 5 // 1 means go up (4 -> 3, 3 -> 2, ... 1 -> 0) // 0 means go down (0 -> 1, 1 -> 2, ... 3 -> 4) operation SetupMovementDirection(qubits: Qubit[]) : Unit { body { // Step 1 CNOT(qubits[4], qubits[5]); // Step 2 (Controlled (H))([qubits[3]], qubits[5]); // Step 3 (Controlled (H))([qubits[2]], qubits[5]); // Step 4 (Controlled (H))([qubits[1]], qubits[5]); } } operation TestMovementDirectionSetup(): (Result, Result, Result, Result, Result, Result) { body { mutable res0 = Zero; mutable res1 = Zero; mutable res2 = Zero; mutable res3 = Zero; mutable res4 = Zero; mutable res5 = Zero; using(qubits=Qubit[16]) { InitFoxHoles(qubits); SetupMovementDirection(qubits); set res0 = M(qubits[0]); set res1 = M(qubits[1]); set res2 = M(qubits[2]); set res3 = M(qubits[3]); set res4 = M(qubits[4]); set res5 = M(qubits[5]); ResetAll(qubits); // ALWAYS clean after yourself } return (res0, res1, res2, res3, res4, res5); } } 


  static void TestMovementDirectionSetup() { using (var sim = new QuantumSimulator()) { List<string> results = new List<string>(); string initedCubit = null; string moveDirection = null; for (int i = 0; i < 1000; i++) { (Result, Result, Result, Result, Result, Result) result = Quantum.FoxHunter.TestMovementDirectionSetup.Run(sim).Result; if (result.Item1 == Result.One) { initedCubit = "0"; } if (result.Item2 == Result.One) { initedCubit = "1"; } if (result.Item3 == Result.One) { initedCubit = "2"; } if (result.Item4 == Result.One) { initedCubit = "3"; } if (result.Item5 == Result.One) { initedCubit = "4"; } if (result.Item6 == Result.One) { moveDirection = "1"; } else { moveDirection = "0"; } results.Add($"{initedCubit}{moveDirection}"); } foreach(var group in results .GroupBy(result => result) .OrderBy(group => group.Key)) { Console.WriteLine($"{group.Key} was measured {group.Count()} times"); } Console.WriteLine($"\r\nTotal measures: {results.Count()}"); } }





Movimiento

Implementado por SWAP controlado. Si el qubit de control es único, cambie hacia abajo. Si el qubit de control es cero, cambiamos.


Esquema en el editor .

Operador Q #
  // Makes a movement based on the 5'th qubit value // 1 means go up (4 -> 3, 3 -> 2, ... 1 -> 0) // 0 means go down (0 -> 1, 1 -> 2, ... 3 -> 4) operation MakeMovement(qubits: Qubit[]) : Unit { body { // Code movement Up // Step 1 mutable qubitsToSwap = [qubits[0], qubits[1]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // Step 2 set qubitsToSwap = [qubits[1], qubits[2]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // Step 3 set qubitsToSwap = [qubits[2], qubits[3]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // Step 4 set qubitsToSwap = [qubits[3], qubits[4]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // COde movement down X(qubits[5]); // Invert direction qubit for the ZeroControlled operations // Step 5 set qubitsToSwap = [qubits[3], qubits[4]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // Step 6 set qubitsToSwap = [qubits[2], qubits[3]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // Step 7 set qubitsToSwap = [qubits[1], qubits[2]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // Step 8 set qubitsToSwap = [qubits[0], qubits[1]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); X(qubits[5]); // Back-invert for the direction qubit } }


Q #: declaración para pruebas
  operation TestFirstMovement(): (Result, Result, Result, Result, Result, Result) { body { mutable res0 = Zero; mutable res1 = Zero; mutable res2 = Zero; mutable res3 = Zero; mutable res4 = Zero; mutable res5 = Zero; using(qubits=Qubit[16]) { InitFoxHoles(qubits); SetupMovementDirection(qubits); MakeMovement(qubits); set res0 = M(qubits[0]); set res1 = M(qubits[1]); set res2 = M(qubits[2]); set res3 = M(qubits[3]); set res4 = M(qubits[4]); set res5 = M(qubits[5]); ResetAll(qubits); // ALWAYS clean after yourself } return (res0, res1, res2, res3, res4, res5); } }


Código C #
  static void TestFirstMove() { using (var sim = new QuantumSimulator()) { List<string> results = new List<string>(); string initedCubit = null; string moveDirection = null; for (int i = 0; i < 1000; i++) { (Result, Result, Result, Result, Result, Result) result = Quantum.FoxHunter.TestFirstMovement.Run(sim).Result; if (result.Item1 == Result.One) { initedCubit = "0"; } if (result.Item2 == Result.One) { initedCubit = "1"; } if (result.Item3 == Result.One) { initedCubit = "2"; } if (result.Item4 == Result.One) { initedCubit = "3"; } if (result.Item5 == Result.One) { initedCubit = "4"; } if (result.Item6 == Result.One) { moveDirection = "1"; } else { moveDirection = "0"; } results.Add($"{initedCubit}{moveDirection}"); } // Holes measurements foreach (var group in results .GroupBy(result => result[0]) .OrderBy(group => group.Key)) { Console.WriteLine($"{group.Key} hole was measured {group.Count()} times"); } // Directions measuremetns foreach (var group in results .GroupBy(result => result[1]) .OrderBy(group => group.Key)) { Console.WriteLine($"{group.Key} direction was measured {group.Count()} times"); } Console.WriteLine($"\r\nTotal measures: {results.Count()}"); } }


El código se puede ver en Commit 3 .

Hacemos 6 movimientos


Finalmente, seleccionamos el sexto qubit para el estado del juego (el zorro es gratis / el zorro no es gratis). La unidad corresponde a un zorro libre. Haremos más movimientos solo con un solo qubit de estado.

Los qubits 7,8,9,10,11 mantendrán un historial de movimientos. Después de cada movimiento, vamos a intercambiar uno de ellos con un qubit de la dirección actual (esto nos permitirá almacenar el historial de movimientos y restablecer el qubit de la dirección actual antes de cada movimiento).

Esquema adjunto .

Operador Q #
  /// Make 6 movements. Every movement is controlled by the 6'th qubit. /// After the every qubit we check if the fox has been captured and invert the 6'th qubit /// Reminder: 6'th qubit equal to One means "Fox is free, go further" operation MakeSixMovements(qubits: Qubit[]) : Unit { body { // Move 1 (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[1], qubits[6]); // Reverse Fox State if it's shot // Move 2 SwapReverseRegister([qubits[5], qubits[7]]); // Move the first move direction to the qubit 7, qubit 5 is Zero again (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[2], qubits[6]); // Move 3 SwapReverseRegister([qubits[5], qubits[8]]); (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[3], qubits[6]); // Move 4 SwapReverseRegister([qubits[5], qubits[9]]); (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[1], qubits[6]); // Move 5 SwapReverseRegister([qubits[5], qubits[10]]); (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[2], qubits[6]); // Move 6 SwapReverseRegister([qubits[5], qubits[11]]); (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[3], qubits[6]); } }


Q #: declaración para pruebas
  operation TestSixMovements(): (Result) { body { mutable res = Zero; using(qubits=Qubit[16]) { ResetAll(qubits); InitFoxHoles(qubits); X(qubits[6]); // At the beginning of the game our fox is alive MakeSixMovements(qubits); set res = M(qubits[6]); ResetAll(qubits); // ALWAYS clean after yourself } return (res); } }


C #: prueba
  static void TestMovements() { using (var sim = new QuantumSimulator()) { int zerosCount = 0; for (int i = 0; i < 1000; i++) { Result result = Quantum.FoxHunter.TestSixMovements.Run(sim).Result; if(result == Result.Zero) { zerosCount++; } } Console.WriteLine($"\r\nTotal zeroes: {zerosCount}"); } }


Buscamos Commit 4 .

Toques finales


Tenemos un error en el circuito. Como probamos la estrategia 1-2-3-1-2-3, revisamos cada hoyo dos veces. En consecuencia, habiendo atrapado al zorro en el primer movimiento, pasaremos por el qubit de estado dos veces (en el primer movimiento y el cuarto).

Para evitar esta situación, usamos 12 qubits para arreglar el estado después de los movimientos 4-5-6. Además, agregamos la definición de victoria: si al menos uno de los qubits de estado se convierte en cero, ganamos.

El esquema final .

Q #: arregla el operador de 6 movimientos
  operation MakeSixMovements(qubits: Qubit[]) : Unit { body { // Move 1 (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[1], qubits[6]); // Reverse Fox State if it's shot // Move 2 SwapReverseRegister([qubits[5], qubits[7]]); // Move the first move direction to the qubit 7, qubit 5 is Zero again (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[2], qubits[6]); // Move 3 SwapReverseRegister([qubits[5], qubits[8]]); (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[3], qubits[6]); // Move 4 SwapReverseRegister([qubits[5], qubits[9]]); (Controlled(SetupMovementDirection))([qubits[6], qubits[12]],(qubits)); (Controlled(MakeMovement))([qubits[6], qubits[12]],(qubits)); CNOT(qubits[1], qubits[12]); // Move 5 SwapReverseRegister([qubits[5], qubits[10]]); (Controlled(SetupMovementDirection))([qubits[6], qubits[12]],(qubits)); (Controlled(MakeMovement))([qubits[6], qubits[12]],(qubits)); CNOT(qubits[2], qubits[12]); // Move 6 SwapReverseRegister([qubits[5], qubits[11]]); (Controlled(SetupMovementDirection))([qubits[6], qubits[12]],(qubits)); (Controlled(MakeMovement))([qubits[6], qubits[12]],(qubits)); CNOT(qubits[3], qubits[12]); } }


P #: arregle la estrategia de prueba del operador 1-2-3-1-2-3
  operation TestStrategy () : (Result) { // 0..4 - holes // 5 - current movement direction. Zero means "go down", One means "go up" // 6 - Game status. 1 means "fox is free, go further" // 7,8,9,10, 11 - movements history // 12 - another qubit of the fox live. 1 means "fox is still free, go further" // 13 Result qubit. If it's zero, the fox is alive body { mutable res = Zero; using(qubits=Qubit[14]) { ResetAll(qubits); // Init fox positions and the fox' live InitFoxHoles(qubits); X(qubits[6]); // At the beginning of the game our fox is alive X(qubits[12]); // The second qubit of the fox live. If it's one - the fox is alive. // Make moves MakeSixMovements(qubits); // Measure results. If the 13'th qubit is zero the fox is alive X(qubits[6]); X(qubits[12]); CNOT(qubits[6], qubits[13]); CNOT(qubits[12], qubits[13]); CCNOT(qubits[6], qubits[12], qubits[13]); set res = M(qubits[13]); ResetAll(qubits); // ALWAYS clean after yourself } return (res); } }


C #: ejecutar la verificación final
  static void RunFoxHunt() { Stopwatch sw = new Stopwatch(); sw.Start(); using (var sim = new QuantumSimulator()) { var foxSurvives = 0; var hunterWins = 0; for (int i = 0; i < 1000; i++) { var result = (Result)(TestStrategy.Run(sim).Result); if (result == Result.Zero) { foxSurvives++; } else { hunterWins++; } } Console.WriteLine($"Fox survives: \t{foxSurvives}"); Console.WriteLine($"Hunter wins: \t{hunterWins}"); } sw.Stop(); Console.WriteLine($"Experiment finished. " + $"Time spent: {sw.ElapsedMilliseconds / 1000} seconds"); }



Comprometerse 5 .

Lo que sigue de esto


En principio, el esquema se puede optimizar tanto en el número de qubits como en el número de operaciones. La optimización trivial para la cantidad de qubits es deshacerse de qubit-13, devolviendo solo 6 y 12. Optimización para operaciones: para realizar el primer disparo inmediatamente después del inicio. Sin embargo, dejemos este trabajo a los ingenieros de Google.

Como puede ver, cualquiera que esté familiarizado superficialmente con la computación cuántica puede jugar con seguridad al "cazador de zorros". Si tuviéramos un poco más de qubits, podríamos encontrar la solución óptima y no verificar la existente. Es completamente posible que el tic-tac-toe (y su versión cuántica), las damas, el ajedrez, Go caigan a continuación.

Al mismo tiempo, el tema de la "solvencia" de juegos como DotA, Starcraft y Doom permanece abierto. La computación cuántica se caracteriza por almacenar todo el historial de clics. Tomamos APM (acciones por minuto) de 500, multiplicamos por la cantidad de jugadores, multiplicamos por la cantidad de minutos, agregamos la aleatoriedad del juego en sí; la cantidad de qubits necesarios para almacenar toda la información crece demasiado rápido.

Por lo tanto, elegir un juego en una pequeña competencia entre Brin y Page puede jugar un papel decisivo. Sin embargo, la generación de un juego "igualmente difícil" para computadoras clásicas y cuánticas merece su propia teoría.

Source: https://habr.com/ru/post/437352/

More articles:


All Articles