Que debemos construir un camino. Parte 1

El itinerario diario de la mayoría de nosotros se limita a viajar desde casa al trabajo y viceversa. Y el obstáculo más difícil que puede ralentizar nuestro movimiento son los atascos. Pero en nuestro país hay una gran cantidad de lugares donde solo puedes subirte a vehículos especiales.

Tal transporte es bueno si no necesita transportar grandes volúmenes de carga o viajar a áreas inaccesibles de manera regular. Entonces ya deberíamos pensar en la construcción de infraestructura, cuyo movimiento es posible en el transporte civil habitual.

Y es bueno si toda la complejidad del diseño de una ruta futura radica en encontrar una regla y un lápiz para dibujar una línea recta en el mapa que conecte un par de objetos. Pero, por desgracia, nuestra realidad es muy diferente a esto. ¿Qué pasa si el terreno que vuela sobre él se parece a un buen pedazo de queso suizo?

Durante más de un año, hemos estado trabajando con colegas del laboratorio de investigación de Diseño Digital para crear una herramienta que pueda construir varias redes de comunicación en modo automático. Para más detalles, bienvenido a cat.

Como empezó todo

Por lo general, los viajes a lugares tan remotos se deben a ciertos beneficios financieros. Y aunque a menudo se sabe de antemano que el desarrollo de estas áreas traerá buenas ganancias, ¿por qué no ahorrar dinero en cosas que se pueden hacer sin dificultades especiales? ¿Qué sucede si una ruta diseñada de manera más competente nos permite no construir varios kilómetros adicionales de la carretera?

Pero solo la disponibilidad de carreteras para recibir ganancias significativas es claramente insuficiente. Y básicamente solo es traído por depósitos minerales. Por lo tanto, además de las carreteras, es necesario diseñar una red de varias tuberías, una red de tuberías de agua, una red de líneas eléctricas con subestaciones eléctricas colocadas correctamente. Toda esta infraestructura puede designarse como objetos lineales.

Y cuando un ingeniero se enfrenta a la tarea de diseñar una red de comunicaciones en el terreno con condiciones complejas de ingeniería y geológicas, una tarea analítica increíblemente compleja recae sobre él.

¿Cómo no entrar en la zona de inundación del río? ¿Cómo minimizar el camino en los suelos de permafrost? ¿Cómo ahorrar en la cantidad de colchón de arena al tender una carretera a través de un pantano? ¿Dónde conseguir arena para esta almohada?

Esta es solo una pequeña fracción de las preguntas que se hace un ingeniero durante el trabajo y, sin embargo, aún debe tener en cuenta varios GOST y SNiP. Y bueno, si quieres conectar solo dos objetos, y si hay un par de docenas de objetos?

Por lo tanto, la industria del diseño necesita urgentemente una herramienta que pueda calcular tanto el costo de los objetos lineales diseñados por un ingeniero como la capacidad de construirlos en modo automático.

Datos

Lo primero que tuvimos que enfrentar cuando comenzamos la tarea fue la búsqueda de datos. ¿Qué datos se requieren? ¿Dónde conseguirlos? Y si la segunda pregunta puede resolverse con la ayuda del usuario, para comprender la primera pregunta necesitamos análisis serios.

Y los datos para el cálculo correcto requieren realmente mucho, comenzando por la marca más banal del área en la que se marcan los lagos y ríos, varios pantanos, así como áreas kársticas, en las que se recomienda no construir debido a la amenaza de colapso. Por lo tanto, además de las áreas que se pueden ver desde el satélite, aquí también se requieren datos de estudios geológicos del área.

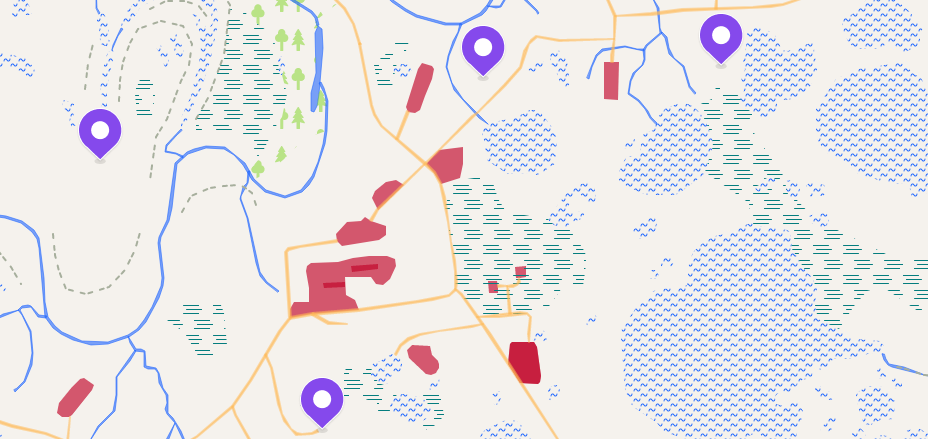
Pero no todos los datos están limitados a objetos naturales en nuestro país. También hay un montón de cosas que fueron creadas por el hombre. Por ejemplo, en el caso de la construcción de carreteras, podemos usar las carreteras que se construyeron anteriormente. Pero en la construcción de tuberías, el uso de la infraestructura existente está lejos de ser siempre posible. Dado que la conexión de una nueva tubería a una red existente puede no pasar el cálculo hidráulico.

Además de la reutilización de lo que fue creado previamente por el hombre, también se deben tener en cuenta varias restricciones en la construcción cerca de cualquier objeto. Por ejemplo, para la construcción de líneas eléctricas, debe tener en cuenta las muescas de los lugares de habitación humana dependiendo del voltaje en la línea eléctrica misma.

Pero no es del todo correcto considerar el cálculo del problema solo en un avión, ya que además del terreno plano, hay áreas con una gran diferencia de elevación, en las que tampoco se puede llevar a cabo la construcción.

Obtener datos sobre el terreno es un proceso mucho más simple que los datos sobre el marcado de áreas y la infraestructura existente. Para simplificar el desarrollo, utilizamos datos de elevación SRTM (Shuttle Radar Topography Mission) abiertos que cualquiera puede obtener.

Entonces, tenemos los datos, sabemos dónde podemos construir, dónde no podemos construir, hay costos de construcción para diferentes áreas del terreno. Tenemos una región, tiene un conjunto de objetos que queremos conectar a una sola red de comunicación. En términos matemáticos, esto parecerá una búsqueda de una solución al problema de Steiner.

Un poco de matemática

Se sabe que cada fórmula reduce a la mitad el número de lectores, por lo que redujimos drásticamente esta sección ...

Para optimizar la ruta de la instalación lineal diseñada, es necesario poder calcular su costo de construcción. Cada objeto lineal se puede representar como una polilínea $$$L = \ {A_i, B_i \} _ {i = 0} ^ n$ que consiste en segmentos $$$AB_ {i}$ .
El costo de construcción de cada sección recta se puede representar como un valor de función $$$C_ {AB_ {i}}$ , donde cada segmento se especifica paramétricamente:

$$$$ display $$ {\ displaystyle AB_i \ colon \ left \ {{\ begin {alineado} & s = s \ left (t \ right) - \ mbox {curva parametrizada}, \\ & h = h \ left (s (t ) \ right) - \ mbox {función de altura de elevación}, \\ & c = c \ left (s (t) \ right) - \ mbox {función del costo unitario de construcción en un punto}, \\ \ end {alineado}} \ right .} $$ display $$

donde $$$t \ in \ left [0, 1 \ right]$ - parametrización del segmento.

$$$C_ {AB_i} = \ int \ limits_ {AB_i} c \ left (s (t) \ right) \ sqrt {\ left [g_ {xy} (s (t)) + \ frac {\ partial h} {\ parcial s_x} \ cdot \ frac {\ partial h} {\ partial s_y} \ right] \ dot {s} _ {x} \ dot {s} _ {y}} dt$ donde $$$g$ - el tensor métrico de la superficie de la Tierra sin tener en cuenta el relieve, es decir, en palabras simples, la función de medir la distancia en la superficie de la Tierra.

Debido al hecho de que nuestro planeta tiene la forma de un geoide, es necesario usar fórmulas especiales para medir distancias. Para esto usamos la fórmula de Haversinus. En él, la forma del planeta parece una esfera, pero esto es suficiente para nuestros propósitos, ya que el error de medición es de aproximadamente 0.3% , y la velocidad de cálculo de distancias por este método sigue siendo alta.

Enfoques para encontrar la mejor manera

Pero antes de pasar a unirte a un grupo de objetos, debes aprender a encontrar el camino óptimo entre los dos. Dos formas de hacer esto vienen a la mente de inmediato:

1. construya un gráfico y luego aplique los métodos de búsqueda de ruta más cortos;
2. use una solución basada en métodos de optimización.

Al implementar el primer método, tenemos un problema asociado con el método de construir un gráfico para obtener la mayor precisión posible de la solución. Es necesario encontrar un equilibrio entre la cantidad de vértices y aristas en el gráfico, la calidad de la solución y el tiempo necesario para calcularla.

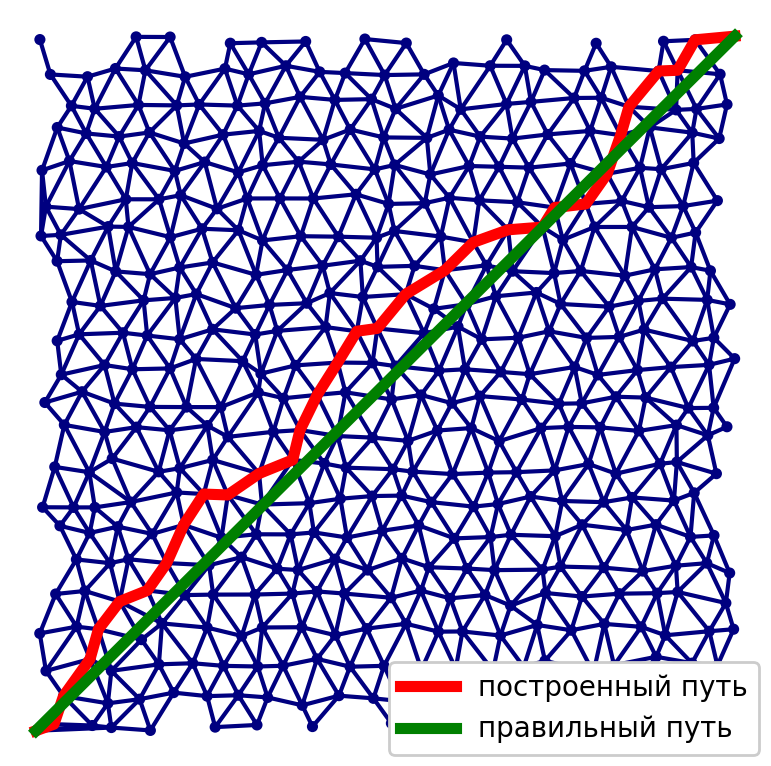
En el segundo caso, el principal problema son los mínimos locales. Es fácil elegir un caso en el que la solución no converja o esté lejos de ser óptima. Dado que la solución obtenida por este método depende increíblemente de la aproximación inicial. Si tenemos una buena aproximación inicial, el resultado será de alta calidad.

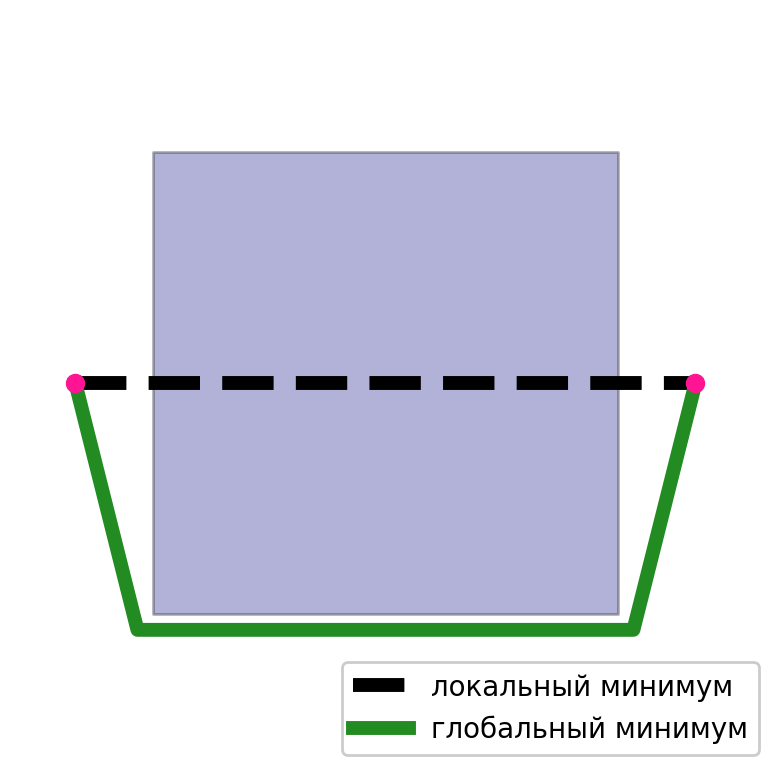
Entonces, tenemos dos enfoques para resolver este problema. El primero tiene una calidad bastante baja, pero no hay problema de mínimos locales. El segundo tiene un problema de mínimos locales, pero una solución de alta calidad. Y si combina correctamente estos dos enfoques, las deficiencias de cada uno desaparecerán. Tomamos la solución obtenida en el gráfico como una aproximación inicial y luego le aplicamos métodos de optimización.

En esta parte del artículo, consideraremos exactamente la solución propuesta para este problema en el gráfico.

Selección de herramienta

Se ha delineado un plan de acción, solo queda "codificarlo". Como en la etapa inicial de redacción de la solicitud teníamos poco conocimiento sobre el área temática, necesitábamos un lenguaje flexible para que, en caso de algunos errores de cálculo arquitectónicos, reescribiéramos el código completo para un par de latas de cerveza de la tarde. Opcionalmente, también quería bibliotecas para todas las ocasiones, a fin de no recurrir a la invención de las bicicletas. Por lo tanto, Python fue elegido como el lenguaje de programación principal.

En la aplicación, utilizamos una impresionante pila tecnológica, que no se limita a lo siguiente:

• bien proporcionado para trabajar con datos geométricos como polígonos y polilíneas;
• geopandas para trabajo conveniente con bien proporcionado ;
• scipy para almacenar el gráfico calculado y encontrar el camino más corto en él, así como encontrar los árboles de expansión mínima;
• PyTorch para trabajar con la función de costo;
• Almohada para trabajar con imágenes.

Implementación

El módulo se puede dividir en varias etapas:

• generación de función de costo;
• generación de cuadrícula computacional;
• construir un gráfico basado en una cuadrícula;
• ponderación de grafos;
• cálculo de los caminos más cortos en un gráfico.

Dado que los bordes del gráfico son segmentos, podemos ponderar estos bordes calculando el valor de una determinada integral, que se presenta arriba. Pero hay muchos bordes en el gráfico y, en consecuencia, los valores de los costos y las alturas deberán obtenerse para una gran cantidad de puntos, lo que puede llevar mucho tiempo.

Inicialmente, la idea era encontrar el costo unitario de construcción determinando si un punto pertenece a un polígono. Pero esta idea se observó debido a la alta complejidad algorítmica de este enfoque, ya que puede haber muchos polígonos, y cada uno de ellos tiene una gran cantidad de vértices.

Por lo tanto, para resolver este problema, podemos representar todos los polígonos que tenemos en forma de imagen, que en forma matemática es una matriz. Por lo tanto, podemos obtener el costo unitario de construcción en un punto más allá de O (1) y, por lo tanto, podemos obtener el costo de construir una costilla en particular con alta precisión.

Ahora estamos listos para construir un gráfico, pero no hay una forma única y correcta de construirlo para obtener soluciones de alta precisión. Para construir un gráfico, es necesario generar una cuadrícula computacional, es decir, un conjunto de puntos en la región en consideración, conectados en el orden correspondiente por segmentos que forman las caras de las celdas. Las cuadrículas se pueden dividir en dos tipos: uniformes y desiguales.

El modelo de cuadrícula uniforme describe las coordenadas de puntos individuales, de modo que la distancia entre los nodos de la cuadrícula es la misma. Una cuadrícula desigual aparece como un conjunto aleatorio de puntos individuales.

El uso de una cuadrícula uniforme no siempre dará un resultado de alta calidad para encontrar el camino más corto, por lo tanto, es necesario probar este enfoque en una cuadrícula desigual. La más versátil es la malla triangular.

La cuadrícula se generó introduciendo ruido con cierto coeficiente en una cuadrícula rectangular uniforme y luego aplicando puntos de triangulación de Delaunay para este conjunto de puntos.

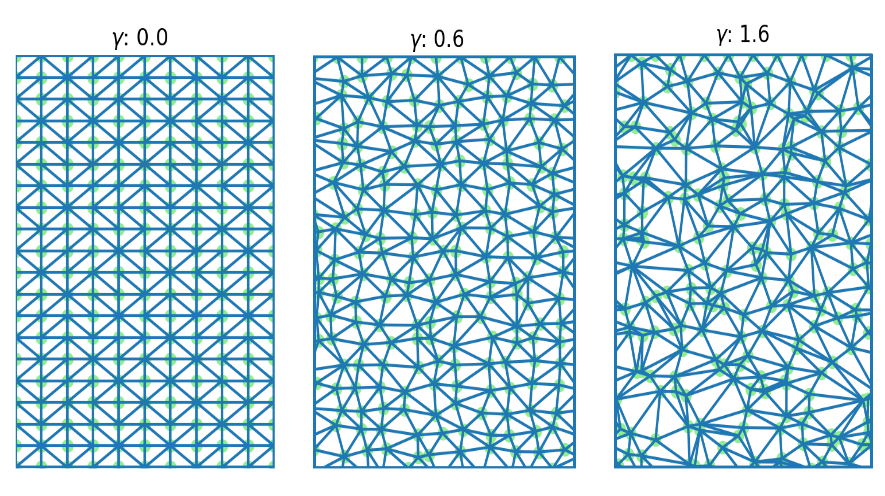
La eficacia de las cuadrículas construidas se probó en varios mapas modelo del área, que tuvieron en cuenta los diferentes costos de las regiones y el alivio, y luego se realizó una comparación con la solución obtenida analíticamente. Al buscar la longitud del borde del gráfico y el coeficiente de introducción de ruido en la cuadrícula uniforme, se encontraron parámetros óptimos para construir la ruta óptima entre dos puntos.

Problemas mayores

Al principio todo salió bien, el algoritmo calculó las redes óptimas, pero una vez que hubo un problema con la calidad de la ruta construida. El caso era bastante simple: había que conectar dos objetos en un mapa bastante largo. El algoritmo no quería construir una ruta que obviamente fuera correcta.

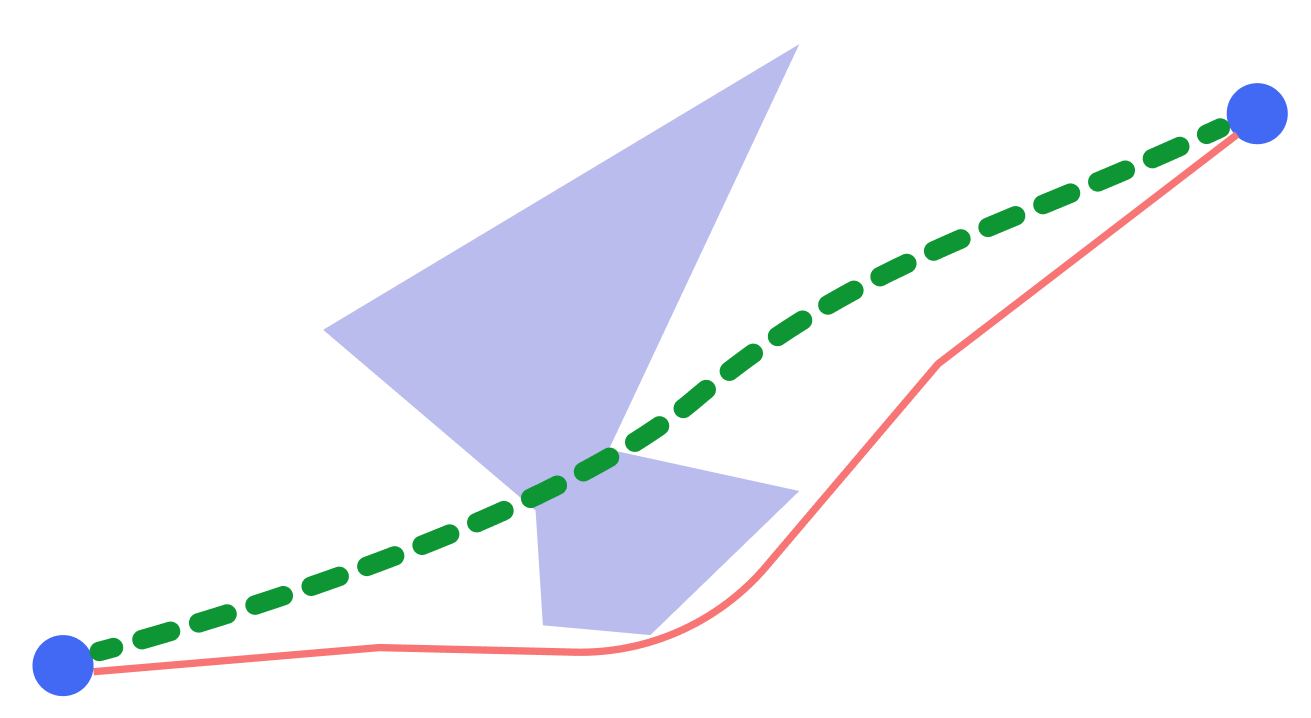
El problema, como siempre, fue con la cuadrícula computacional. Continuamos nuestros experimentos con la apariencia de las cuadrículas y llegamos a la conclusión de que conectar los vértices a un gráfico, donde cada vértice está conectado a los n vecinos más cercanos, es la solución a nuestros problemas.

Redes

Después de que aprendimos cómo encontrar caminos óptimos entre dos puntos, el siguiente paso fue resolver el problema de construir una red óptima de objetos lineales. Los algoritmos encontrados en la literatura para construir árboles de Steiner en gráficos están orientados a problemas más generales y, por lo tanto, serán ineficaces en nuestro caso. Nuestro gráfico es muy escaso, con un pequeño número de vértices terminales, en relación con el número total de vértices en el gráfico, y nuestra tarea también se aplica. Por lo tanto, por varias otras razones, se decidió desarrollar nuestro propio algoritmo que utiliza una cierta heurística para construir de manera efectiva una red óptima.

La descripción del algoritmo para construir la red óptima en el gráfico para nuestro caso es un tema para una publicación separada, no lo consideraremos aquí. Dado que al calcular una tarea real, es necesario tener en cuenta muchas condiciones adicionales de la industria de la construcción que son relevantes para el usuario final, que imponen ciertas restricciones en el algoritmo utilizado.

Caso real

Entonces, ahora pasamos a los resultados del algoritmo. Nuestra tarea es conectar un conjunto dado de objetos con una red de comunicación. La comparación de los resultados del algoritmo ocurrió con una red de carreteras previamente construida. La longitud total de la red existente es 153.5 km versus 122.6 km para la calculada. Esto proporciona una reducción de aproximadamente un 25% en la longitud de la red de carreteras, lo que finalmente ahorrará entre un 5 y un 15% en los costos de construcción de capital.

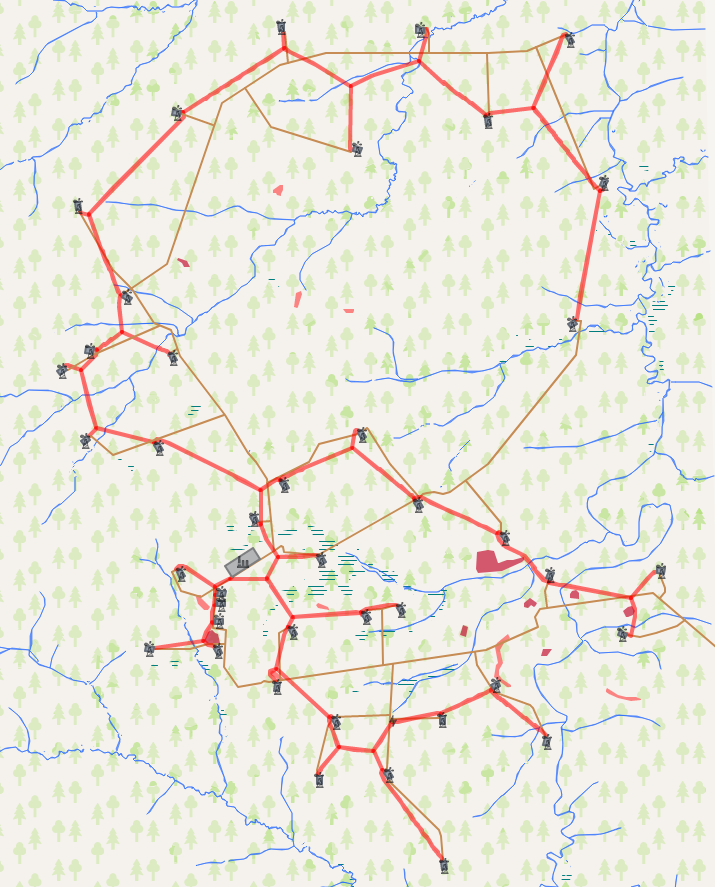
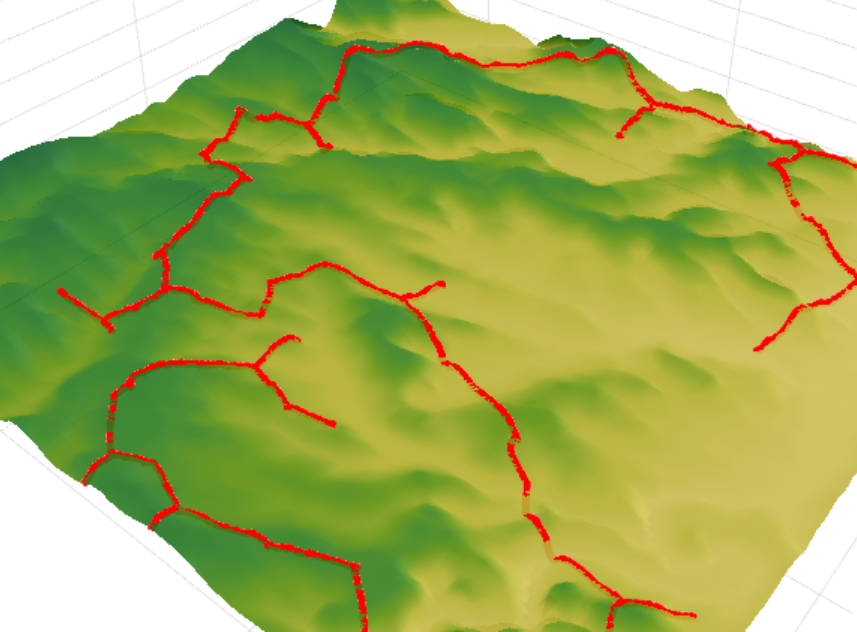
Puede ver más de cerca los resultados de cálculo aquí .

Una descripción de los métodos de optimización utilizados estará en la siguiente parte del artículo.