Muchos desarrolladores creen que el diseño automático es un freno y un problema, y es extremadamente difícil depurarlo. Y es bueno si esta conclusión se hace sobre la base de mi propia experiencia, y a veces es solo "escuché, ni siquiera intentaré hacerme amigo de él".
Pero quizás la razón no está afuera, sino adentro. Por ejemplo, las aves más peligrosas del mundo del casuario no atacarán a las personas sin ningún motivo, solo por defensa propia. Por lo tanto, intente asumir por un segundo que esto no es malo en el diseño automático, y que no lo entiende lo suficiente y no sabe cómo cocinar. Esto es lo que hizo Anton Sergeyev y profundizó en la teoría para comprender todo exactamente. Se nos ofrece un resumen sobre los fundamentos matemáticos del diseño automático.
Auto Layout es un
sistema de diseño . Antes de profundizar en ello, hablemos de la composición tipográfica moderna en general. Luego, tratemos con
el diseño automático : descubriremos
qué tarea resuelve y cómo lo hace. Consideremos las
características en la implementación del diseño automático en iOS e intentemos desarrollar
consejos prácticos que puedan ayudarlo a trabajar con él.
Esta historia estará muy cerca de un artículo matemático, por lo que primero estamos de acuerdo en la notación para hablar el mismo idioma.
Sobre el orador: Anton Sergeev (
antonsergeev88 ) trabaja en el equipo Yandex.Mart, se ocupa del cliente móvil para Maps en iOS. Antes del desarrollo móvil, se ocupó de los sistemas de control de plantas de energía, donde el costo de los errores en el código es demasiado alto para ser tolerado.
Designaciones
Los sistemas de ecuaciones lineales nos son familiares desde la escuela: están indicados por un paréntesis y su solución ya no existe. Además, los sistemas de ecuaciones lineales tienen entidades que operan con diseño automático: restricciones. Están indicados por una línea recta.
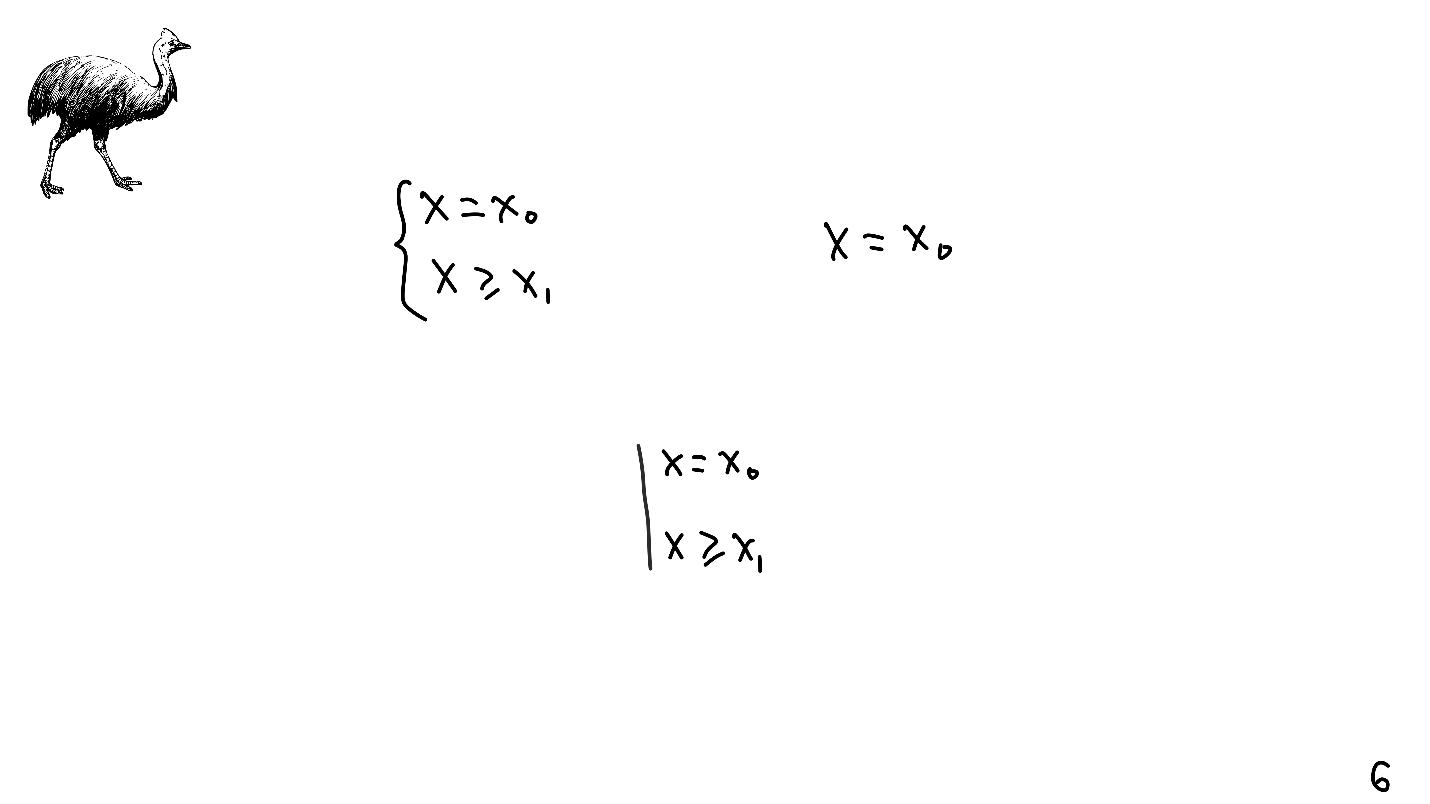
El pájaro extraño y, como ya sabemos, peligroso, no se pinta accidentalmente en la esquina superior del tobogán. En honor al casuario (lat. Cassowary), que, por supuesto, vive en Australia, se nombra un algoritmo en todos nuestros iPhones.
El diseño automático tiene sus propias limitaciones, las designaremos con colores en orden de prioridad: rojo: obligatorio; amarillo - alto; azul - bajo.
Diseño
Cuando estaba preparando la presentación, coloqué varios elementos en la pantalla, por ejemplo, un casuario. Para hacer esto, determiné que el casuario es una imagen rectangular. Debe organizarlo en una hoja que tenga ejes y su propio sistema de coordenadas, y para esto determiné las coordenadas de la esquina superior izquierda, el ancho y la altura.
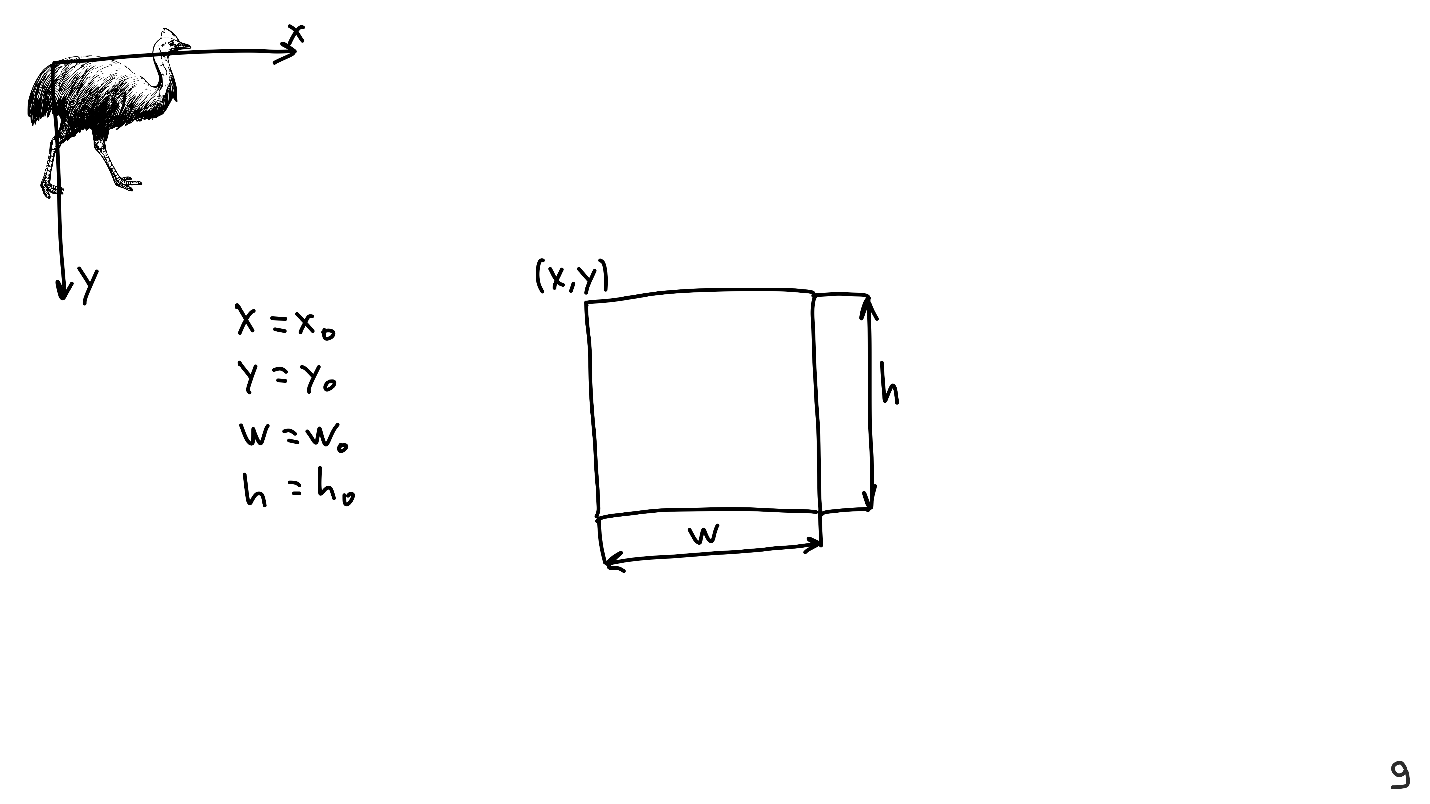
Conocer estos cuatro valores es suficiente para representar cualquier Vista.
Algoritmo No. 1
Al colocar el casuario en la hoja, describimos discretamente el primer algoritmo de diseño:
- determinar las coordenadas y tamaños;
- aplicarlos a UIView.
El algoritmo funciona, pero es bastante difícil de usar, por lo que lo simplificaremos aún más.
Supongamos que a continuación hay una solución para algún sistema de ecuaciones lineales.
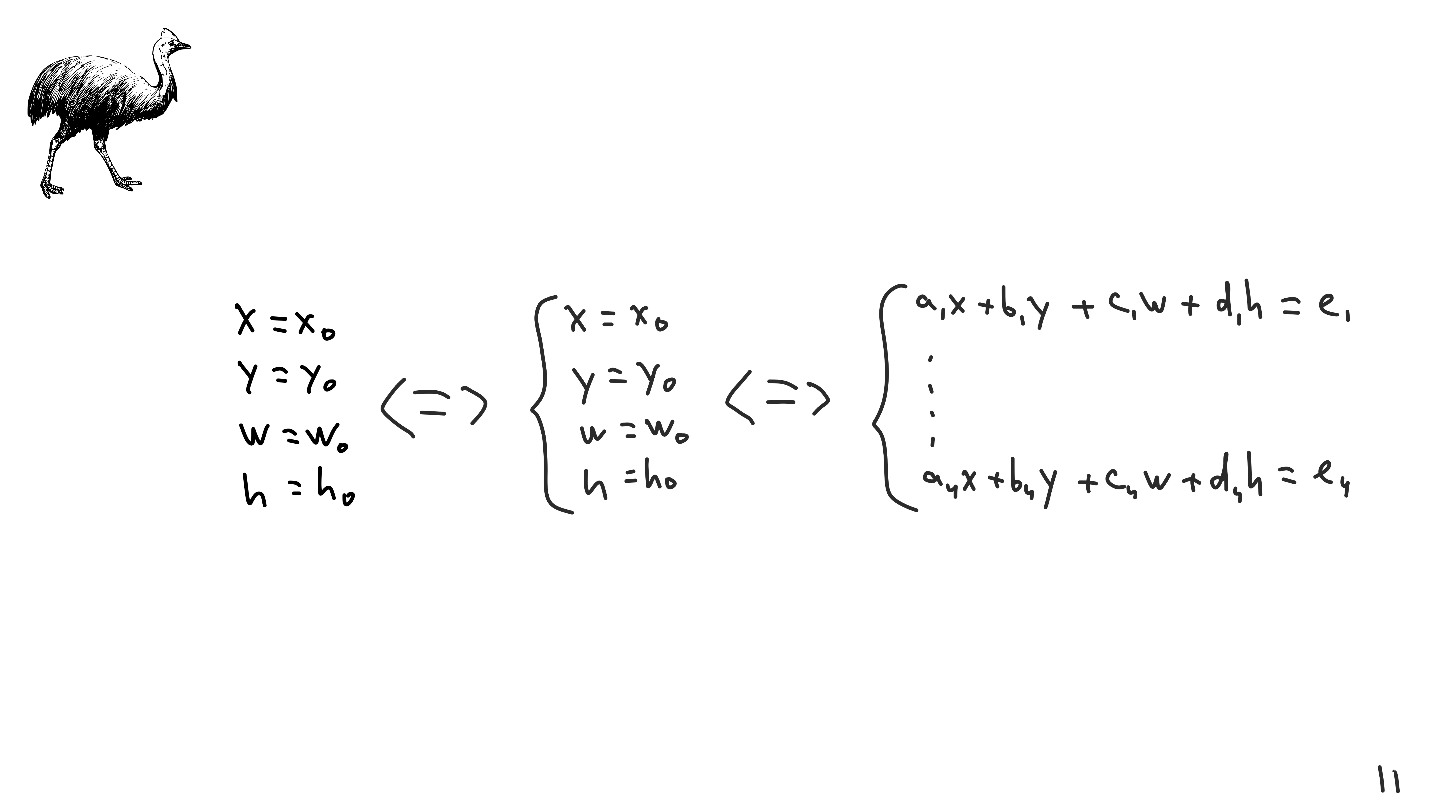
El sistema de ecuaciones lineales es especial porque muchas operaciones se definen sobre él: doblar líneas, multiplicarlas por constantes, etc. Estas operaciones se llaman transformaciones lineales y, con su ayuda, el sistema se reduce a una forma arbitraria.
La belleza de las transformaciones lineales es que son reversibles. Esto nos lleva a una idea interesante y bastante sutil con la que comienza todo el diseño moderno.
Que haya una Vista: un rectángulo con sus coordenadas y tamaño. Queremos organizarlo para que el centro coincida con el punto dado. Modelamos el centro usando transformaciones lineales: la
coordenada de la esquina superior izquierda + la mitad del ancho .
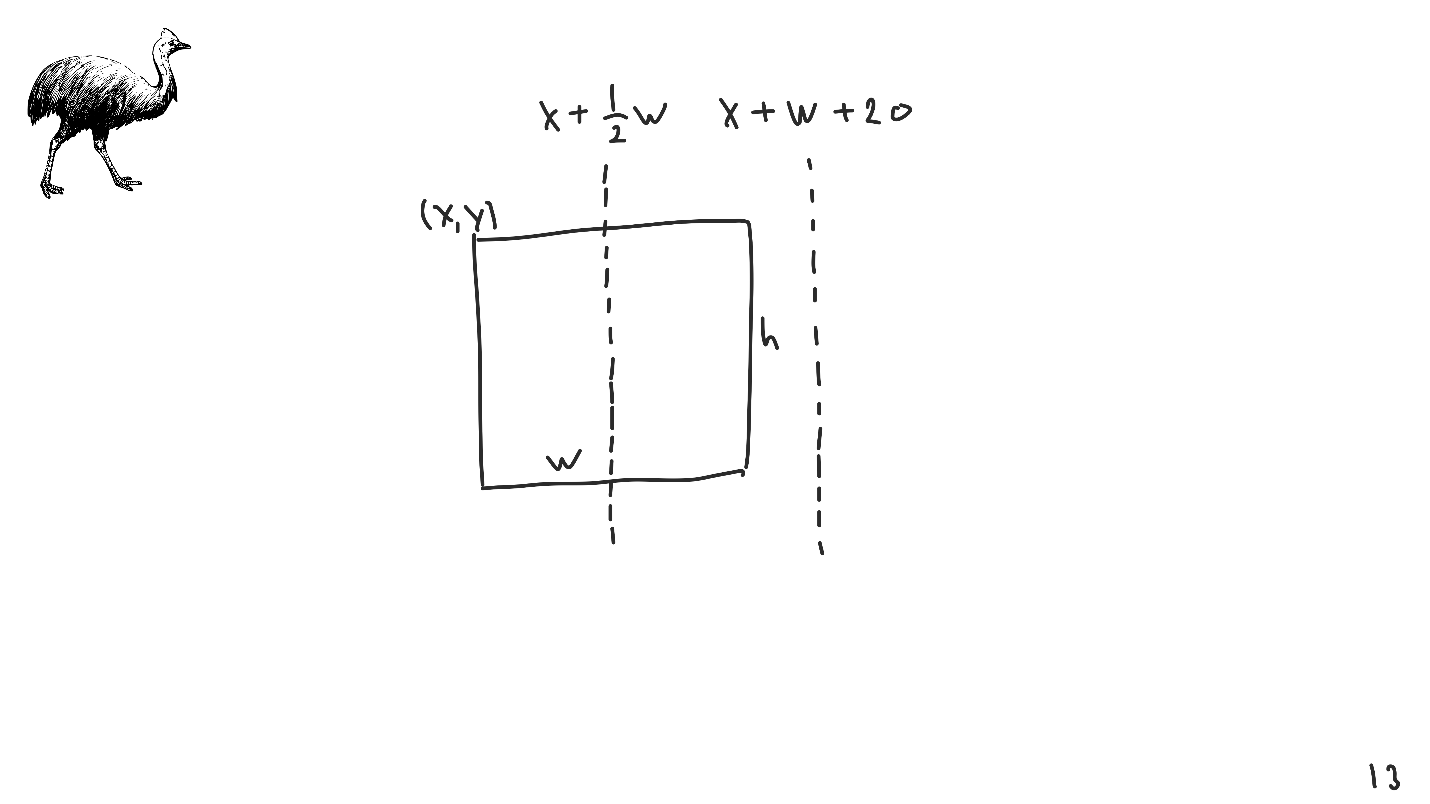
Modelamos el centro por transformación lineal, no fue así: solo existían las coordenadas del punto superior izquierdo, ancho y alto.
Del mismo modo, puede simular cualquier otra sangría, por ejemplo, 20 puntos desde la esquina derecha.
Es la idea de las transformaciones lineales lo que nos permite crear varios sistemas de composición tipográfica.
Considere un ejemplo elemental. Escribimos un sistema con el que establecemos las coordenadas del lado medio y derecho, el ancho y la relación entre ancho y alto. Resolvemos el sistema y obtenemos la respuesta.
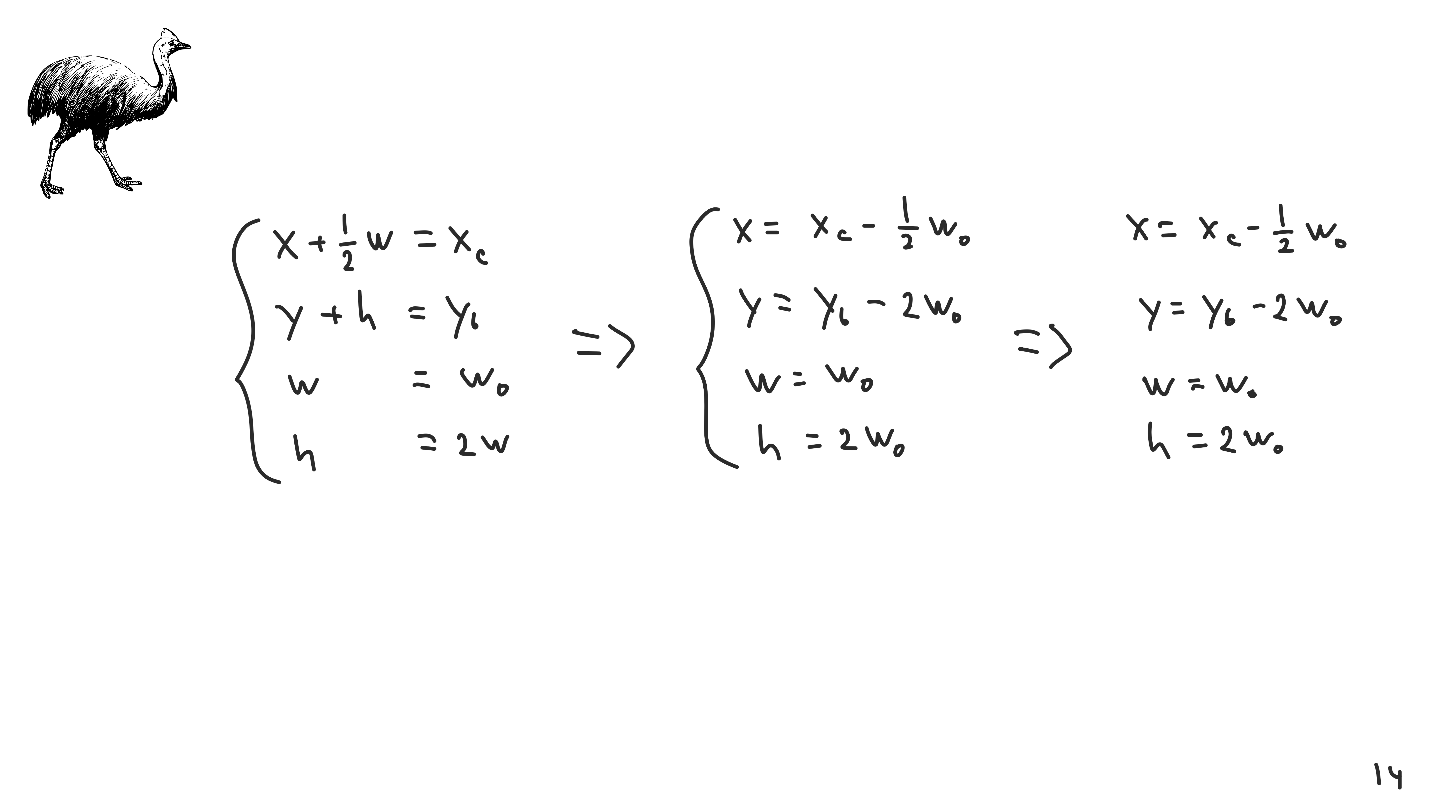
Entonces llegamos al segundo algoritmo.
Algoritmo No. 2
La segunda iteración del algoritmo consta de los siguientes elementos:
- conforman un sistema de ecuaciones lineales;
- nosotros lo resolvemos;
- aplicar la solución a UIView.
Imagine que estuviéramos en el siglo XX, en un momento en que los equipos informáticos recién estaban en pañales, y fuimos los primeros en crear nuestro propio sistema de diseño. Inventado, empaquetado, entregado al usuario, y él comienza a usarlo: completa los parámetros iniciales y lo transfiere a nuestro sistema.
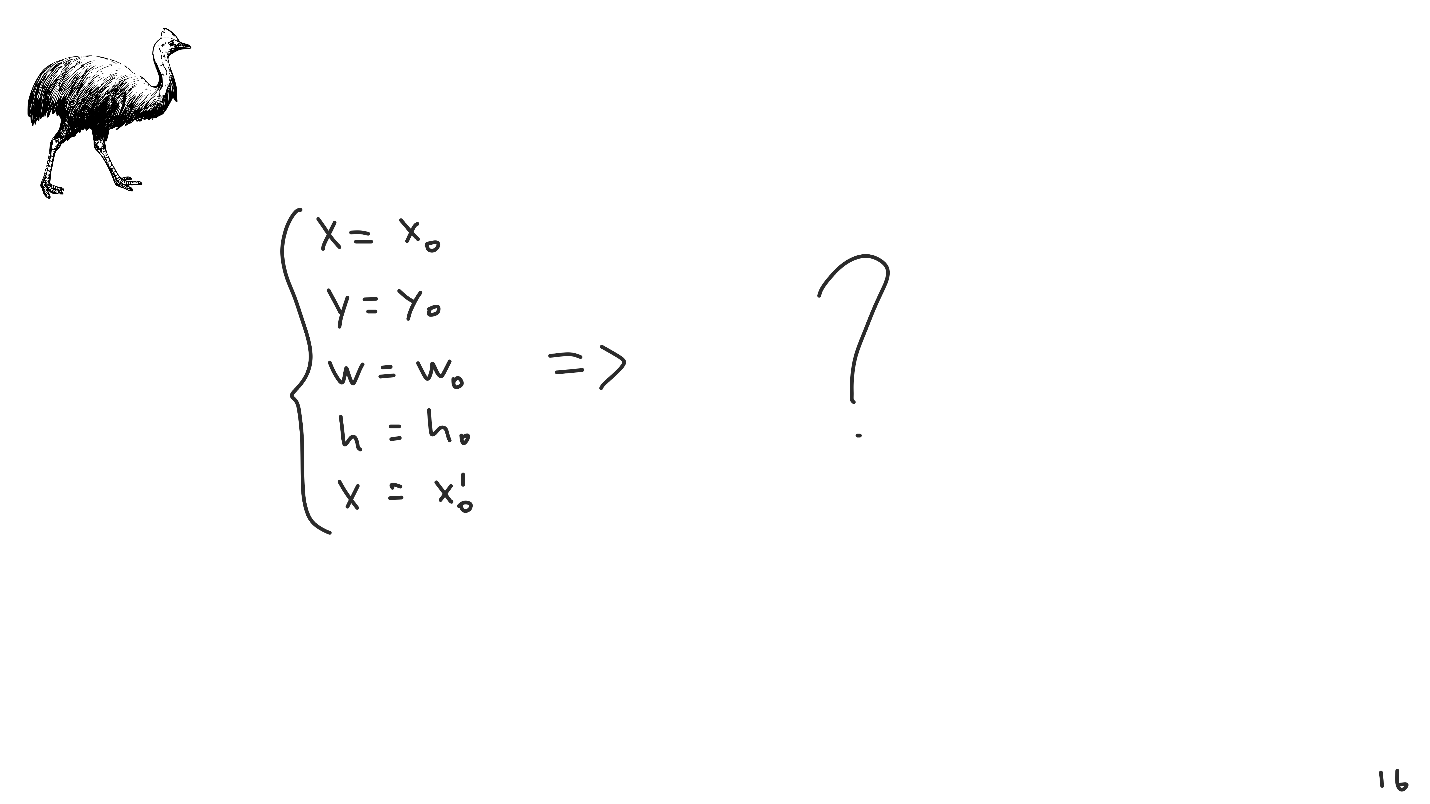
Hay un problema: este sistema no tiene una solución única. El problema no es excepcional, absolutamente todos los sistemas de diseño se topan con él, y se llama la
falta de una solución .
No hay muchas maneras de salir de esta situación:
- Puede caerse : este es un método muy común. Quienes trabajan con MacOS saben que NSLayoutConstraintManager hace exactamente eso.
- Devuelve el valor predeterminado . En el contexto del diseño, siempre podemos devolver todos los ceros.
- Una forma más conocida y delicada es evitar la entrada incorrecta . Este método es utilizado por sistemas de diseño populares, por ejemplo, Yoga , conocido como Diseño Flex . Dichos sistemas intentan crear una interfaz que no permita entradas incorrectas.
- Hay otra forma de resolver absolutamente todos los problemas: repensar todo desde el principio e inicialmente para evitar la aparición de este problema . El diseño automático fue de esa manera.
Diseño automático Declaración y solución del problema.
Tenemos una imagen rectangular y para identificarla de manera única, necesitamos 4 parámetros:
- coordenadas de la esquina superior izquierda;
- ancho y alto.
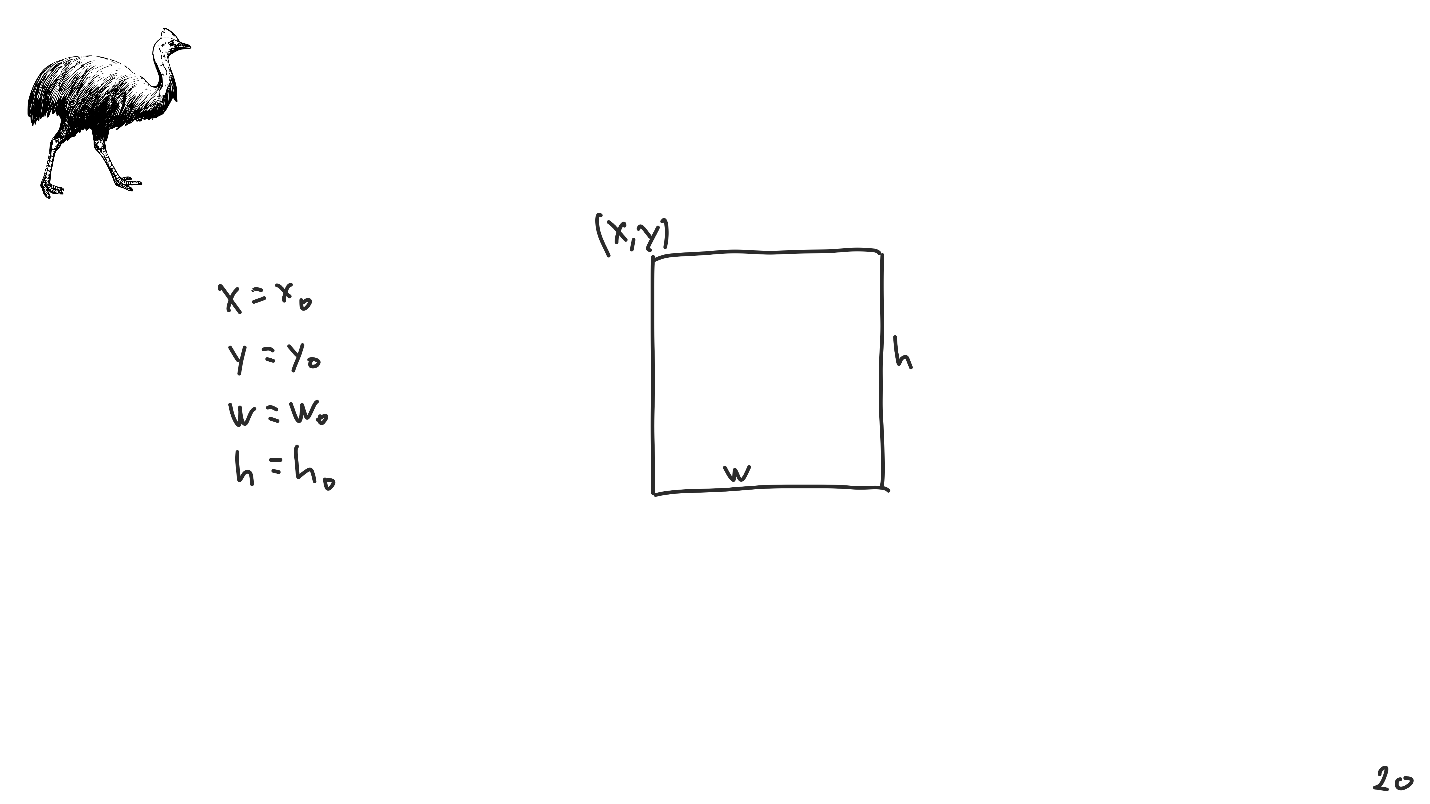
El diseño automático es muy detallado. En comparación con un sistema de ecuaciones lineales, es mucho más difícil colocar todo en la pantalla con él. Por lo tanto, consideraremos, sin pérdida de generalidad, el caso unidimensional.

Todo es muy simple: el espacio es una línea recta, y todos los objetos que se pueden colocar en él son puntos en una línea recta. Un valor:
X = X P es suficiente para determinar la posición del punto.
Considere el enfoque de diseño automático. Hay un espacio en el que se establecen restricciones. La solución que queremos obtener es
X = X 0 , y ninguna otra.
Hay un problema: no hemos definido operaciones con restricciones. No podemos concluir directamente del registro que
X = X 0 , no podemos multiplicar nada ni agregar nada a nada. Para hacer esto, necesitamos transformar la restricción en lo que podemos trabajar, en un sistema de ecuaciones y desigualdades.

El diseño automático transforma un sistema de ecuaciones y desigualdades de la siguiente manera.
- Primero introduce 2 variables adicionales que no son negativas y dependen unas de otras . Al menos uno de ellos es igual a cero.
- La restricción en sí se convierte a la notación X = X 0 + a + - a - .
Punto
X 0 - solución del sistema: si
a + y
a - son iguales a cero, entonces esto será cierto. Pero
cualquier otro punto en esta línea será una solución.
Por lo tanto, es necesario encontrar la mejor entre todas las soluciones. Para hacer esto, presentamos una función funcional, una función ordinaria que devuelve un número, y podemos comparar números. Dibujamos un gráfico y observamos que la solución que originalmente queríamos obtener es mínima.
Tengo
un problema de programación lineal . Esto es exactamente lo que hace el diseño automático con restricciones, que no son solo en forma de igualdades, sino también de desigualdades.
Restricciones de desigualdad
En el caso de las restricciones de desigualdad, la transformación se produce de la misma manera que con las igualdades: se introducen dos variables adicionales y todo esto se recopila en el sistema. Solo lo funcional es diferente, y es igual a
a - .

El gráfico anterior muestra por qué esto es así: cualquier valor de
a + con
a - = 0 (de
X 0 a
+ ∞ ) será la solución óptima para el problema.
Intentemos combinar estas dos restricciones de ecuaciones y desigualdades en una sola, ya que las restricciones no viven de forma aislada, se aplican juntas a todo el sistema.

Para cada restricción, se introduce un par adicional de variables y se compila el funcional. Dado que queremos que todas estas restricciones se cumplan simultáneamente, el
funcional será igual a la suma de todos los funcionales de cada restricción .
Recopilamos la función f y vemos que la solución es
X 1 . Como esperábamos, haciendo restricciones. Entonces llegamos al tercer algoritmo.
Algoritmo No. 3
Para hacer algo, necesitas:
- crear un sistema de restricciones lineales;
- transformarlo en un problema de programación lineal;
- resuelva el problema de cualquier manera conocida, por ejemplo, el método simplex que se usa en Auto Layout;
- aplicar la solución a UIView.
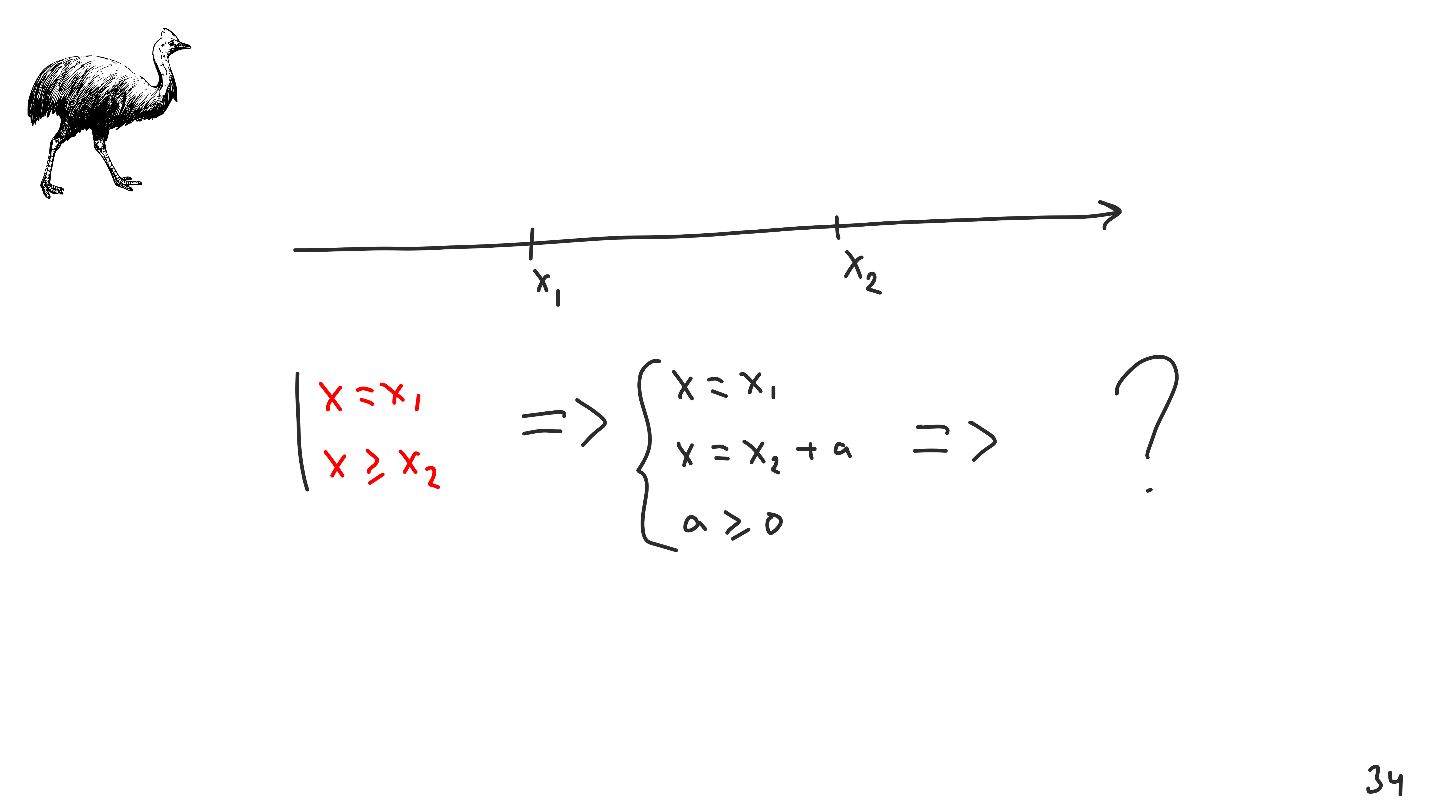
Este algoritmo parece ser suficiente, pero considere el siguiente caso: cambiamos el conjunto inicial de restricciones para que la segunda restricción sea ahora
X ≥ X 2 .

¿Qué solución esperamos ver?
- X 1 ? De hecho, en la primera restricción está escrito así: X = X 1 , y esta solución entra en conflicto con la segunda restricción.
- X 2 ? Ya habrá un conflicto con la primera restricción.
Para salir de la situación, realizaremos transformaciones que ya sabemos cómo hacer.
El gráfico de la nueva funcionalidad se ve diferente: cualquier punto del intervalo de
X 1 a
X 2 será la solución válida correcta del sistema. Esto se llama
incertidumbre .
Incertidumbre
El diseño automático tiene un mecanismo para resolver tales problemas:
prioridades . Les recuerdo que el amarillo indicará alta prioridad y el azul, bajo.
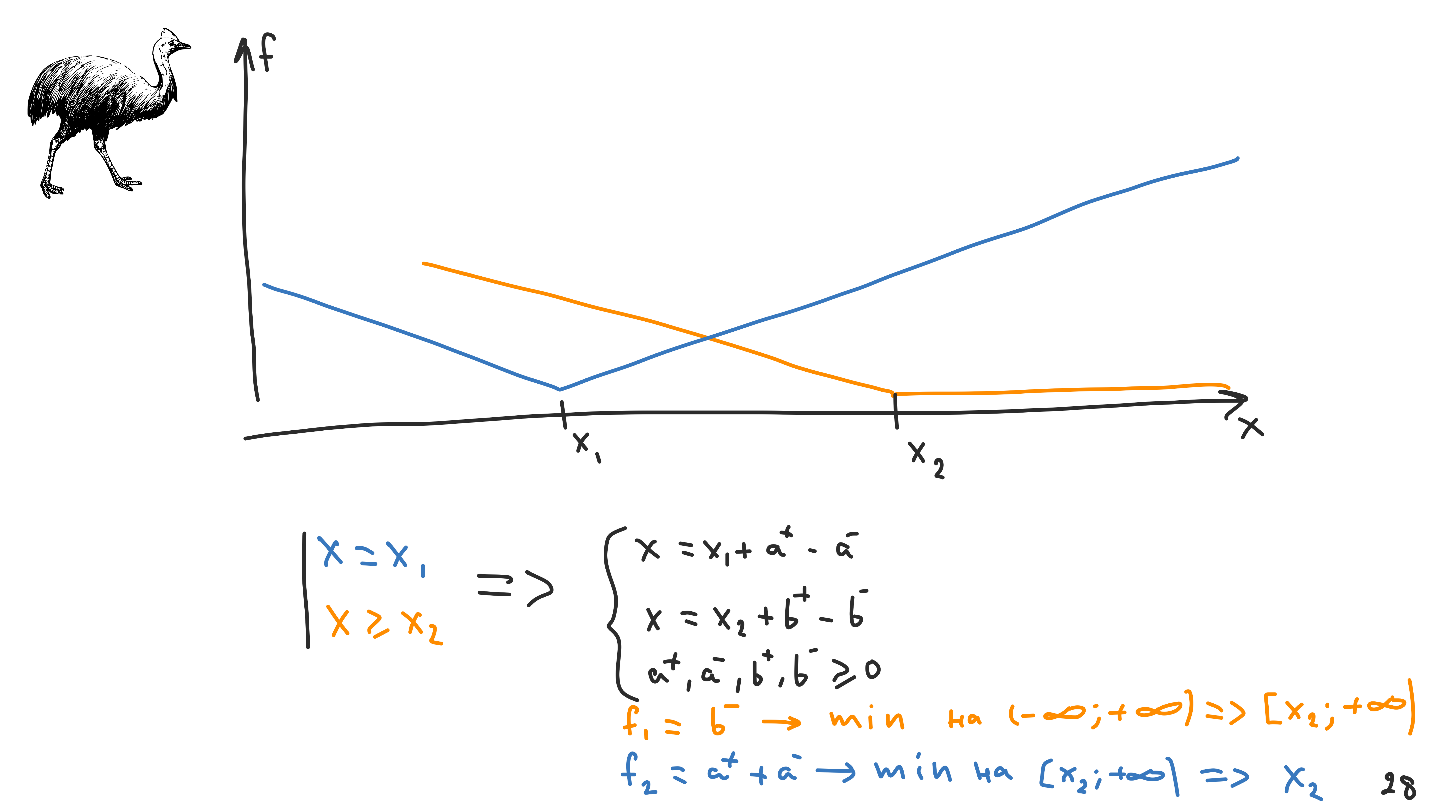
Convertir restricciones. Tenga en cuenta que el sistema resultante es solo negro. Sabemos cómo trabajar con él, y no hay información sobre restricciones en él. Está en las funcionalidades, de las cuales habrá dos. El diseño automático minimizará primero el primero y luego el segundo.
En problemas de programación lineal, no buscamos la solución en sí, sino la gama de soluciones factibles. Por supuesto, queremos que esta área sea solo un punto, y el diseño automático actúa de la misma manera. Primero, minimiza la funcionalidad de mayor prioridad en (
- ∞, + ∞) y, en la salida, recibe un dominio de soluciones factibles. El diseño automático resuelve el segundo problema de programación lineal que ya se encuentra en el rango de valores permitidos obtenido. Tal mecanismo se denomina
jerarquía de restricciones , y en este problema da el punto
X 2 .
Algoritmo No. 4
- Crear una jerarquía de restricciones lineales;
- transformarlo en una tarea de programación lineal;
- resuelva secuencialmente el problema de programación lineal, desde la prioridad más alta hasta la prioridad más baja.
- aplicar la solución a UlView.
Miremos la tarea anterior nuevamente. No somos matemáticos, sino ingenieros, y cualquier ingeniero debería confundirse aquí.
Aquí hay un problema grave: el
infinito , y no sé qué es.
El algoritmo Cassowary bajo el capó del diseño automático no era un mecanismo existente que cayera convenientemente en la tarea de diseño automático, sino que se pensó como una herramienta de diseño, y proporcionó mecanismos especiales para escapar del infinito desde el principio. Para esto, se inventaron varios tipos de restricciones:
- Los parámetros son las restricciones con las que hemos estado trabajando. Se llaman preferencias en el original , a veces en la documentación de Apple, restricciones opcionales .
- Requisitos o requisitos: se requieren restricciones con prioridad.
Veamos cómo se transforman los requisitos con tales prioridades desde el punto de vista de las matemáticas.

Nuevamente tenemos una línea recta con dos puntos, y la primera restricción es
X = X 1 . En la diapositiva, es rojo, es decir, esta restricción con la prioridad requerida: la llamaremos un requisito.
El diseño automático lo convierte en un sistema de ecuaciones lineales que contiene una ecuación
X = X 1 . Nada más: sin tareas de programación lineal, sin optimizaciones.
La situación es similar con las desigualdades, pero un poco más complicada: aparecerá
una variable adicional que puede tomar cualquier valor mayor que 0. Para cualquier valor mayor que 0, esta restricción se cumplirá. Tenga en cuenta que aquí no hay tareas de programación lineal y optimizaciones.
Intentemos combinar todo esto, juntar dos requisitos y convertirlos en un solo sistema. Un lector atento, señaló que llegamos al mismo problema con el que comenzamos: los
requisitos deben ser consistentes .
Las restricciones de tipo
requeridas o requisitos son una
herramienta muy poderosa, pero no la principal, sino la auxiliar. Se introdujo especialmente en Auto Layout para resolver el problema de los intervalos infinitos, debe usarse con cuidado.
Intentemos combinar todos los tipos de restricciones que encontramos en un sistema. Supongamos que queremos resolver el problema no en toda la línea, sino solo entre
X 0 y
X 3 . Transformando todo esto en un sistema de ecuaciones lineales y desigualdades, obtenemos lo siguiente.
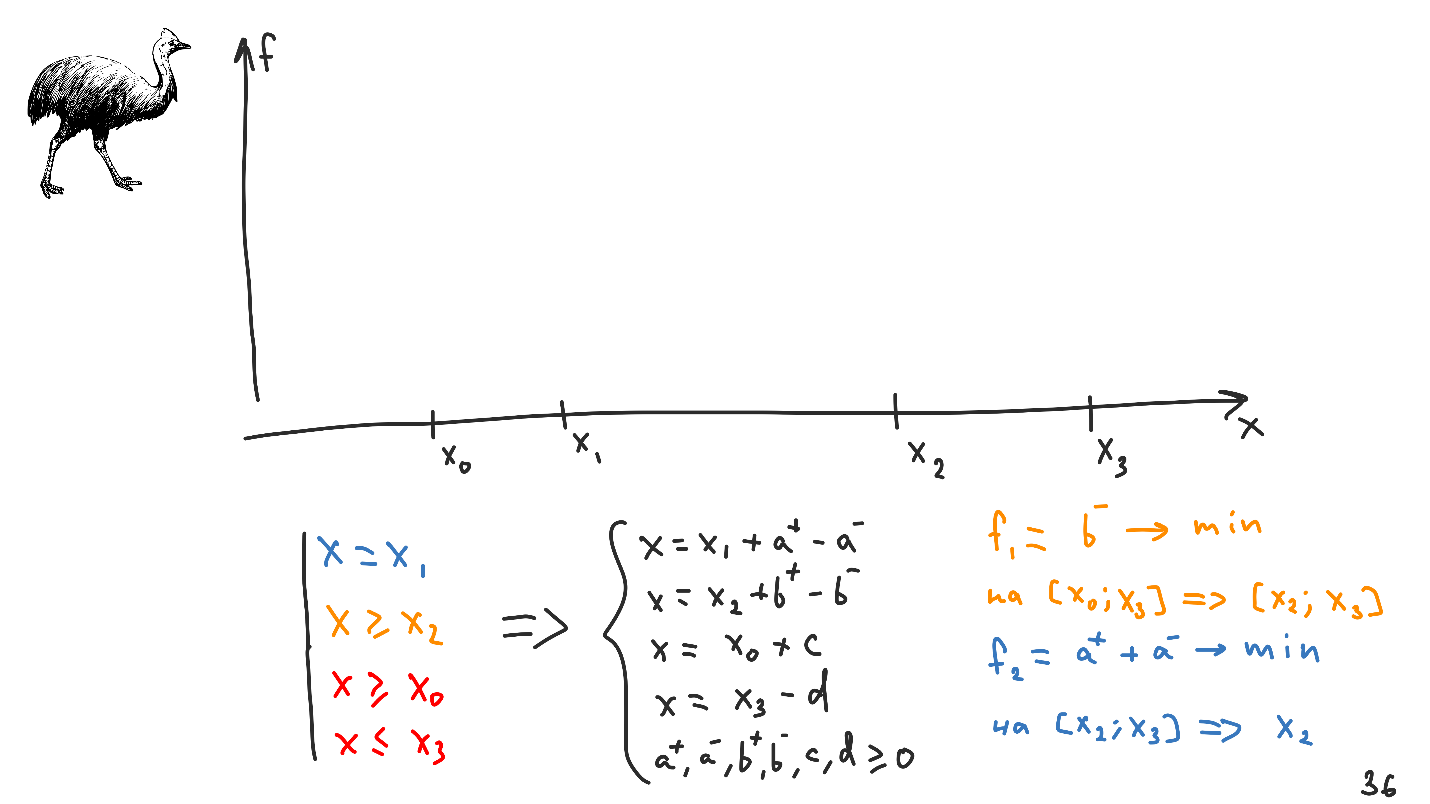
En relación con el sistema anterior, se agregaron dos variables adicionales:
cyd , pero no entrarán en los funcionales, ya que las restricciones del tipo requerido no afectan al funcional en su forma original.
Parece que la tarea no ha cambiado mucho: minimizamos lo mismo que antes, pero el rango inicial de valores aceptables está cambiando, ahora es de
X 0 a
X 3 .
Desde un punto de vista matemático, los requisitos (restricciones del tipo requerido) son la capacidad de introducir ecuaciones adicionales en el sistema sin modificar sus funciones.
Debe tener mucho cuidado con esto, porque el abuso excesivo de las restricciones requeridas conducirá a un
problema sin soluciones , y el diseño automático
no lo resolverá .
Llegamos al último quinto algoritmo.
Algoritmo No. 5
- Definir las restricciones necesarias: requisitos de diseño;
- crear una jerarquía de restricciones lineales;
- convertir todas las restricciones en un problema de programación lineal;
- resolver el problema de la programación lineal;
- aplicar la solución a UlView.
Examinamos Cassowary, un algoritmo que está dentro del diseño automático, pero cuando se implementa, surgen varias características.
Características del IOS
No hay cálculos en layoutSubviews () .
¿Cuándo se producen? Respuesta: siempre, en cualquier momento, se cuenta el diseño automático. El cálculo ocurre exactamente cuando agregamos restricciones a nuestra vista, o las activamos usando métodos API modernos para trabajar con restricciones.
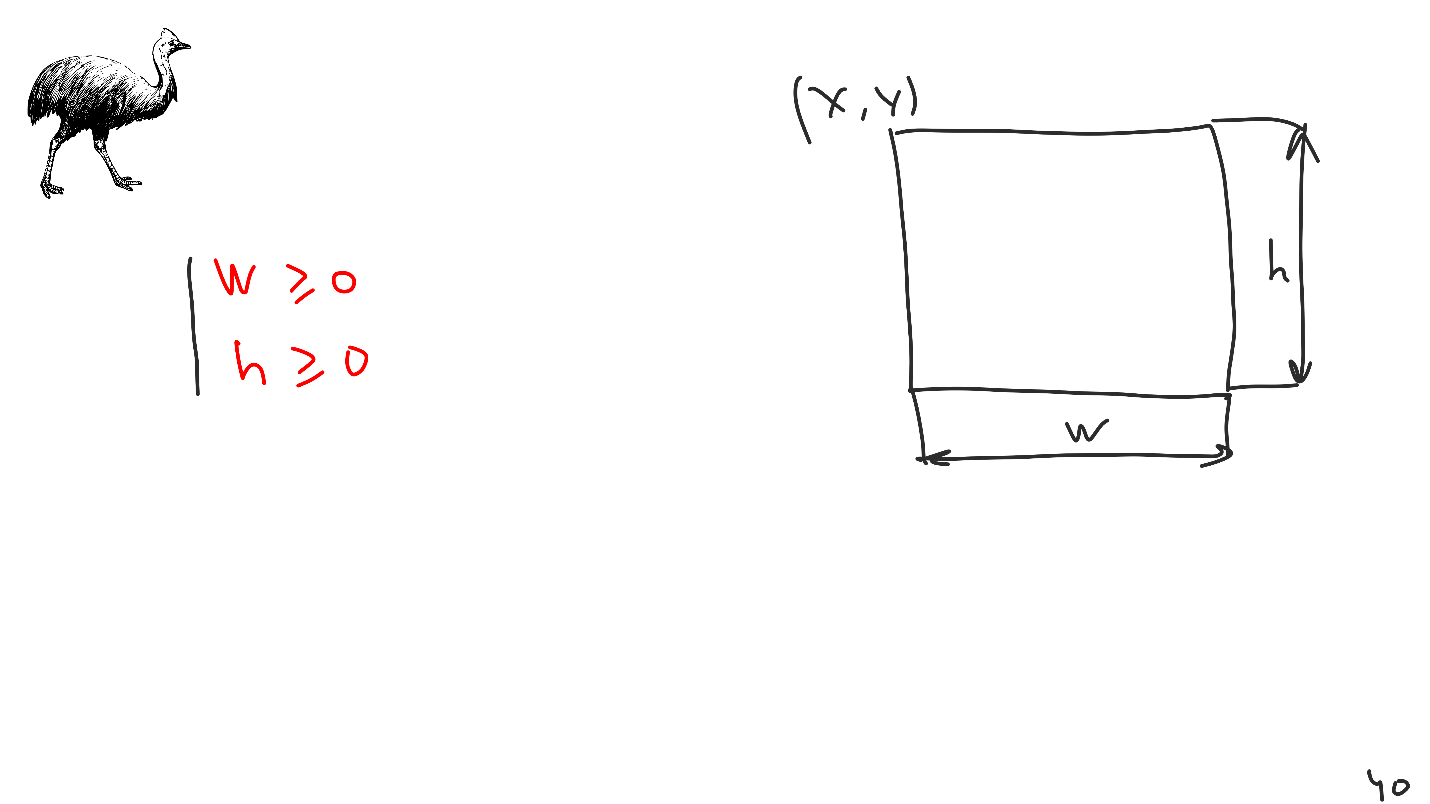
Nuestras vistas son rectángulos, pero el problema es que esta información no está contenida dentro del Cassowary, sino que también debe incrustarse allí. Tenemos un mecanismo para introducir restricciones adicionales. Si introducimos para cada vista un conjunto de restricciones con ancho y alto positivos, entonces siempre obtendremos rectángulos en la salida. Es por eso que no podemos hacer las paces con la vista Diseño automático con dimensiones negativas.
La segunda característica es
intrinsicContentSize : el tamaño intrínseco que se puede establecer para cada vista.
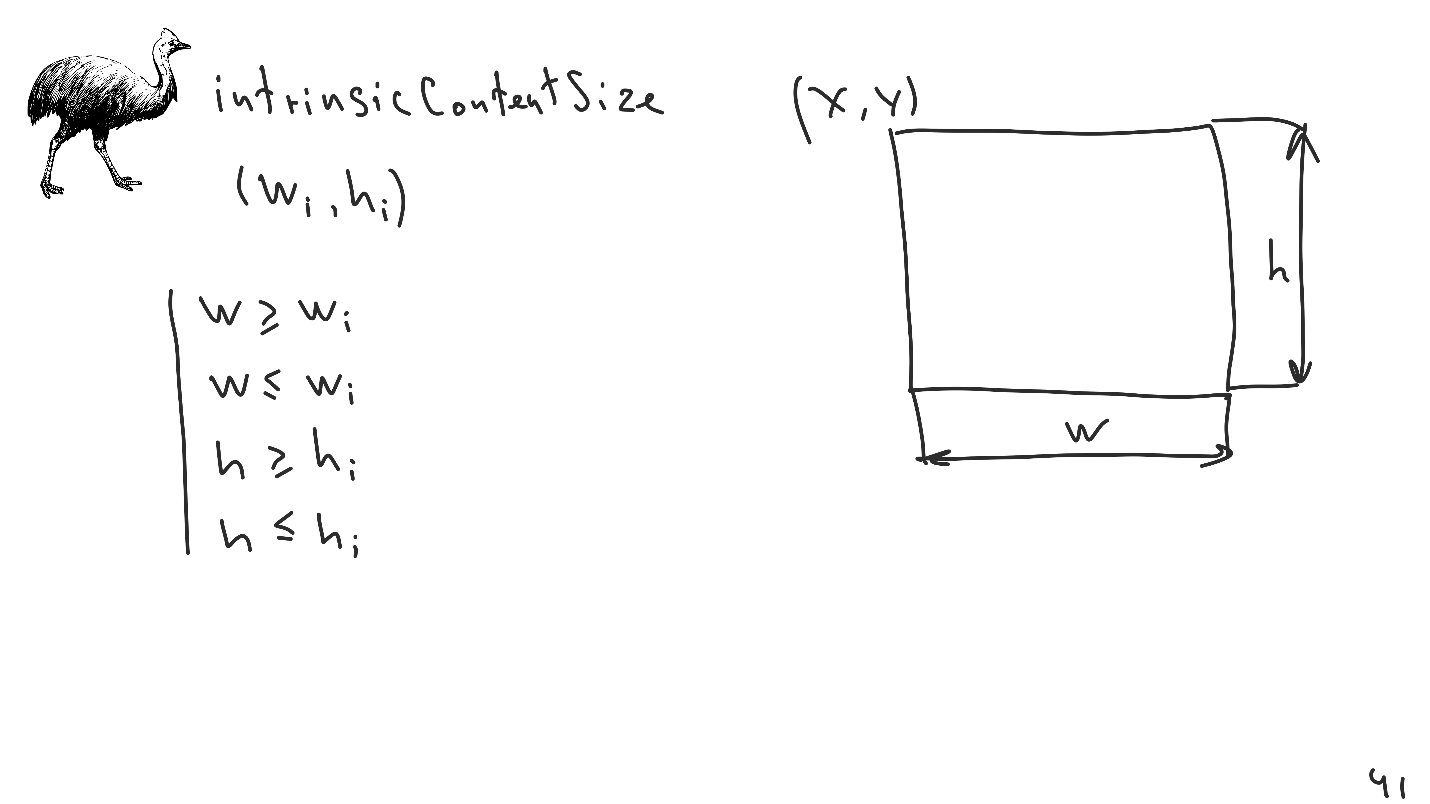
Esta es una interfaz simple para crear 4 restricciones de desigualdad adicionales que se colocarán en el sistema. Este mecanismo es muy conveniente, le permite reducir el número de restricciones explícitas, lo que simplifica el uso del diseño automático. El último y más delgado punto que a menudo se olvida es
TranslateAutoresizingMaskIntoConstraints.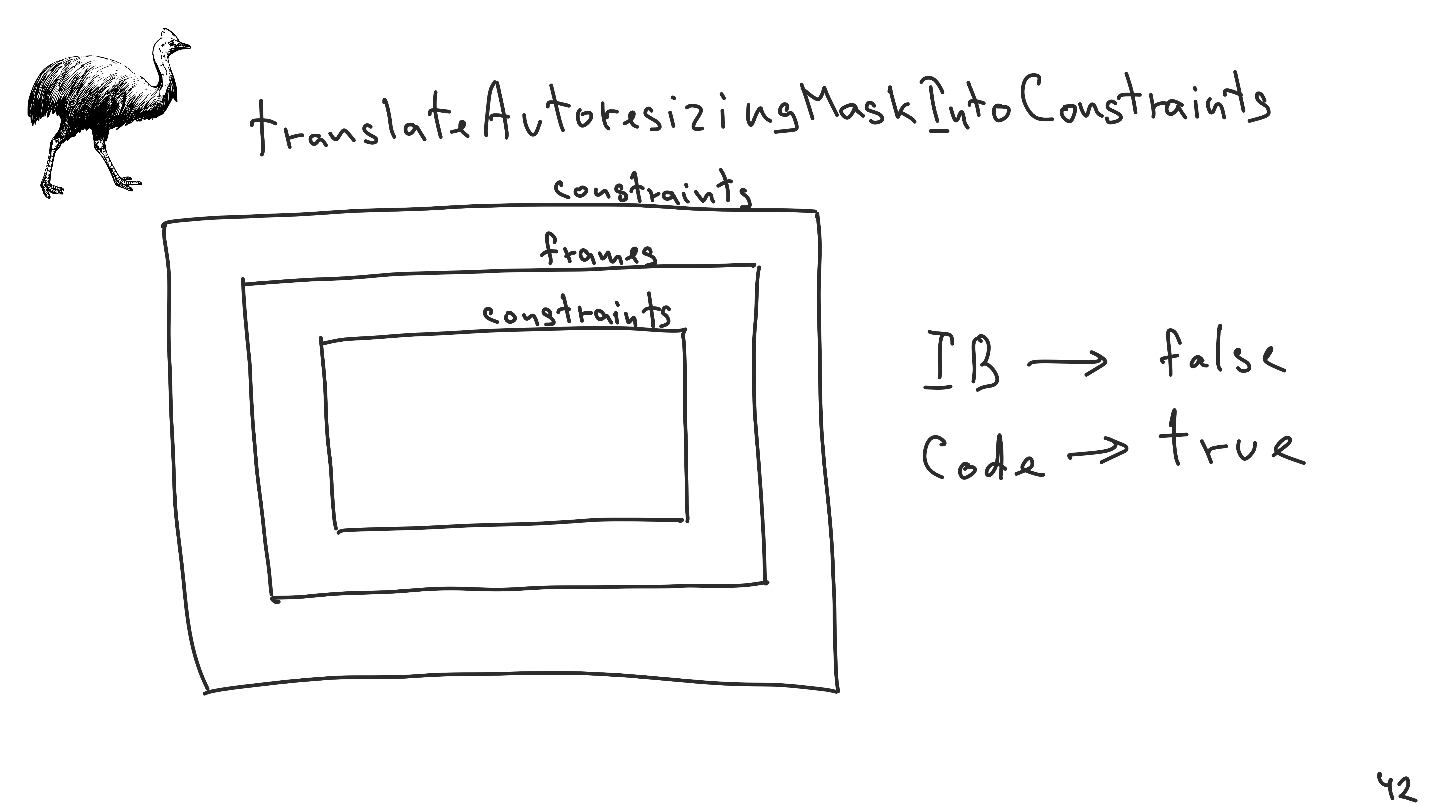
Esta es una
muleta que se introdujo en los días de iOS 5, para que el código anterior no se rompa después de la aparición de Auto Layout.
Imagine una situación: imponemos una visión sobre las restricciones. Dentro de la vista, usamos la vista, que no sabe nada acerca de las restricciones, todo se compone en marcos, pero dentro de ella escribe la vista, que durante mucho tiempo se ha traducido en restricciones.
Les recuerdo que no hay marcos en la tarea de diseño automático de Cassowary, solo limitaciones.
El tamaño y la posición de la vista que se contrajo en los marcos no están completamente determinados por restricciones. Al calcular el tamaño y la posición de todas las demás vistas, se tendrán en cuenta los tamaños incorrectos, aunque después del diseño automático aplicaremos los marcos correctos allí.
Para evitar esta situación, si el valor de la variable TranslateAutoresizingMaskIntoConstraints es verdadero, se aplica una restricción adicional a cada vista que se presenta en el marco. Este conjunto de restricciones puede variar de una ejecución a otra. Solo se sabe una cosa sobre este conjunto: su trama será la que se transmitió.
La compatibilidad entre el código antiguo escrito sin restricciones y el nuevo código escrito con restricciones a menudo puede verse afectado por el mal uso de esta propiedad. Estas restricciones necesariamente tienen la prioridad de los requisitos, por lo que si de repente imponemos una restricción a dicha vista, que tiene una prioridad muy alta, por ejemplo, un requisito, podemos crear accidentalmente un sistema no consistente que no tendrá soluciones.
Es importante saber:- Si creamos una vista desde Interface Builder , el valor predeterminado para esta propiedad será falso .
- Si creamos una vista directamente desde el código, entonces será cierto .
La idea es muy simple: el antiguo código en el que se creó la vista no sabía nada sobre el diseño automático, y era necesario hacerlo para que, si la vista se usara en algún lugar de un lugar nuevo, funcionara.
Consejos prácticos
Habrá tres consejos en total y comenzará con el más importante.
Optimización
Es importante localizar el problema.
¿Alguna vez ha enfrentado el problema de optimizar la pantalla, que se presenta en Diseño automático? Lo más probable es que no, con mayor frecuencia se ha enfrentado al problema de optimizar el diseño de las celdas dentro de una tabla o una
Vista de colección .
El diseño automático está lo suficientemente optimizado para crear cualquier pantalla y cualquier interfaz, pero crear 50 o 100 a la vez es un problema. Para localizarlo y optimizarlo, veamos el experimento. Las cifras están tomadas de un
artículo donde se describió por primera vez Cassowary.

La tarea es esta: creamos una cadena de vista una por una, y conectamos cada una de ellas con la anterior. Por lo tanto, se construyó una secuencia de 1000 elementos. Después de medir varias operaciones, el tiempo se indica en milisegundos. Los valores son bastante grandes, porque el diseño automático se inventó en la unión de los años 80 y 90.
Al recopilar dicha cadena, puede actuar de la siguiente manera:
- Agregue restricción de una en una y decida cada vez. Esto llevará 38 segundos.
- Puede agregar todas las restricciones a la vez , y solo luego resolver el sistema. Esta solución es más eficiente. Según datos antiguos, la eficiencia aumenta en un 70%, pero en la implementación actual en dispositivos modernos solo habrá un 20%. Pero una adición cualitativa cualitativa de restricciones siempre será más efectiva.
- Cuando se ensambla toda la cadena, puede agregar una restricción más . Como se puede ver en la tabla, esta operación es bastante barata.
- Lo más interesante: si no agregamos ninguna restricción nueva, pero cambiamos alguna constante en una de las existentes , este es un orden de magnitud más efectivo que eliminar o crear una nueva restricción.
Los primeros dos puntos pueden describirse como el cálculo primario de las interfaces, los dos últimos, como el siguiente.
Cálculo de interfaz primaria
Aquí puede utilizar los métodos de agregar restricciones de forma masiva para la optimización:
- NSLayoutConstraints.activate (_ :) : al crear una vista, recopile todas las restricciones secuencialmente en una matriz, caché y solo luego agréguela a la vez.
- O cree celdas en Interface Builder. Hará todo por nosotros y llevará a cabo una optimización adicional, que a menudo es conveniente.
Cálculos posteriores de la interfaz
Agregar o modificar restricciones es una operación compleja, por lo que es mejor
no cambiar el conjunto de restricciones, sino solo cambiar las constantes en las restricciones existentes. :
- UIView — . view , Auto Layout. , , view, .
- — IntrinsicContentSize. , , .
- . , , .
,
WWDC 2018S220 High Performance Auto Layout . — Apple , .
, constraints.
required , — , , . .
, .
:
, , .
constraint required, . , , , . , .
—
, . , — . - , , . Auto Layout , .
, . . , , , . layout, , , . .
— , Auto Layout, , .
, required, ,
. :
, ,
, .
, . , , , . ,
— . .
— . , , , — , — required -.
:Solving Linear Arithmetic Constraints for User Interface ApplicationsThe Cassowary Linear Constraint Solving AlgorithmConstraints as s Design PatternAuto Layout Guide by AppleWWDC 2018 Session 220 High Performance Auto LayoutUILabel API Auto Layout —. MediumPor cierto, ya hemos aceptado el informe de Anton en el programa AppsConf 2019 . Permítanme recordarles que cambiamos AppsConf de otoño a primavera, y la próxima conferencia más útil para desarrolladores móviles se llevará a cabo los días 22 y 23 de abril. Es hora de pensar en el tema para la presentación y presentar un informe , o discutir con el líder la importancia de ir a la conferencia y reservar un boleto.