Introduccion

Hablando de técnicas de programación específicas para OSG , la última vez que hablamos sobre el mecanismo de devolución de llamada y su implementación en el motor. Es hora de ver las posibilidades que ofrece este mecanismo para administrar el contenido de una escena tridimensional.

Si hablamos de animación de objetos, OSG proporciona al desarrollador dos opciones para su implementación:

1. Animación procesal implementada programáticamente a través de la transformación de objetos y sus atributos.
2. Exportar animación desde un editor 3D y administrarla desde el código de la aplicación

Para comenzar, considere la primera posibilidad, como la más obvia. Definitivamente hablaremos sobre el segundo un poco más tarde.

1. Animación de transformación procesal

Al atravesar el gráfico de escena, OSG transfiere datos a la canalización de OpenGL, que se ejecuta en un hilo separado. Este hilo debe estar sincronizado con otros hilos de procesamiento en cada cuadro. De lo contrario, el método frame () puede completarse antes de procesar los datos de geometría. Esto conducirá a comportamientos y bloqueos impredecibles del programa. OSG ofrece una solución a este problema en forma del método setDataVariance () de la clase osg :: Object, que es la base para todos los objetos de escena. Puede configurar tres modos de procesamiento para objetos

1. NO ESPECIFICADO (por defecto): OSG determina independientemente el orden de procesamiento del objeto.
   
2. ESTÁTICO: el objeto es inmutable y el orden de su procesamiento no es importante. Acelera significativamente el renderizado.
   
3. DINÁMICO: el objeto debe procesarse antes del inicio de la representación.
   

Esta configuración se puede establecer en cualquier momento llamando

node->setDataVariance( osg::Object::DYNAMIC ); 

La práctica generalmente aceptada es modificar la geometría "sobre la marcha", es decir, cambiar las coordenadas de vértices, colores normales y texturas dinámicamente en cada cuadro, obteniendo geometría mutable. Esta técnica se llama animación de transformación. En este caso, el orden de procesamiento de la geometría es decisivo: todos sus cambios deben recalcularse antes de que comience el dibujo. Para ilustrar este truco, modificamos ligeramente el ejemplo cuadrado de color, obligando a uno de sus vértices a girar alrededor del eje X.


Crearemos un cuadrado en una función separada

 osg::Geometry *createQuad() { osg::ref_ptr<osg::Vec3Array> vertices = new osg::Vec3Array; vertices->push_back( osg::Vec3(0.0f, 0.0f, 0.0f) ); vertices->push_back( osg::Vec3(1.0f, 0.0f, 0.0f) ); vertices->push_back( osg::Vec3(1.0f, 0.0f, 1.0f) ); vertices->push_back( osg::Vec3(0.0f, 0.0f, 1.0f) ); osg::ref_ptr<osg::Vec3Array> normals = new osg::Vec3Array; normals->push_back( osg::Vec3(0.0f, -1.0f, 0.0f) ); osg::ref_ptr<osg::Vec4Array> colors = new osg::Vec4Array; colors->push_back( osg::Vec4(1.0f, 0.0f, 0.0f, 1.0f) ); colors->push_back( osg::Vec4(0.0f, 1.0f, 0.0f, 1.0f) ); colors->push_back( osg::Vec4(0.0f, 0.0f, 1.0f, 1.0f) ); colors->push_back( osg::Vec4(1.0f, 1.0f, 1.0f, 1.0f) ); osg::ref_ptr<osg::Geometry> quad = new osg::Geometry; quad->setVertexArray(vertices.get()); quad->setNormalArray(normals.get()); quad->setNormalBinding(osg::Geometry::BIND_OVERALL); quad->setColorArray(colors.get()); quad->setColorBinding(osg::Geometry::BIND_PER_VERTEX); quad->addPrimitiveSet(new osg::DrawArrays(GL_QUADS, 0, 4)); return quad.release(); } 

una descripción de la cual, en principio, no es necesaria, ya que hemos realizado tales acciones repetidamente. Para modificar los vértices de este cuadrado, escribimos la clase DynamicQuadCallback, heredando de osg :: Drawable :: UpdateCallback

 class DynamicQuadCallback : public osg::Drawable::UpdateCallback { public: virtual void update(osg::NodeVisitor *, osg::Drawable *drawable); }; 

anulando el método update () en él

 void DynamicQuadCallback::update(osg::NodeVisitor *, osg::Drawable *drawable) { osg::Geometry *quad = static_cast<osg::Geometry *>(drawable); if (!quad) return; osg::Vec3Array *vertices = static_cast<osg::Vec3Array *>(quad->getVertexArray()); if (!vertices) return; osg::Quat quat(osg::PI * 0.01, osg::X_AXIS); vertices->back() = quat * vertices->back(); quad->dirtyDisplayList(); quad->dirtyBound(); } 

Aquí obtenemos un puntero a un objeto de geometría

 osg::Geometry *quad = static_cast<osg::Geometry *>(drawable); 

leemos de la geometría una lista de vértices (o más bien un puntero a ella)

 osg::Vec3Array *vertices = static_cast<osg::Vec3Array *>(quad->getVertexArray()); 

Para obtener el último elemento (último vértice) en la matriz, la clase osg :: Array proporciona el método back (). Para rotar el vértice en relación con el eje X, presentamos

 osg::Quat quat(osg::PI * 0.01, osg::X_AXIS); 

es decir, establecemos un cuaternión que implementa una rotación alrededor del eje X en un ángulo de 0.01 * Pi. Gire el vértice multiplicando el cuaternión por un vector que defina las coordenadas del vértice

 vertices->back() = quat * vertices->back(); 

Las últimas dos llamadas relatan la lista de visualización y el paralelepípedo dimensional para la geometría modificada.

 quad->dirtyDisplayList(); quad->dirtyBound(); 

En el cuerpo de la función main (), creamos un cuadrado, establecemos el modo de dibujo dinámico para él y agregamos una devolución de llamada modificando la geometría

 osg::Geometry *quad = createQuad(); quad->setDataVariance(osg::Object::DYNAMIC); quad->setUpdateCallback(new DynamicQuadCallback); 

Dejaré indiscriminadamente la creación del nodo raíz y el lanzamiento del visor, ya que ya lo hemos hecho al menos veinte veces de diferentes maneras. Como resultado, tenemos la animación de transformación más simple



Ahora intente eliminar (comentar) la llamada setDataVariance (). Quizás no veamos nada criminal en este caso: de forma predeterminada, OSG intenta determinar automáticamente cuándo actualizar los datos de geometría, tratando de sincronizar con el renderizado. Luego intente cambiar el modo de DINÁMICO a ESTÁTICO y verá que la imagen no se procesa sin problemas, con sacudidas, errores y advertencias notables como esta

 Warning: detected OpenGL error 'invalid value' at after RenderBin::draw(..) 

Si no ejecuta el método dirtyDisplayList (), OpenGL ignorará todos los cambios en la geometría y utilizará la lista de visualización creada al principio para crear el cuadrado para la representación. Elimine esta llamada y verá que no hay animación.

Sin llamar al método dirtyBound (), el cuadro delimitador no se volverá a calcular y OSG recortará incorrectamente las caras invisibles.

2. El concepto de interpolación de movimiento.

Suponga que un tren que va de la estación A a la estación B tarda 15 minutos en viajar. ¿Cómo podemos simular esta situación cambiando la posición del tren en la devolución de llamada? La forma más fácil es correlacionar la posición de la estación A con el tiempo 0 y la estación B con 15 minutos y mover el tren de manera uniforme entre estos tiempos. Este enfoque más simple se llama interpolación lineal. En la interpolación lineal, la fórmula describe un vector que especifica la posición de un punto intermedio

 p = (1 - t) * p0 + t * p1 

donde p0 es el punto de partida; p1 es el punto final; t es un parámetro que varía uniformemente de 0 a 1. Sin embargo, el movimiento del tren es mucho más complicado: sale de la estación A, acelera, luego se mueve a una velocidad constante y luego disminuye la velocidad, deteniéndose en la estación B. Tal proceso ya no puede describir la interpolación lineal y Se ve antinatural.

OSG proporciona al desarrollador la biblioteca osgAnimation, que contiene varios algoritmos de interpolación estándar utilizados para animar sin problemas el movimiento de los objetos de la escena. Cada una de estas funciones generalmente tiene dos argumentos: el valor inicial del parámetro (generalmente 0) y el valor final del parámetro (generalmente 1). Estas funciones se pueden aplicar al inicio del movimiento (InMotion), al final del movimiento (OutMotion) o al inicio y al final del movimiento (InOutMotion)

Tipo de movimiento	en clase	fuera de clase	clase de entrada / salida
Interpolación lineal	Movimiento lineal	-	-
Interpolación cuadrática	InQuadMotion	OutQuadMotion	InOutQuadMotion
Interpolación cúbica	InCubicMotion	Outcubicmotion	InOutCubicMotion
Interpolación de 4 órdenes	InQuartMotion	OutQuartMotion	InOutQuartMotion
Interpolación de efecto de rebote	InBounceMotion	OutBounceMotion	InOutBounceMotion
Interpolación de rebote elástico	InElasticMotion	OutElasticMotion	InOutElasticMotion
Interpolación sinusoidal	InSineMotion	Outsinemotion	InOutSineMotion
Interpolación inversa	Inbackmotion	Outbackmotion	InOutBackMotion
Interpolación circular	InCircMotion	Movimiento exterior	InOutCircMotion
Interpolación exponencial	InExpoMotion	Outexpomotion	InOutExpoMotion

Para crear una interpolación lineal del movimiento de un objeto, escribimos dicho código

 osg::ref_ptr<osgAnimation::LinearMotion> motion = new osgAnimation::LinearMotion(0.0f, 1.0f); 

3. Animación de nodos de transformación.

La animación de trayectoria es el tipo de animación más común en aplicaciones gráficas. Esta técnica se puede utilizar para animar el movimiento de un automóvil, el vuelo de un avión o el movimiento de la cámara. La trayectoria está predefinida, con todas las posiciones, rotaciones y cambios de escala en puntos clave en el tiempo. Cuando comienza el ciclo de simulación, el estado del objeto se recalcula en cada cuadro, utilizando la interpolación lineal para la posición y la escala y la interpolación lineal esférica para los cuaterniones de rotación. Para hacer esto, use el método interno slerp () de la clase osg :: Quat.

OSG proporciona la clase osg :: AnimationPath para describir una ruta que varía en el tiempo. El método de esta clase insert () se usa para agregar puntos de control correspondientes a ciertos puntos en el tiempo a la trayectoria. El punto de control es descrito por la clase osg :: AnimationPath :: ControlPoint, cuyo constructor toma la posición como parámetros y, opcionalmente, la rotación de objetos y los parámetros de escala. Por ejemplo

 osg::ref_ptr<osg::AnimationPath> path = new osg::AnimationPath; path->insert(t1, osg::AnimationPath::ControlPoint(pos1, rot1, scale1)); path->insert(t2, ...); 

Aquí t1, t2 son instantes de tiempo en segundos; rot1 es el parámetro de rotación en el tiempo t1, descrito por el cuaternión osg :: Quat.

Es posible controlar los bucles de animación a través del método setLoopMode (). De manera predeterminada, el modo LOOP está activado: la animación se repetirá continuamente. Otros valores posibles: NO_LOOPING - reproduce la animación una vez y SWING - repite el movimiento en las direcciones hacia adelante y hacia atrás.

Después de completar toda la inicialización, adjuntamos el objeto osg :: AnimationPath al objeto incorporado osg :: AnimationPathCallback, que se deriva de la clase osg :: NodeCallback.

4. Un ejemplo de una animación de movimiento a lo largo de un camino.

Ahora haremos que nuestro cessna se mueva en círculo con el centro en el punto (0,0,0). La posición de la aeronave en la trayectoria se calculará interpolando linealmente la posición y orientación entre cuadros clave.


Comenzamos creando la trayectoria del avión, tomando este código en una función separada

 osg::AnimationPath *createAnimationPath(double radius, double time) { osg::ref_ptr<osg::AnimationPath> path = new osg::AnimationPath; path->setLoopMode(osg::AnimationPath::LOOP); unsigned int numSamples = 32; double delta_yaw = 2.0 * osg::PI / (static_cast<double>(numSamples) - 1.0); double delta_time = time / static_cast<double>(numSamples); for (unsigned int i = 0; i < numSamples; ++i) { double yaw = delta_yaw * i; osg::Vec3d pos(radius * sin(yaw), radius * cos(yaw), 0.0); osg::Quat rot(-yaw, osg::Z_AXIS); path->insert(delta_time * i, osg::AnimationPath::ControlPoint(pos, rot)); } return path.release(); } 

Como parámetros, la función toma el radio del círculo a lo largo del cual se mueve el avión y el tiempo durante el cual hará una revolución. Dentro de la función, cree un objeto de trayectoria y active el modo de bucle de animación

 osg::ref_ptr<osg::AnimationPath> path = new osg::AnimationPath; path->setLoopMode(osg::AnimationPath::LOOP); 

Código siguiente

 unsigned int numSamples = 32; double delta_yaw = 2.0 * osg::PI / (static_cast<double>(numSamples) - 1.0); double delta_time = time / static_cast<double>(numSamples); 

calcula los parámetros de aproximación de la trayectoria. Dividimos toda la trayectoria en numSamples de secciones rectas, y calculamos el cambio en el ángulo de rotación del plano alrededor del eje vertical (yaw) delta_yaw y el cambio en el tiempo delta_time cuando se mueve de una sección a otra. Ahora crea los puntos de control necesarios

 for (unsigned int i = 0; i < numSamples; ++i) { double yaw = delta_yaw * i; osg::Vec3d pos(radius * sin(yaw), radius * cos(yaw), 0.0); osg::Quat rot(-yaw, osg::Z_AXIS); path->insert(delta_time * i, osg::AnimationPath::ControlPoint(pos, rot)); } 

En el ciclo, se ordenan todas las secciones de la trayectoria, desde la primera hasta la última. Cada punto de control se caracteriza por un ángulo de guiñada

 double yaw = delta_yaw * i; 

la posición del centro de masa de la aeronave en el espacio

 osg::Vec3d pos(radius * sin(yaw), radius * cos(yaw), 0.0); 

El cuaternión establece la rotación de la aeronave al ángulo de guiñada deseado (en relación con el eje vertical)

 osg::Quat rot(-yaw, osg::Z_AXIS); 

y luego agregue los parámetros calculados a la lista de puntos de control de la ruta

 path->insert(delta_time * i, osg::AnimationPath::ControlPoint(pos, rot)); 

En el programa principal, prestamos atención al matiz al indicar el nombre del archivo de modelo de la aeronave al momento del arranque

 osg::ref_ptr<osg::Node> model = osgDB::readNodeFile("../data/cessna.osg.0,0,90.rot"); 

- se agregó un sufijo ".0,0,90.rot" al nombre del archivo. El mecanismo para cargar geometría desde un archivo utilizado en OSG le permite especificar la posición inicial y la orientación del modelo después de la carga. En este caso, queremos que el modelo gire 90 grados alrededor del eje Z después de cargarlo.

A continuación, se crea el nodo raíz, que es el nodo de transformación, y el objeto modelo se agrega como un nodo secundario

 osg::ref_ptr<osg::MatrixTransform> root = new osg::MatrixTransform; root->addChild(model.get()); 

Ahora cree una devolución de llamada de animación de trayectoria, agregando la ruta creada por la función createAnimationPath ()

 osg::ref_ptr<osg::AnimationPathCallback> apcb = new osg::AnimationPathCallback; apcb->setAnimationPath(createAnimationPath(50.0, 6.0)); 

Adjunte esta devolución de llamada al nodo de transformación

 root->setUpdateCallback(apcb.get()); 

El visor se inicializa y se inicia como de costumbre.

 osgViewer::Viewer viewer; viewer.setSceneData(root.get()); return viewer.run(); 

Obtén una animación de movimiento de avión



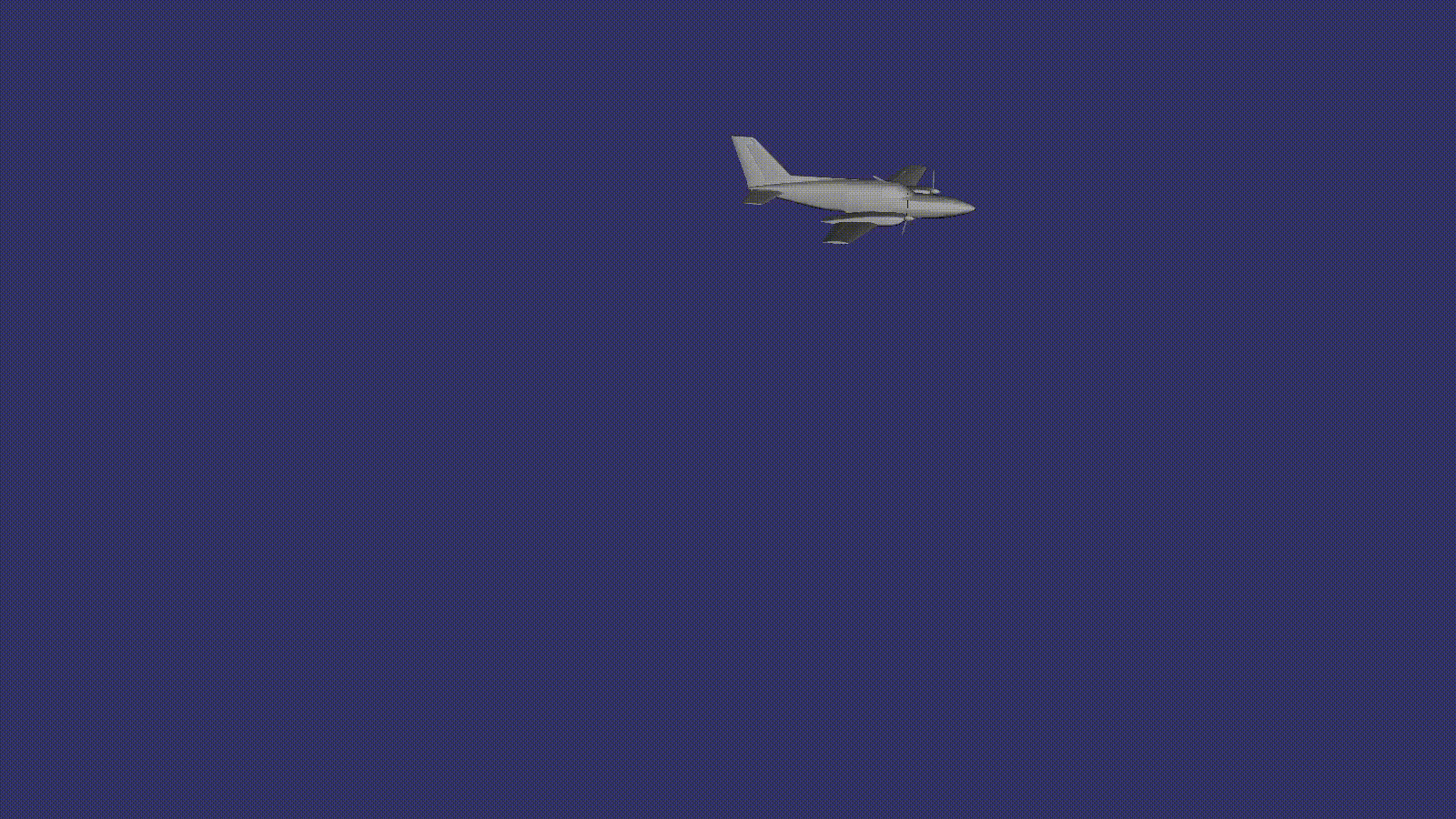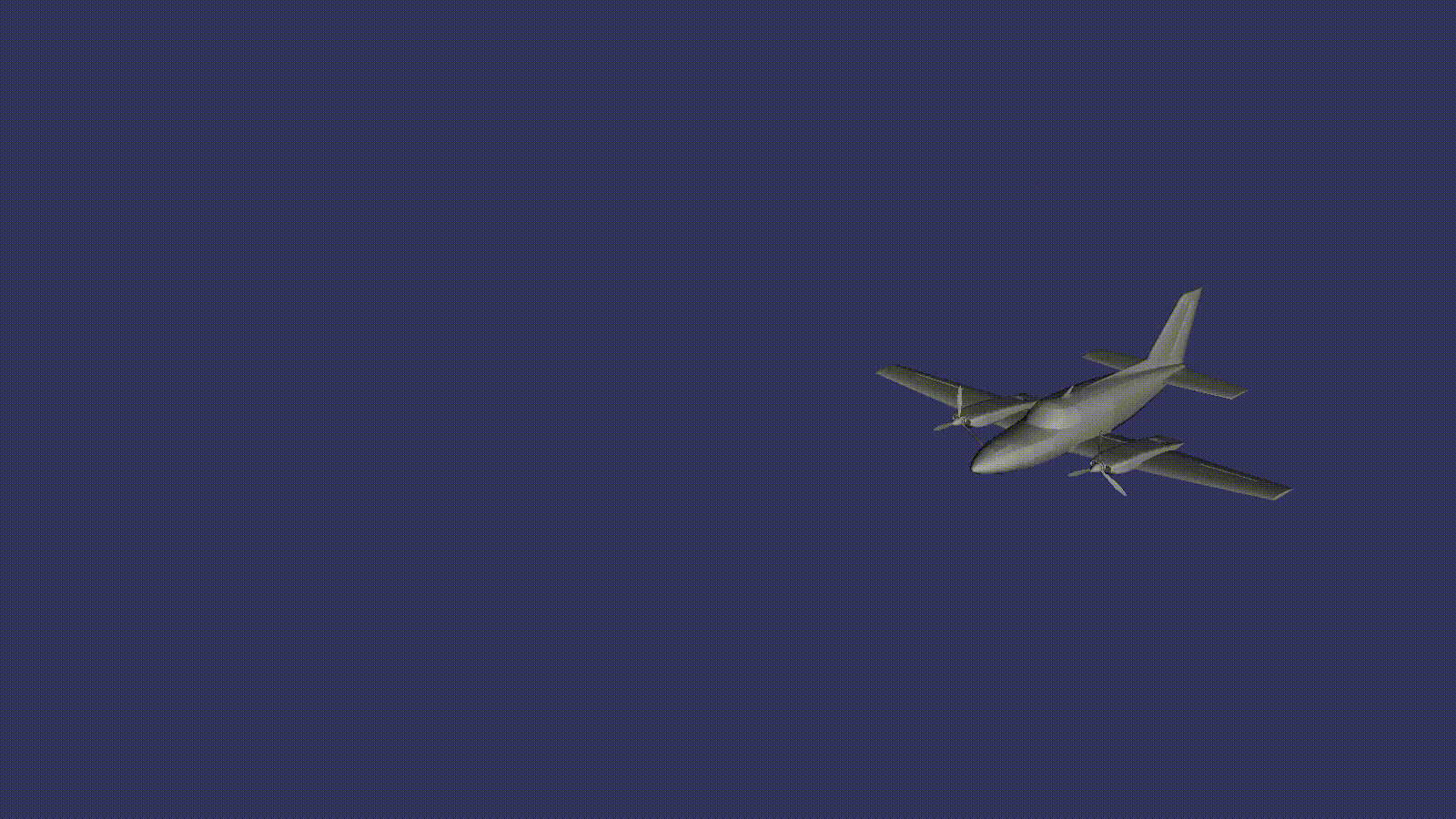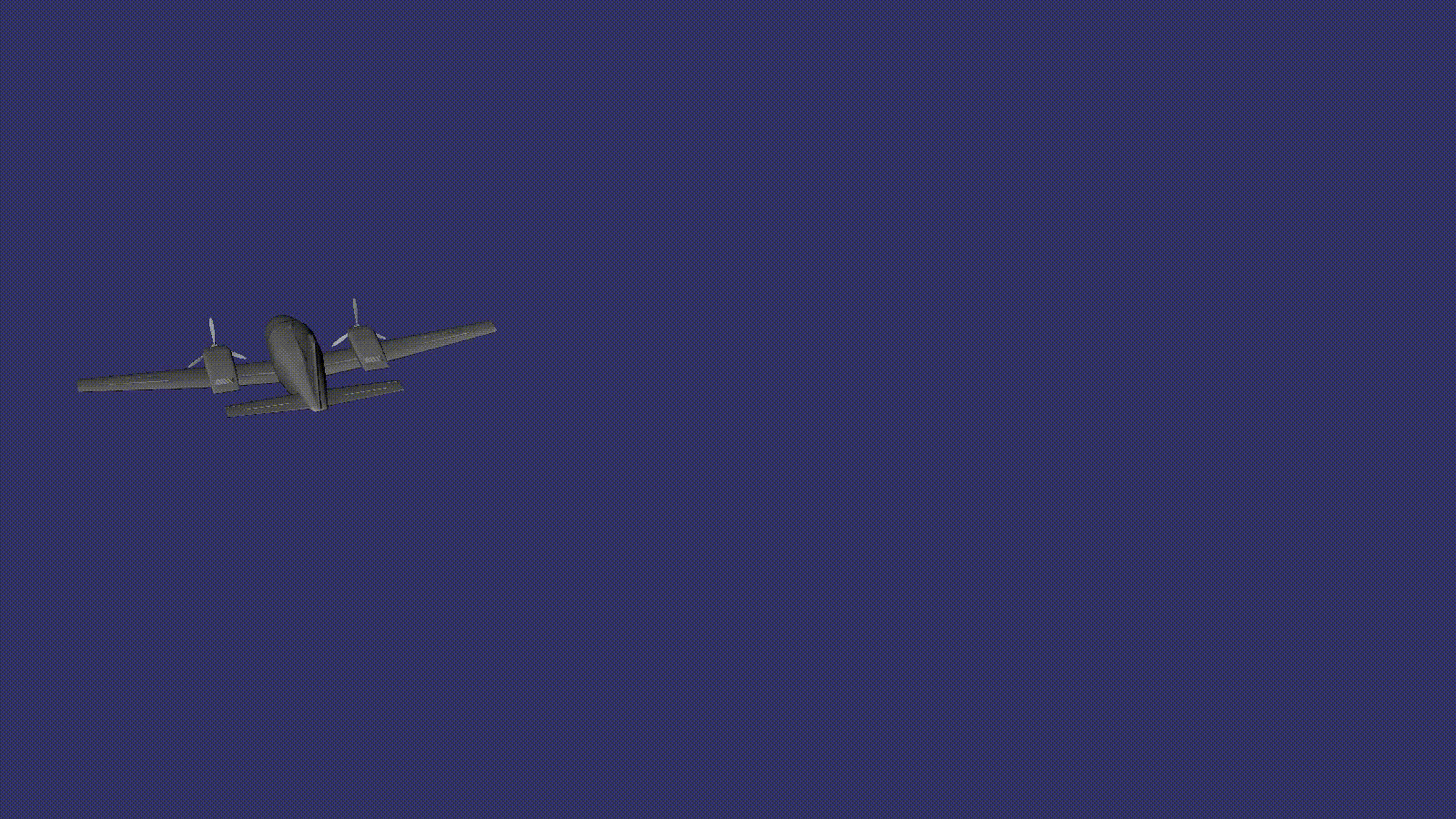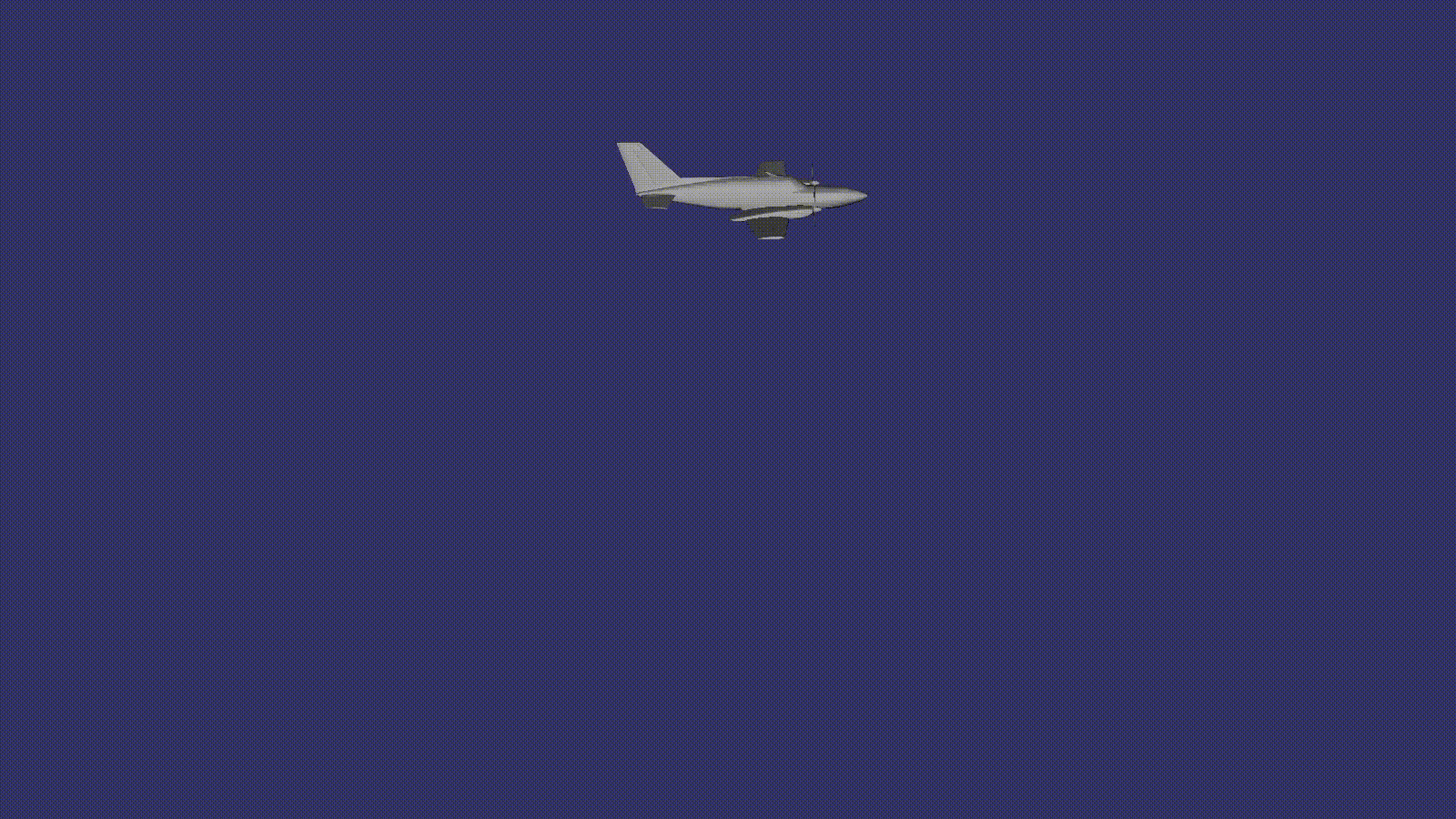
¿Crees que no encontraste nada extraño en este ejemplo? Anteriormente, por ejemplo, en un programa cuando se renderizaba a una textura, cambiaba explícitamente la matriz de transformación para lograr un cambio en la posición del modelo en el espacio. Aquí solo creamos un nodo de transformación y en el código no hay una asignación de matriz explícita en ningún lado.

El secreto es que la clase especial osg :: AnimationPathCallback hace este trabajo. De acuerdo con la posición actual del objeto en la ruta, calcula la matriz de transformación y la aplica automáticamente al nodo de transformación al que está conectado, salvando al desarrollador de un montón de operaciones de rutina.

Cabe señalar que adjuntar osg :: AnimationPathCallback a otros tipos de nodos no solo no tendrá ningún efecto, sino que también puede conducir a un comportamiento indefinido del programa. Es importante recordar que esta devolución de llamada solo afecta a los nodos de transformación.

5. Animación de control de software

La clase osg :: AnimationPathCallback proporciona métodos para controlar la animación durante la ejecución del programa.

1. reset (): reinicia la animación y reprodúcela primero.
   
2. setPause (): pausa la animación. Toma un valor booleano como parámetro
   
3. setTimeOffset (): establece el desplazamiento de tiempo antes del inicio de la animación.
   
4. setTimeMultiplier (): establece el factor de tiempo para la aceleración / desaceleración de la animación.
   

Por ejemplo, para eliminar la animación de la pausa y restablecer, ejecutamos dicho código

 apcb->setPause(false); apcb->reset(); 

y para comenzar la animación desde el cuarto segundo después de comenzar el programa con doble aceleración, tal código

 apcb->setTimeOffset(4.0f); apcb->setTimeMultiplier(2.0f); 

6. El orden de renderizar primitivas en OpenGL

OpenGL almacena vértices y datos primitivos en varios búferes, como un búfer de color, un búfer de profundidad, un búfer de plantilla, etc. Además, no sobrescribe los vértices y las caras triangulares ya enviadas a su tubería. Esto significa que OpenGL crea una nueva geometría, independientemente de cómo se creó la geometría existente. Esto significa que el orden en que se envían las primitivas a la canalización de representación afecta significativamente el resultado final que vemos en la pantalla.

Según los datos del búfer de profundidad, OpenGL dibujará correctamente objetos opacos, clasificando los píxeles de acuerdo con su distancia del observador. Sin embargo, al utilizar la técnica de mezcla de colores, por ejemplo, al implementar objetos transparentes y translúcidos, se realizará una operación especial para actualizar el búfer de color. Los píxeles nuevos y antiguos de la imagen se mezclan, teniendo en cuenta el valor del canal alfa (componente del cuarto color). Esto lleva al hecho de que el orden de renderizado de los bordes translúcidos y opacos afecta el resultado final



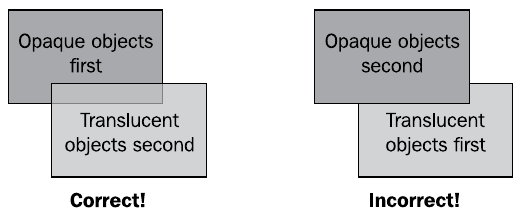
En la figura, en la situación de la izquierda, primero se enviaron objetos opacos y luego transparentes a la tubería, lo que condujo al cambio correcto en el búfer de color y a la visualización correcta de caras. En la situación correcta, primero se dibujaron objetos transparentes y luego opacos, lo que condujo a una visualización incorrecta.

El método setRenderingHint () de la clase osg :: StateSet indica a OSG el orden de representación requerido de nodos y objetos geométricos, si esto debe hacerse explícitamente. Este método simplemente indica si las caras translúcidas deben o no ser tomadas en cuenta al renderizar, asegurando así que si hay caras translúcidas en la escena, primero se dibujarán caras opacas y luego transparentes, teniendo en cuenta la distancia del observador. Para informar al motor que este nodo es opaco, usamos este código

 node->getOrCreateStateSet()->setRenderingHint(osg::StateSet::OPAQUE_BIN); 

o contiene bordes transparentes

 node->getOrCreateStateSet()->setRenderingHint(osg::StateSet::TRANSPARENT_BIN); 

7. Un ejemplo de la implementación de objetos translúcidos.

Tratemos de ilustrar toda la introducción teórica anterior con un ejemplo concreto de la implementación de un objeto translúcido.


En su mayor parte, el código que se muestra aquí no contiene nada nuevo: se crean dos objetos geométricos: un cuadrado texturizado y un ala delta, cuyo modelo se carga desde un archivo. Sin embargo, aplicamos un color blanco translúcido a todos los vértices del cuadrado.

 colors->push_back( osg::Vec4(1.0f, 1.0f, 1.0f, 0.5f) ); 

- el valor del canal alfa es 0.5, que, cuando se mezcla con colores de textura, debería dar el efecto de un objeto translúcido. Además, la función de mezcla de colores debe establecerse para el procesamiento de transparencia.

 osg::ref_ptr<osg::BlendFunc> blendFunc = new osg::BlendFunc; blendFunc->setFunction(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA); 

pasarlo a la máquina de estado OpenGL

 stateset->setAttributeAndModes(blendFunc); 

Al compilar y ejecutar este programa, obtenemos el siguiente resultado



Basta! ¿Y dónde está la transparencia? La cuestión es que olvidamos decirle al motor que se deben procesar los bordes transparentes, lo cual se resuelve fácilmente llamando

 stateset->setRenderingHint(osg::StateSet::TRANSPARENT_BIN); 

después de lo cual obtenemos el resultado que necesitamos: el ala del ala delta brilla a través de un cuadrado con textura translúcida



Los parámetros de las funciones de mezcla GL_SRC_ALPHA y GL_ONE_MINUS_SRC_ALPHA significan que el píxel de la pantalla resultante al dibujar una cara translúcida tendrá componentes de color calculados por la fórmula

 R = srcR * srcA + dstR * (1 - srcA) G = srcG * srcA + dstG * (1 - srcA) B = srcB * srcA + dstB * (1 - srcA) 

donde [srcR, srcG, srcB] son ​​los componentes de color de la textura cuadrada; [dstR, dstG, dstB] — , , . srcA - .

seRenderingHint() , , . , .

8.

. . , .

.

. , - , , 1 — . , 0 1 .


- -

 class AlphaFadingCallback : public osg::StateAttributeCallback { public: AlphaFadingCallback() { _motion = new osgAnimation::InOutCubicMotion(0.0f, 1.0f); } virtual void operator() (osg::StateAttribute* , osg::NodeVisitor*); protected: osg::ref_ptr<osgAnimation::InOutCubicMotion> _motion; }; 

_motion , . , ,

 AlphaFadingCallback() { _motion = new osgAnimation::InOutCubicMotion(0.0f, 1.0f); } 

InOutCubicMotion 0 1. operator()

 void AlphaFadingCallback::operator()(osg::StateAttribute *sa, osg::NodeVisitor *nv) { (void) nv; osg::Material *material = static_cast<osg::Material *>(sa); if (material) { _motion->update(0.0005f); float alpha = _motion->getValue(); material->setDiffuse(osg::Material::FRONT_AND_BACK, osg::Vec4(0.0f, 1.0f, 1.0f, alpha)); } } 

 osg::Material *material = static_cast<osg::Material *>(sa); 

callback , , , . — ,

 _motion->update(0.0005f); 

 float alpha = _motion->getValue(); 

 material->setDiffuse(osg::Material::FRONT_AND_BACK, osg::Vec4(0.0f, 1.0f, 1.0f, alpha)); 

main(). , — OSG

 osg::ref_ptr<osg::Drawable> quad = osg::createTexturedQuadGeometry( osg::Vec3(-0.5f, 0.0f, -0.5f), osg::Vec3(1.0f, 0.0f, 0.0f), osg::Vec3(0.0f, 0.0f, 1.0f)); 

, , . ,

 osg::ref_ptr<osg::Material> material = new osg::Material; material->setAmbient(osg::Material::FRONT_AND_BACK, osg::Vec4(0.0f, 0.0f, 0.0f, 1.0f)); material->setDiffuse(osg::Material::FRONT_AND_BACK, osg::Vec4(0.0f, 1.0f, 1.0f, 0.5f)); 

. Ambient color — , , . Diffuse color — , , , . FRONT_AND_BACK , , .

 material->setUpdateCallback(new AlphaFadingCallback); 

 geode->getOrCreateStateSet()->setAttributeAndModes(material.get()); 

— ,

 geode->getOrCreateStateSet()->setAttributeAndModes(new osg::BlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA)); geode->getOrCreateStateSet()->setRenderingHint(osg::StateSet::TRANSPARENT_BIN); 

 osg::ref_ptr<osg::Group> root = new osg::Group; root->addChild(geode.get()); root->addChild(osgDB::readNodeFile("../data/glider.osg")); osgViewer::Viewer viewer; viewer.setSceneData(root.get()); return viewer.run(); 

:

, . – main.h

 #include <osgAnimation/EaseMotion> 

OSG, , , , . osgAnimation/ , , ( )

 LIBS += -losgAnimation 

Continuará ...