Historia de Shipastik

Picos en todas partes

Lo llamamos Spikey, y en mi vida hoy lo encuentro constantemente:



Proviene de un objeto tridimensional, un poliedro llamado "sexagésimo rómbico".



Pero, ¿cuál es su historia y por qué lo convertimos en nuestro símbolo?

El origen de la espina

En 1987, cuando estábamos desarrollando la primera versión de Mathematica, una de sus innovaciones fue la posibilidad de generar gráficos tridimensionales independientes de la resolución basados ​​en descripciones simbólicas. En las primeras demostraciones, esto nos permitió producir imágenes sorprendentemente claras de poliedros regulares. Pero, al acercarnos al lanzamiento de Mathematica 1.0, queríamos usar un ejemplo más impresionante. Por lo tanto, decidimos tomar el último poliedro regular, el icosaedro , y hacer algo más complejo al darle una forma de estrella o, más correctamente, acumulación. Sí, así es como se veía la primera interfaz de portátil hace 30 años.



Al principio fue solo una buena demostración que funcionó bastante rápido en nuestras computadoras de esa época. Pero pronto el objeto tridimensional generado por él comenzó a ser utilizado de facto como un logotipo para Mathematica. Y para cuando se lanzó la versión 1.0 en 1988, el icosaedro estrellado estaba en todas partes:



Con el tiempo, comenzaron a aparecer varias dedicaciones a nuestro poliedro estelar, hechas en diferentes materiales y tamaños:



Pero, solo un año después del lanzamiento de Mathematica 1.0, estábamos listos para lanzar Mathematica 1.2, y para transmitir la complejidad del producto, necesitábamos un logotipo sofisticado. Uno de nuestros desarrolladores, Igor Rivin, defendió su tesis doctoral sobre poliedros en el espacio hiperbólico, y gracias a sus esfuerzos, los materiales para la versión 1.2 fueron decorados con un icosaedro hiperbólico:



Mis empleados me regalaron una camiseta con el Shipastik moderno para mi 30 cumpleaños en 1989, y una cita que apoyo incluso después de tantos años:


“La compañía es divertida”

Después del lanzamiento de Mathematica 1.2, en nuestros materiales de marketing se podía encontrar una colección completa de poliedros regulares hiperbólicos, pero con el advenimiento de la versión 2.0 en 1991, decidimos que nos gustaba más el icosaedro hiperbólico:



Pero continuamos explorando otras formas claveteadas. Inspirado por el dibujo de Leonardo da Vinci de un "modelo de madera" del icosaedro estrellado (hecho con una perspectiva sorprendentemente precisa) para el libro de Luke Pacioli "Sobre la proporción divina", pedimos un póster de la versión 2.0 donde cinco tetraedros de intersección están dispuestos de modo que sus vértices exteriores formen el dodecaedro:



Hoy, al revisar mis archivos de 1991, encuentro el código "explicativo", y es agradable ver que se ejecuta fácilmente en nuestra última versión de Wolfram Language (aunque hoy se puede escribir de manera un poco más elegante):



A lo largo de los años, esto se ha convertido en un extraño ritual: en preparación para el lanzamiento de la próxima versión principal de Mathematica, organizaremos reuniones serias en las que participaremos en "elegir un nuevo Shipastik". A veces tienes que elegir entre cientos de opciones diferentes creadas usando algoritmos completamente diferentes:



Pero, aunque las paletas de colores están mutando, y los Shipastiks a menudo reflejan la presencia de nuevas características en el sistema (aunque de manera algo implícita), tenemos una tradición de 30 años de elegir opciones para un dodecaedro hiperbólico:



Recientemente, se ha vuelto habitual estudiar el espacio paramétrico, aunque ahora ya hemos acumulado cientos de parámetros:



El dodecaedro hiperbólico tiene 20 picos: fue ideal para celebrar el 20 aniversario de Mathematica en 2008. Pero cuando queríamos hacer algo similar para el 25 aniversario en 2013, nos enfrentamos con el problema de la falta de poliedros regulares con 25 vértices. Pero (de hecho, utilizando la función SpherePoints [25]), pudimos crear una figura aproximada e imprimirla en una impresora 3D para todos los empleados de la empresa, con tamaños correspondientes a la duración del servicio de los empleados.

Salga de Wolfram | Alpha

En 2009, nos estábamos preparando para el lanzamiento de Wolfram | Alpha, y el sistema necesitaba un logotipo. Había muchos conceptos:



Queríamos enfatizar que Wolfram | Alpha funciona mediante cálculos, y no, por ejemplo, como un motor de búsqueda. Y durante algún tiempo quisimos usar algo con engranajes. Pero también queríamos que el logotipo se pareciera al logotipo de Mathematica de larga data. Esto dio lugar a uno de esos proyectos como "nuestro general se volvió loco": la creación de un mecanismo de engranajes a partir de formas claveteadas.

Un antiguo usuario de Mathematica y Wolfram Language, un ingeniero mecánico de Hungría, Sandor Kabai, nos ayudó proponiendo "engranajes con púas":



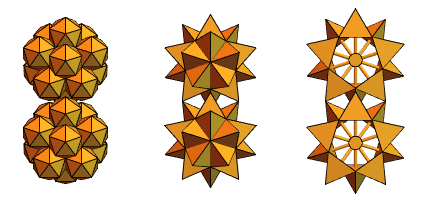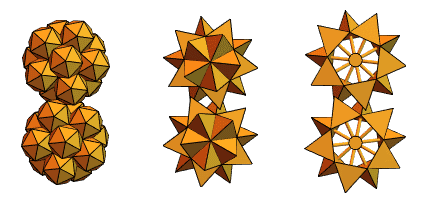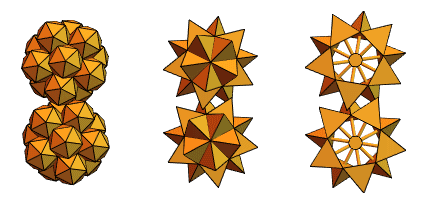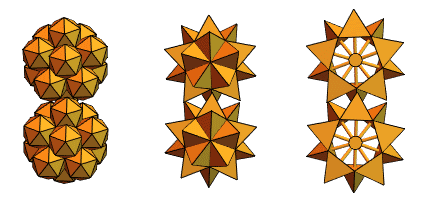
Volviendo a los tetraedros de intersección de la versión 2, creó algo como esto:



En 2009, las impresoras 3D se hicieron muy populares, y pensamos que sería bueno hacer un logotipo para Wolfram | Alpha que pudiera imprimirse. El poliedro hiperbólico no encajaba: los picos podían romperse y representar una amenaza. Las formas como picos de la cuarta versión, con "picos seguros", carecían de elegancia.

Por un tiempo nos aferramos a una idea con engranajes. Pero al final, decidieron que valía la pena echar un vistazo a los poliedros comunes. ¿Pero qué poliedro podemos elegir?

Por supuesto, hay un número infinito de poliedros posibles. Pero para nuestro logotipo, queríamos elegir un poliedro simétrico y, hasta cierto punto, "correcto". Cinco poliedros regulares (o "sólidos platónicos"), cuyas caras son los mismos polígonos regulares, pueden considerarse los "más regulares" de todos:



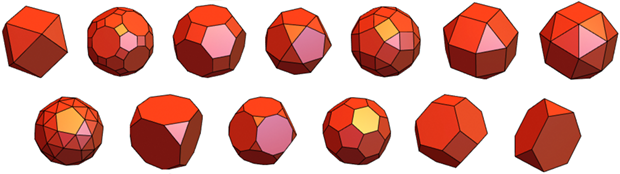
Hay 13 cuerpos Archimedean más: tienen vértices idénticos y los polígonos regulares, aunque de diferentes tipos, actúan como caras:



Hay muchos tipos de "corrección" de los poliedros. Un ejemplo es el "poliedro homogéneo" que muestra un póster de The Mathematica Journal de 1993:



Durante los años en que Eric Weinstein recopiló la colección, que en 1999 se había convertido en MathWorld, trató de incluir artículos sobre tantos polígonos como fuera posible. En 2006, como parte de la inclusión de varios datos sistematizados en Mathematica y Wolfram Language, comenzamos a incluir datos de polígonos con MathWorld. Como resultado, después del lanzamiento de la versión 6.0 en 2007, apareció la función PolyhedronData , que contenía datos completos sobre 187 polígonos notables:



En Mathematica y Wolfram Language, siempre puede generar polígonos regulares, pero ahora se ha vuelto más fácil de hacer. Con la versión 6.0, también lanzamos el Proyecto de Demostraciones Wolfram, que rápidamente comenzó a reponerse con varias demostraciones relacionadas con los poliedros.

Uno de ellos fue hecho por mi hija Katerina cuando tenía 10 años (hoy continúa desarrollándose en los campos de la geometría): estos son "koalas poliédricos", desglosados ​​por todos los poliedros de PolyhedronData [] utilizados:



En este contexto, en 2009 queríamos "elegir un poliedro" para Wolfram | Alpha. Todo se decidió el viernes 6 de febrero, cuando me puse a trabajar por mi cuenta.

He conservado ese cuaderno, y muestra que primero intenté implementar la dudosa idea de colocar esferas en los vértices de los poliedros:



Pero, como está registrado en el Historial del cuaderno , solo dos minutos después, cambié a poliedros puros, todos eran de color naranja, que luego queríamos usar para el logotipo:





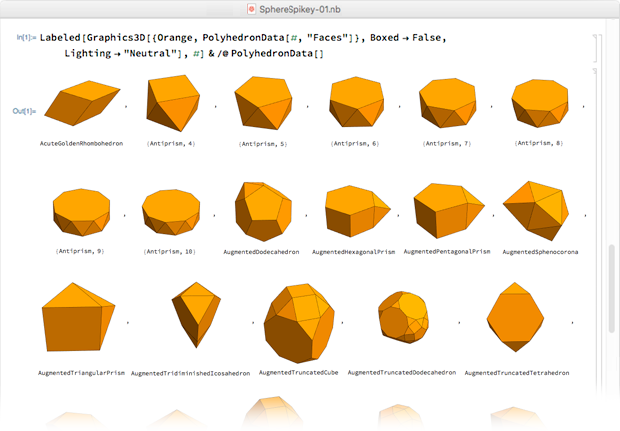
Los poliedros se organizaron en orden alfabético por nombre, y en la línea 28 apareció: un hexaedro rómbico.



Un par de minutos después, a las 00:24:24 del 7 de febrero de 2009, descubrí este hexaedro rómbico y lo convertí en una posición simétrica, que usamos ahora:



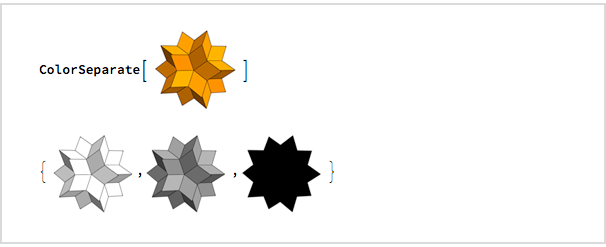
Quería ver cómo se vería en gris y en silueta, y cuatro minutos después usé ColorSeparate para descubrir:



Inmediatamente comencé a escribir un correo electrónico, que envié a las 00:32:

Realmente me gusta RhombicHexecontahedron. Tiene una forma interesante y muy simétrica. Me parece que su precisión nos queda bien, y la silueta se ve bastante razonable.



Obviamente, acabo de copiar RhombicHexecontahedron del cuaderno (dudo que pueda haber escrito el hexágono [hexecontahedron] sin errores). De mis archivos, sé que esta fue la primera vez que escribí el nombre del poliedro, que está destinado a convertirse en mi favorito.

En Wolfram Language, fue muy fácil obtener una imagen de un hexaedro rómbico y jugar con él:



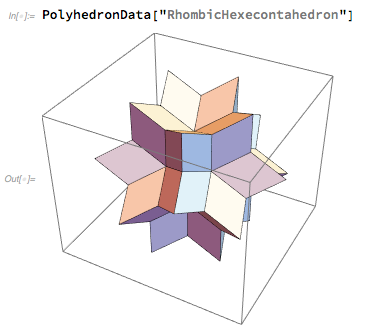
Para el lunes, estaba claro que el hexaedro rómbico había ganado, y nuestro departamento visual estaba ocupado dibujándolo como un logotipo para Wolfram | Alpha. Intentamos varias orientaciones, pero al final nos decidimos por la posición simétrica "a plena vista" que elegí. (También necesitábamos elegir la mejor "distancia focal" para el ángulo más adecuado).



Al igual que nuestro icosaedro estrellado de la versión 1.0, el hexaedro rómbico tiene 60 caras. Pero de alguna manera, gracias a las combinaciones de "cinco pétalos", se ve mucho más elegante. Se dedicó un gran esfuerzo a elegir tal sombreado de las caras para que el dibujo bidimensional reflejara correctamente el objeto tridimensional. Pero pronto presentamos la primera versión oficial de nuestro logotipo:



Rápidamente comenzó a aparecer en todas partes y, como tributo a nuestras primeras ideas, a menudo en un contexto decorado con engranajes:



Unos años más tarde, corregimos ligeramente el sombreado de los bordes, lo que condujo a la creación del logotipo Wolfram | Alpha, que todavía está en uso:



Hexágono rómbico

¿Qué es un hexaedro rómbico? En inglés, se llama hexecontahedron, porque tiene 60 caras, y ἑξηκοντα (hexeconta) es la palabra griega para "60". Sus caras son rombos dorados , que se llaman así porque sus diagonales están relacionadas entre sí de acuerdo con la proporción dorada: φ = (1 + √5) / 2 & sime; 1,618:



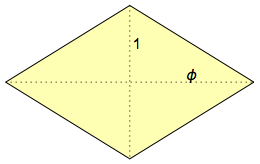
El hexaedro rómbico es un cuerpo intermedio interesante entre el icosaedro y el dodecaedro (con el icosododecaedro entre ellos). Los 12 vértices internos del hexaedro rómbico forman el icosaedro regular, y los 20 vértices externos forman el dodecaedro regular. 30 "picos intermedios" forman el icosododecaedro, 32 facetas (tiene 20 caras triangulares y 12 pentagonales):



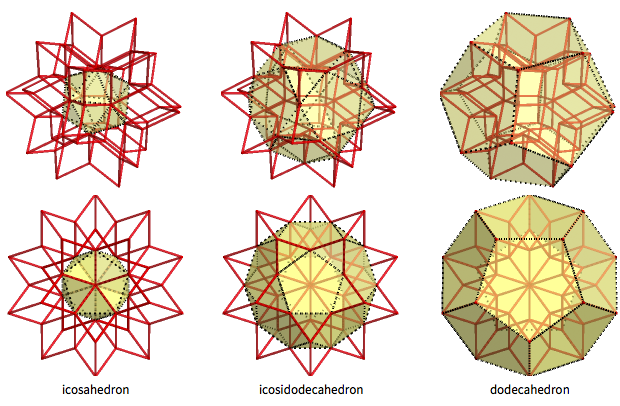
En total, el hexaedro rómbico tiene 62 vértices y 120 aristas (así como 120-62 + 2 = 60 caras). Tiene tres tipos de vértices ("interno", "medio" y "externo"), que corresponden a 12 + 30 + 20 vértices del icosaedro, icosododecaedro y dodecaedro. En estos vértices 3, 4 y 5 aristas convergen juntas, respectivamente. Cada cara tiene un vértice "interno" en el que se juntan 5 aristas, un vértice externo donde se juntan tres aristas y dos "intermedias" donde se juntan 4 aristas. Los vértices externo e interno son los vértices de ángulo agudo de los rombos dorados, y los intermedios son de ángulo obtuso.

El ángulo en los picos puntiagudos de los rombos dorados es 2 tan ⁻¹ (φ ⁻¹ ) ≈ 63.43 °, y en los picos romos es 2 tan ⁻¹ (φ) ≈ 116.57 °. Tales ángulos le permiten ensamblar un hexaedro rómbico del constructor Zometool usando solo los soportes rojos (como en el caso del dodecaedro):



De los 120 bordes del hexaedro rómbico de 60 "bisagras internas", el ángulo diédrico es 4π / 5 = 144 °, y para 60 externos es 2π / 5 = 72 °. Los ángulos contraídos por los vértices externo e interno son π / 5 y 3π / 5.

Para dibujar un hexaedro rómbico, debes conocer las coordenadas tridimensionales de sus vértices. Se obtienen convenientemente utilizando el hecho de que el hexaedro rómbico es invariante con respecto al grupo icosaedro, por lo que puede comenzar con un rombo dorado y simplemente agregar 60 matrices que forman una representación tridimensional del grupo icosaedro. Esto, por ejemplo, proporciona las coordenadas finales de los vértices en {± φ, ± 1,0}, {± 1, ± φ, ± (1 + φ)}, {± 2φ, 0,0}, {± φ, ± ( 1 + 2φ), 0}, {± (1 + φ), ± (1 + φ), ± (1 + φ)} y sus permutaciones cíclicas con todos los signos posibles.

Además del hecho de que las caras de un hexaedro rómbico son rombos dorados, se puede construir un hexaedro rómbico a partir de 20 romboedros dorados (en el que las seis caras son rombos dorados):



Hay otras formas de crear un hexaedro rómbico a partir de otros poliedros. Se puede obtener de cinco cubos de intersección y de 182 dodecaedros en contacto con caras:



No se puede diseñar un mosaico continuo de sesenta hexaedros rómbicos, pero se combinan bien entre sí (y, sí, vi docenas de Shipastiks de papel plegándose de esta manera):



También puede hacer todo tipo de anillos y otras configuraciones a partir de ellos:



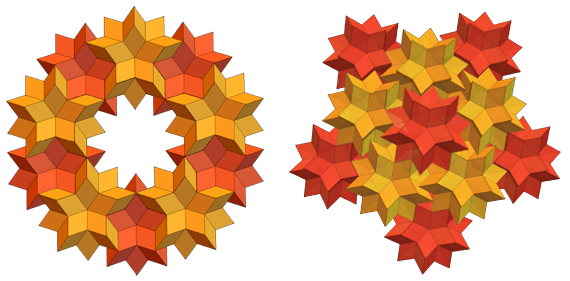
Un pariente cercano del hexaedro rómbico (RS) es el treinta-tetraedro rómbico (RT). RS y RT tienen caras que son rombos dorados. Pero RS tiene 60 de ellos, y RT tiene 30. Esto es lo que parece un RT separado:



Varios RT están perfectamente invertidos en los bolsillos de RS, y resultan cosas similares:



Sandor Kabay, mencionado anteriormente, se interesó en RSh y RT alrededor de 2002. Y después del lanzamiento del Proyecto de Demostraciones Wolfram, él, junto con el matemático esloveno Isidor Hafner, agregó más de cien demostraciones al proyecto relacionadas con RS, RT y muchas de sus propiedades:

Modelos de papel de punta

Tan pronto como decidimos que Shipastik sería un RS, comenzamos a hacer sus modelos 3D. Ahora es muy simple hacer esto usando la función Printout3D [PolyhedronData [...]], y los modelos ya calculados se pueden encontrar en recursos de terceros .

En mayo de 2009, cuando se lanzó Wolfram | Alpha, ya teníamos muchos Spikes 3D a mano:



Pero, preparándonos para la primera temporada de vacaciones después de este evento, decidimos darles a todos la oportunidad de hacer su propio Shipastik tridimensional. Primero, consideramos la opción con 20 imanes romboédricos recubiertos con plástico. Pero salieron caros y no se pegaron muy bien.

Esto nos llevó a la idea de hacer Shipastik de papel o cartón delgado. Por lo tanto, al principio queríamos hacer un esquema que se pudiera plegar en Shipastika:



Mi hija Katerina sirvió como probador (y todavía tiene una muestra de prueba), pero quedó claro que aparecen muchas situaciones incómodas en el proceso de plegado, en el que no está claro cómo moverse de una posición a otra. Puede hacer una gran cantidad de diseños (hay 43.380 de ellos solo para el dodecaedro y el icosaedro), y pensamos que tal vez sería posible elegir algo mejor de ellos:



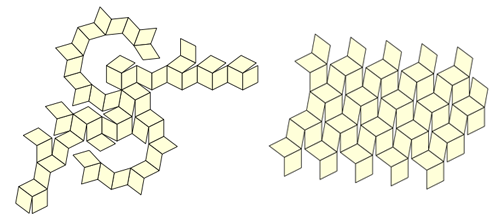
Pero, cuando no pudimos encontrar tal esquema, tuvimos una idea nueva (aunque obvia): si el modelo se aferraría a las orejas, ¿por qué no hacerlo con algunas piezas? Rápidamente nos dimos cuenta de que para esto solo necesitas tomar 12 piezas idénticas de este tipo:



Con su ayuda, creamos nuestros " sets para esculturas de papel ":



Una tarea interesante fue escribir instrucciones que fueran fáciles de entender, pero después de varias iteraciones, las instrucciones se volvieron bien desarrolladas y simples:



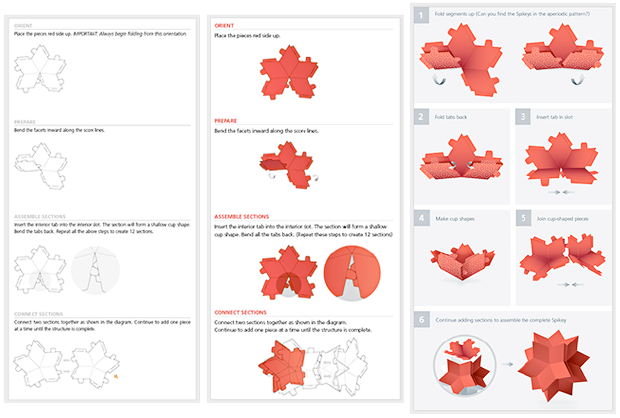
Y después del papel que Shipastiks envió a la gente, nuestros usuarios comenzaron a enviarnos todo tipo de imágenes de Shipastik "en el terreno":

El camino hacia el hexágono rómbico

El cubo de muchos lados del antiguo Egipto

No se sabe quién describió por primera vez los sólidos platónicos. Quizás esto fue hecho por los pitagóricos (que vivían cerca de depósitos tan grandes de cristales de pirita multifacéticos). Quizás alguien hizo esto mucho antes que ellos. Quizás fue contemporáneo de Platón, Teetet de Atenas . Pero, en cualquier caso, en la época de Platón (c. 400 a. C.), se conocían cinco sólidos platónicos. Y cuando Euclides escribió sus Elementos (c. 300 g a. C.), uno de los pilares de este trabajo fue la prueba de la ausencia de otros poliedros regulares. Esta prueba es conocida por dar el mayor número de pasos de los axiomas euclidianos originales: 32.

Se usaron sólidos platónicos para dados y adornos. Pero también se le asignó un papel central en el pensamiento sobre la naturaleza; por ejemplo, Platón sugirió que, en cierto sentido, todo podría consistir en ellos: tierra de cubos, aire de octaedros, agua de icosaedros, fuego de tetraedros y cielo ("éter" ) de dodecaedros.

¿Qué pasa con otros poliedros? En el siglo IV d.C. Papp de Alejandría escribió que un par de siglos antes de que Arquímedes descubriera otros 13 "poliedros regulares", aparentemente, lo que ahora se llama cuerpos de Arquímedes, aunque los detalles de esto se pierden. Y durante mil años, poco le ha sucedido a los poliedros. Pero en el siglo XV, con el comienzo del Renacimiento, los poliedros de repente se pusieron de moda nuevamente. Leonardo da Vinci y Albrecht Dürer los usaron regularmente en el arte y el diseño, redescubriendo algunos de los cuerpos de Archimedean, así como descubriendo nuevos poliedros, por ejemplo, el icodosodecaedro.

Pero el mayor paso adelante para los poliedros fue el trabajo de Johannes Kepler a principios del siglo XVII. Todo comenzó con una teoría elegante, aunque completamente incorrecta. Kepler, sobre la base de suposiciones teológicas, creía que el Universo debería crearse con precisión matemática, y sugirió que los seis planetas conocidos en ese momento se mueven a lo largo de esferas anidadas inscritas y descritas alrededor de cinco sólidos platónicos:



En su libro de 1619 Harmonices mundi, Harmony of the World, Kepler argumentó que muchas características de la música, los planetas y las almas funcionan de acuerdo con relaciones y principios geométricos similares. Para confirmar los argumentos, Kepler estudió polígonos y poliedros, especialmente interesándose en los objetos que forman conjuntos completos, como los sólidos platónicos.

Estudió los "poliedros de contacto" con los que pavimentar el avión, y encontró, por ejemplo, " mosaicos monstruosos ", como los llamó (que consisten en pentágonos, pentagramas y decágonos). Estudió los "poliedros estrellados" y encontró varias versiones estrelladas de sólidos platónicos (y Kepler - cuerpo de Poinsot ). En 1611, publicó un pequeño libro sobre la estructura hexagonal de los copos de nieve, escrito como un regalo para el año nuevo a uno de sus patrocinadores. En este libro, discutió el empaque tridimensional de esferas (y átomos esféricos), proponiendo la hipótesis de que el empaque más denso de bolas en el espacio tridimensional (observamos regularmente su implementación en paquetes de frutas en las tiendas) es un empaque cúbico centrado en la cara (esta hipótesis se demostró formalmente solo después de 2000 años - usando Mathematica).

En varios paquetes de Kepler, se ocultan diferentes poliedros. Comencemos desde cualquier esfera, tomemos sus vecinos y conectemos sus centros para formar los vértices del poliedro. En el empaque más apretado de Kepler, otros 12 tocan cualquier esfera, y de sus centros se obtiene un cuboctaedro con 12 vértices y 14 caras. Pero Kepler también describió otro paquete, un 8% menos denso, en el que cada esfera está cubierta por otras 8, y otras 6 están muy cerca. Si conectamos sus centros, obtenemos un dodecaedro rómbico, con 14 vértices y 12 caras:



Después de descubrir esto, Kepler comenzó a buscar otros "poliedros rómbicos". En el dodecaedro rómbico que encontró, los rombos consistían en pares de triángulos equiláteros. Pero en 1619, Kepler también estudió rombos dorados, y encontró un rombo de treinta lados, después de lo cual pintó en su libro su hermosa imagen, al lado del dodecaedro rómbico:



Kepler inmediatamente encontró aplicación para polígonos rómbicos: quería usarlos y un cubo para construir un modelo de esferas anidadas adecuadas para las órbitas de las cuatro lunas de Júpiter descubiertas por Galileo en 1610.

¿Por qué Kepler no abrió el hexaedro rómbico? Creo que se acercó bastante a él. Estudió poliedros estrellados no convexos. Miró los poliedros rómbicos. Pero, aparentemente, para sus teorías astronómicas, un rombo de treinta lados fue suficiente, después de lo cual dejó de buscar.

Como resultado, por supuesto, las leyes de Kepler, no relacionadas con el poliedro, se convirtieron en la principal contribución a la astronomía que sobrevivió. Pero el trabajo de Kepler sobre el poliedro, aunque llevado a cabo en el marco de una teoría física incorrecta, sigue siendo una contribución eterna a las matemáticas.

Durante los siguientes tres siglos, se encontraron más poliedros de varias correcciones, y para principios de XX los matemáticos ya conocían muchos de sus tipos:



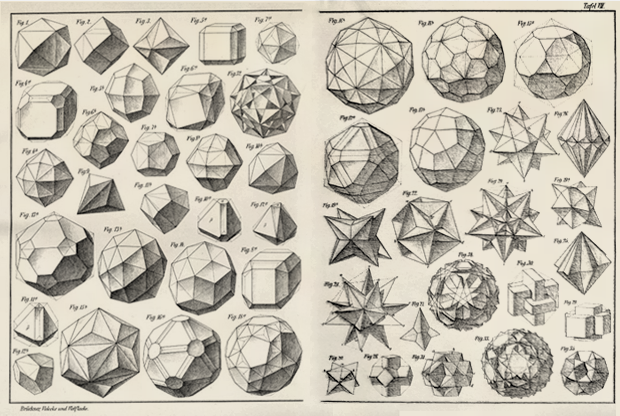
Pero, por lo que puedo decir, no había RS entre ellos. Su descubrimiento aguardaba el trabajo de Helmut Unkelbach . Nacido en 1910, defendió su doctorado en matemáticas en la Universidad de Munich en 1937 (aunque primero estudió física). Escribió varios trabajos sobre mapeo conforme y, tal vez debido al estudio del mapeo de poliedros, en 1940 publicó el trabajo "Poliedros simétricos de borde" en alemán.

Explicó que su objetivo era un estudio exhaustivo de todos los poliedros posibles que satisfagan una nueva definición especial de corrección: todos los bordes tienen la misma longitud y están en el plano de simetría del poliedro. El resultado principal del trabajo fue una tabla con 20 poliedros diferentes de esta propiedad:


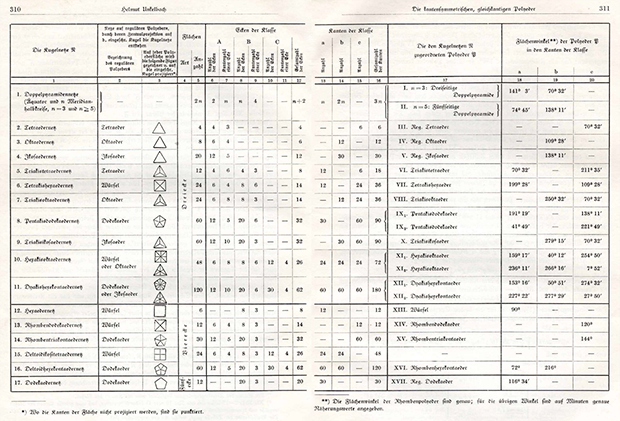Clickable

La mayoría de ellos ya eran famosos. Pero Unkelbach destacó tres de ellos que consideraba nuevos: dos hexaciscosahedra (o disdakis dodecahedron), dos hexacisicosahedra (o disdacystriacontahedron) y lo que llamó Rhombenhexekontaeder, o un hexahedron rómbico. Y él claramente consideró a RSh su principal logro, e incluyó una fotografía de su modelo hecha por él mismo:



¿Cómo trajo RS? Comenzó con el dodecaedro y definió dos de su plano de simetría:



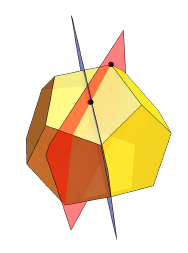
Luego dividió cada una de sus caras:



Luego, en esencia, exprimió los centros de cada una de las caras en una distancia igual a la distancia habitual al centro multiplicada por un cierto α:



Para α <1, las caras resultantes no se cruzan. Pero para la mayoría de los valores de α, sus lados no eran iguales. Esto sucede solo en un caso determinado, cuando el poliedro resultante coincide exactamente con el RS.

Unkelbach consideró su trabajo de 1940 como un "calentamiento" para un estudio más extenso de "poliedros simétricos k" con requisitos de simetría menos estrictos. Pero ya, por supuesto, fue un milagro que después del comienzo de la Segunda Guerra Mundial , se publicó una revista matemática en Alemania; poco después de esta publicación, Unkelbach fue llamado al frente, donde desarrolló torpedos acústicos para la flota alemana durante varios años.

No publicó más trabajos sobre poliedros, y murió en 1968. Después de años, volvió al mapeo conforme, y también comenzó a publicar sobre la teoría de la votación , considerándola la clave para crear una democracia que funcione bien, y pensando que los matemáticos estaban obligados a hacer que la gente comenzó a usarlo.

Pero, incluso apareciendo en un trabajo de 1940, el RS podría quedarse allí para siempre si en 1946 alguien Harold Scott MacDonald Coxeter no escribió una breve reseña de este trabajo para la revista relativamente nueva American Mathematical Reviews. Su revisión enumera los poliedros mencionados en el trabajo, ya que un naturalista puede enumerar nuevas especies descubiertas por él en una expedición. Lo principal es que describió allí el "hexaedro rómbico notable", y mencionó que "la forma de sus caras coincide con la forma de las caras de los treinta lados, de la cual se obtiene dando una forma de estrella".

Los poliedros no eran un tema popular en matemáticas a mediados del siglo XX, pero Coxeter era su principal defensor, y de alguna manera estaba conectado con todos los que los estudiaron. En 1948, publicó el libro The Right Political Scientists. Describe sistemáticamente varias familias de poliedros regulares, en particular, y el gran poliedro estrellado de treinta lados; de hecho, contiene un RS:



Pero en su libro, Coxeter no menciona explícitamente a RS, y aunque fue honrado con las referencias de algunos amantes de los poliedros, RS siguió siendo poco conocido.

Cuasicristales

Los cristales siempre han sido ejemplos importantes de poliedros en la naturaleza. Pero en el siglo XIX, cuando la teoría atómica estaba ganando cada vez más reconocimiento, los científicos comenzaron a realizar investigaciones cada vez más serias en el campo de la cristalografía y la disposición de los átomos en los cristales. Los poliedros comenzaron a aparecer con frecuencia, en particular, en representaciones de la geometría de bloques repetitivos de átomos ("células") en cristales.

En 1850, se sabía que solo puede haber 14 geometrías de este tipo, entre ellas también hay una basada en el dodecaedro rómbico. Son notables por la presencia de simetrías de segundo, tercer, cuarto o sexto orden, que, en esencia, es una consecuencia del hecho de que el espacio solo puede llenarse con ciertos poliedros, al igual que solo los polígonos regulares como los cuadrados pueden llenar un plano bidimensional, triángulos y hexágonos.

¿Qué pasa con otros materiales no cristalinos, como líquidos o vidrio? Desde principios del siglo XX, la gente ha estado interesada en la posibilidad de la presencia de al menos simetrías aproximadas de quinto orden allí. No será posible llenar el espacio con los icosaedros correctos, pero es posible crear secciones de espacio de veinte lados con pequeños espacios entre ellos.

Esta pregunta permaneció sin resolver hasta la década de 1980, cuando la cristalografía de difracción de electrones usando una aleación de aluminio y manganeso enfriada rápidamente demostró la presencia de una simetría quíntuple. Las teorías para lograr esta simetría ya existían, y después de unos años, también aparecieron imágenes hechas por un microscopio electrónico, en las cuales las partículas que tenían la forma de un rombo de treinta lados eran visibles:



Y mientras la gente imaginaba cómo estos treinta heptaedros se pueden combinar entre sí, un hexaedro rómbico apareció como un "agujero" en un grupo de 12 trihedros rómbicos:



Al principio se llamaba una estrella de 20 puntas. Pero luego se asoció con descripciones en la literatura sobre el poliedro, y se identificó como RS.

Mientras tanto, la idea de crear objetos a partir de elementos rómbicos estaba ganando cada vez más popularidad. Michael Longe Higgins, oceanógrafo y experto en formación de olas oceánicas, se unió al pasatiempo masivo, y en 1987 patentó un juguete basado en elementos romboédricos, desde el cual era posible ensamblar una "estrella de Kepler" (RS) o una "bola de Kepler" (rombo treinta ):



Y, aunque solo lo descubrí ahora, los bloques romboédricos, que consideramos en 2009 como una opción para crear "Shipastiks", en realidad fueron producidos por la compañía Dextro Mathematical Toys (Rhombo.com), que trabajó en la base de Longge-Higgins en San Diego

La cuestión de llenar con éxito el espacio con figuras tridimensionales, o incluso un plano con figuras bidimensionales, es bastante complicada. Se sabe desde la década de 1960 que, en el caso general, el problema de si un determinado conjunto de formas puede llenar un plano no tiene solución. (En principio, se puede verificar si 1000 de estos formularios se pueden componer entre sí, pero cuantos más formularios consideremos, más recursos informáticos requerirá).

Las personas como Kepler probablemente asumieron que si un conjunto de formas pudiera llenar un plano, entonces esto podría hacerse como un patrón repetitivo. Sin embargo, después de que quedó claro que, en el caso general, este problema no se resolvió, Roger Penrose en 1974 ideó dos formas que pueden llenar el plano sin repetir patrones. Para 1976, Penrose (y Robert Ammann) habían presentado una versión simplificada de estas formas:



Y sí, estas formas parecen rombos, aunque no oro. Pero con ángulos de 36 °, 144 ° y 72 °, 108 °, tienen una simetría de 5 y 10 veces.

Estos rombos no pueden diseñar patrones repetitivos. Pero resulta que pueden diseñar un patrón construido de forma sistemática anidada:



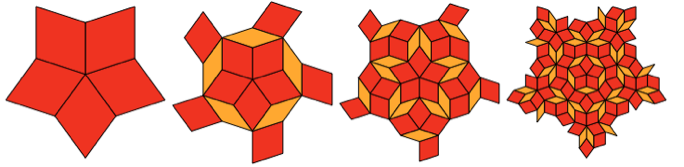
Y sí, la parte media del tercer paso es muy similar al Shipastik aplanado. Pero no coincide completamente con él, los rombos externos tienen un formato ligeramente diferente.

Sin embargo, todavía existe una estrecha conexión entre ellos. Imagine que comenzaremos no desde un avión, sino desde la mitad de un rombo tridimensional de treinta cuadrados, que consiste en rombos dorados:



Desde arriba, se ve exactamente como el comienzo del diseño de mosaico de Penrose anidado. Si continuamos este proceso, obtenemos este mosaico:



Si lo miras "desde un lado", puedes ver que estos siguen siendo los mismos rombos dorados:



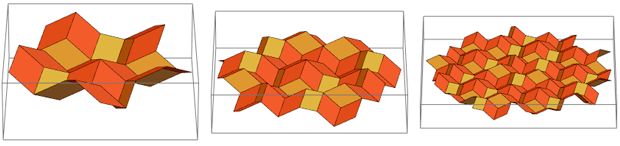
Después de haber compilado cuatro de estos "techos Wieringa", puede obtener solo RS:



¿Cuál es la relación entre estas estructuras incrustadas y la forma real de formar cuasicristales físicos? Aún no está claro. Pero es bastante interesante ver cómo aparecen indicios de RS en la naturaleza.

Históricamente, fue gracias a la discusión de cuasicristales que Sandor Kabaei comenzó a estudiar RS utilizando Mathematica, lo que llevó a Eric Weinstein a descubrirlos, lo que llevó a su inclusión en Mathematica y Wolfram Language, lo que me llevó a elegir uno de ellos para nuestro logotipo. En honor a esto, imprimimos un mosaico de Penrose dentro de nuestro Paper Shipastik:

Espina aplastante

Nuestro Shipastik para Wolfram | Alpha irrumpió en el mundo en 2009 con el lanzamiento de Wolfram | Alpha. Pero también tenemos nuestro Shipastik para Mathematica, que se ha desarrollado y evolucionado durante mucho tiempo. Por lo tanto, cuando construimos nuestra nueva sede europea en 2011, dos Shipastiks compitieron por la presencia en ella.

A nuestro antiguo director de arte Jeremy Davis se le ocurrió lo siguiente: tomar uno de los Shipastiks e "idealizarlo" usando solo su "esqueleto". La decisión de comenzar con RS fue simple. Pero luego lo aplastamos, por lo que apareció la primera versión del logotipo ahora familiar:

Sorpresa brasileña

Cuando comencé este artículo, pensé que toda la historia terminaría allí. Después de todo, ya he descrito cómo elegimos RS para nosotros, y cómo se les ocurrió a los matemáticos. Pero antes de terminar de escribir, decidí: "Revisaré todas las cartas sobre Shipastik durante todos los años, solo para asegurarme de que no me he perdido nada".

Y luego noté un correo electrónico de junio de 2009 de la artista brasileña Yolanda Kipriano. Ella escribió que vio un artículo sobre Wolfram | Alpha en una revista de noticias brasileña, llamó la atención sobre Shipastika y proporcionó un enlace a su sitio. Han pasado más de 9 años desde entonces, pero aún seguí este enlace y me sorprendió ver lo siguiente:



Continué leyendo su carta: "En Brasil, este objeto se llama Giramundos o la" flor de Mandakaru "y está hecho de servilletas como adorno artístico".

Que? En Brasil hay una tradición asociada con Shipastik, y durante todos los años no hemos oído hablar de ella. Pronto descubrí sus imágenes en la red. Una pequeña parte de los modelos estaba hecha de papel, la mayoría estaba hecha de tela, pero había muchos de ellos:



Le escribí a mi amigo brasileño que trabajó en las primeras versiones de Wolfram | Alpha. Él rápidamente respondió: “Estos objetos realmente parecen familiares. Para mi vergüenza, no tenía el deseo suficiente de comparar dos y dos ", y me envió fotos del catálogo local de obras de arte y artesanías:



La caza comenzó: ¿qué eran estos objetos y de dónde provenían? Alguien de nuestra compañía dijo que su bisabuela de Chile tejió esas cosas y siempre las hizo cola. Comenzamos a ponernos en contacto con personas que publicaron fotos de "shipastiks populares" en la red. Muy a menudo resultó que compraron sus copias en las tiendas. Pero a veces las personas decían que sabían cómo hacerlas. Y todos tenían casi la misma historia: aprendieron esto de sus abuelas.

Una forma típica de recolectar espigas populares, al menos en nuestro tiempo, es cortar 60 diamantes de cartón. Luego, todos deben envolverse en tela y coserlos juntos:



Pero entonces surge un problema matemático de inmediato. ¿Están estas personas marcando y tallando correctamente rombos dorados con un ángulo de 63 °? Por lo general no. Hacen rombos con 60 ° a partir de pares de triángulos equiláteros: esta es la forma romboidal estándar utilizada en la fabricación de colchas. Entonces, ¿cómo surgen los Thornies? Bueno, la diferencia entre 60 ° y 63 ° es pequeña, y si cose las caras juntas, entonces habrá suficiente espacio entre ellas para maniobrar, por lo que es bastante simple hacer un poliedro sin lograr ángulos absolutamente precisos. (También hay cuasi-Shipastiks, en los que, como en la construcción de Unkelbach, en lugar de caras no hay rombos, sino "triángulos externos" afilados).

Los picos en Internet se designan de manera diferente. Muy a menudo - Giramundos. A menudo se les llama Estrelas da Felicidade ("estrellas de la felicidad"). El hecho de que a veces se les llame "estrellas de Moravia" es confuso, pero de hecho, las estrellas de Moravia son poliedros mucho más afilados (a menudo hechos de rombocubooctaedro), que recientemente han ganado popularidad como luminarias.

A pesar de una larga investigación, todavía no conozco toda la historia de los picos populares. Aquí está lo que descubrí.En primer lugar, la mayoría de los picos populares de hoy se concentran en Brasil (aunque tenemos historias sobre su aparición en otros lugares). En segundo lugar, la tradición parece bastante antigua, definitivamente apareció mucho antes del siglo XX y, quizás, varios siglos antes. Por lo que puedo decir, se pasa de boca en boca, como suele ser el caso del arte popular, y no he encontrado ningún documento histórico real sobre este tema.

La mejor información me la proporcionó alguien Paula Guerra, que vendía picos populares en un café turístico que ella administraba hace diez años, ubicado en la histórica ciudad de São Luis do Paraiting. Ella dijo que personas de todo Brasil vinieron a su café, vieron picos populares, y dijeron algo como "No he visto esas cosas en 50 años".

Paula misma aprendió sobre los picos populares (los llama "estrellas") de una mujer mayor que vivía en una granja familiar, que los había estado haciendo desde que era una niña, y aprendió esto de su madre. Su proceso, aparentemente típico, consistió en juntar cartón en algún lugar (originalmente era algo así como cajas de sombreros), cubrir las piezas con tela y unirlas para obtener un objeto de unos 15 cm de tamaño.

¿Cuántos años tiene un hombre de punta? Esto solo puede ser apreciado por la tradición oral. Encontramos varias personas que vieron cómo los parientes nacían en el área de 1900 de shipastiks. Paula dijo que hace diez años se reunió con una mujer de 80 años que le dijo que cuando crecía en una granja de café hace 200 años, había un estante completo donde había picos populares hechos por cuatro generaciones de mujeres.

Parte de la historia del shipastik nacional parece girar en torno a las tradiciones transmitidas de madre a hija. Se dice que las madres a menudo hicieron espigas como regalos de boda para sus hijas. Por lo general, los shipastiks se hicieron con restos de ropa y otras cosas que recuerdan a las hijas sobre su infancia, algo así como las colchas de retazos que hoy hacen los niños que van a la universidad.

Sin embargo, se descubrió otro giro con los picos populares: a menudo, antes de coser un juguete, la madre ponía dinero que su hija podía usar en casos críticos. Y la hija mantuvo su shipastik junto con sus suministros de costura, donde su esposo difícilmente lo habría encontrado. Algunas espigas se usaron como alfileres de almohadas, lo que puede haber servido como un obstáculo adicional para los esposos.

¿Qué familias apoyaron la tradición de hacer espigas populares? Desde aproximadamente 1750, ha habido muchas plantaciones de café y azúcar en las zonas rurales de Brasil, alejadas de las ciudades. Hasta aproximadamente el siglo XX, los agricultores a menudo llevaban a las niñas a sus novias, a menudo muy jóvenes, de hasta 13 años, de ciudades remotas. Quizás estas novias, generalmente provenientes de buenas familias de ascendencia portuguesa, con una educación relativamente buena, llevaban espinas populares.

Aparentemente, con el tiempo, la tradición se extendió a las peores familias, y básicamente permaneció allí. Pero en algún lugar a mediados del siglo XX, probablemente cuando comenzaron a aparecer caminos en el país, comenzó la urbanización y la gente comenzó a abandonar las granjas, la tradición casi se extinguió. Sin embargo, en las escuelas rurales del sur de Brasil en la década de 1950, a las niñas se les enseñaba en clases de arte para hacer pinchos populares con una ranura especial para usar como huchas.

Los picos populares tienen una historia diferente en diferentes partes de Brasil. En las regiones fronterizas del sur (cerca de Argentina y Uruguay) existe una tradición según la cual "la estrella de San Miguel "(ella también es una shipastik popular) fue hecha en las aldeas por mujeres sanadoras (es decir," brujas ") que, durante la fabricación de juguetes, tenían que pensar en la salud del paciente.

En otras partes de Brasil, los juguetes a menudo se llamaban nombres de flores y frutas que se parecían un poco a ella. En el noreste - Flor Mandacarú (por el nombre de las flores de cactus). En humedales tropicales - Carambola (después de las frutas de carambola, a veces llamadas "estrellas tropicales"). En las regiones boscosas centrales - Pindaíva (en honor a la fruta de punta roja).



Pero la mayoría de las veces, la popular shipastika se llama Giramundo, una palabra portuguesa bastante antigua que literalmente significa "mundo arremolinado". Aparentemente, los juguetes fueron utilizados como amuletos que traen buena suerte con su rotación en el viento. Las colas comenzaron a unirse a ellas recientemente, pero, aparentemente, era costumbre colgarlas en casas, posiblemente en días festivos.

A menudo no está claro cuál de las tradiciones que dieron origen a la shipastika era original y cuál apareció recientemente. En el desfile en honor del festival de la Epifanía (el nombre local es "el día de los tres reyes") en São Luis do Paraiting, se usaron clavos populares como símbolo de la Estrella de Belén, pero esto, aparentemente, no es una tradición muy antigua, y claramente no muestra ninguna conexión. con religión

Encontramos varios ejemplos de picos populares que aparecen en exposiciones de arte. Una de ellas, realizada en 1963 y dedicada al arte popular del noreste de Brasil, fue organizada por la arquitecta Liina bo Bardi. El otro, donde se exhibió el más grande de los picos tridimensionales que he visto, fue organizado en 1997 por el arquitecto y diseñador Vladavio Imperio:



Entonces, ¿de dónde vienen las espigas populares? Todavía no lo sé. Podrían aparecer en Brasil, podrían venir de Portugal u otra parte de Europa. El hecho de que usaran piezas de tela y costura para su fabricación puede ser un argumento a favor de su origen africano o nativo americano.

Una artesana moderna que hace shipastiks dijo que su bisabuela, que hizo tales juguetes y nació a fines del siglo XIX, proviene de una región de Italia llamada Romagna (y una dijo que aprendió a hacer shipastiks con su abuela, que provenía de canadienses franceses). Creo que es muy posible que los picos populares fueran comunes en Europa, pero se extinguieron hace muchas generaciones, y esta tradición no sobrevivió allí. Y aunque en las pinturas europeas de siglos anteriores aparecen muchos poliedros diferentes, no conozco ninguna imagen de Shipastik entre ellos (tampoco he visto Shipastik en el arte islámico).

Pero estoy bastante seguro de que las espigas populares tienen un punto de origen. Tal cosa difícilmente se habría inventado dos veces.

Debo decir que esta no es mi primera cacería en el campo del arte. La búsqueda del primer patrón incrustado ( Sierpinski ) resultó ser más exitosa , lo que finalmente me llevó a la cripta en la iglesia italiana, donde vi cómo este patrón se descubrió gradualmente utilizando un ejemplo de un mosaico de piedra que data del siglo XIII.

Hasta ahora, Shipastik no se ha rendido tan fácilmente, y complica la situación es el hecho de que básicamente estaba hecho de tela que no sigue siendo tan buena como la piedra.

Los picos cobran vida

Cualquiera sea su origen, Shipastik desempeña el papel de un logotipo fuerte y digno. Pero a veces es divertido revivir el Shipastik, y a lo largo de los años hemos producido varios Shipastiks personalizados por varias razones:



al usar Wolfram | Alpha, el sistema generalmente muestra un Shipastik geométrico. Pero a veces su solicitud lo anima, por ejemplo, solicitudes de π el día pi:

blog.stephenwolfram.com/data/uploads/2018/12/spikey-lives-happy-pi-day-video.mp4

Picos para siempre

Los poliedros son eternos. Se pueden ver en la imagen de hace 500 años, que se ve tan clara y moderna como el poliedro en mi computadora.

Pasé mucho tiempo buscando cosas informáticas abstractas (por ejemplo, autómatas celulares). También tienen algo de atemporalidad. Pero para ellos no encontré ninguna evidencia histórica. Al igual que los objetos abstractos, podrían crearse en cualquier momento. Pero aparecieron hoy gracias a nuestras plataformas y herramientas conceptuales, y nadie las ha visto antes.

La rica historia y la constancia de los poliedros tienen miles de años. En apariencia, se parecen a las gemas. Encontrar el poliedro correcto de cierto tipo es como encontrar una gema en un universo geométrico de todas las formas posibles.



RS es una de esas piedras increíbles y, al estudiar sus propiedades, comencé a apreciarla aún más. Pero también es una joya con una historia humana, y es terriblemente interesante ver cómo tal abstracción, como un poliedro, puede unir a personas de todo el mundo con una historia y objetivos tan diferentes.

¿Quién fue el primero en inventar el hexaedro rómbico? No lo sabemos, y puede que nunca lo sepamos. Pero ahora que lo tenemos, él se quedará con nosotros para siempre. Mi poliedro favorito