Civilización de primavera, 1/5

### Parte 1. Golden "Ku"

Aproximadamente seis años caí en manos de un guía de abuelo ^[50] en camiones de mediados del siglo XX. Sólido, impreso en papel grueso liso libro raro. Lo único que queda en la memoria de mi abuelo después del colapso del país, las guerras y los viajes.



El libro de referencia contenía muchas características de rendimiento interesantes, por lo que la palabra "capacidad de carga" me resultó familiar desde la primera infancia. Y cuando mi padre en una caminata mencionó que cualquier camión pesa tanto como se necesita, lo recuerdo. Recordó y, mucho después, se interesó.

Papá tenía razón. Para los camiones de los años 60, esta regla se implementa con una precisión bastante sorprendente:



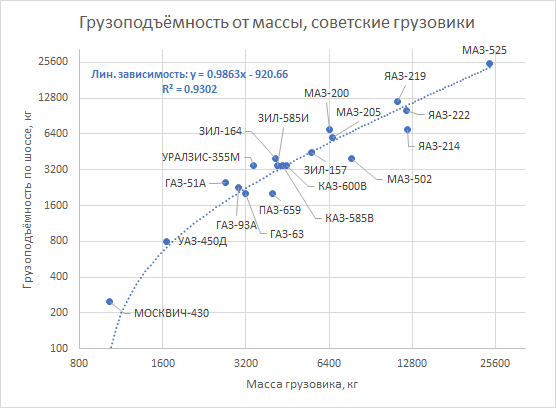
Es mucho más curioso que este patrón también se observe en vehículos que son completamente diferentes a los camiones.

Al principio, por diversión, puse aviones de carga en el horario. Y se sorprendió. Comencé a agregar otros vehículos. Montar, flotar y volar, construido en los siglos XIX, XX y XXI, trabajando en la energía térmica, atómica, eólica e incluso a caballo. Resultado? Potencia débil (indicador 1.125), si no solo lineal, dependencia. En masas de cientos de kilogramos a sesenta mil toneladas. Con desviaciones, por supuesto, a dónde podría ir sin ellas, hasta 10 veces a veces, pero en seis órdenes de masa esto es obviamente trivial.

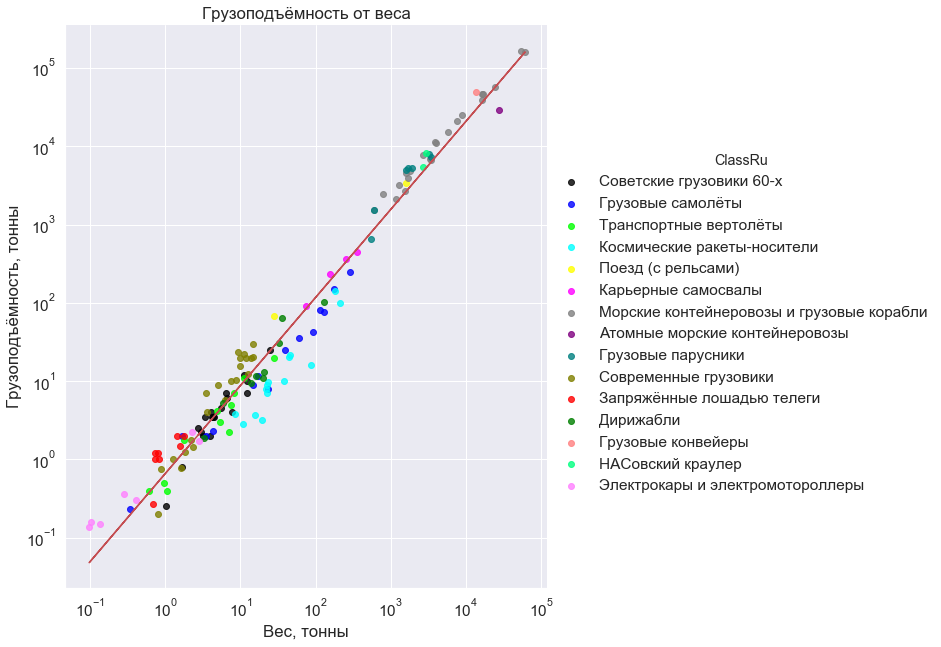
Aquí está, esta dependencia, apretando a la diagonal de un vasto campo vacío:


En el cuadro anotado: avión de carga; helicópteros de transporte; dirigibles, modernos y de principios de siglo; vehículos de lanzamiento espacial (en órbita baja); Camiones soviéticos de los años 60; camiones mineros modernos; camiones modernos de Rusia, Estados Unidos, China e India; coches eléctricos y scooters; trenes (con rieles); portacontenedores nucleares; portacontenedores y buques de carga (no petroleros); navegando buques de carga de los siglos 17-20; cintas transportadoras para la transferencia de minerales; Tractor Nassovsky para la exportación de misiles al inicio; y finalmente carros tirados por caballos.

Si ingresa el valor de Q , definido como la masa de la carga transportada en relación con la masa seca del vehículo, entonces esto es lo que parece para cada uno de los grupos:



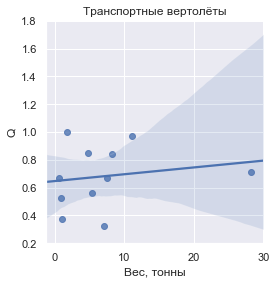
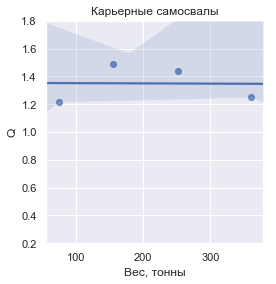
En números, los valores Q son:

Clase de activo	Q promedio	Desviación estándar Q
Aviones de carga	0.667091	± 0.206162
Helicópteros de transporte	0.681605	± 0.225062
Dirigibles, modernos y de principios de siglo	0.842673	± 0.374622
Vehículos de lanzamiento espacial (órbita baja)	0.372446	± 0.155810
Camiones soviéticos de los años 60	0.777435	± 0.232425
Camiones mineros modernos	1.349610	± 0.136840
Camiones modernos de Rusia, Estados Unidos, India, China	1.293679	± 0,604313
Tarjetas electricas y scooters	1.098433	± 0.343791
Tren (con rieles)	2.275989	± 0.205999
Portacontenedores nucleares	1.035233	± NA
Portacontenedores marítimos y buques de carga (no petroleros)	2.556004	± 0.378040
Veleros de carga de los siglos 17-20	2.488461	± 0,671785
Cintas transportadoras de carga	3.703704	± NA
Tractor Nasovsky para el lanzamiento de misiles	2.355919	± 0.525174
Carritos tirados por caballos	1.203061	± 0.389183

Como se puede ver, Q, aunque no en todas partes es estrictamente singular, pero dentro de cada grupo tiende a un valor común cercano a la unidad.


Me pareció ... misterioso. ¿Por qué un velero de madera, un automóvil eléctrico de aluminio y un portacontenedores atómico que contiene cien mil automóviles eléctricos aumentan su peso más o menos? ¿Qué nos hace crear vehículos con calidad Q ≈ 1 en masas que difieren miles de veces? ¿Es esta una manifestación de las propiedades de la física mundial, la economía terrestre, es una limitación de la inteligencia humana? ¿Cuán universal es esta ley? ¿Se implementará para civilizaciones de otras estrellas? Problemas globales. Es poco probable que se resuelvan aquí y ahora. Pero aquí es posible y necesario considerar y morder cuánto resultará. Esto es lo que haremos.

El récord mundial ^{[ 180 ] de} levantar una barra por una persona de peso promedio supera los 200 kg. Teóricamente, esto significa que nuestro cuerpo tiene un margen de seguridad para cargas bruscas de al menos hasta Q = 2.5. Sin embargo, esto requiere fuerzas y entrenamiento tan exorbitantes que nunca se usa en las actividades cotidianas. Es más recomendable empacar azúcar en bolsas de 50 kilogramos, aunque esto requiere cuatro veces más cargadores o un andador. Tenga en cuenta que esta situación es el resultado de la evolución biológica, en la que el intelecto humano no participó (casi) y, por lo tanto, tiene una "coartada".

La física y la ingeniería por sí solas no prohíben altas Qs. Hay una turbobomba de hidrógeno para el motor Shuttle a mitad de vuelo, esa pequeña cosa a la derecha en la imagen, desarrolla 54 megavatios de potencia ^{[ 60 ]} con un peso total del vehículo de 350 kg:

[Crédito de la imagen: [ 10 ]]

Si, simplificando, evalúa Q por potencia por kilogramo de masa, entonces esto es 100 veces más alto que el de un automóvil decente. ¡Pero esto es casi como un cohete! Es más barato fabricar 100 automóviles con Q = 1 y transportar la carga con ellos, en lugar de tratar de "aprovechar" esta unidad en un carro con ruedas.

Tales consideraciones sugieren que las razones aquí son económicas. Además, no en el sentido estricto de economías y países específicos (porque nuestros dispositivos son generados por personas y sistemas muy diferentes), sino en el sentido de "conveniencia de los esfuerzos". La idoneidad es lo suficientemente universal como para, aparentemente, aplicarse a productos muy diferentes y en algún lugar incluso a animales.

_{El artículo fue escrito para el sitio https://habr.com . Al copiar, consulte la fuente. El autor del artículo es Evgeny Bobukh .}

Tratemos de investigar los límites de esta conveniencia cuantitativamente. Planteamos la pregunta: ¿cómo depende el costo de un dispositivo de masa fija de Q ? Aquí, por ejemplo, hay un camión volquete que pesa 10 toneladas, se necesitan 10 toneladas de carga. También queremos hacer una tonelada de 10 toneladas, pero quitando 20 toneladas ( Q = 2) o incluso 50 ( Q = 5). Al mismo nivel de desarrollo tecnológico, el mismo volumen de producción. Está claro que las cargas más altas aumentarán los requisitos para materiales (acero -> titanio?), Y para motores (otras temperaturas, presiones) e ingeniería (menos tolerancias de error, diseños más complicados). Claramente, a medida que Q crece, todo será más caro. Pero, ¿cuántas veces, en comparación con las diez toneladas?

Esta tarea, por supuesto, no es trivial. Sin embargo, se pueden obtener algunas estimaciones a partir de las consideraciones más generales. Lo que haremos ahora.

Introducimos la función C ( Q ). Describe el costo más bajo posible de un dispositivo con una eficiencia de Q , expresado en los costos de un dispositivo similar de la misma masa en Q = 1. ¿Qué se sabe al respecto?

1. C (1) = 1, por definición.

2. C ( Q ) es una función continua, al menos hasta que la diferencia de masa se mide por átomos por pieza. Intuitivamente, parece lo suficientemente suave como para tener los primeros derivados. Creo que podemos admitir (como con la mayoría de las funciones físicas) que generalmente es analítico.

3. C ( Q ) es una función estrictamente creciente. Cuanto mayor es la calidad de Q , más difícil es hacer la estructura y más costosa es. Es decir dC ( Q ) / dQ > 0 al menos para Q > 0.

4. Con Q mayor que aproximadamente 3, C ( Q ) comienza a aumentar más rápido que linealmente. Por qué Como vemos que es más barato para las personas fabricar tres camiones para diez toneladas con Q = 1 que uno para treinta con Q = 3. Resumiendo, escribimos: k * C (1) < C ( k ) para k > ≈3 - otro en palabras, C ( k ) crece más rápido que k , para k > ≈3.

5. De manera similar, dado que diez aviones con Q = 0.1 son claramente antieconómicos que uno con Q = 1 (porque construyen el segundo, no el primero), para k > ≈3 tenemos: k * C (1 / k )> C (1), o C (1 / k )> 1 / k .

6. El costo de la bomba del Shuttle sugiere que al menos hasta Q ~ 100 el valor de C ( Q ) no aumenta como exponente con un indicador significativo. De lo contrario, este TNA no costaría millones de dólares, sino algún tipo de $ 10 ²⁰ , y difícilmente lo hubiéramos logrado. Es decir C (100) está en algún lugar alrededor de 10 ³ - 10 ⁸ , pero no en absoluto 10 ¹⁵ .

7. ¿A qué es igual C (0)? Este es el costo del dispositivo, que aún puede moverse solo, pero no puede quitar ninguna carga. Obviamente, tal "camión" es más barato que un camión completo. Pero cuantas veces? La historia muestra que a veces en lugar de decenas o cientos. Han pasado unos 15 años desde el primer avión capaz de moverse solo ( Q = 0) hasta el transporte de mercancías por vía aérea. Desde los primeros autos de gasolina hasta camiones bastante decentes con Q = 1.5 ([ 120 ] + [ 130 ]), un poco más. Si este desarrollo fuera una complejidad increíble, difícilmente se habría completado tan rápido. En consecuencia, la dificultad de fabricación y el costo de un vehículo con Q = 0 no deberían ser completamente diferentes de los de Q = 1. Por lo tanto, esperamos que C ( 0 ) se encuentre entre 0.1 y 0.5.

8. ¿Tiene sentido esta función para Q negativa? Bastante! Un camión con Q = -0.5 es uno que solo se moverá si retira la mitad de su peso de una grúa torre. Y Q = -1: este es un carro que desarrolla tracción cero. Capaz de transportar carga solo si la lleva remolcada. Es decir, generalmente sin motor. Obviamente, su costo, si no es distinto de cero, es muy pequeño. Por lo tanto, ponga C (-1) ≈ 0.

9. ¿Y qué es C (-2)? ¡Este es el costo de un dispositivo que necesita ser levantado con al menos el doble de su peso para moverse! Sí, las áreas Q <-1 son anclas, cimientos, pilotes, frenos. Dispositivos que impiden el movimiento. Allí, por supuesto, hay una dinámica completamente diferente y sus propias leyes, pero al menos vemos que C ( Q ) no termina con una singularidad en Q <-1, y que en la región Q = -1 tiene un mínimo, y por lo tanto Un pequeño vecindario de este punto C ( Q ) debería comportarse como una parábola.

Por lo tanto, incompleto C ( Q ) se parece a esto:


Expandimos C ( Q ) en una serie de Taylor en el punto Q = -1:



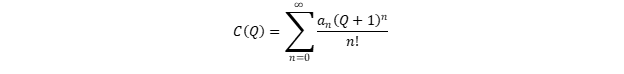
De la propiedad (8) se deduce que a ₀ = 0. Las propiedades (4), (5) y en parte (9) insinúan que un _{1 está} cerca de cero, o en cualquier caso, que su contribución no domina en el rango 0 .. .3.

Y luego resulta que el primer término distinto de cero en la expansión de C ( Q ) es parabólico, y que con Q en la región de las unidades C ( Q ) se comporta aproximadamente como una función cuadrática o un poco más rápida:

C ( Q ) ≈ a ₂ * ( Q +1) 2/2 + O (( Q + 1 ) ³ )

Y de [1] se deduce que un ₂ ≈ 1/2.

Finalmente, dado que al menos hasta Q ~ 100 la función C ( Q ) todavía no es exponencial (propiedad (6)), podemos ponerla allí igual a Q ^p con el exponente p en algún lugar en la región de 2 ... 4. Apenas más.

Conclusión: Para una masa fija, el costo del dispositivo C (Q) no aumenta más débil que (Q + 1) 2/4, pero no más rápido que aproximadamente O (Q ⁴ ) [1]

¿Es posible observar la dependencia real de C ( Q ) para comprender cuán correcta es esta conclusión? Es dificil La mayoría de los mecanismos creados por el hombre son masas diferentes, pero Q fijas en la región de la unidad. Necesitamos lo contrario: aproximadamente la misma masa, pero diferente Q. Al principio esperaba datos sobre motores de aviones ... pero el trabajo ^{[ 70 ] [ 80 ]} en sus precios es muy divertido. Los precios del motor se clasifican allí, y solo se publican las fórmulas de predicción y errores promedio.

Afortunadamente, la ayuda vino de los automóviles ^{[ 150 ]} . Es con ellos, con aproximadamente la misma masa, que se encuentran motores de varias capacidades. Y aunque la energía aún no es una carga transportable, con cierto esfuerzo de ingeniería es aproximadamente proporcional a ella. Lo que nos permite estimar si nuestra fórmula está cerca de la realidad.

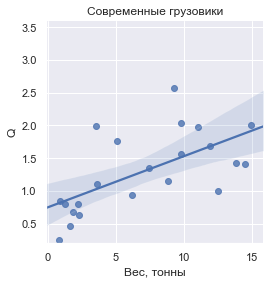
Parece que si:

[Fuente: [ 150 ]]

Los puntos azules son autos reales. En una primera aproximación, su precio aumenta como densidad de potencia en el grado de 2.3.

Puntos rojos: el precio calculado por la fórmula [1], basado en el supuesto de que Q = 1 corresponde a los automóviles más baratos por kilogramo en el rango de $ 20-30 mil. Se puede ver que la fórmula realmente da una buena estimación de C ( Q ) desde abajo (donde apuntamos).

Al observar la masa de estos sabrosos puntos, existe una fuerte tentación: extraer C ( Q ) a través de ellos y, por lo tanto, estudiar la dependencia directamente. Esto no se puede hacer. Principalmente porque el precio de un automóvil de pasajeros está determinado no solo por sus características de tracción. Es difícil imaginar un automóvil para cien kilobax que no tenga el mejor aire acondicionado, los asientos más cómodos y el "cenicero de platino con bisel chapado en rodio". Y todo esto cuesta dinero que no tiene nada que ver con nuestra C ( Q ). Sin embargo, aquí la "rama" inferior de los automóviles, que pasa casi exactamente de acuerdo con la C ( Q ) calculada, parece interesante. Me atrevo a admitir que estos son solo autos sin lujos. Donde "no damas, sino para ir". Pero más de aproximadamente $ 100K por un automóvil, estos ya no están allí.

_{El artículo fue escrito para el sitio https://habr.com . Al copiar, consulte la fuente. El autor del artículo es Evgeny Bobukh .}

Por lo tanto, podemos estimar el costo de los dispositivos con Q alta, al menos en orden de magnitud. ¿Por qué era esto necesario?

Pero por qué. Echa un vistazo al primer paso de la compañía espacial. Bueno, al menos Proton-M ^{[ 110 ]} , para concreción. Es un vehículo casi completo, con motores, un sistema de control, un margen de seguridad decente y un peso en seco de 31 toneladas. Al mismo tiempo, al comienzo del cohete, arrastra sobre su joroba no solo la carga útil, sino también todo el combustible, todas las etapas superiores y, por supuesto, sí mismo. En total - 683 toneladas. ¡Más sobrecarga de arranque, total (efectivo) 1068 toneladas de carga! Desde el punto de vista de la primera etapa, funciona en un modo terrible Q = (1068/31) = 34.4! Esto equivale a 50 toneladas de carga apiladas en un automóvil de pasajeros.

Y sabemos que el costo de un dispositivo con Q alta es al menos (Q + 1) 2/4 veces mayor que algo similar con Q ≈ 1. Para Proton, esto equivale a ... 313 veces.

Es decir, el Proton debería costar 300 veces más que un dispositivo similar con Q = 1. Y esta cifra depende poco del progreso y la tecnología. Tan pronto como los "científicos británicos" inventan una súper aleación que hace que un cohete sea más barato, los motores terrestres también se vuelven más baratos. Por lo tanto, un cohete químico, incluso reutilizable, siempre será muy costoso. Te guste o no.

Bueno Digamos 300 veces. ¿Pero comparado con qué ? ¿Sería bueno comparar nuestros cálculos con algunos dispositivos objetivamente existentes para eliminar errores graves?

Desafortunadamente, no hay misiles de treinta toneladas con Q = 1. Pero hay análogos aproximados adecuados para la comparación:

• El primero es un camión minero. Sí, no un cohete Pero aún así, también es un motor térmico, no una ingeniería completamente trivial, y uno de los medios más baratos para transportar mercancías. Y si ya estamos hablando de exploración espacial, ¿no debería ser el camión el prototipo del modelo de negocio de la cabina espacial? Entonces, intentemos, al menos para una estimación general. Aquí hay un Belaz-7540 de 30 toneladas. El precio de mercado ^{[ 140 ]} es de 3,7 millones de rublos, es decir $ 62K. Para Proton, esto se convierte en el costo de la primera etapa en la región de $ 19 millones. Wikipedia representa ^{[ 100 ] el} costo inicial como $ 65 millones. Bastante cerca, dado que esta cantidad incluye mucho más, excepto por el precio del primer paso.
• En [ 160 ] se describe una plataforma experimental de cohetes sobre rieles. Una masa de 10 toneladas, cinco pasos, acelera a 4 km / s. El precio es de 750 kilobax. A juzgar por las imágenes y los parámetros publicados, este dispositivo funciona en algún lugar con Q = 10. No es una unidad, pero aún no es 34. Si comienza con estos números, el primer paso del Proton debería costar alrededor de $ 23 millones.
• En general, cuando trato de imaginar un cohete con Q = 1, en mi mente hay una especie de espacio en blanco fuerte con una pequeña muesca llena de pólvora. La pólvora se quema y empuja el blanco hacia adelante. Bastante, no acelerarás tanto. Aplasté esta imagen durante dos días, hasta que me di cuenta de que me recuerda. Esto es ... ¡un martillo neumático! Donde el gas se expande y empuja el espacio en blanco. La última bastardización de la idea de un motor a reacción, conservando algún tipo de parentesco. Bueno, lo estamos buscando. Sí, aquí está el martillo neumático Stanko M212 ^{[ 170 ]} . El peso del disco es de 2 toneladas, toda la estructura es de 58,3 toneladas. El sistema Q , por lo tanto, es un modesto 0.034. Vendido por 40 mil euros. Si extrapolamos el costo de esta broma a Q = 34.4 de acuerdo con la fórmula [1], obtenemos ... 47 millones de euros. O 24 millones en proporción de más de 30 toneladas.

Parece que no estamos realmente divorciados de la realidad.

Para resumir. Dado que los cohetes, incluso los reutilizables, cuestan 2–3 órdenes de magnitud más caras que los camiones, cualquier asentamiento espacial hecho con materiales terrestres también costará 100–1,000 veces más que sus contrapartes terrestres. Esta es una barrera muy alta para el desarrollo.

Los misiles son caros porque son muy pesados ​​y se ven obligados a trabajar cuando no son saludables a altas Q. ¿Pero por qué son pesados ​​los cohetes? La respuesta (que es algo más profunda que la fórmula Tsiolkovsky) la consideraremos en la segunda parte.

Continuará

Actualización: varias personas trataron de señalar las ambigüedades con respecto al combustible al considerar los misiles. Lo pensé Y me di cuenta de que realmente hay cierta inexactitud en el artículo. Visto en los comentarios aquí .