Estimación de la orientación espacial, o Cómo no temer a los filtros de Mahoney y Majwik

De que estamos hablando

La aparición en Habre de una publicación sobre el filtro Majwik fue un evento simbólico a su manera. Aparentemente, el entusiasmo general por los drones revivió el interés en la tarea de evaluar la orientación del cuerpo mediante mediciones inerciales. Al mismo tiempo, los métodos tradicionales basados ​​en el filtro de Kalman dejaron de satisfacer al público, ya sea por los altos requisitos de recursos informáticos que eran inaceptables para los drones o por la configuración compleja y poco intuitiva.

La publicación fue acompañada por una implementación muy compacta y eficiente del filtro en C. Sin embargo, a juzgar por los comentarios, el significado físico de este código, así como el artículo completo, permaneció vago para algunos. Bueno, admitimos sinceramente: el filtro Majwik es el más complejo del grupo de filtros basado en general en principios muy simples y elegantes. Consideraré estos principios en mi publicación. El código no estará aquí. Mi publicación no es una historia sobre una implementación específica del algoritmo de estimación de orientación, sino más bien una invitación a inventar sus propias variaciones sobre un tema determinado, que puede ser mucho.

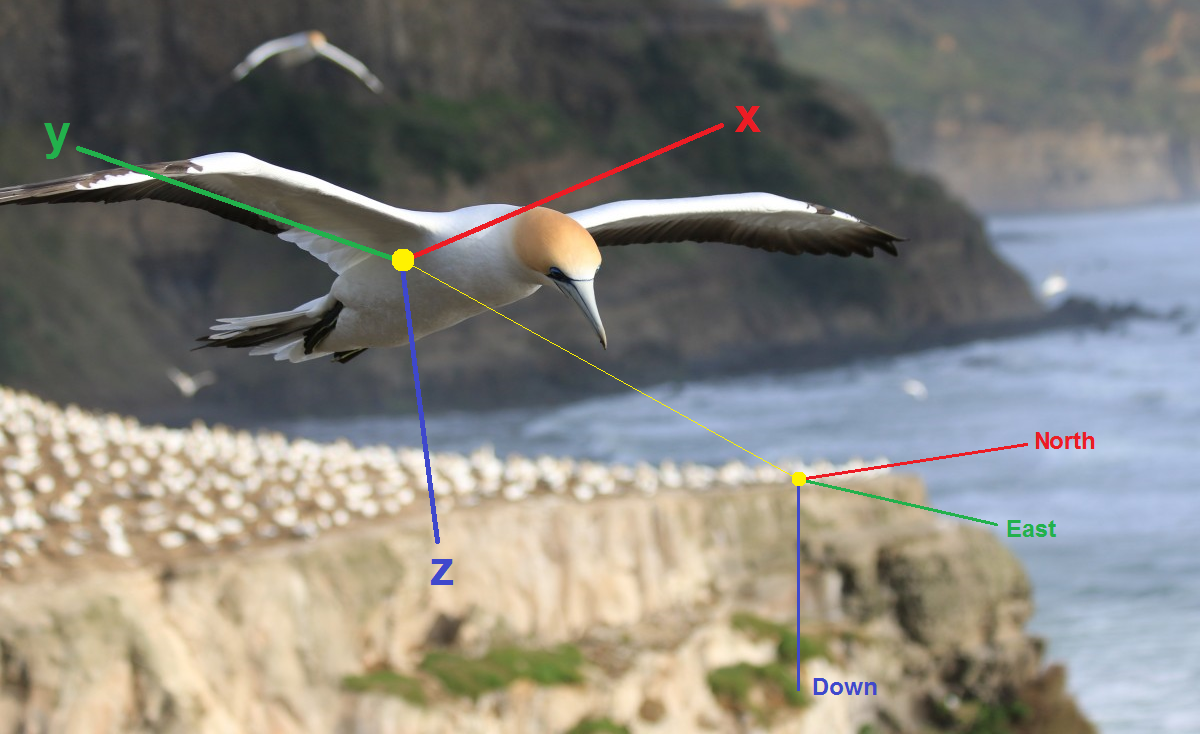
Vista de orientación

Recordemos lo básico. Para evaluar la orientación del cuerpo en el espacio, primero debe seleccionar algunos parámetros que juntos determinen de manera única esta orientación, es decir. esencialmente la orientación del sistema de coordenadas asociado $$$xyz$ sistema relativamente condicionalmente fijo, por ejemplo, el sistema geográfico NED (Norte, Este, Abajo). Entonces necesitas hacer ecuaciones cinemáticas, es decir expresa la tasa de cambio de estos parámetros a través de la velocidad angular de los giroscopios. Finalmente, uno necesita introducir mediciones vectoriales de acelerómetros, magnetómetros, etc. en el cálculo. Estas son las formas más comunes de representar la orientación:

Ángulos de Euler - roll (roll, $$$\ phi$ ), tono (tono, $$$\ theta$ ), curso (título, $$$\ psi$ ) Este es el conjunto de parámetros de orientación más intuitivo y conciso: el número de parámetros es exactamente igual al número de grados de libertad de rotación. Para estos ángulos, podemos escribir las ecuaciones cinemáticas de Euler . Son muy aficionados a la mecánica teórica, pero en problemas de navegación son de poca utilidad. En primer lugar, conocer los ángulos no permite convertir directamente los componentes de cualquier vector de un sistema de coordenadas conectado a un geográfico o viceversa. En segundo lugar, a una inclinación de ± 90 grados, las ecuaciones cinemáticas se degeneran, el balanceo y el rumbo se vuelven indefinidos.

Matriz de rotación - Matriz $$$\ mathbf {C}$ Tamaño 3 × 3, por el cual debe multiplicar cualquier vector en el sistema de coordenadas asociado para obtener el mismo vector en el sistema geográfico: $$$\ mathbf {r} _ {NED} = \ mathbf {C} \ mathbf {r} _ {xyz}$ . La matriz siempre es ortogonal, es decir. $$$\ mathbf {C} = \ mathbf {C} ^ {T}$ . La ecuación cinemática tiene la forma $$$\ dot {\ mathbf {C}} = \ mathbf {C} \ mathbf {\ Omega}$ .
Aqui $$$\ mathbf {\ Omega}$ - una matriz de componentes de velocidad angular medida por giroscopios en un sistema de coordenadas conectado:

$$

$$\ mathbf {\ Omega} = \ begin {bmatrix} 0 & - \ omega_ {z} & \ omega_ {y} \\ \ omega_ {z} & 0 & - \ omega_ {x} \\ - \ omega_ {y } & \ omega_ {x} & 0 \\ \ end {bmatrix}$$

La matriz de rotación es un poco menos obvia que los ángulos de Euler, pero a diferencia de ellos, le permite convertir vectores directamente y no pierde significado en ninguna posición angular. Desde el punto de vista computacional, su principal inconveniente es la redundancia: en aras de tres grados de libertad, se introducen nueve parámetros a la vez, y todos ellos deben actualizarse de acuerdo con la ecuación cinemática. El problema puede simplificarse ligeramente utilizando la ortogonalidad de la matriz.

El cuaternión de rotación es un remedio radical pero muy poco intuitivo contra la redundancia y la degeneración. Este es un objeto de cuatro componentes. $$$\ mathbf {q} = q_ {0} + q_ {1} \ mathbf {i} + q_ {2} \ mathbf {j} + q_ {3} \ mathbf {k}$ - ni un número, ni un vector, ni una matriz. El cuaternión se puede ver desde dos ángulos. Primero, ¿qué hay de la cantidad formal del escalar? $$$q_ {0}$ y vector $$$q_ {1} \ mathbf {i} + q_ {2} \ mathbf {j} + q_ {3} \ mathbf {k}$ donde $$$\ mathbf {i}, \ mathbf {j}, \ mathbf {k}$ - vectores de eje unitario (que, por supuesto, suena absurdo). En segundo lugar, como una generalización de números complejos, donde ahora usamos no una, sino tres unidades imaginarias diferentes $$$\ mathbf {i}, \ mathbf {j}, \ mathbf {k}$ (lo que no suena menos absurdo). ¿Cómo se relaciona un cuaternión con un giro? A través del teorema de Euler: un cuerpo siempre se puede transferir de una orientación dada a otra con una rotación finita en algún ángulo $$$\ alpha$ alrededor de algún eje con un vector guía $$$\ mathbf {u}$ . Estos ángulos y ejes se pueden combinar en un cuaternión: $$$\ mathbf {q} = \ mathrm {cos} (\ alpha / 2) + \ mathbf {u} \ mathrm {sin} (\ alpha / 2)$ . Al igual que una matriz, un cuaternión se puede usar para convertir directamente cualquier vector de un sistema de coordenadas a otro: $$$\ mathbf {r} _ {NED} = \ mathbf {q} \ mathbf {r} _ {xyz} {\ mathbf {q}} ^ {- 1}$ . Como puede ver, la representación de la orientación del cuaternión también sufre redundancia, pero mucho menos que la matriz: un parámetro adicional es solo uno. La revisión exhaustiva de los cuaterniones ya estaba en Habré . Hablaron de geometría y gráficos en 3D. También estamos interesados ​​en la cinemática, ya que la tasa de cambio del cuaternión debe estar relacionada con la velocidad angular medida. La ecuación cinemática correspondiente tiene la forma $$$\ dot {\ mathbf {q}} = 1/2 \ mathbf {q} \ mathbf {\ omega}$ donde esta el vector $$$\ mathbf {\ omega}$ También se considera un cuaternión con una parte escalar cero.

Esquemas de filtro

El enfoque más ingenuo para calcular la orientación es armarse con una ecuación cinemática y actualizar de acuerdo con ella cualquier conjunto de parámetros que nos guste. Por ejemplo, si elegimos una matriz de rotación, podemos escribir un ciclo con algo en el espíritu de C += * Omega * dt . El resultado será decepcionante. Los giroscopios, especialmente los MEMS, tienen compensaciones cero grandes e inestables; como resultado, incluso en reposo completo, la orientación calculada tendrá un error de acumulación ilimitado (deriva). Todos los trucos inventados por Mahoney, Majwick y muchos otros, sin excluirme, tenían como objetivo compensar esta deriva al involucrar mediciones de acelerómetros, magnetómetros, receptores GNSS, retrasos, etc. Así nació una familia completa de filtros de orientación, basada en un principio básico simple.

Principio basico. Para compensar la deriva de orientación, es necesario agregar a la velocidad angular medida por giroscopios una velocidad angular de control adicional construida sobre la base de mediciones vectoriales de otros sensores. El vector de velocidad angular de control debe esforzarse por combinar las direcciones de los vectores medidos con sus direcciones verdaderas conocidas.

Aquí se adopta un enfoque completamente diferente que al construir el término de corrección del filtro de Kalman. La principal diferencia es que la velocidad angular de control no es un término, sino un factor para el valor estimado (matriz o cuaternión). De esto se derivan importantes ventajas:

• Se puede construir un filtro de evaluación para la orientación en sí, y no para pequeñas desviaciones de la orientación de la proporcionada por los giroscopios. Además, los valores estimados satisfarán automáticamente todos los requisitos que impone la tarea: la matriz será ortogonal, el cuaternión normalizado.
• El significado físico de la velocidad angular de control es mucho más claro que el término de corrección en el filtro de Kalman. Todas las manipulaciones se realizan con vectores y matrices en el espacio físico tridimensional ordinario, y no en un espacio de estado multidimensional abstracto. Esto simplifica enormemente el refinamiento y el ajuste del filtro y, como beneficio adicional, le permite deshacerse de las matrices de gran dimensión y las bibliotecas de matrices pesadas.

Ahora veamos cómo se implementa esta idea en opciones de filtro específicas.

Filtro Mahoney. Toda la matemática furiosa del artículo original de Mahoney fue escrita para justificar ecuaciones simples (32). Los reescribimos en nuestra notación. Si ignoramos la estimación de los desplazamientos cero de los giroscopios, quedan dos ecuaciones clave: la ecuación cinemática de la matriz de rotación en sí (con la velocidad angular de control en forma de matriz $$$\ mathbf {\ Omega} '$ ) y la ley de la formación de esta misma velocidad en forma de vector $$$\ mathbf {\ omega} '$ . Por simplicidad, asumimos que no hay aceleraciones o pastillas magnéticas, y gracias a esto, las mediciones de aceleración de caída libre están disponibles para nosotros. $$$- \ hat {\ mathbf {g}} _ {xyz}$ de acelerómetros y el campo magnético de la Tierra $$$\ hat {\ mathbf {m}} _ {xyz}$ de magnetómetros. Ambos vectores son medidos por sensores en un sistema de coordenadas conectado, y en el sistema geográfico se conoce su posición: $$$- \ mathbf {g} _ {NED}$ apuntando hacia arriba $$$\ mathbf {m} _ {NED}$ - Al norte magnético. Entonces las ecuaciones de filtro de Mahoney se verán así:

$$

$$\ dot {\ mathbf {C}} = \ mathbf {C} (\ mathbf {\ Omega} + \ mathbf {\ Omega} ') \\ \ mathbf {\ omega'} = k_ {g} \ hat {\ mathbf {g}} _ {xyz} \ times \ mathbf {C} ^ {T} \ mathbf {g} _ {NED} + k_ {m} \ hat {\ mathbf {m}} _ {xyz} \ times \ mathbf {C} ^ {T} \ mathbf {m} _ {NED}$$

Miremos cuidadosamente la segunda ecuación. El primer término en el lado derecho es un producto vectorial. El primer factor es la aceleración medida de la gravedad, el segundo es cierto. Dado que los factores deben estar en un sistema de coordenadas, el segundo factor se convierte en un sistema conectado multiplicando por $$$\ mathbf {C} ^ {T}$ . La velocidad angular, construida como un producto vectorial, es perpendicular al plano de los vectores de factores. Le permite rotar la posición estimada del sistema de coordenadas asociado hasta que los vectores de factores coincidan en la dirección; luego, el producto vectorial se restablecerá a cero y la rotación se detendrá. Coeficiente $$$k_ {g}$ establece la rigidez de tal retroalimentación. El segundo término realiza una operación similar con un vector magnético. De hecho, el filtro de Mahoney encarna la tesis bien conocida: el conocimiento de dos vectores no colineales en dos sistemas de coordenadas diferentes le permite restaurar de manera única la orientación mutua de estos sistemas. Si hay más de dos vectores, esto proporcionará una redundancia de medición útil. Si solo hay un vector, entonces un grado de libertad rotacional (movimiento alrededor de este vector) no puede ser reparado. Por ejemplo, si solo se da un vector $$$- \ mathbf {g}$ , entonces puede ajustar la deriva del roll y pitch, pero no el curso.

Por supuesto, el filtro Mahoney no tiene que usar una matriz de rotación. También hay variantes de quaternion no canónicas.

Plataforma virtual de giroscopio. En el filtro Mahoney, aplicamos el control de velocidad angular $$$\ mathbf {\ omega '}$ al sistema de coordenadas asociado. Pero puede aplicarlo a la posición estimada del sistema de coordenadas geográficas. La ecuación cinemática toma la forma.

$$

$$\ dot {\ mathbf {C}} = \ mathbf {C} \ mathbf {\ Omega} - \ mathbf {\ Omega} '\ mathbf {C}$$

Resulta que este enfoque allana el camino para analogías físicas muy fructíferas. Es suficiente recordar con qué comenzó la técnica giroscópica: los sistemas de navegación vertical e inercial basados ​​en una plataforma estabilizada por giro en un cardán.


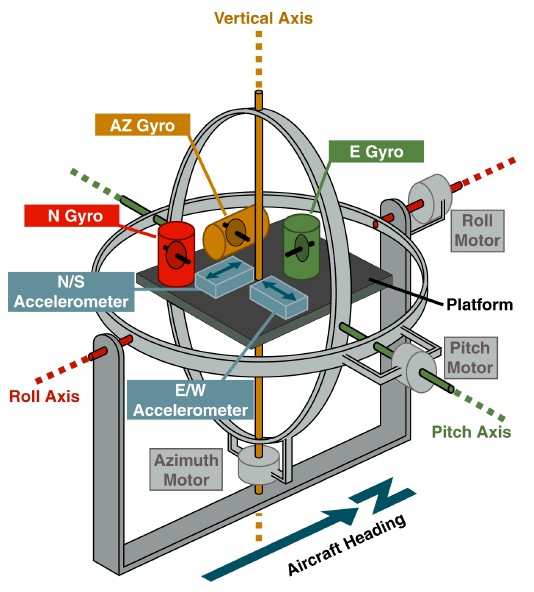www.theairlinepilots.com

El objetivo de la plataforma allí era la materialización del sistema de coordenadas geográficas. La orientación del portador se midió en relación con esta plataforma mediante sensores de ángulo en los marcos de suspensión. Si los giroscopios tenían una deriva, entonces la plataforma también se desplazaba detrás de ellos, y se acumulaban errores en las lecturas de los sensores de ángulo. Para eliminar estos errores, se introdujeron los comentarios de los acelerómetros instalados en la plataforma. Por ejemplo, la desviación de la plataforma desde el horizonte alrededor del eje norte fue percibida por el acelerómetro del eje este. Esta señal permitió configurar la velocidad angular de control $$$\ mathbf {\ omega '}$ devolviendo la plataforma al horizonte.

Podemos usar los mismos conceptos visuales en nuestra tarea. La ecuación cinemática descrita debe leerse de la siguiente manera: la tasa de cambio de orientación es la diferencia entre dos movimientos de rotación: el movimiento absoluto de la portadora (el primer término) y el movimiento absoluto de la plataforma giroscópica virtual (el segundo término). La analogía puede extenderse a la ley de formación de la velocidad angular de control. Vector $$$- \ hat {\ mathbf {g}} _ {NED} = - \ mathbf {C} \ hat {\ mathbf {g}} _ {xyz}$ Representa el testimonio de acelerómetros, supuestamente parados en una plataforma giroscópica. Luego, por razones físicas, puede escribir:

$$

$$\ omega '_ {N} = - gk_ {g} \ hat {g} _ {E}, \; \ omega '_ {E} = gk_ {g} \ hat {g} _ {N}$$

Sería posible llegar exactamente al mismo resultado de una manera formal, haciendo la multiplicación de vectores en el espíritu del filtro Mahoney, pero ahora no en un sistema de coordenadas geográficas, sino conectado. ¿Es solo necesario?

El primer indicio de una útil analogía entre la plataforma y la navegación inercial de correaje aparece, aparentemente, en la antigua patente de Boeing . Luego, esta idea fue desarrollada activamente por Salychev , y recientemente, por mí también . Las ventajas obvias de este enfoque:

• La velocidad angular de control se puede formar sobre la base de principios físicos comprensibles.
• Naturalmente, los canales horizontales y direccionales, que son muy diferentes en sus propiedades y métodos de corrección, están separados. En el filtro Mahoney se mezclan.
• Es conveniente compensar el efecto de las aceleraciones debido al uso de datos GNSS, que se emiten precisamente en ejes geográficos en lugar de relacionados.
• Es fácil generalizar el algoritmo para el caso de la navegación inercial de alta precisión, donde hay que tener en cuenta la forma y la rotación de la Tierra. Cómo hacer esto en el esquema de Mahoney, no me lo puedo imaginar.

Filtro Majwick. Majwik eligió el camino difícil . Si Mahoney, aparentemente, intuitivamente tomó su decisión, y luego la justificó matemáticamente, entonces Majwik desde el principio demostró ser un formalista. Se comprometió a resolver el problema de optimización. Razonó así. Establecer la orientación del cuaternión de rotación. En el caso ideal, la dirección calculada de algún vector medido (tengamos esto $$$- \ mathbf {g}$ ) coincide con el verdadero. Entonces será $$${\ mathbf {q}} ^ {- 1} \ mathbf {g} _ {NED} \ mathbf {q} = \ hat {\ mathbf {g}} _ {xyz}$ . En realidad, esto no siempre se puede lograr (especialmente si hay más de dos vectores), pero puede intentar minimizar la desviación $$$\ mathbf {F} = {\ mathbf {q} ^ {- 1} \ mathbf {g} _ {NED} \ mathbf {q}} - \ hat {\ mathbf {g}} _ {xyz}$ de la igualdad exacta Para hacer esto, presentamos el criterio de minimización

$$

$$E = \ frac {1} {2} | \ mathbf {F} | ^ {2} \ rightarrow \ mathrm {min}$$

La minimización requiere un descenso de gradiente: moverse en pequeños pasos en la dirección opuesta al gradiente $$$\ nabla E$ es decir opuesto al aumento más rápido de la función $$$E$ . Por cierto, Majwik comete un error: en todas sus obras no presenta $$$E$ y escribe insistentemente $$$\ nabla \ mathbf {F}$ en lugar de $$$\ nabla E$ , aunque en realidad calcula exactamente $$$\ nabla E$ .

Como resultado, el descenso del gradiente conduce a la siguiente condición: para compensar la deriva de orientación, se debe agregar un nuevo término negativo proporcional a la ecuación cinemática a partir de la ecuación cinemática $$$\ nabla E$ :

$$

$$\ dot {\ mathbf {q}} = \ frac {1} {2} \ mathbf {q} \ mathbf {\ omega} - \ beta \ frac {\ nabla E} {| \ nabla E |}$$

Aquí, Majwik se aleja un poco de nuestro "principio básico": no agrega el término de corrección a la velocidad angular, sino a la tasa de cambio del cuaternión, que no es exactamente lo mismo. Como resultado, puede resultar que el cuaternión actualizado deje de ser único y, en consecuencia, pierda la capacidad de representar la orientación. Por lo tanto, para el filtro Majwik, la normalización artificial del cuaternión es una operación vital, mientras que para otros filtros es deseable, no opcional.

El efecto de la aceleración.

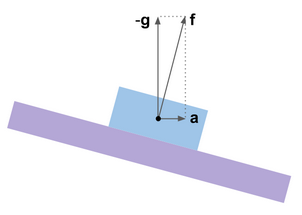
Hasta ahora, se suponía que no hay aceleraciones verdaderas y los acelerómetros solo miden la aceleración gravitacional $$$- \ mathbf {g}$ . Esto hizo posible obtener un estándar vertical y, con su ayuda, compensar el desplazamiento de balanceo y cabeceo. Sin embargo, en el caso general, los acelerómetros, independientemente de su principio operativo, miden la aceleración aparente : la diferencia vectorial de la aceleración verdadera y la aceleración gravitacional $$$\ mathbf {f} = \ mathbf {a} - \ mathbf {g}$ . La dirección de la aceleración aparente no coincide con la vertical, y los errores causados ​​por las aceleraciones aparecen en las estimaciones de balanceo y cabeceo.

Esto es fácil de ilustrar utilizando la analogía de una plataforma virtual de giroscopio. Su sistema de corrección está diseñado para que la plataforma se detenga en esa posición angular en la que las señales de los acelerómetros, supuestamente instalados en él, se restablecen a cero, es decir. cuando el vector medido $$$\ mathbf {f}$ se vuelve perpendicular a los ejes de la sensibilidad de los acelerómetros. Si no hay aceleración, esta posición coincide con el horizonte. Cuando ocurren aceleraciones horizontales, la plataforma giroscópica se desvía. Podemos decir que la plataforma giroscópica es similar a un péndulo o línea de plomada fuertemente amortiguada.



En los comentarios a la publicación sobre el filtro Majwik, surgió una pregunta sobre si es posible esperar que este filtro sea menos susceptible a las aceleraciones que, por ejemplo, el filtro Mahoney. Por desgracia, todos los filtros descritos aquí explotan los mismos principios físicos y, por lo tanto, sufren los mismos problemas. Es imposible engañar a la física con las matemáticas. ¿Qué hacer entonces?

La forma más simple y difícil fue inventada a mediados del siglo pasado para los giroscopios de aviación: para reducir o poner a cero completamente la velocidad angular de control en presencia de aceleraciones o la velocidad angular del recorrido (que indica la entrada en un giro). El mismo método se puede aplicar a los sistemas de plataforma actuales. En este caso, las aceleraciones deben juzgarse por los valores $$$\ hat {f} _ {N}, \ hat {f} _ {E}$ pero no $$$\ hat {f} _ {x}, \ hat {f} _ {y}$ que a su vez son cero. Sin embargo en tamaño $$$\ hat {\ mathbf {f}} _ {NED}$ No siempre es posible distinguir las verdaderas aceleraciones de las proyecciones de aceleración gravitacional, que se debe a la inclinación de la plataforma giroscópica, que debe eliminarse. Por lo tanto, el método no funciona de manera confiable, pero no requiere sensores adicionales.

Un método más preciso se basa en el uso de mediciones de velocidad externas desde el receptor GNSS. Si se conoce la velocidad $$$\ mathbf {v}$ , entonces se puede diferenciar numéricamente y obtener una verdadera aceleración $$$\ dot {\ mathbf {v}}$ . Entonces la diferencia $$$\ hat {\ mathbf {f}} _ {NED} - \ dot {\ mathbf {v}}$ será exactamente igual $$$- \ hat {\ mathbf {g}} _ {NED}$ independientemente del movimiento de los medios. Se puede utilizar como estándar de vertical. Por ejemplo, puede especificar la velocidad angular de control de la plataforma giroscópica en el formulario

$$

$$\ omega '_ {N} = gk_ {g} (\ hat {f} _ {E} - \ dot {v} _ {E}), \; \ omega '_ {E} = - gk_ {g} (\ hat {f} _ {N} - \ dot {v} _ {N})$$

Compensación cero del sensor

Una característica triste de los giroscopios y acelerómetros de grado de consumo es la gran inestabilidad de cero compensaciones en tiempo y temperatura. Para eliminarlos, solo la calibración de fábrica o de laboratorio no es suficiente; debe reevaluar durante la operación.

Giroscopios. Trataremos con cero compensaciones de giroscopios $$$\ delta {\ mathbf {\ omega}}$ . La posición estimada del sistema de coordenadas asociado se aleja de su posición real con una velocidad angular determinada por dos factores opuestos: cero desplazamientos de los giroscopios y control de la velocidad angular: $$$\ delta {\ mathbf {\ omega}} - \ mathbf {\ omega '}$ . Si el sistema de corrección (por ejemplo, en el filtro Mahoney) logró detener la salida, entonces en el estado estable será $$$\ delta {\ mathbf {\ omega}} = \ mathbf {\ omega '}$ . En otras palabras, en el control de velocidad angular $$$\ mathbf {\ omega '}$ información sobre una perturbación válida desconocida $$$\ delta {\ mathbf {\ omega}}$ . Por lo tanto, se puede aplicar una estimación compensatoria : no conocemos la magnitud de la perturbación directamente, sin embargo, sabemos qué acción correctiva es necesaria para equilibrarla. Esta es la base para estimar los desplazamientos cero de los giroscopios. Por ejemplo, en Mahoney, la puntuación se actualiza de acuerdo con la ley

$$

$$\ dot {\ hat {\ delta \ mathbf {\ omega}}} = k_ {b} \ mathbf {\ omega '}$$

Sin embargo, el resultado es extraño: las estimaciones alcanzan 0.04 rad / s. Tal inestabilidad de las compensaciones cero no se produce incluso en los giroscopios más desagradables. Sospecho que el problema es que Mahoney no usa GNSS u otros sensores externos, y está completamente afectado por la influencia de las aceleraciones. Solo en el eje vertical, donde la aceleración no daña, la estimación parece más o menos robusta:


Mahony et al., 2008

Acelerómetros Acelerómetros de compensación de velocidad cero $$$\ delta {\ mathbf {f}}$ Mucho más difícil. La información sobre ellos debe extraerse del mismo control de velocidad angular $$$\ mathbf {\ omega '}$ . Sin embargo, en movimiento rectilíneo, el efecto del desplazamiento cero de los acelerómetros es indistinguible de la inclinación del portador o de la inclinación de la instalación del bloque sensor en él. Sin aditivos para $$$\ mathbf {\ omega '}$ Los acelerómetros no crean. El aditivo aparece solo por turnos, lo que nos permite separar y evaluar independientemente los errores de giroscopios y acelerómetros. Un ejemplo de cómo se puede hacer esto está en mi artículo . Aquí están las fotos de allí:

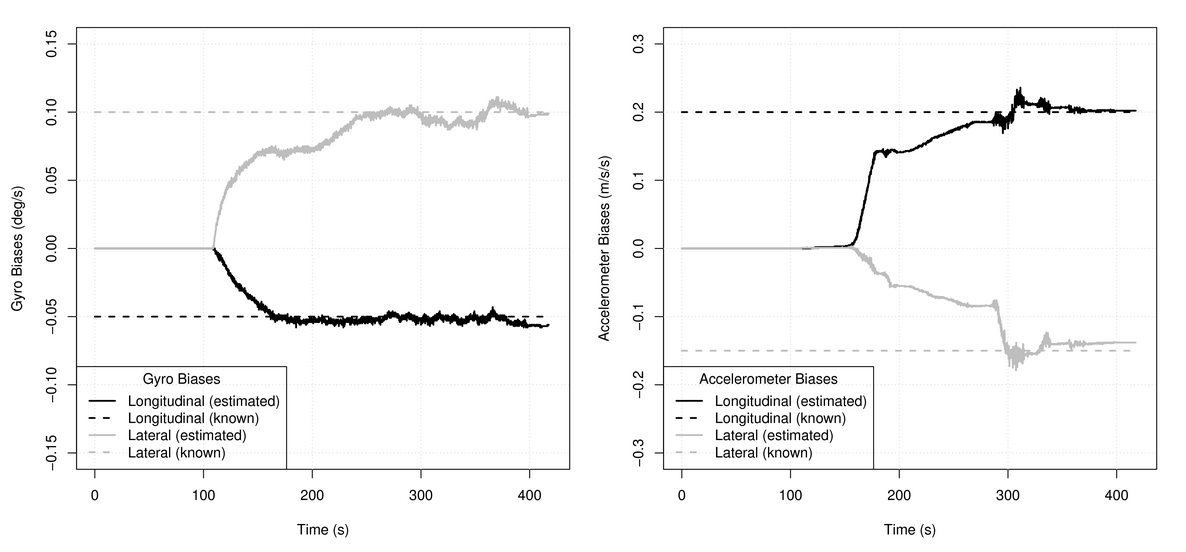
En lugar de una conclusión: ¿qué pasa con el filtro de Kalman?

No tengo dudas de que los filtros descritos aquí casi siempre tendrán una ventaja sobre el filtro tradicional de Kalman en términos de velocidad, compacidad del código y facilidad de configuración, para esto fueron creados. En cuanto a la precisión de la evaluación, aquí no todo está tan claro. Conocí los filtros Kalman diseñados sin éxito, que en precisión eran notablemente inferiores a un filtro con una plataforma de giroscopio virtual. Majwik también demostró los beneficios de su filtro en relación con algunas estimaciones de Kalman. Sin embargo, para la misma tarea de estimación de orientación, puede construir al menos una docena de circuitos de filtro Kalman diferentes, y cada uno tendrá innumerables configuraciones. No tengo ninguna razón para pensar que el filtro Mahoney o Majwik será más preciso que el mejor filtro Kalman posible . Y, por supuesto, el enfoque de Kalman siempre tendrá la ventaja de la universalidad: no impone restricciones estrictas sobre las propiedades dinámicas específicas del sistema evaluado.