Parte 2. Combustible muy pesado
Parte anterior 1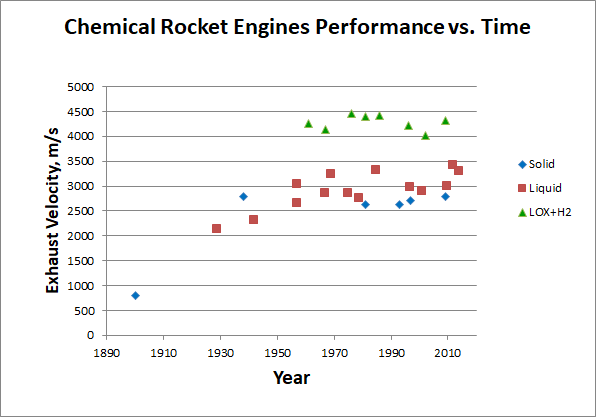
Ante ti está la Estación Espacial Internacional. Con una masa de 420 toneladas y un valor de
[ 20 ] de $ 150 mil millones:

Su energía cinética, la buena
E =
mv 2/2 , es 1.3 * 10
13 julios. Agregando energía potencial a una altitud de 400 kilómetros, obtenemos 1.4 * 10
13 J.
¿Cuánto gas necesitas quemar para obtener esta energía? Resulta que no tanto. 350 toneladas en total. Este es aproximadamente el
[ 200 ] presupuesto de energía de un día de Ulan-Ude.
¿Cómo es que lejos de la ciudad más rica del mundo en un solo día maneja la energía suficiente para acelerar la EEI a la velocidad orbital, sin embargo, tenemos una estación para todo el mundo y cuesta dinero excesivamente loco?
La respuesta
radica en lo obvio de la anatomía del vehículo de lanzamiento.
El transportista, como mínimo, debe incluir:
- Carga útil De lo contrario, ¿por qué es necesario?
- Al menos un motor.
- Una vivienda que conecta todo esto.
- Y, por supuesto, combustible. Como fluido de trabajo y, en la mayoría de los casos, como fuente de energía.
Y en el último párrafo, el problema está enraizado. Para subir y arrastrar un cierto mínimo de combustible, necesita ... correctamente, ¡combustible adicional! En el aumento de los cuales también necesita combustible! Y esta envoltura dura mucho tiempo. Por supuesto, converge, de lo contrario no volaríamos a ningún lado. Pero de acuerdo con los resultados de la convergencia, un cohete moderno, incluso de múltiples etapas, incluso de alta calidad, diseñado y ejecutado, en masa se compone principalmente de este mismo combustible.
Bueno, aquí hay un ejemplo de libro de texto, Saturno V no es el más nuevo, sino uno de los misiles más efectivos de la historia
[ 30 ] :

[Imagen original de la historia de la NASA [
40 ]]
Peso inicial: 2970 toneladas. Unos 2670 de ellos son combustible. De los cuales 2160 se queman en menos de tres minutos de toda la expedición lunar. A pesar de que la energía cinética de la carga útil en órbita "cuesta" solo 100 toneladas de combustible.
Resulta que la principal dificultad para entrar en órbita no es la falta de energía. Sus terrícolas tienen suficiente energía cinética no solo para las estaciones, sino incluso para los cruceros en órbita. El problema es diferente: nuestro combustible es demasiado pesado. Se necesita demasiado en kilogramos para recolectar la cantidad de energía requerida para el vuelo. ¿Por qué la mayor parte del combustible vertido en el cohete iría al transporte de combustible? En realidad, la fórmula Tsiolkovsky, que une la
M inicial y la masa final del cohete
m con la velocidad
V y la velocidad de escape del motor
u , nos dice lo mismo:
M /
m = e
V / u [2]
A primera vista, no es del todo obvio ¿qué tiene que ver el contenido de energía por kilogramo? Pero todo es simple. Se "sienta" en
usted , a la tasa de vencimiento. Para el combustible químico, está limitado por (y a una primera aproximación igual a)
u = √ (2
q ), donde
q es el calor específico de la combustión. ¿Cuál es el contenido de energía por kilogramo? Y cuando este
q "se queda corto", la relación de masa al inicio y al final resulta ser exponencialmente enorme:
M /
m = e
V / √ (2 q ) [3]
O
V = Ln (
M /
m ) * √ (
2q ) [3a]
Algunas notas, para nerds y para mayor claridad.1. Sí, hay expresiones más precisas para el caudal que
u = √ (
2q ). Cuando les pasé el crédito, Gorbachov "entregó" la URSS. Pero estas fórmulas son complicadas, asustan a los lectores y tienen en cuenta los efectos que no son importantes aquí.
u = √ (
2q ), aunque exagera la respuesta en un 10-30%, describe adecuadamente la dependencia que nos interesa. Y sí, existe un impulso específico, pero en este artículo en particular, la velocidad de flujo es más conveniente de usar.
2. En principio, nada prohíbe incluso un cohete químico para obtener una velocidad de salida
u superior a √ (2
q ). Como? Bueno, digamos, para quemar combustible no en una boquilla, sino en un generador, generando energía eléctrica. Luego, con esta energía, acelere la fracción
x del escape (0 <
x ≤ 1) a velocidades muy altas. Por ejemplo, un motor a reacción eléctrico de plasma
[ 230 ] . Y los residuos de escape se vierten estúpidamente a velocidad cero. Para simplificar, asumimos que todas las transformaciones ocurren sin pérdida de energía, con un 100% de eficiencia. ¿Acelerará tal cohete a una velocidad
V más alta con una relación de masa fija
M /
m (es decir, será más efectivo)?
La respuesta es no. Es fácil resolver las ecuaciones que describen el movimiento de dicho cohete y obtener:
V = Ln (
M /
m ) * √ (
2qx )
Es decir su velocidad final será solo √
x del cohete "ordinario" mecanografiado con combustión directa de combustible (cf. [3a]). Y esta velocidad todavía está rígidamente ligada a
q .
3. ¿Qué pasa si el cohete no funciona con combustible, sino con batería? Bueno, que haya un medio de trabajo separado de masa
m f a bordo y por separado una batería con una reserva de energía
E y masa
m b .
Lo primero que debe comprender aquí es que la batería debe consistir en muchos "módulos" pequeños que se restablecen a medida que funcionan. De lo contrario, llevaremos con nosotros la carga "muerta" de baterías vacías. Pero si es así, entonces conceptualmente no es diferente del combustible ordinario a bordo con una reserva de energía total
E y masa
m f +
m b . Y si
q =
E / (
m f +
m b ) de dicho sistema es más bajo que el de un cohete químico convencional, entonces no volará mejor.
5. Pero, ¿qué pasa con los motores de cohetes eléctricos
[ 225 ] ? Después de todo, dan caudales de decenas y cientos de kilómetros por segundo, y realizaron maniobras interplanetarias exitosas con relaciones
M /
m muy modestas. ¿Cómo es eso? El hecho es que los ERD son sistemas abiertos. Llevan el fluido de trabajo (mercurio, xenón, etc.) con ellos. Pero la energía no lo es. La energía proviene de paneles solares. Si, en cambio, llevaran baterías ordinarias con un contenido energético de masa
q , entonces su eficiencia no sería mayor, según la fórmula [3a].
El artículo fue escrito para el sitio https://habr.com . Al copiar, consulte la fuente. El autor del artículo es Evgeny Bobukh .Por lo tanto, los misiles son caros porque su diseño "seco" extremadamente ligero se ve obligado a soportar una carga extremadamente pesada, principalmente combustible (e incluso "bombearlo" rápidamente a través del TNA). Y la carga es excelente porque nuestro combustible es demasiado pesado. Se coloca muy poco en julios por kilogramo.
Ahora entendamos las razones de esta limitación.
¿Por qué mirar más de cerca la reacción de la combustión de hidrógeno en flúor como una de las más simples? En él, los pares de hidrógeno-hidrógeno y flúor-flúor intercambian parejas, creando dos pares de hidrógeno-flúor:
H 2 +
F 2 = 2
HF¿De dónde viene la energía liberada?
Una molécula de hidrógeno tiene dos átomos. Los átomos tienen electrones. Están "esparcidos" alrededor del átomo en forma de una especie de nube, y están conectados con el núcleo principalmente por atracción electrostática. Los electrones son externos, de valencia y (excepto hidrógeno) internos, no participan en reacciones químicas. Después de la reacción, el hidrógeno y el flúor cambian de lugar. Las nubes eléctricas de electrones de valencia se redistribuyen y cambian ligeramente su forma. Algo como esto:
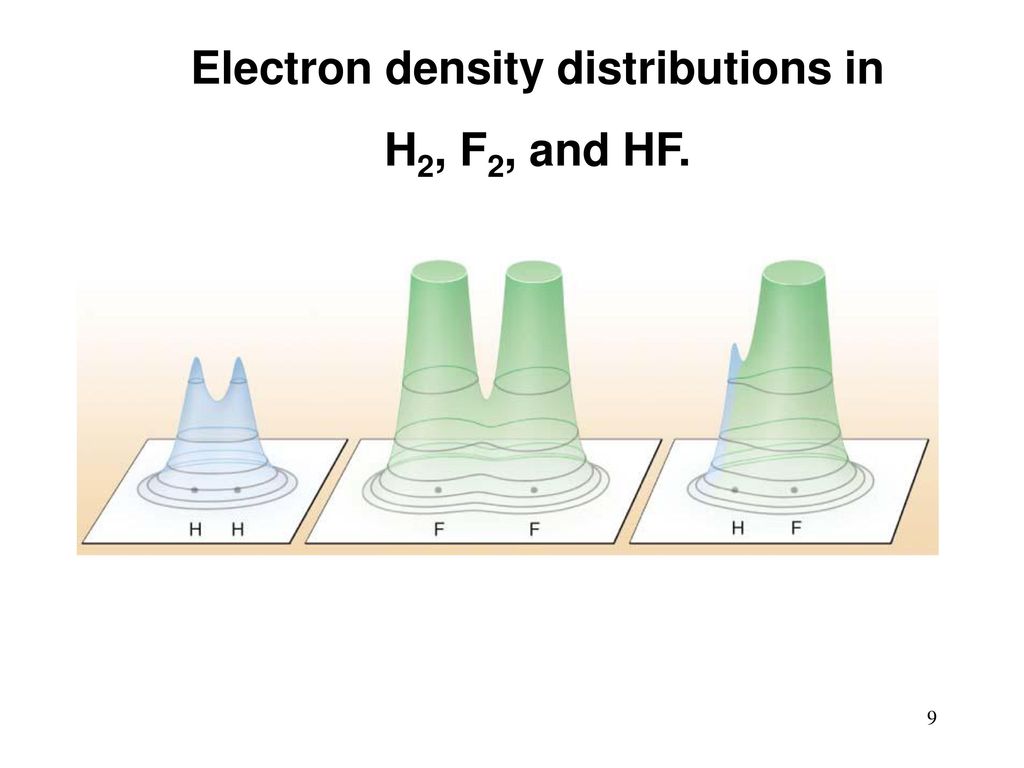
[Crédito de la imagen [
295 ]]
La energía potencial de unión de los electrones con los átomos en las nubes nuevas es diferente. En este caso (esta energía es negativa), ahora es menor que la de
H 2 y
F 2 por separado. ¿A dónde fue la diferencia? La energía cinética de una molécula, las vibraciones de sus átomos, la radiación electromagnética. Todo esto eventualmente se convirtió en calor. Lo que expandió el gas y le dio tracción.
Y aquí está el momento crítico. Solo los electrones de valencia externos están involucrados en las reacciones químicas. La distribución de densidad de otros electrones (así como el campo eléctrico "en la profundidad" del átomo) permanecen prácticamente sin cambios. En las reacciones químicas, los átomos interactúan entre sí como a través de "intermediarios", que son electrones de valencia:
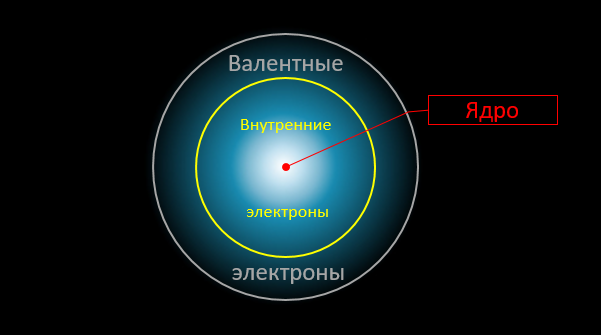
Ahora, atención, la pregunta es: ¿cuál es la energía máxima posible que se puede liberar durante tal "permutación"? Obviamente, no puede exceder la suma de las energías de unión de los electrones externos con los átomos (en el producto final e inicial). Pero estas energías vinculantes son bien conocidas por nosotros
[ 285 ] . Por átomo, ascienden a 1.5 - 25
electronvoltios (
eV ) y se expresan en fracciones de la constante de Rydberg, un valor fundamental construido a partir de las constantes básicas de nuestro Universo:
Ry (en el sistema gaussiano) =
m e e 4/2 ħ 2 =
1 3 .6 eV [
300 ]
Además, tanto 25 como 13.6 eV son inalcanzables. En las reacciones típicas, lejos de toda la energía de unión, se libera, pero solo su diferencia entre las dos configuraciones y, por lo tanto, el techo práctico de la liberación de energía de la química es de 3-4 eV por átomo. En términos de un kilogramo típico de combustible + oxidante, esto equivale a 20-30 MJ de energía liberada. Es esta cantidad la que establece la velocidad de gas máxima teórica de un motor de reacción química con combustión directa
u = √ (2
q ) = √ (2 * 2.5 * 10
7 ) ≈ 7000 m / s. Inasequible, por supuesto, porque no tiene en cuenta las pérdidas en los grados internos de libertad de las moléculas, disociación, radiación, movimiento térmico no direccional, etc.
Puede parecer que los calores tabulares de combustión
[ 240 ] (digamos, 120 MJ / kg para hidrógeno) contradicen la figura escrita anteriormente. Pero el hecho es que estos calores generalmente se indican por kilogramo de
combustible , sin tener en cuenta el oxidante requerido para su combustión. El cohete lleva ambos componentes consigo, y si recalcula la energía liberada por kilogramo de la
mezcla (con combustión equilibrada), emerge una imagen completamente diferente
[ 240 ] [ 250 ] [ 260 ] :
| Combustible + oxidante | Reacción | Valor calorífico por kg. combustible, MJ / kg | 1 kg de combustible necesita un oxidante, kg. | Valor calorífico, MJ / kg | La salida por átomo de la mezcla, eV |
| Hidrógeno + oxígeno | 2H 2 + O 2 = 2H 2 O | 120 | 8 | 13,3 | 0,83 |
| Queroseno + oxígeno | 2C 12 H 26 + 37O 2 = 24CO 2 + 26H 2 O | 43 | 3.5 | 9.6 | 1.02 |
| Carbón + Oxígeno | C + O 2 = CO 2 | 33 | 2.7 | 9.0 | 1,38 |
| Litio + oxígeno | 4Li + O 2 = 2Li 2 O | 43,5 | 1,2 | 20,2 | 2.10 |
| Boro + Oxígeno | 2B + 1.5O 2 = B 2 O 3 | 57,2 | 2.2 2.2 | 17,8 | 2,58 |
| Magnesio + Oxígeno | 2Mg + O 2 = 2MgO | 25,1 | 0.7 | 15,1 | 3.18 |
| Berilio + oxígeno | 2Be + O 2 = 2BeO | 66,6 | 1,8 | 24,0 | 3.12 |
| Litio + flúor | 2Li + F 2 = 2LiF | 88,8 | 2.7 | 23,7 | 3.21 |
| Berilio + Fluoruro | Be + F 2 = BeF 2 | 114 | 4.2 4.2 | 21,9 | 3,57 |
| Dicianoacetileno + ozono | C 4 N 2 + (4/3) O 3 = 4 CO + N 2 | 16,2 | 0.8 | 8.8 | 1,28 |
Como puede ver, incluso los más intensivos en energía, aunque no aptos para un uso práctico, los combustibles producen solo 24 MJ / kg de calor durante la combustión. Y nos hemos topado con este límite casi desde el comienzo de la astronáutica, que muestra un gráfico de la tasa de flujo de salida de los motores químicos según el año de su creación:

[Motores iniciales según [
310 ], [
320 ], [
330 ], más adelante - Wikipedia individualmente. Recolección de datos
aquí ]
Parece que el potencial del combustible químico se ha desarrollado durante mucho tiempo. ¿Es posible comenzar a almacenar energía de una forma diferente?
Continuará