Compresión de datos de Huffman

Entrada

En este artículo hablaré sobre el conocido algoritmo Huffman, así como su aplicación en la compresión de datos.

Como resultado, escribiremos un archivador simple. Ya había un artículo al respecto sobre Habré , pero sin implementación práctica. El material teórico de la publicación actual está tomado de las lecciones de informática de la escuela y del libro de Robert Lafore "Estructuras de datos y algoritmos en Java". Entonces, ¡todo está por debajo!

Un poco de pensamiento

En un archivo de texto plano, un carácter está codificado con 8 bits (codificación ASCII) o 16 (codificación Unicode). Además consideraremos la codificación ASCII. Por ejemplo, tome la línea s1 = "SUSIE DICE QUE ES FÁCIL \ n". En total, hay 22 caracteres en la línea, por supuesto, incluidos los espacios y el carácter de nueva línea - '\ n'. Un archivo que contiene esta línea pesará 22 * ​​8 = 176 bits. La pregunta surge de inmediato: ¿es racional usar los 8 bits para codificar 1 carácter? No utilizamos todos los caracteres ASCII. Incluso si se usa, sería más racional que la letra más frecuente, S, diera el código más corto posible, y que la letra más rara, T (o U, o '\ n'), diera un código más auténtico. Este es el algoritmo de Huffman: necesita encontrar la mejor opción de codificación, en la que el archivo tendrá un peso mínimo. Es bastante normal que las longitudes de los códigos difieran para los diferentes caracteres; esta es la base del algoritmo.

Codificación

¿Por qué no le da al carácter 'S' un código, por ejemplo, 1 bit de longitud: 0 o 1. Déjelo ser 1. Luego le daremos el segundo carácter más encontrado - '' (espacio) - 0. Imagínese, usted comenzó a decodificar su mensaje - cadena codificada s1, y ve que el código comienza con 1. Entonces, ¿qué hacer? ¿Es un carácter S, o es algún otro carácter, por ejemplo A? Por lo tanto, surge una regla importante:

Ningún código debe ser un prefijo de otro

Esta regla es la clave en el algoritmo. Por lo tanto, la creación del código comienza con la tabla de frecuencias, que indica la frecuencia (número de ocurrencias) de cada carácter:

Los caracteres con más ocurrencias deben codificarse con el menor número posible de bits. Daré un ejemplo de una de las posibles tablas de códigos:

Por lo tanto, el mensaje codificado se verá así:

10 01111 10 110 1111 00 10 010 1110 10 00 110 0110 00 110 10 00 1111 010 10 1110 01110 

Separé el código de cada personaje con un espacio. ¡Esto realmente no sucederá en un archivo comprimido!
Surge la pregunta: ¿cómo surgió esta salaga con un código ? ¿Cómo crear una tabla de códigos? Esto se discutirá a continuación.

Construyendo un árbol huffman

Aquí los árboles de búsqueda binarios vienen al rescate. No se preocupe, aquí no se requieren los métodos de búsqueda, inserción y eliminación. Aquí está la estructura de árbol en Java:

 public class Node { private int frequence; private char letter; private Node leftChild; private Node rightChild; ... } 

 class BinaryTree { private Node root; public BinaryTree() { root = new Node(); } public BinaryTree(Node root) { this.root = root; } ... } 

Este no es un código completo, el código completo estará debajo.

Aquí está el algoritmo de construcción del árbol en sí:

1. Cree un objeto Nodo para cada carácter del mensaje (línea s1). En nuestro caso, habrá 9 nodos (objetos de nodo). Cada nodo consta de dos campos de datos: símbolo y frecuencia.
2. Cree un objeto Tree (BinaryTree) para cada uno de los nodos Node. El nodo se convierte en la raíz del árbol.
3. Pegue estos árboles en la cola de prioridad. Cuanto menor es la frecuencia, mayor es la prioridad. Por lo tanto, al extraer, el dervo siempre se selecciona con la frecuencia más baja.

A continuación, debe hacer lo siguiente cíclicamente:

1. Extraiga dos árboles de la cola de prioridad y conviértalos en descendientes del nuevo nodo (el nodo recién creado sin una letra). La frecuencia del nuevo nodo es igual a la suma de las frecuencias de dos árboles descendientes.
2. Para este nodo, cree un árbol con una raíz en este nodo. Pegue este árbol nuevamente en la cola de prioridad. (Dado que el árbol tiene una nueva frecuencia, lo más probable es que llegue a un nuevo lugar en la cola)
3. Continúe los pasos 1 y 2 hasta que solo quede un árbol en la cola: el árbol Huffman

Considere este algoritmo en la línea s1:



Aquí, el símbolo "lf" (salto de línea) indica la transición a una nueva línea, "sp" (espacio) es un espacio.

Que sigue

Tenemos un árbol Huffman. Bien ¿Y qué hacer con eso? No lo tomarán gratis. Y luego, debes rastrear todos los caminos posibles desde la raíz hasta las hojas del árbol. Aceptemos designar el borde 0 si conduce al descendiente izquierdo y 1 si al derecho. Estrictamente hablando, en estas anotaciones, el código del símbolo es la ruta desde la raíz del árbol hasta la hoja que contiene este mismo símbolo.



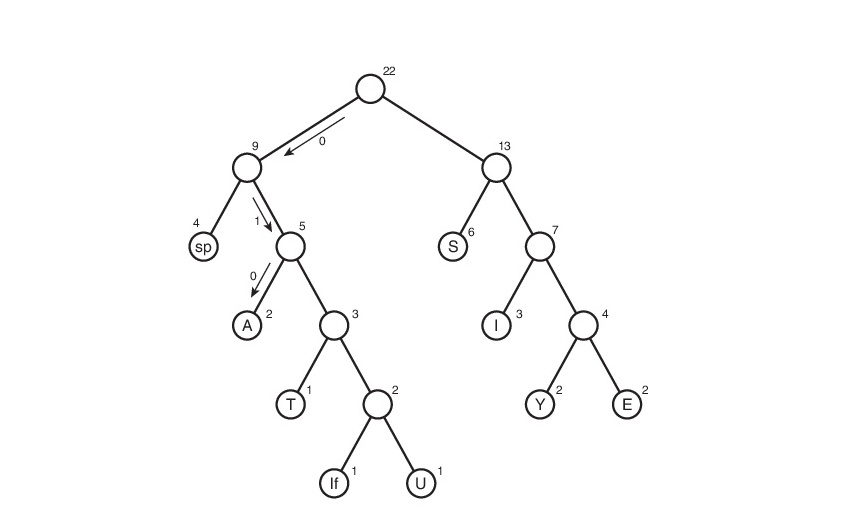
Así, la tabla de códigos resultó. Tenga en cuenta que si consideramos esta tabla, podemos concluir sobre el "peso" de cada carácter: esta es la longitud de su código. Entonces el archivo comprimido pesará: 2 * 3 + 2 * 4 + 3 * 3 + 6 * 2 + 1 * 4 + 1 * 5 + 2 * 4 + 4 * 2 + 1 * 5 = 65 bits. Inicialmente, pesaba 176 bits. ¡Por lo tanto, lo redujimos hasta 176/65 = 2.7 veces! Pero esto es utopía. Es poco probable que se obtenga dicho coeficiente. Por qué Esto se discutirá un poco más tarde.

Decodificación

Bueno, quizás lo más simple que queda es la decodificación. Creo que muchos de ustedes adivinaron que es imposible crear simplemente un archivo comprimido sin ningún indicio de cómo se codificó; ¡no podremos decodificarlo! Sí, fue difícil para mí darme cuenta de esto, pero tuve que crear un archivo de texto table.txt con una tabla de compresión:

 01110 00 A010 E1111 I110 S10 T0110 U01111 Y1110 

Registre la tabla en forma de "carácter" "código de carácter". ¿Por qué es 01110 sin un personaje? De hecho, es con un carácter, solo las herramientas de Java que utilizo cuando imprimo en un archivo, el carácter de nueva línea es '\ n' -convertir a una nueva línea (no importa cuán estúpido suene). Por lo tanto, la línea vacía en la parte superior es el carácter para el código 01110. Para el código 00, el carácter es un espacio al comienzo de la línea. Debo decir de inmediato que nuestro método para almacenar esta tabla puede ser el más irracional. Pero es simple de entender e implementar. Estaré encantado de escuchar sus recomendaciones en los comentarios sobre la optimización.

Tener esta mesa es muy fácil de decodificar. Recuerde qué regla nos guió al crear la codificación:

Ningún código debe anteponer otro

Aquí es donde juega un papel facilitador. Leemos secuencialmente bit a bit y, tan pronto como la cadena d recibida, que consiste en bits de lectura, coincide con la codificación correspondiente al carácter del carácter, inmediatamente sabemos que el carácter del carácter fue codificado (¡y solo eso!). A continuación, escribimos caracteres en la línea de decodificación (la línea que contiene el mensaje decodificado), ponemos a cero la línea d y luego leemos el archivo codificado.

Implementación

Es hora de humillar mi código escribiendo un archivador. Llamémoslo compresor.

Comencemos desde el principio. Primero, escribimos la clase Node:

 public class Node { private int frequence;// private char letter;// private Node leftChild;//  private Node rightChild;//  public Node(char letter, int frequence) { //,  this.letter = letter; this.frequence = frequence; } public Node() {}//    (.       ) public void addChild(Node newNode) {//  if (leftChild == null)//  =>  =>    leftChild = newNode; else { if (leftChild.getFrequence() <= newNode.getFrequence()) // ,   rightChild = newNode;// ,     else { rightChild = leftChild; leftChild = newNode; } } frequence += newNode.getFrequence();//  } public Node getLeftChild() { return leftChild; } public Node getRightChild() { return rightChild; } public int getFrequence() { return frequence; } public char getLetter() { return letter; } public boolean isLeaf() {//   return leftChild == null && rightChild == null; } } 

Ahora el arbol:

 class BinaryTree { private Node root; public BinaryTree() { root = new Node(); } public BinaryTree(Node root) { this.root = root; } public int getFrequence() { return root.getFrequence(); } public Node getRoot() { return root; } } 

Cola prioritaria:

 import java.util.ArrayList;//-,      class PriorityQueue { private ArrayList<BinaryTree> data;//  private int nElems;//-    public PriorityQueue() { data = new ArrayList<BinaryTree>(); nElems = 0; } public void insert(BinaryTree newTree) {// if (nElems == 0) data.add(newTree); else { for (int i = 0; i < nElems; i++) { if (data.get(i).getFrequence() > newTree.getFrequence()) {//     data.add(i, newTree);// . ,  c       1  break;//       } if (i == nElems - 1) data.add(newTree); } } nElems++;// -   1 } public BinaryTree remove() {//   BinaryTree tmp = data.get(0);//   data.remove(0);//,  nElems--;// -   1 return tmp;//  (   ) } } 

La clase que crea el árbol Huffman:

 public class HuffmanTree { private final byte ENCODING_TABLE_SIZE = 127;//   private String myString;// private BinaryTree huffmanTree;//  private int[] freqArray;//  private String[] encodingArray;//  //----------------constructor---------------------- public HuffmanTree(String newString) { myString = newString; freqArray = new int[ENCODING_TABLE_SIZE]; fillFrequenceArray(); huffmanTree = getHuffmanTree(); encodingArray = new String[ENCODING_TABLE_SIZE]; fillEncodingArray(huffmanTree.getRoot(), "", ""); } //--------------------frequence array------------------------ private void fillFrequenceArray() { for (int i = 0; i < myString.length(); i++) { freqArray[(int)myString.charAt(i)]++; } } public int[] getFrequenceArray() { return freqArray; } //------------------------huffman tree creation------------------ private BinaryTree getHuffmanTree() { PriorityQueue pq = new PriorityQueue(); //   for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { if (freqArray[i] != 0) {//     Node newNode = new Node((char) i, freqArray[i]);//    Node BinaryTree newTree = new BinaryTree(newNode);//  Node  BinaryTree pq.insert(newTree);//   } } while (true) { BinaryTree tree1 = pq.remove();//    . try { BinaryTree tree2 = pq.remove();//     Node newNode = new Node();//  Node newNode.addChild(tree1.getRoot());//      newNode.addChild(tree2.getRoot()); pq.insert(new BinaryTree(newNode); } catch (IndexOutOfBoundsException e) {//     return tree1; } } } public BinaryTree getTree() { return huffmanTree; } //-------------------encoding array------------------ void fillEncodingArray(Node node, String codeBefore, String direction) {//   if (node.isLeaf()) { encodingArray[(int)node.getLetter()] = codeBefore + direction; } else { fillEncodingArray(node.getLeftChild(), codeBefore + direction, "0"); fillEncodingArray(node.getRightChild(), codeBefore + direction, "1"); } } String[] getEncodingArray() { return encodingArray; } public void displayEncodingArray() {//  fillEncodingArray(huffmanTree.getRoot(), "", ""); System.out.println("======================Encoding table===================="); for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { if (freqArray[i] != 0) { System.out.print((char)i + " "); System.out.println(encodingArray[i]); } } System.out.println("========================================================"); } //----------------------------------------------------- String getOriginalString() { return myString; } } 

Clase que contiene qué codifica / decodifica:

 public class HuffmanOperator { private final byte ENCODING_TABLE_SIZE = 127;//  private HuffmanTree mainHuffmanTree;//  (   ) private String myString;//  private int[] freqArray;//  private String[] encodingArray;//  private double ratio;//  public HuffmanOperator(HuffmanTree MainHuffmanTree) {//for compress this.mainHuffmanTree = MainHuffmanTree; myString = mainHuffmanTree.getOriginalString(); encodingArray = mainHuffmanTree.getEncodingArray(); freqArray = mainHuffmanTree.getFrequenceArray(); } public HuffmanOperator() {}//for extract; //---------------------------------------compression----------------------------------------------------------- private String getCompressedString() { String compressed = ""; String intermidiate = "";// (  ) //System.out.println("=============================Compression======================="); //displayEncodingArray(); for (int i = 0; i < myString.length(); i++) { intermidiate += encodingArray[myString.charAt(i)]; } //      .       8=> //    ( 1,  ) byte counter = 0;//     (   : 0<=counter<8<127) for (int length = intermidiate.length(), delta = 8 - length % 8; counter < delta ; counter++) {//delta -    intermidiate += "0"; } // -         compressed = String.format("%8s", Integer.toBinaryString(counter & 0xff)).replace(" ", "0") + intermidiate; //  setCompressionRatio(); //System.out.println("==============================================================="); return compressed; } private void setCompressionRatio() {//   double sumA = 0, sumB = 0;//A-the original sum for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { if (freqArray[i] != 0) { sumA += 8 * freqArray[i]; sumB += encodingArray[i].length() * freqArray[i]; } } ratio = sumA / sumB; } public byte[] getBytedMsg() {//final compression StringBuilder compressedString = new StringBuilder(getCompressedString()); byte[] compressedBytes = new byte[compressedString.length() / 8]; for (int i = 0; i < compressedBytes.length; i++) { compressedBytes[i] = (byte) Integer.parseInt(compressedString.substring(i * 8, (i + 1) * 8), 2); } return compressedBytes; } //---------------------------------------end of compression---------------------------------------------------------------- //------------------------------------------------------------extract----------------------------------------------------- public String extract(String compressed, String[] newEncodingArray) { String decompressed = ""; String current = ""; String delta = ""; encodingArray = newEncodingArray; //displayEncodingArray(); // -   for (int i = 0; i < 8; i++) delta += compressed.charAt(i); int ADDED_ZEROES = Integer.parseInt(delta, 2); for (int i = 8, l = compressed.length() - ADDED_ZEROES; i < l; i++) { //i = 8, ..      -   current += compressed.charAt(i); for (int j = 0; j < ENCODING_TABLE_SIZE; j++) { if (current.equals(encodingArray[j])) {//  decompressed += (char)j;//   current = "";//    } } } return decompressed; } public String getEncodingTable() { String enc = ""; for (int i = 0; i < encodingArray.length; i++) { if (freqArray[i] != 0) enc += (char)i + encodingArray[i] + '\n'; } return enc; } public double getCompressionRatio() { return ratio; } public void displayEncodingArray() {//  System.out.println("======================Encoding table===================="); for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { //if (freqArray[i] != 0) { System.out.print((char)i + " "); System.out.println(encodingArray[i]); //} } System.out.println("========================================================"); } } 

Clase que facilita la escritura en un archivo:

 import java.io.File; import java.io.PrintWriter; import java.io.FileNotFoundException; import java.io.FileOutputStream; import java.io.IOException; import java.io.Closeable; public class FileOutputHelper implements Closeable { private File outputFile; private FileOutputStream fileOutputStream; public FileOutputHelper(File file) throws FileNotFoundException { outputFile = file; fileOutputStream = new FileOutputStream(outputFile); } public void writeByte(byte msg) throws IOException { fileOutputStream.write(msg); } public void writeBytes(byte[] msg) throws IOException { fileOutputStream.write(msg); } public void writeString(String msg) { try (PrintWriter pw = new PrintWriter(outputFile)) { pw.write(msg); } catch (FileNotFoundException e) { System.out.println(" ,     !"); } } @Override public void close() throws IOException { fileOutputStream.close(); } public void finalize() throws IOException { close(); } } 

Clase que facilita la lectura de un archivo:

 import java.io.FileInputStream; import java.io.EOFException; import java.io.BufferedReader; import java.io.InputStreamReader; import java.io.Closeable; import java.io.File; import java.io.IOException; public class FileInputHelper implements Closeable { private FileInputStream fileInputStream; private BufferedReader fileBufferedReader; public FileInputHelper(File file) throws IOException { fileInputStream = new FileInputStream(file); fileBufferedReader = new BufferedReader(new InputStreamReader(fileInputStream)); } public byte readByte() throws IOException { int cur = fileInputStream.read(); if (cur == -1)//   throw new EOFException(); return (byte)cur; } public String readLine() throws IOException { return fileBufferedReader.readLine(); } @Override public void close() throws IOException{ fileInputStream.close(); } } 

Bueno, y la clase principal:

 import java.io.File; import java.nio.charset.MalformedInputException; import java.io.FileNotFoundException; import java.io.IOException; import java.nio.file.Files; import java.nio.file.NoSuchFileException; import java.nio.file.Paths; import java.util.List; import java.io.EOFException; public class Main { private static final byte ENCODING_TABLE_SIZE = 127; public static void main(String[] args) throws IOException { try {//       if (args[0].equals("--compress") || args[0].equals("-c")) compress(args[1]); else if ((args[0].equals("--extract") || args[0].equals("-x")) && (args[2].equals("--table") || args[2].equals("-t"))) { extract(args[1], args[3]); } else throw new IllegalArgumentException(); } catch (ArrayIndexOutOfBoundsException | IllegalArgumentException e) { System.out.println("    "); System.out.println(" Readme.txt"); e.printStackTrace(); } } public static void compress(String stringPath) throws IOException { List<String> stringList; File inputFile = new File(stringPath); String s = ""; File compressedFile, table; try { stringList = Files.readAllLines(Paths.get(inputFile.getAbsolutePath())); } catch (NoSuchFileException e) { System.out.println(" ,     !"); return; } catch (MalformedInputException e) { System.out.println("    "); return; } for (String item : stringList) { s += item; s += '\n'; } HuffmanOperator operator = new HuffmanOperator(new HuffmanTree(s)); compressedFile = new File(inputFile.getAbsolutePath() + ".cpr"); compressedFile.createNewFile(); try (FileOutputHelper fo = new FileOutputHelper(compressedFile)) { fo.writeBytes(operator.getBytedMsg()); } //create file with encoding table: table = new File(inputFile.getAbsolutePath() + ".table.txt"); table.createNewFile(); try (FileOutputHelper fo = new FileOutputHelper(table)) { fo.writeString(operator.getEncodingTable()); } System.out.println("   : " + compressedFile.getAbsolutePath()); System.out.println("    " + table.getAbsolutePath()); System.out.println("     !"); double idealRatio = Math.round(operator.getCompressionRatio() * 100) / (double) 100;//  double realRatio = Math.round((double) inputFile.length() / ((double) compressedFile.length() + (double) table.length()) * 100) / (double)100;//  System.out.println("    " + idealRatio); System.out.println("      " + realRatio); } public static void extract(String filePath, String tablePath) throws FileNotFoundException, IOException { HuffmanOperator operator = new HuffmanOperator(); File compressedFile = new File(filePath), tableFile = new File(tablePath), extractedFile = new File(filePath + ".xtr"); String compressed = ""; String[] encodingArray = new String[ENCODING_TABLE_SIZE]; //read compressed file //!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!check here: try (FileInputHelper fi = new FileInputHelper(compressedFile)) { byte b; while (true) { b = fi.readByte();//method returns EOFException compressed += String.format("%8s", Integer.toBinaryString(b & 0xff)).replace(" ", "0"); } } catch (EOFException e) { } //-------------------- //read encoding table: try (FileInputHelper fi = new FileInputHelper(tableFile)) { fi.readLine();//skip first empty string encodingArray[(byte)'\n'] = fi.readLine();//read code for '\n' while (true) { String s = fi.readLine(); if (s == null) throw new EOFException(); encodingArray[(byte)s.charAt(0)] = s.substring(1, s.length()); } } catch (EOFException ignore) {} extractedFile.createNewFile(); //extract: try (FileOutputHelper fo = new FileOutputHelper(extractedFile)) { fo.writeString(operator.extract(compressed, encodingArray)); } System.out.println("    " + extractedFile.getAbsolutePath()); } } 

El archivo de instrucciones readme.txt depende de usted para escribir usted mismo :-)

Conclusión

Esto es probablemente todo lo que quería decir. Si tiene algo que decir sobre mi incompetencia de las mejoras en el código, el algoritmo y cualquier optimización en general, no dude en escribir. Si entendí mal algo, también escriba. Estaré encantado de saber de usted en los comentarios!

PS

Sí, sí, todavía estoy aquí, porque no me olvidé del coeficiente. Para la cadena s1, la tabla de codificación pesa 48 bytes, mucho más que el archivo original, y no se olvidaron de ceros adicionales (el número de ceros agregados es 7) => la relación de compresión será menor que uno: 176 / (65 + 48 * 8 + 7) = 0.38. Si también te diste cuenta de esto, simplemente no estás bien hecho. Sí, esta implementación será extremadamente ineficiente para archivos pequeños. Pero, ¿qué pasa con los archivos grandes? Los tamaños de archivo superan con creces el tamaño de la tabla de codificación. ¡Aquí el algoritmo funciona como debería! Por ejemplo, para el monólogo de Fausto, el archivador proporciona un coeficiente real (no idealizado) igual a 1,46, ¡casi una vez y media! Y sí, se suponía que el archivo estaba en inglés.