Escribir XGBoost desde cero - parte 1: árboles de decisión

Hola Habr!

Después de numerosas búsquedas de guías de alta calidad sobre árboles de decisión y algoritmos de conjunto (impulso, bosque de decisión, etc.) con su implementación directa en lenguajes de programación, y sin encontrar nada (quien encuentre, escriba en los comentarios, tal vez aprenderé algo nuevo), Decidí hacer mi propio liderazgo, como me gustaría verlo. La tarea en palabras es simple, pero, como saben, el demonio está en las pequeñas cosas, de las cuales hay muchos algoritmos con árboles.

Dado que el tema es bastante extenso, será muy difícil incluir todo en un artículo, por lo que habrá dos publicaciones: la primera está dedicada a los árboles y la segunda parte estará dedicada a la implementación del algoritmo de aumento de gradiente. Todo el material presentado aquí está compilado y diseñado en base a fuentes abiertas, mi código, el código de colegas y amigos. Te advierto de inmediato, habrá mucho código.



Entonces, ¿qué necesita saber y poder aprender a escribir sus propios algoritmos de conjunto con árboles de decisión desde cero? Dado que un conjunto de algoritmos no es más que una composición de "algoritmos débiles", escribir un buen conjunto requiere buenos "algoritmos débiles", los analizaremos en detalle en este artículo. Como su nombre lo indica, estos son árboles cruciales, y pasando de lo simple a lo complejo, aprenderemos cómo escribirlos. En este caso, el énfasis se pondrá directamente en la implementación, toda la teoría se presentará en un mínimo, básicamente daré enlaces a materiales para estudio independiente.

Para aprender el material, debe comprender cuán bueno o malo es nuestro algoritmo. Lo entenderemos de manera muy simple: arreglaremos algunos conjuntos de datos específicos y compararemos nuestros algoritmos con los algoritmos de árboles de Sklearn (bueno, lo que sucedería sin esta biblioteca). Compararemos mucho: la complejidad del algoritmo, las métricas de datos, el tiempo de actividad, etc.

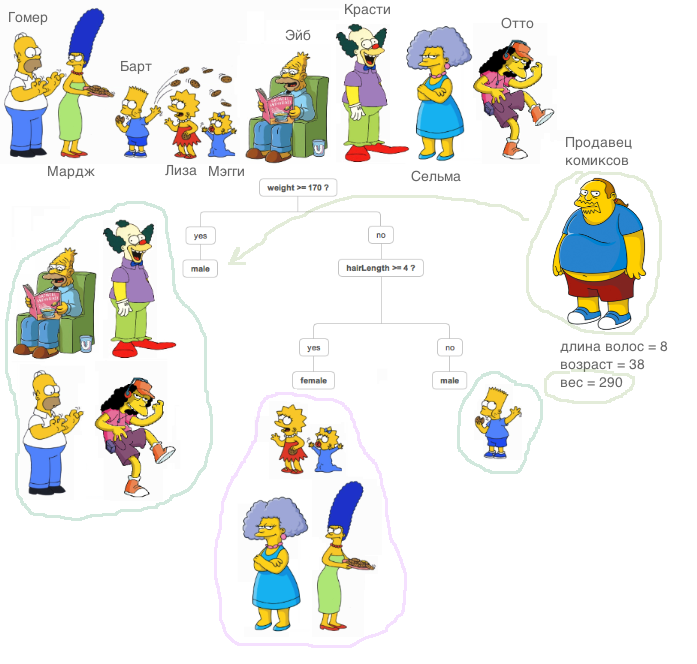
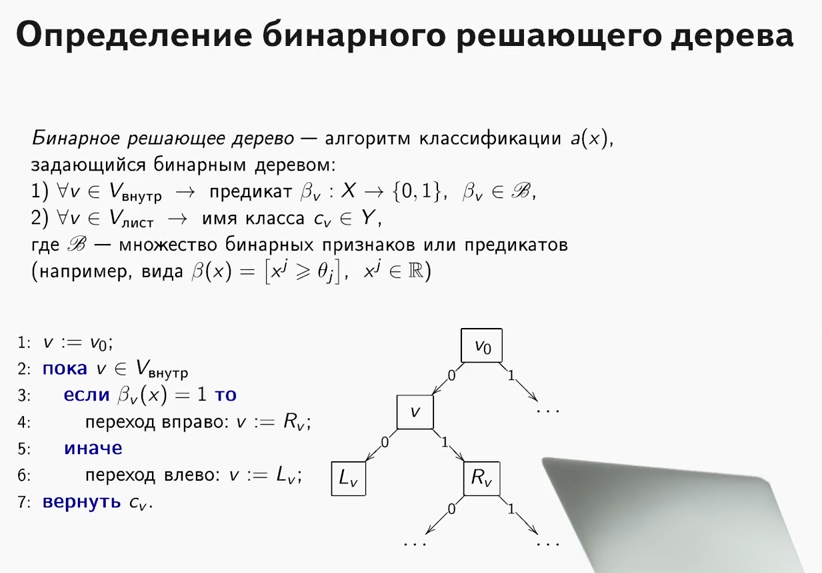
¿Qué es un árbol decisivo? Un material muy bueno, que explica el principio del árbol de decisiones, está contenido en el curso de SAO (por cierto, un curso genial, lo recomiendo a aquellos que comienzan a conocer ML).

Una explicación muy importante: en todos los casos descritos a continuación, todos los signos serán reales, no haremos transformaciones especiales con datos fuera de los algoritmos (comparamos algoritmos, no conjuntos de datos).

Ahora aprendamos cómo resolver el problema de la regresión usando árboles de decisión. Utilizaremos la métrica MSE como entropía.

Implementamos una clase RegressionTree muy simple, que se basa en un enfoque recursivo. Intencionalmente, comenzamos con una implementación muy ineficaz, pero fácil de entender, de tal clase para poder mejorarla en el futuro.

1. Clase RegressionTree ()

 class RegressionTree(): '''  RegressionTree   .    ,      . ''' def __init__(self, max_depth=3, n_epoch=10, min_size=8): '''   . ''' self.max_depth = max_depth #   self.min_size = min_size #    self.value = 0 #    (   ) self.feature_idx = -1 #    self.feature_threshold = 0 #    self.left = None #   self.right = None #   def fit(self, X, y): '''   .     . ''' #    self.value = y.mean() base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #       prev_error_left = base_error prev_error_right = 0 #     0 -  if self.max_depth <= 1: return dim_shape = X.shape[1] #       left_value = 0 right_value = 0 #     for feat in range(dim_shape): #   idxs = np.argsort(X[:, feat]) #        N = X.shape[0] N1, N2 = N, 0 thres = 1 #      while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #    if thres < N - 1 and x == X[idxs[thres + 1], feat]: thres += 1 continue # ,         target_right = y[idxs][:thres] target_left = y[idxs][thres:] mean_right = y[idxs][:thres].mean(), mean_left = y[idxs][thres:].mean() #        - #   (  ) left_shape = target_left.shape[0] right_shape = target_right.shape[0] mean_left_array = [mean_left for _ in range(left_shape)] mean_right_array = [mean_right for _ in range(right_shape)] #      prev_error_left = N1/N * mse(target_left, mean_left_array) prev_error_right = N2/N * mse(target_right, mean_right_array) #    ,   if (prev_error_left + prev_error_right < error): if (min(N1,N2) > self.min_size): self.feature_idx = feat self.feature_threshold = x left_value = mean_left right_value = mean_right flag = 1 error = prev_error_left + prev_error_right thres += 1 #     ,  if self.feature_idx == -1: return #   -   ,    #   -     self.left = RegressionTree(self.max_depth - 1) self.left.value = left_value self.right = RegressionTree(self.max_depth - 1) self.right.value = right_value #   idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #  self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, x): '''     -  ,         self.value -    . ''' if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, X): '''    -      __predict(). ''' y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

Explicaré brevemente qué hace cada método aquí.

El método de fit , como su nombre lo indica, enseña el modelo. Se aplica una muestra de capacitación a la entrada y se lleva a cabo un procedimiento de capacitación en árbol. Al ordenar los signos, estamos buscando la mejor partición del árbol en términos de reducción de la entropía, en este caso mse . Para determinar que fue posible encontrar una buena división es muy simple, es suficiente para cumplir dos condiciones. No queremos que caigan pocos objetos en la partición (protección contra reentrenamiento), y el error promedio para mse debería ser menor que el error que está ahora en el árbol: estamos buscando la misma ganancia en ganancia de información . Después de pasar por todos los signos y todos los valores únicos de tal manera, revisaremos todas las opciones y elegiremos la mejor partición. Y luego hacemos una llamada recursiva en las particiones recibidas hasta que se cumplan las condiciones para salir de la recursividad.

El método __predict , como su nombre lo indica, hace un predicado. Habiendo recibido un objeto como entrada, pasa a través de los nodos del árbol resultante: en cada nodo, el número y el valor del atributo están fijos en él, y dependiendo del valor que utilice el método entrante del objeto para este atributo, vamos hacia el descendiente derecho o hacia la izquierda, hasta llegar a la hoja, en la que habrá una respuesta para este objeto.

El método de predict hace lo mismo que el método anterior, solo para un grupo de objetos.

Importamos el conocido conjunto de datos de viviendas de California. Este es un conjunto de datos regular con datos y un objetivo para resolver el problema de regresión.

 data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) 

Bueno, ¡comencemos la comparación! Primero, veamos qué tan rápido aprende el algoritmo. Establecemos en Sklearn y en nosotros el único parámetro max_depth , que sea igual a 2.

 %%time A = RegressionTree(2) #    A.fit(X,y) 

 from sklearn.tree import DecisionTreeRegressor %%time model = DecisionTreeRegressor(max_depth=2) #  Sklearn model.fit(X,y) 

Se mostrará lo siguiente:

• Para nuestro algoritmo: tiempos de CPU: usuario 4min 47s, sys: 8.25 ms, total: 4min 47s
  Tiempo de pared: 4min 47s
• Para Sklearn: tiempos de CPU: usuario 53.5 ms, sys: 0 ns, total: 53.5 ms
  Tiempo de pared: 53.4 ms

Como puede ver, el algoritmo aprende miles de veces más lento. Cual es la razon Vamos a hacerlo bien.

Recuerde cómo se organiza el procedimiento para encontrar la mejor partición. Como saben, en el caso general, con el tamaño de los objetos. $$$N$ y con la cantidad de signos $$$d$ , la dificultad de encontrar la mejor división es $$$O (N * logN * d)$ .

¿De dónde viene esta complejidad?

En primer lugar, para volver a calcular el error de manera efectiva, es necesario ordenar todas las columnas para pasar del más pequeño al más grande antes de pasar por el atributo. A medida que hacemos esto para cada rasgo, esto crea una complejidad correspondiente. Como puede ver, clasificamos los signos, pero el problema radica en volver a calcular el error: cada vez que introducimos los datos en el método mse , que funciona para la línea. ¡Esto hace que el recuento de errores sea tan ineficiente! Después de todo, la dificultad de encontrar una división aumenta a $$$O (N ^ 2 * d)$ para grandes $$$N$ ralentiza enormemente el algoritmo. Por lo tanto, procedemos sin problemas al siguiente elemento.

2. Clase RegressionTree () con recuento rápido de errores

¿Qué se debe hacer para contar rápidamente el error? Tome un bolígrafo y papel y pinte cómo debemos cambiar las fórmulas.

Supongamos que en algún paso ya hay un error calculado para $$$N$ objetos Tiene la siguiente fórmula: $$$\ sum_ {i = 1} ^ n (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2$ . Aquí es necesario dividir por $$$N$ pero por ahora vamos a omitirlo. Queremos obtener este error rápidamente. $$$\ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2$ , es decir, arrojar el error que introduce el elemento $$$y_i$ a otra parte

Como lanzamos el objeto, el error debe relatarse en dos lugares: en el lado derecho (excluyendo este objeto) y en el lado izquierdo (teniendo en cuenta este objeto). Pero sin pérdida de generalidad deduciremos solo una fórmula, ya que serán similares.

Como trabajamos con mse , no tuvimos suerte: es bastante difícil obtener un recuento rápido de un error, pero cuando se trabaja con otras métricas (por ejemplo, el criterio de Gini, si resolvemos el problema de clasificación), el recuento rápido es mucho más fácil.

Bueno, ¡comencemos a derivar fórmulas!

$$

$$\ sum_ {i = 1} ^ N (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2 + (y_N - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2$$

Escribiremos al primer miembro:

$$

$$\ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1 } (y_i - \ frac {\ sum_ {i = 1} ^ {N-1} y_i + y_N} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ frac { Ny_i - \ sum_ {i = 1} ^ {N-1} y_i} {N} - \ frac {y_N} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N} - \ frac {y_N - y_i} {N}) ^ 2 = \\ \ sum_ {i = 1 } ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) ^ 2 - 2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} + (\ frac {y_N - y_i} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) ^ 2 - \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} - (\ frac {y_N - y_i} {N}) ^ 2) = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2 * (\ frac {N-1} {N}) ^ 2 - \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} - \\ - (\ frac {y_N - y_i} { N}) ^ 2)$$

Ugh, solo queda un poco. Solo queda expresar la cantidad requerida.

$$

$$\ sum_ {i = 1} ^ {N} (y_i - \ frac {\ sum_ {i = 1} ^ {N} y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1 } (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2 * (\ frac {N-1} {N}) ^ 2 - \\ \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) (\ frac {y_N - y_i} {N}) - (\ frac {y_N - y_i} {N}) ^ 2) + (y_N - \ sum_ {i = 1} ^ {N} \ frac {y_i} {N}) ^ 2$$

Y luego está claro cómo expresar la cantidad deseada. Para volver a calcular el error, necesitamos almacenar solo la suma de los elementos a la derecha e izquierda, así como el nuevo elemento en sí, que llegó a la entrada. Ahora se cuenta el error para $$$O (1)$ .

Bueno, implementemos esto en el código.

 class RegressionTreeFastMse(): '''  RegressionTree    .        O(1). ''' #    def __init__(self, max_depth=3, min_size=10): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None #   -     def fit(self, X, y): #   -   y self.value = y.mean() #   - mse     (  # ,     )   base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -        delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue # 2 ,    -   #   - -    if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 #   ,  if self.feature_idx == -1: return self.left = RegressionTreeFastMse(self.max_depth - 1) # print ("    %d"%(self.max_depth - 1)) self.left.value = left_value self.right = RegressionTreeFastMse(self.max_depth - 1) # print ("    %d"%(self.max_depth - 1)) self.right.value = right_value idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

Midamos el tiempo que ahora se dedica al entrenamiento y comparemos con el análogo de Sklearn.

 %%time A = RegressionTreeFastMse(4, min_size=5) A.fit(X,y) test_mytree = A.predict(X) test_mytree 

 %%time model = DecisionTreeRegressor(max_depth=4) model.fit(X,y) test_sklearn = model.predict(X) 

• Para nuestro algoritmo, obtenemos - tiempos de CPU: usuario 3.11 s, sys: 2.7 ms, total: 3.11 s
  Tiempo de pared: 3.11 s.
• Para el algoritmo de Sklearn: tiempos de CPU: usuario 45,9 ms, sys: 1,09 ms, total: 47 ms
  Tiempo de pared: 45,7 ms.

Los resultados ya son más agradables. Bueno, sigamos mejorando el algoritmo.

3. Clase RegressionTree () con combinaciones lineales de características

Ahora, en nuestro algoritmo, las relaciones entre los atributos no se utilizan de ninguna manera. Arreglamos una característica y miramos solo las particiones ortogonales del espacio. ¿Cómo aprender a usar las relaciones lineales entre los atributos? Es decir, buscar las mejores particiones no es como $$$a_ {feat} <x$ y $$$\ sum_ {i = 1} ^ K b_i * a_i <x$ donde $$$K$ ¿Es algún número menor que la dimensión de nuestro espacio?

Hay muchas opciones, destacaré dos de las más interesantes desde mi punto de vista. Ambos enfoques se describen en el libro de Friedman (él inventó estos árboles).

Daré una imagen para que quede claro lo que significa:



Primero, puede intentar encontrar estas particiones lineales algorítmicamente. Está claro que es imposible clasificar todas las combinaciones lineales, porque hay un número infinito de combinaciones, por lo que dicho algoritmo debe ser codicioso, es decir, en cada iteración, mejorar el resultado de la iteración anterior. La idea principal de este algoritmo se puede leer en el libro, también dejaré un enlace aquí al repositorio de mi amigo y colega con la implementación de este algoritmo.

En segundo lugar, si no nos alejamos de la idea de encontrar la mejor partición ortogonal, ¿cómo modificamos el conjunto de datos para que se use la información sobre la relación de características y la búsqueda se base en particiones ortogonales? Así es, para hacer algún tipo de transformación de las características originales en otras nuevas. Por ejemplo, puede tomar la suma de alguna combinación de características y buscar particiones por ellas. Tal método encaja peor en el concepto algorítmico, pero realiza su tarea: busca particiones ortogonales que ya están en algún tipo de interconexión de atributos.

Bueno, impleméntelo: agregaremos como nuevas características, por ejemplo, todo tipo de combinaciones de sumas de características $$$i, j$ donde $$$I <j$ . Observo que la complejidad del algoritmo en este caso aumentará, está claro cuántas veces. Bueno, para ser considerado más rápido, usaremos cython.

 %load_ext Cython %%cython -a import itertools import numpy as np cimport numpy as np from itertools import * cdef class RegressionTreeCython: cdef public int max_depth cdef public int feature_idx cdef public int min_size cdef public int averages cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef RegressionTreeCython left cpdef RegressionTreeCython right def __init__(self, max_depth=3, min_size=4, averages=1): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.averages = averages self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None def data_transform(self, np.ndarray[np.float64_t, ndim=2] X, list index_tuples): #   -       for i in index_tuples: #  ,       X = np.hstack((X, X[:, i[0]:(i[1]+1)].sum(axis=1).reshape(X.shape[0],1))) return X def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef np.float64_t mean1 = 0.0 cpdef np.float64_t mean2 = 0.0 cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef np.float64_t delta1 = 0.0 cpdef np.float64_t delta2 = 0.0 cpdef np.float64_t sm1 = 0.0 cpdef np.float64_t sm2 = 0.0 cpdef list index_tuples cpdef list stuff cpdef long idx = 0 cpdef np.float64_t prev_error1 = 0.0 cpdef np.float64_t prev_error2 = 0.0 cpdef long thres = 0 cpdef np.float64_t error = 0.0 cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 #        #  ,     if self.averages: stuff = list(range(0,X.shape[1],1)) index_tuples = list(combinations(stuff,2)) #    X = self.data_transform(X, index_tuples) #   -   y self.value = y.mean() #   - mse     (  , #     )   base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -        delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue # 2    -   #   -      if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 # self.feature_idx -     . #   -  ,    -   #  ,   ,     #   ,  if self.feature_idx == -1: return #    self.left = RegressionTreeCython(self.max_depth - 1, averages=0) self.left.value = left_value self.right = RegressionTreeCython(self.max_depth - 1, averages=0) self.right.value = right_value #      idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #   self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): #   ,        if self.averages: stuff = list(range(0,X.shape[1],1)) index_tuples = list(itertools.combinations(stuff,2)) X = self.data_transform(X, index_tuples) y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

4. Comparación de resultados

Bueno, comparemos los resultados. Compararemos tres algoritmos con los mismos parámetros: un árbol de Sklearn, nuestro árbol ordinario y nuestro árbol con nuevas características. Dividiremos nuestro conjunto de datos en conjuntos de entrenamiento y prueba muchas veces, y calcularemos el error.

 from sklearn.model_selection import KFold def get_metrics(X,y,n_folds=2, model=None): kf = KFold(n_splits=n_folds, shuffle=True) kf.get_n_splits(X) er_list = [] for train_index, test_index in kf.split(X): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] model.fit(X_train,y_train) predict = model.predict(X_test) er_list.append(mse(y_test, predict)) return er_list 

Ahora ejecutemos todos los algoritmos.

 import matplotlib.pyplot as plt data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) er_sklearn_tree = get_metrics(X,y,30,DecisionTreeRegressor(max_depth=4, min_samples_leaf=10)) er_fast_mse_tree = get_metrics(X,y,30,RegressionTreeFastMse(4, min_size=10)) er_averages_tree = get_metrics(X,y,30,RegressionTreeCython(4, min_size=10)) %matplotlib inline data = [er_sklearn_tree, er_fast_mse_tree, er_averages_tree] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['Sklearn Tree', 'Fast Mse Tree', 'Averages Tree']) plt.grid() plt.show() 

Resultados:



Nuestro árbol normal perdió ante Sklearn (lo cual es comprensible: Sklearn está bien optimizado y, de forma predeterminada, utiliza muchos parámetros en el árbol que no tenemos en cuenta), pero al agregar cantidades, el resultado se vuelve más agradable.

Para resumir: aprendimos a escribir árboles decisivos desde cero, aprendimos a mejorar su rendimiento y probamos su efectividad en conjuntos de datos reales comparándolos con el algoritmo de Sklearn. Sin embargo, los métodos presentados aquí no limitan la mejora de los algoritmos, así que tenga en cuenta que el código propuesto se puede mejorar aún más. En el próximo artículo, escribiremos un refuerzo basado en estos algoritmos.

Todo el exito!