Escribir XGBoost desde cero - parte 2: aumento de gradiente

Hola a todos!

En el último artículo, descubrimos cómo se organizan los árboles de decisión, y desde cero implementamos
algoritmo de construcción, optimizándolo y mejorándolo simultáneamente. En este artículo, implementaremos el algoritmo de aumento de gradiente y al final crearemos nuestro propio XGBoost. La narración seguirá el mismo patrón: escribimos un algoritmo, lo describimos, lo resumimos comparando los resultados de trabajar con análogos de Sklearn.

En este artículo, también se hará hincapié en la implementación en el código, por lo tanto, es mejor leer la teoría completa en otro (por ejemplo, en el curso ODS ), y ya con el conocimiento de la teoría, puede continuar con este artículo, ya que el tema es bastante complicado.



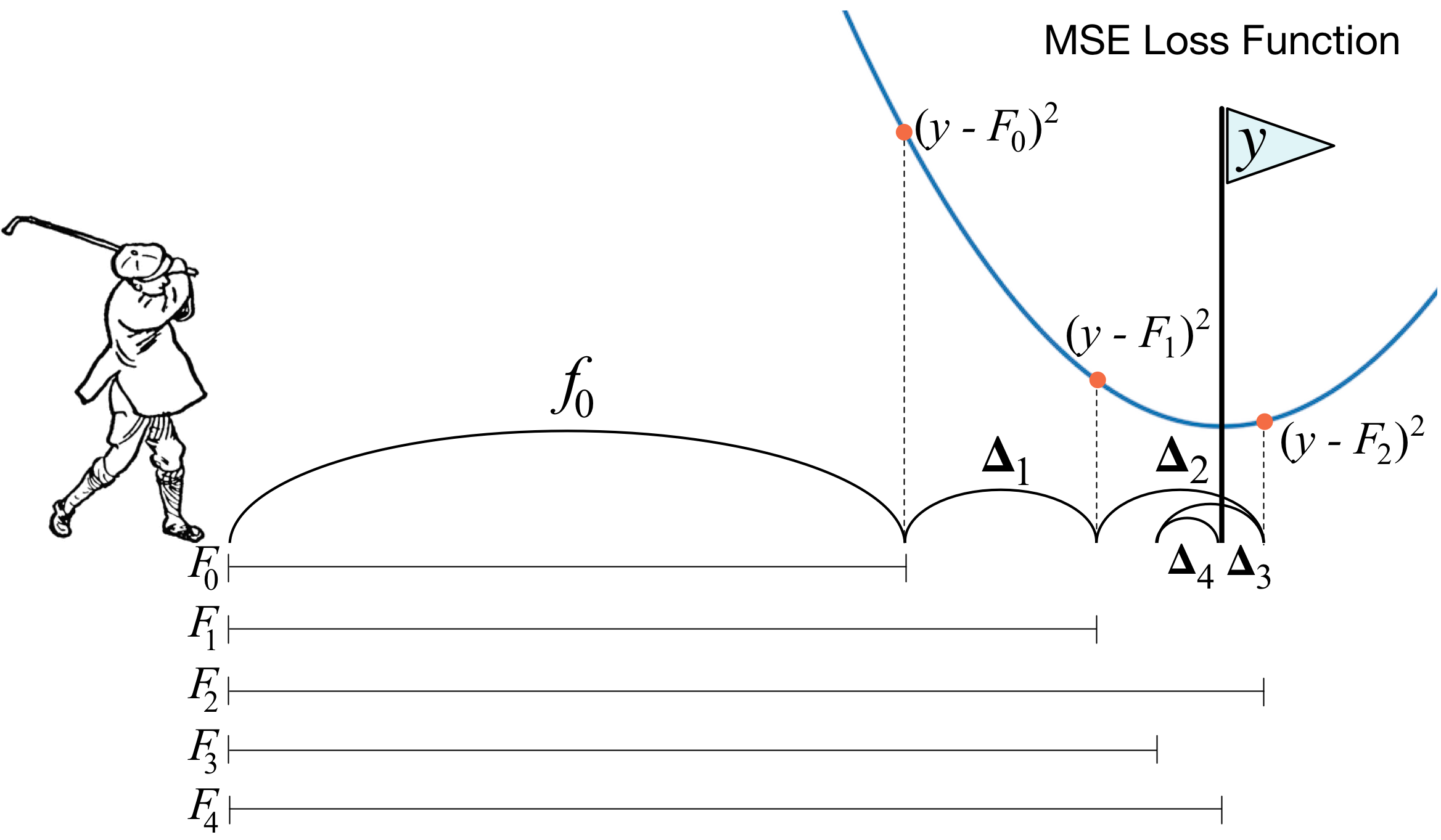
¿Qué es el aumento de gradiente? La imagen de un golfista describe perfectamente la idea principal. Para poder meter la pelota en el hoyo, el golfista realiza cada siguiente golpe teniendo en cuenta la experiencia de golpes anteriores; para él, esta es una condición necesaria para meter la pelota en el hoyo. Si es muy grosero (no soy un maestro del golf :)), con cada nuevo golpe lo primero que mira un golfista es la distancia entre la pelota y el hoyo después del golpe anterior. Y la tarea principal es reducir esta distancia con el próximo golpe.

El refuerzo se construye de una manera muy similar. Primero, necesitamos introducir la definición de "agujero", es decir, el objetivo por el que nos esforzaremos. En segundo lugar, debemos aprender a entender qué lado debemos vencer con un palo para acercarnos al objetivo. En tercer lugar, teniendo en cuenta todas estas reglas, debe encontrar la secuencia correcta de golpes para que cada uno de ellos reduzca la distancia entre la pelota y el hoyo.

Ahora damos una definición un poco más rigurosa. Presentamos el modelo de votación ponderada:

$$

$$h (x) = \ sum_ {i = 1} ^ nb_ia_i, x \ en X, b_i \ en R$$

Aqui $$$X$Es el espacio del que tomamos objetos, $$$b_i, a_i$- este es el coeficiente en frente del modelo y el modelo en sí, es decir, el árbol de decisión. Supongamos que ya en algún paso, usando las reglas descritas, fue posible agregar a la composición $$$T-1$algoritmo débil Para aprender a entender qué tipo de algoritmo debería estar en el paso $$$T$, presentamos la función de error:

$$$err (h) = \ sum_ {j = 1} ^ N L (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j)) \ rightarrow min_ {a_T, b_T}$

Resulta que el mejor algoritmo será el que pueda minimizar el error recibido en las iteraciones anteriores. Y dado que el impulso es gradiente, entonces esta función de error necesariamente debe tener un vector anti-gradiente a lo largo del cual pueda moverse en busca de un mínimo. Eso es todo!

Inmediatamente antes de la implementación, agregaré algunas palabras más sobre cómo exactamente se organizará todo con nosotros. Como en el artículo anterior, tomamos MSE como una pérdida. Calculemos su gradiente:

$$

$$mse (y, predecir) = (y - predecir) ^ 2 \\ \ nabla_ {predecir} mse (y, predecir) = predecir - y$$

Por lo tanto, el vector antigradiente será igual a $$$y - predice$. En el paso $$$i$Consideramos los errores del algoritmo obtenido en iteraciones anteriores. Luego, entrenamos nuestro nuevo algoritmo sobre estos errores, y luego lo agregamos a nuestro conjunto con un signo menos y algún coeficiente.

Ahora comencemos.

1. Implementación de la clase habitual de aumento de gradiente

import pandas as pd import matplotlib.pyplot as plt import numpy as np from tqdm import tqdm_notebook from sklearn import datasets from sklearn.metrics import mean_squared_error as mse from sklearn.tree import DecisionTreeRegressor import itertools %matplotlib inline %load_ext Cython %%cython -a import itertools import numpy as np cimport numpy as np from itertools import * cdef class RegressionTreeFastMse: cdef public int max_depth cdef public int feature_idx cdef public int min_size cdef public int averages cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef RegressionTreeFastMse left cpdef RegressionTreeFastMse right def __init__(self, max_depth=3, min_size=4, averages=1): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef np.float64_t mean1 = 0.0 cpdef np.float64_t mean2 = 0.0 cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef np.float64_t delta1 = 0.0 cpdef np.float64_t delta2 = 0.0 cpdef np.float64_t sm1 = 0.0 cpdef np.float64_t sm2 = 0.0 cpdef list index_tuples cpdef list stuff cpdef long idx = 0 cpdef np.float64_t prev_error1 = 0.0 cpdef np.float64_t prev_error2 = 0.0 cpdef long thres = 0 cpdef np.float64_t error = 0.0 cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 #   -   y self.value = y.mean() #   - mse     base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -  ,  ,    delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 #   ,  if self.feature_idx == -1: return #    self.left = RegressionTreeFastMse(self.max_depth - 1) self.left.value = left_value self.right = RegressionTreeFastMse(self.max_depth - 1) self.right.value = right_value #      idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #   self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

 class GradientBoosting(): def __init__(self, n_estimators=100, learning_rate=0.1, max_depth=3, random_state=17, n_samples = 15, min_size = 5, base_tree='Bagging'): self.n_estimators = n_estimators self.max_depth = max_depth self.learning_rate = learning_rate self.initialization = lambda y: np.mean(y) * np.ones([y.shape[0]]) self.min_size = min_size self.loss_by_iter = [] self.trees_ = [] self.loss_by_iter_test = [] self.n_samples = n_samples self.base_tree = base_tree def fit(self, X, y): self.X = X self.y = y b = self.initialization(y) prediction = b.copy() for t in tqdm_notebook(range(self.n_estimators)): if t == 0: resid = y else: #    resid = (y - prediction) #    if self.base_tree == 'Bagging': tree = Bagging(max_depth=self.max_depth, min_size = self.min_size) if self.base_tree == 'Tree': tree = RegressionTreeFastMse(max_depth=self.max_depth, min_size = self.min_size) #     tree.fit(X, resid) #        b = tree.predict(X).reshape([X.shape[0]]) self.trees_.append(tree) prediction += self.learning_rate * b #       if t > 0: self.loss_by_iter.append(mse(y,prediction)) return self def predict(self, X): #   –          pred = np.ones([X.shape[0]]) * np.mean(self.y) #    for t in range(self.n_estimators): pred += self.learning_rate * self.trees_[t].predict(X).reshape([X.shape[0]]) return pred 

Ahora construiremos la curva de pérdida en el conjunto de entrenamiento para asegurarnos de que en cada iteración realmente tengamos una disminución.

 GDB = GradientBoosting(n_estimators=50) GDB.fit(X,y) x = GDB.predict(X) plt.grid() plt.title('Loss by iterations') plt.plot(GDB.loss_by_iter) 

2. Empaquetamiento sobre árboles decisivos

Bueno, antes de comparar los resultados, hablemos sobre el procedimiento para embolsar árboles.

Aquí, todo es simple: queremos protegernos del reentrenamiento y, por lo tanto, con la ayuda del muestreo con retorno, promediaremos nuestras predicciones para no encontrar accidentalmente valores atípicos (por qué funciona de esta manera, lea el enlace mejor).

 class Bagging(): '''  Bagging -      . ''' def __init__(self, max_depth = 3, min_size=10, n_samples = 10): #super(CART, self).__init__() self.max_depth = max_depth self.min_size = min_size self.n_samples = n_samples self.subsample_size = None self.list_of_Carts = [RegressionTreeFastMse(max_depth=self.max_depth, min_size=self.min_size) for _ in range(self.n_samples)] def get_bootstrap_samples(self, data_train, y_train): #      indices = np.random.randint(0, len(data_train), (self.n_samples, self.subsample_size)) samples_train = data_train[indices] samples_y = y_train[indices] return samples_train, samples_y def fit(self, data_train, y_train): #    self.subsample_size = int(data_train.shape[0]) samples_train, samples_y = self.get_bootstrap_samples(data_train, y_train) for i in range(self.n_samples): self.list_of_Carts[i].fit(samples_train[i], samples_y[i].reshape(-1)) return self def predict(self, test_data): #        num_samples = test_data.shape[0] pred = [] for i in range(self.n_samples): pred.append(self.list_of_Carts[i].predict(test_data)) pred = np.array(pred).T return np.array([np.mean(pred[i]) for i in range(num_samples)]) 

Bueno, ahora como algoritmo básico no podemos usar un solo árbol, sino el embolsado de los árboles, así que nuevamente, nos protegeremos del reentrenamiento.

3. Resultados

Compara los resultados de nuestros algoritmos.

 from sklearn.model_selection import KFold import matplotlib.pyplot as plt from sklearn.ensemble import GradientBoostingRegressor as GDBSklearn import copy def get_metrics(X,y,n_folds=2, model=None): kf = KFold(n_splits=n_folds, shuffle=True) kf.get_n_splits(X) er_list = [] for train_index, test_index in tqdm_notebook(kf.split(X)): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] model.fit(X_train,y_train) predict = model.predict(X_test) er_list.append(mse(y_test, predict)) return er_list data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) er_boosting = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=40, base_tree='Tree' )) er_boobagg = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=40, base_tree='Bagging' )) er_sklearn_boosting = get_metrics(X,y,30,GDBSklearn(max_depth=3,n_estimators=40, learning_rate=0.1)) %matplotlib inline data = [er_sklearn_boosting, er_boosting, er_boobagg] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['Sklearn Boosting', 'Boosting', 'BooBag']) plt.grid() plt.show() 

Recibido:



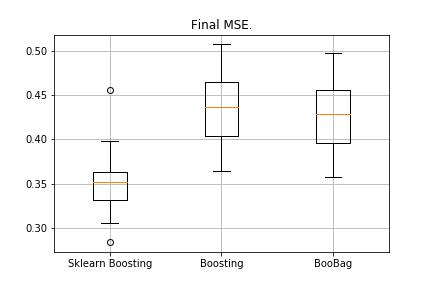
Todavía no podemos vencer al análogo de Sklearn, porque nuevamente no tenemos en cuenta muchos parámetros que se utilizan en este método . Sin embargo, vemos que el embolsado ayuda un poco.

No nos desesperemos, y pasemos a escribir XGBoost.

4. XGBoost

Antes de seguir leyendo, te recomiendo que te familiarices con el siguiente video , que explica muy bien la teoría.

Recuerde qué error minimizamos en el impulso normal:

$$

$$err (h) = \ sum_ {j = 1} ^ N L (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j))$$

XGBoost agrega explícitamente regularización a esta funcionalidad de error:

$$

$$err (h) = \ sum_ {j = 1} ^ NL (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j)) + \ sum_ {i = 1} ^ T \ omega (a_i)$$

¿Cómo considerar esta funcionalidad? Primero, lo aproximamos con la ayuda de una serie de Taylor de segundo orden, donde el nuevo algoritmo se considera como un incremento a lo largo del cual nos moveremos, y luego ya pintamos, dependiendo del tipo de pérdida que tengamos:

$$$f (x + \ delta x) \ thickapprox f (x) + f (x) '\ delta x + 0.5 * f (x)' '(\ delta x) ^ 2$

Es necesario determinar qué árbol consideraremos malo y cuál es bueno.

Recordemos con qué principio se construye la regresión $$$L_2$-regularización: cuanto más normales son los valores de los coeficientes antes de la regresión, peor, por lo tanto, es necesario que sean lo más pequeños posible.

En XGBoost, la idea es muy similar: un árbol es multado si la suma de la norma de valores en las hojas es muy grande. Por lo tanto, la complejidad del árbol se presenta de la siguiente manera:

$$

$$\ omega (a) = \ gamma Z + 0.5 * \ sum_ {i = 1} ^ {Z} w_i ^ 2$$

$$$w$- valores en las hojas, $$$Z$- número de hojas.

Hay fórmulas de transición en el video, no las mostraremos aquí. Todo se reduce al hecho de que elegiremos una nueva partición, maximizando la ganancia:

$$

$$Ganancia = \ frac {G_l ^ 2} {S_l ^ 2 + \ lambda} + \ frac {G_r ^ 2} {S_r ^ 2 + \ lambda} - \ frac {(G_l + G_r) ^ 2} {S_l ^ 2 + S_r ^ 2 + \ lambda} - \ gamma$$

Aqui $$$\ gamma, \ lambda$Son los parámetros numéricos de regularización, y $$$G_i, S_i$- las sumas correspondientes de la primera y segunda derivadas para esta partición.

Eso es todo, la teoría se expone muy brevemente, se dan los enlaces, ahora hablemos sobre cuáles serán los derivados si trabajamos con MSE. Es simple:

$$$mse (y, predecir) = (y - predecir) ^ 2 \\ \ nabla_ {predecir} mse (y, predecir) = predecir - y \\ \ nabla_ {predecir} ^ 2 mse (y, predecir) = 1$

¿Cuándo calcularemos la cantidad? $$$G_i, S_i$, solo agregue al primero $$$predic - y$y el segundo es solo la cantidad.

 %%cython -a import numpy as np cimport numpy as np cdef class RegressionTreeGain: cdef public int max_depth cdef public np.float64_t gain cdef public np.float64_t lmd cdef public np.float64_t gmm cdef public int feature_idx cdef public int min_size cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef public RegressionTreeGain left cpdef public RegressionTreeGain right def __init__(self, int max_depth=3, np.float64_t lmd=1.0, np.float64_t gmm=0.1, min_size=5): self.max_depth = max_depth self.gmm = gmm self.lmd = lmd self.left = None self.right = None self.feature_idx = -1 self.feature_threshold = 0 self.value = -1e9 self.min_size = min_size return def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef long idx = 0 cpdef long thres = 0 cpdef np.float64_t gl, gr, gn cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 cpdef np.float64_t best_gain = -self.gmm if self.value == -1e9: self.value = y.mean() base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 if self.max_depth <= 1: return dim_shape = X.shape[1] left_value = 0 right_value = 0 #    # -  -   mse, L = (y - pred)**2 # dL/dpred = pred - y,          - # dL^2/d^2pred = 1 - ,       for feat in range(dim_shape): idxs = np.argsort(X[:, feat]) gl,gr = y.sum(),0.0 N1, N2, thres = N, 0, 0 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] gl -= y[idx] gr += y[idx] #   gn = (gl**2) / (N1 + self.lmd) + (gr**2) / (N2 + self.lmd) gn -= ((gl + gr)**2) / (N1 + N2 + self.lmd) + self.gmm if thres < N - 1 and x == X[idxs[thres + 1], feat]: thres += 1 continue #     if (gn > best_gain) and (min(N1,N2) > self.min_size): flag = 1 best_gain = gn left_value = -gl / (N1 + self.lmd) right_value = -gr / (N2 + self.lmd) self.feature_idx = feat self.feature_threshold = x thres += 1 self.gain = best_gain if self.feature_idx == -1: return self.left = RegressionTreeGain(max_depth=self.max_depth - 1, gmm=self.gmm, lmd=self.lmd) self.left.value = left_value self.right = RegressionTreeGain(max_depth=self.max_depth - 1, gmm=self.gmm, lmd=self.lmd) self.right.value = right_value idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) #    if (self.left.left == None or self.right.left == None): if self.gain < 0.0: self.left = None self.right = None self.feature_idx = -1 def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

Una pequeña aclaración: para hacer que las fórmulas en los árboles con ganancia sean más hermosas, en impulso entrenamos al objetivo con un signo menos.

Modificamos ligeramente nuestro aumento, hacemos que algunos parámetros sean adaptativos. Por ejemplo, si notamos que la pérdida ha comenzado a alcanzar una meseta, entonces disminuimos la tasa de aprendizaje y aumentamos la profundidad máxima para los siguientes estimadores. También agregaremos un nuevo ensacado; ahora aumentaremos sobre los empaques de los árboles con ganancia:

 class Bagging(): def __init__(self, max_depth = 3, min_size=5, n_samples = 10): self.max_depth = max_depth self.min_size = min_size self.n_samples = n_samples self.subsample_size = None self.list_of_Carts = [RegressionTreeGain(max_depth=self.max_depth, min_size=self.min_size) for _ in range(self.n_samples)] def get_bootstrap_samples(self, data_train, y_train): indices = np.random.randint(0, len(data_train), (self.n_samples, self.subsample_size)) samples_train = data_train[indices] samples_y = y_train[indices] return samples_train, samples_y def fit(self, data_train, y_train): self.subsample_size = int(data_train.shape[0]) samples_train, samples_y = self.get_bootstrap_samples(data_train, y_train) for i in range(self.n_samples): self.list_of_Carts[i].fit(samples_train[i], samples_y[i].reshape(-1)) return self def predict(self, test_data): num_samples = test_data.shape[0] pred = [] for i in range(self.n_samples): pred.append(self.list_of_Carts[i].predict(test_data)) pred = np.array(pred).T return np.array([np.mean(pred[i]) for i in range(num_samples)]) 

 class GradientBoosting(): def __init__(self, n_estimators=100, learning_rate=0.2, max_depth=3, random_state=17, n_samples = 15, min_size = 5, base_tree='Bagging'): self.n_estimators = n_estimators self.max_depth = max_depth self.learning_rate = learning_rate self.initialization = lambda y: np.mean(y) * np.ones([y.shape[0]]) self.min_size = min_size self.loss_by_iter = [] self.trees_ = [] self.loss_by_iter_test = [] self.n_samples = n_samples self.base_tree = base_tree #  -       #   ,   lr   max_depth self.add_to_max_depth = 1 self.init_mse_board = 1.5 def fit(self, X, y): print (self.base_tree) self.X = X self.y = y b = self.initialization(y) prediction = b.copy() for t in tqdm_notebook(range(self.n_estimators)): if t == 0: resid = y else: resid = (y - prediction) if (mse(temp_resid,resid) < self.init_mse_board): self.init_mse_board /= 1.5 self.add_to_max_depth += 1 self.learning_rate /= 1.1 # print ('Alert!', t, self.add_to_max_depth) if self.base_tree == 'Bagging': tree = Bagging(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) resid = -resid if self.base_tree == 'Tree': tree = RegressionTreeFastMse(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) if self.base_tree == 'XGBoost': tree = RegressionTreeGain(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) resid = -resid tree.fit(X, resid) b = tree.predict(X).reshape([X.shape[0]]) # print (b.shape) self.trees_.append(tree) prediction += self.learning_rate * b temp_resid = resid return self def predict(self, X): #   –          pred = np.ones([X.shape[0]]) * np.mean(self.y) #    for t in range(self.n_estimators): pred += self.learning_rate * self.trees_[t].predict(X).reshape([X.shape[0]]) return pred 

5. Resultados

Por tradición, comparamos los resultados:

 data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) import matplotlib.pyplot as plt from sklearn.ensemble import GradientBoostingRegressor as GDBSklearn er_boosting_bagging = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=150,base_tree='Bagging')) er_boosting_xgb = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=150,base_tree='XGBoost')) er_sklearn_boosting = get_metrics(X,y,30,GDBSklearn(max_depth=3,n_estimators=150,learning_rate=0.2)) %matplotlib inline data = [er_sklearn_boosting, er_boosting_xgb, er_boosting_bagging] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['GdbSklearn', 'Xgboost', 'XGBooBag']) plt.grid() plt.show() 

La imagen será la siguiente:



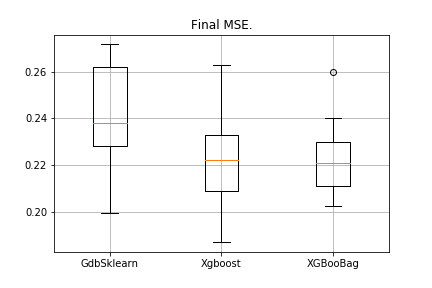
XGBoost tiene el error más bajo, pero XGBooBag tiene un error más abarrotado, que definitivamente es mejor: el algoritmo es más estable.

Eso es todo Realmente espero que el material presentado en dos artículos haya sido útil, y puedas aprender algo nuevo por ti mismo. Expreso mi especial agradecimiento a Dmitry por sus comentarios completos y su código fuente, a Anton por sus consejos y a Vladimir por sus difíciles tareas de estudio.

Todo el exito!