Llegó el próximo fin de semana, debe escribir un par de docenas de líneas de código y dibujar una imagen, pero ninguna es mejor. Entonces, el pasado fin de semana antes del último, mostré cómo
hacer el trazado de rayos e incluso
hacer explotar todo. Esto es sorprendente para muchos, pero los gráficos por computadora son muy simples, un par de cientos de líneas de C ++ desnudo son suficientes para crear imágenes interesantes.
El tema de la conversación de hoy es la visión binocular, y hoy ni siquiera podemos llegar a cien líneas de código. Ser capaz de renderizar escenas tridimensionales, sería una tontería pasar estereparaciones, hoy dibujaremos algo como esto:

La locura de los desarrolladores de
Magic Carpet me persigue. Para aquellos que no lo encontraron, este juego hizo posible renderizar en 3D tanto en anaglifo como en estereogramas
en la configuración principal, ¡solo disponible en el menú! Este cerebro explotó específicamente.
Paralaje
Entonces comencemos. Para empezar, ¿por qué nuestro aparato visual nos permite percibir la profundidad? Hay una palabra tan inteligente "paralaje". Si está en los dedos, concentrémonos en la pantalla. Todo lo que está en el plano de la pantalla para nuestro cerebro existe en una sola copia. Pero si de repente una mosca vuela frente a la pantalla, entonces (¡si no cambiamos nuestros ojos!) Nuestro cerebro lo registrará por duplicado. Y al mismo tiempo, la araña en la pared detrás de la pantalla también se bifurca, y la dirección de la bifurcación depende de si el objeto está delante del punto focal o detrás:
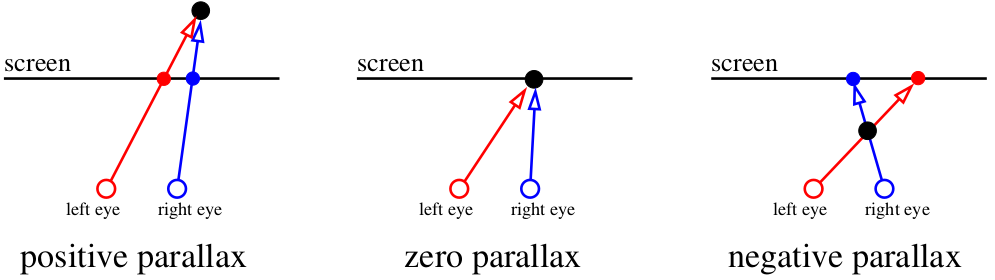
Nuestro cerebro es una máquina muy eficiente para analizar imágenes ligeramente diferentes. Utiliza la
disparidad para obtener información de profundidad de imágenes de retina bidimensionales para
estereopsis . Bueno, Dios los bendiga, con las palabras, ¡mejor dibujemos!
Asumamos que nuestra pantalla es una ventana al mundo virtual :)
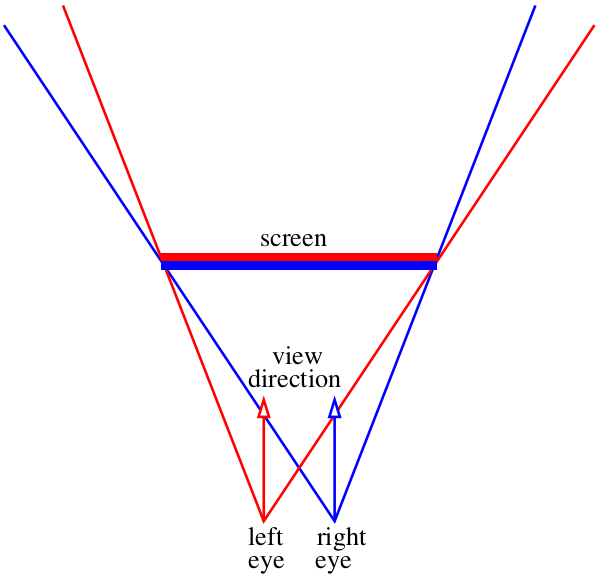
Nuestra tarea es dibujar dos imágenes con lo que será visible a través de esta "ventana". Habrá dos imágenes, una para cada ojo, en el diagrama de arriba las mostré con un "emparedado" rojo y azul. No nos molestemos aún cómo exactamente alimentamos estas imágenes al aparato visual, solo necesitamos guardar dos archivos. Me interesa específicamente cómo se pueden obtener estas imágenes con
nuestro rastreador de rayos .
Bueno, supongamos que la dirección de la mirada no cambia, es un vector (0,0, -1). Supongamos que podemos mover la posición de la cámara por la distancia interocular, ¿qué más? Hay una pequeña sutileza: el cono de vista a través de nuestra "ventana" es asimétrico. Y nuestro rastreador de rayos solo puede representar un cono de mirada simétrico:
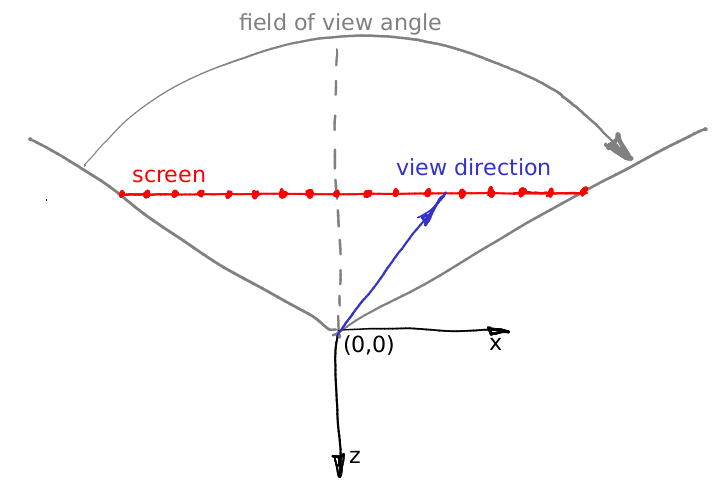
Que hacer Leer :)
De hecho, podemos hacer que las imágenes sean más anchas de lo que necesitamos y simplemente recortar el exceso:
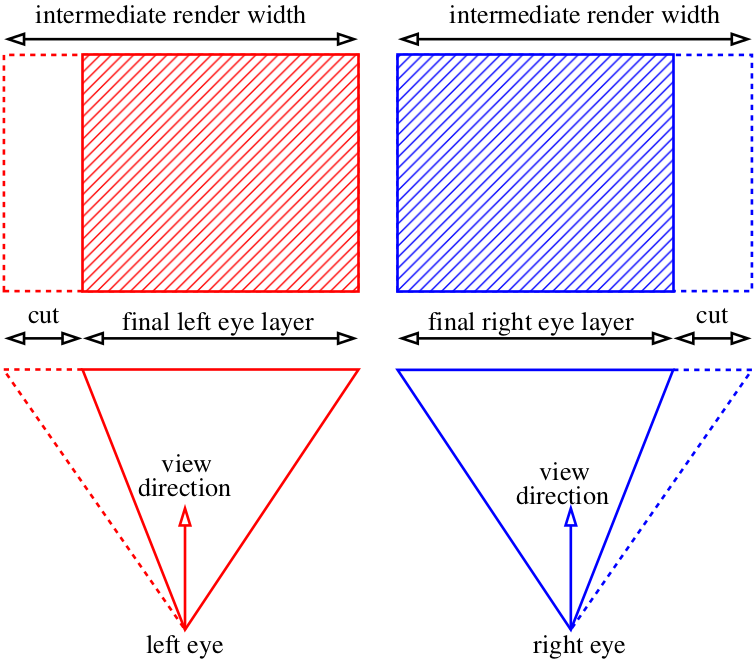
Anaglifo
Con el mecanismo de representación general, debe quedar claro, ahora es el momento de preguntarnos acerca de la entrega de la imagen a nuestro cerebro. Una de las opciones más simples son las gafas rojo-azul:

Simplemente hacemos que los dos pre-renders no sean negros sino blancos, escribamos la imagen izquierda en el canal rojo y la imagen derecha en azul. Obtienes la siguiente imagen:

El vidrio rojo cortará un canal, y el vidrio azul cortará otro, de modo que cada ojo recibirá su propia imagen y podremos ver el mundo en 3D. Estos son los
cambios en la confirmación principal del primer artículo , que muestran la configuración de la cámara para ambos ojos y el ensamblaje del canal.
Las representaciones anaglíficas son una de las formas más antiguas de ver (¡computadora!) Imágenes estéreo. Tienen muchas deficiencias, por ejemplo, mala reproducción del color (por cierto, intente grabar el canal verde del ojo derecho en el canal verde de la imagen final). Una ventaja: tales gafas están hechas fácilmente de materiales improvisados.
Estereoscopio
Con la proliferación de los teléfonos inteligentes, recordamos qué son los estereoscopios (que, por un segundo, se inventaron en el siglo XIX). Hace unos años,
Google sugirió usar dos lentes de centavo (desafortunadamente, no se hacen en la rodilla), un poco de cartón (por todas partes) y un teléfono inteligente (en el bolsillo) para obtener gafas de realidad virtual bastante tolerables:

En aliexpress, eran montones, cien rublos por pieza. En comparación con el anaglifo, no necesita hacer nada en absoluto, solo tome dos fotos y compóngalas una al lado de la otra,
aquí está el compromiso .

Estrictamente hablando, dependiendo de la lente, la
corrección de la distorsión de la lente puede ser necesaria, pero no me molesté en absoluto y se ve muy bien en mis lentes. Pero si realmente necesita aplicar una distorsión previa en forma de barril que compense la distorsión de la lente, entonces así es como se ve mi teléfono inteligente y mis lentes:

Estereogramas
Pero, ¿qué pasa si no quieres usar dispositivos adicionales? Entonces solo hay una opción: adormecer. En términos generales, la imagen anterior es suficiente para ver estéreo, solo use el truco para mirar estéreo. Hay dos principios para ver estereogramas: mueva los ojos o separe los ojos. Entonces dibujé un diagrama en el que le muestro cómo puede ver la imagen anterior. La imagen anterior es doble, dos barras rojas en el diagrama muestran dos imágenes en la retina izquierda, dos azules en la derecha.
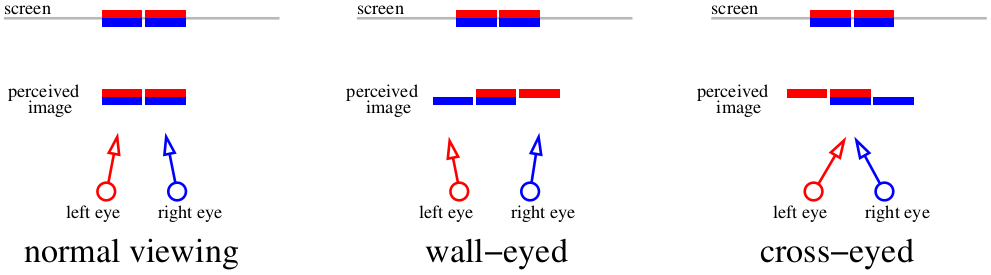
Si enfocamos nuestros ojos en la pantalla, de cuatro imágenes obtenemos dos. Si entrecerramos los ojos hacia la nariz, es muy posible mostrarle al cerebro "tres" imágenes. Y viceversa, si abre los ojos, también puede obtener "tres" imágenes. La superposición de imágenes centrales le dará al cerebro un efecto estéreo.
Estos métodos se administran a diferentes personas de diferentes maneras, por ejemplo, no sé cómo mover los ojos, pero me reproduzco fácilmente. Es importante que el estereograma construido para un método se vea de la misma manera, de lo contrario se obtiene un mapa de profundidad invertido (ver paralaje negativo y positivo). El problema con este método de visualización estéreo es que es muy difícil mover los ojos
fuertemente en relación con el estado normal, por lo que debe contentarse con imágenes pequeñas. ¿Y si quieres unos grandes? Sacrifiquemos completamente el color, y queramos solo una percepción de profundidad. Mirando hacia el futuro, aquí está la imagen que tenemos al final de esta parte:

Este estereograma está diseñado para "diluir" los ojos (estereograma de ojos de pared). Para aquellos que prefieren la forma inversa de ver,
tome una foto aquí . Si no está acostumbrado a los estereogramas, pruebe diferentes condiciones: una imagen de pantalla completa, una imagen pequeña, luz brillante, oscuridad. La tarea es abrir los ojos para que las dos tiras vorticales adyacentes coincidan. La forma más fácil de enfocarse en la esquina superior izquierda es Ella es plana. Por ejemplo, estoy rodeado por el entorno del Habr, abro la imagen en pantalla completa. ¡No olvides quitarle el mouse!
No se conforme con el efecto 3D defectuoso. Si solo eres vagamente consciente de las formas redondeadas en medio de puntos aleatorios junto con algunos efectos 3D tenues, ¡esta es ciertamente una ilusión incompleta! Si mira correctamente, las bolas deben salir claramente del plano de la pantalla al espectador, el efecto debe ser estable y mantenido debido al estudio constante y detallado de cada parte de la imagen, tanto el primer plano como el fondo. La estereopsis tiene histéresis: tan pronto como obtienes una imagen estable, se vuelve más clara cuanto más tiempo miras. Cuanto más lejos esté la pantalla de los ojos, mayor será el efecto de profundidad.
Este estereograma se dibujó de acuerdo con el método propuesto hace un cuarto de siglo por Thimbleby et al. En su artículo "
Visualización de imágenes en 3D: algoritmos para estereogramas de puntos aleatorios de una sola imagen ".
Punto de partida
El punto de partida para renderizar estereogramas es un mapa de profundidad (nos olvidamos del color).
Aquí hay una confirmación que muestra esa imagen:

Las profundidades en nuestro render están cortadas por los planos cercanos y lejanos, es decir, el punto más alejado de mi mapa tiene una profundidad de 0, el más cercano.
Principio básico
Deje que nuestros ojos estén a una distancia d de la pantalla. Coloque el plano lejano (imaginario) (z = 0) a la misma distancia detrás de la pantalla. Elegimos una constante μ, que determina la posición del plano cercano (z = 0): estará a una distancia μd de la lejana. Elegí μ = 1/3 en mi código. Total, nuestro mundo entero vive a una distancia de d-μd a d detrás de la pantalla. Tengamos una distancia e definida entre los ojos (en píxeles, en mi código elegí 400 píxeles).
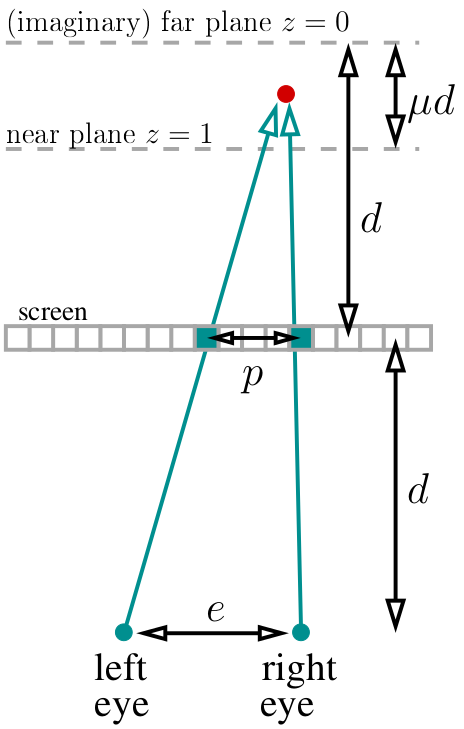
Si observamos el punto de nuestro objeto marcado en rojo en el diagrama, entonces dos píxeles marcados en verde deberían tener el mismo color en el estereograma. ¿Cómo encontrar la distancia entre estos píxeles? Muy simple Si el punto proyectado actual tiene una profundidad de z, entonces la relación de paralaje a la distancia entre los ojos es igual a la relación de las profundidades correspondientes: p / e = (d-dμz) / (2d-dμz). Por cierto, tenga en cuenta que d se está reduciendo y no está involucrado en ningún otro lugar. Es decir, p / e = (1-μz) / (2-μz), lo que significa que el paralaje es igual a p = e * (1-μz) / (2-μz) píxeles.
Es decir, el principio básico de la construcción de un estereograma: revisamos todo el mapa de profundidad, para cada valor de profundidad determinamos qué píxeles deben tener el mismo color y escribimos esto en nuestro sistema de restricciones. Luego comenzamos desde una imagen arbitraria e intentamos cumplir con todas las restricciones impuestas previamente.
Prepara la foto original
En esta etapa, prepararemos una imagen en la que luego impondremos restricciones de paralaje.
Aquí, comprométete , dibuja esta imagen:

Tenga en cuenta que, en general, los colores son aleatorios, excepto que pongo rand () * sin en el canal rojo para proporcionar ondas periódicas. Estas ondas están hechas con una distancia de 200 píxeles, este (con μ = 1/3 y e = 400 seleccionados) es el valor de paralaje máximo en nuestro mundo, también es un plano distante. Estas ondas son opcionales, pero facilitarán el enfoque de visión necesario.
Renderizar estereograma
En realidad, el código completo relacionado con el estereograma se ve así:
int parallax(const float z) { const float eye_separation = 400.;
En todo caso, entonces
comprométete aquí . La función int parallax (const float z) proporciona la distancia entre píxeles del mismo color para el valor de profundidad actual. Representamos el estereograma línea por línea, ya que las líneas son independientes entre sí (no tenemos paralaje vertical). Por lo tanto, el bucle principal simplemente recorre todas las líneas; Para cada uno de ellos, comenzamos con un conjunto completo e ilimitado de píxeles, sobre los cuales impondremos restricciones de igualdad por pares, y al final tendremos un cierto número de grupos de píxeles (desconectados) del mismo color. Por ejemplo, un píxel con índice a la izquierda y un píxel con índice a la derecha deberían terminar siendo los mismos.
¿Cómo almacenar este conjunto de restricciones? La respuesta más simple es la
unión: encontrar la estructura de datos . No lo describiré, son solo tres líneas de código, puedes leerlo en Wikipedia. La idea principal es que para cada grupo tendremos un cierto "responsable", también es un píxel raíz, lo dejaremos del mismo color que en la imagen original y volveremos a pintar todos los demás píxeles en el grupo:
for (size_t i=0; i<width; i++) {
Conclusión
Bueno, en realidad, eso es todo. Veinte líneas de código, ¡y nuestro estereograma está listo, rompa los ojos y la cabeza, haga dibujos! Por cierto, solo los colores aleatorios en un estereograma son generalmente un lujo, en principio, si lo intentas, también puedes transmitir parcialmente el color de nuestra imagen.
Otros sistemas de visualización estéreo, por ejemplo,
relacionados con la polarización , saqué de la discusión, ya que van más allá del presupuesto de cien rublos. Si te pierdes algo, agrega y corrige!