Tras conocernos en 2019 y descansar un poco del desarrollo de nuevas funciones para Smart IDReader, recordamos que no habíamos escrito nada sobre procesadores domésticos durante mucho tiempo. Por lo tanto, decidimos corregir con urgencia y mostrar otro sistema de reconocimiento en Elbrus.
Como sistema de reconocimiento, el sistema de reconocimiento de objetos de pintura se consideró "bajo condiciones no controladas por el método con entrenamiento según un ejemplo" [1]. Este sistema crea una descripción de la imagen basada en puntos singulares y sus descriptores, que busca en una base de datos indexada de imágenes. Analizamos el rendimiento de este sistema e identificamos la parte del algoritmo de bajo nivel que consume más tiempo, que luego se optimizó utilizando las herramientas de la plataforma Elbrus.
¿De qué tipo de sistema de reconocimiento estamos hablando?
Actualmente, la mayoría de los museos y galerías usan varias herramientas para familiarizarse independientemente con la exposición. Junto con las guías de audio clásicas, las aplicaciones móviles que utilizan métodos de procesamiento y análisis de imágenes se han generalizado. Algunas de estas aplicaciones reconocen códigos gráficos para exhibiciones (barra o QR) [2], para otras [3-4] los datos de entrada son marcos de fotos o videos con una exhibición tomada en primer plano (Smartify, Artbit). Por supuesto, las "guías móviles" de esta última categoría son más convenientes para el usuario [5] que las soluciones con entrada manual del número de exhibición o reconocimiento QR: el número y el código son bastante pequeños, y su búsqueda y entrada requiere acciones adicionales que no están relacionadas con la revisión de la exposición. Es un sistema que consideraremos.
La tarea de reconocer pinturas en imágenes se formuló de la siguiente manera. Solicitar imagen Q debe asignarse a una de las clases C = \ {C_i \} _ {i \ en [0, N]}C = \ {C_i \} _ {i \ en [0, N]} donde Ci - clase de imagen i exponer en i en[1,N] , C0 - una clase de otras imágenes correspondientes al valor "imagen desconocida". Para cada Ci conjunto de imágenes de referencia Ti .
Además, nos guiamos por los siguientes supuestos:
- Solicitar imagen Q obtenido mediante la cámara de un dispositivo móvil por un usuario no preparado durante una excursión, por lo tanto:
a) puede contener defectos visuales: deslumbramiento, áreas desenfocadas, ruido;
b) el ángulo, el encuadre, la iluminación y el balance de color son desconocidos (Fig. 1a);
c) objetos extraños, como paisajes, marcos de cuadros, visitantes, pueden estar presentes en la imagen (Fig. 1b). - Imagen de referencia T Es una imagen de alta resolución con una proyección frontal de una imagen o su reproducción digital. El estándar no contiene objetos extraños y defectos visuales. Los estándares pueden ser, por ejemplo, páginas escaneadas cualitativamente de álbumes de arte (Fig. 2).
- La imagen (tanto en la solicitud como en el estándar) puede aplicarse a cualquier estilo: realismo,
impresionismo, abstraccionismo, gráficos fractales, etc. - Numero de clases N corresponde al tamaño de la colección y para una galería puede alcanzar
cientos de miles de exhibiciones [6].

Figura 1 - Ejemplos de solicitudes de imágenes a) una imagen se fotografía desde lejos con poca luz, b) un visitante está en el marco.

Figura 2 - Ejemplos de imágenes de referencia para pinturas a) Claude Monet "De Voorzaan en de Westerhem", b) Salvador Dali "La persistència de la memòria"
La idea principal de nuestra solución a este problema se basa en construir una descripción especial de la imagen a partir de la imagen de entrada, que luego se utiliza para buscar esta imagen en la base de datos de descripciones de imágenes de referencia de imágenes de alta resolución que no están sujetas a distorsiones geométricas y otros defectos de foto. Las coordenadas de los puntos singulares encontrados utilizando el algoritmo YACIPE [7] y sus descriptores RFD actúan como tal descripción.
Para cada referencia Ti construir una descripción y luego indexarla; para cada punto de la descripción, ingresamos un registro del formulario langlei,fi rangle en un árbol de búsqueda de agrupamiento jerárquico aleatorio [8], que le permite realizar una búsqueda aproximada de los vecinos más cercanos con una ganancia de velocidad significativa en comparación con una búsqueda lineal. La distancia de Hamming se usa como métrica, ya que usamos un descriptor binario.
El proceso de reconocimiento es el siguiente:
En la imagen de solicitud Q área de pintura QL prelocalizado utilizando el supuesto de la rectangularidad del marco. La búsqueda de zonas se lleva a cabo utilizando el algoritmo de búsqueda rápida de cuadrángulos [9] con la restricción de la relación de aspecto eliminada. Esto evita los siguientes problemas:
- descripción insuficiente del área de la imagen debido a objetos extraños en el marco, que pueden tener puntos especiales con las mejores calificaciones;
- costos computacionales para comparar descriptores de áreas ubicadas fuera de la imagen;
- un desajuste significativo en la escala y el ángulo entre el estándar en la base de datos y la imagen de la imagen, lo que conduce a un resultado incorrecto de descriptores coincidentes.
La imagen en la zona encontrada se normaliza proyectivamente:
Q∗=H(QL),
donde H - transformación proyectiva.
Crea una descripción compacta w∗ :
a) la imagen se reduce a un tamaño estándar mientras se mantienen las proporciones para que el algoritmo sea más resistente a la escala;
b) un filtro gaussiano suprime el ruido de alta frecuencia;
c) los puntos singulares se calculan en la imagen resultante, su número está limitado artificialmente a M Lo mejor por evaluación interna de YACIPE;
d) se calculan los descriptores de color similares a RFD de las vecindades de los puntos singulares encontrados, ya que en nuestra tarea era importante guardar información sobre las características de color de las imágenes de entrada. Por ejemplo, las imágenes en la Fig. 3 sería extremadamente difícil distinguir sin él;
d) así, la descripción de la imagen I se puede representar como: w ^ * = \ {\ langle p_i, f_i) \ rangle \} _ {i \ in [1, M]}w ^ * = \ {\ langle p_i, f_i) \ rangle \} _ {i \ in [1, M]} donde pi= langlexi,yi rangle Son las coordenadas del i-ésimo punto singular, y fi Es el identificador del vecindario del i-ésimo punto singular.
Para cada entrada langlep,f rangle inw∗ el índice realiza una búsqueda aproximada de los vecinos más cercanos del descriptor f . El procedimiento de votación se aplica a los descriptores encontrados: el descriptor fi agrega una voz al estándar Ti . Luego, se seleccionan los candidatos K candidatos con el mayor número de votos.
Para cada uno de K las opciones seleccionadas usando el algoritmo RANSAC, se realiza una búsqueda de transformación proyectiva H traducir, dentro de un error geométrico dado delta puntos de consulta Q∗ a puntos de referencia T . Par de puntos langlep,p′ rangle con descriptores cercanos se considera una coincidencia válida si:
left|H(p)−p′ derecha|< delta,p inw∗,p′ inwT
Como resultado final, se selecciona el estándar Tb para el cual el número de comparaciones correctas resultó ser el máximo. Si es menor que un cierto valor umbral R , el resultado será la respuesta "imagen desconocida" para evitar falsos positivos (por ejemplo, en imágenes para las que no hay una descripción del estándar en la base de datos de búsqueda).


Figura 3 - Claude Monet. Catedral de Rouen, Fachada Oeste, Luz del sol (izquierda) y Catedral de Rouen, Portal y Torre Saint-Romain en el Sol (derecha).
Una de las partes principales del sistema es la búsqueda de descriptores cercanos utilizando la distancia de Hamming como métrica. Como se calcula muchas veces, esta etapa lleva mucho tiempo computacionalmente y toma el 65% del tiempo del sistema. Por eso lo optimizamos.
Una descripción muy pequeña de la arquitectura de Elbrus.
La arquitectura del procesador de Elbrus utiliza el principio de una palabra de comando amplia (Very Long Instruction Word, VLIW). Esto significa que el procesador ejecuta instrucciones en grupos, y dentro de cada grupo no hay dependencias y estas instrucciones se ejecutan en paralelo. Cada uno de estos grupos se llama una palabra de comando amplia. Las palabras de comando amplias son generadas por un compilador optimizador, que hace posible un análisis más detallado del código fuente, lo que lleva a una paralelización más eficiente [10].
Una característica de la arquitectura de Elbrus son los métodos de trabajo con memoria. Además de tener un caché que optimiza el tiempo de acceso a la memoria, los procesadores Elbrus admiten un método de hardware y software para pre-paginar datos. Este método permite predecir accesos a la memoria y bombear datos al búfer de datos preliminar. El hardware del procesador incluye un dispositivo especial para acceder a los arreglos (Array Access Unit, AAU), pero el compilador determina la necesidad de intercambio, lo que genera instrucciones especiales para AAU. El uso de un dispositivo de intercambio es más eficiente que colocar elementos de la matriz en la memoria caché, ya que los elementos de la matriz a menudo se procesan secuencialmente y rara vez se usan más de una vez [11]. Sin embargo, debe tenerse en cuenta que el uso del búfer de pre-paginación en Elbrus solo es posible cuando se trabaja con datos alineados. Debido a esto, la lectura / escritura de datos alineados ocurre mucho más rápido que las operaciones correspondientes para datos no alineados.
Además, los procesadores Elbrus admiten varios tipos de paralelismo además del paralelismo en el nivel de comando: paralelismo SIMD, paralelismo de flujos de control, paralelismo de tareas en un complejo de máquinas múltiples. De particular interés para nosotros es la simultaneidad SIMD.
Características del uso del procesador de expansión SIMD Elbrus
El uso de extensiones SIMD se puede llevar a cabo en dos modos: automático y directo. En el primer caso, el compilador realiza completamente la paralelización de las operaciones sin la participación del desarrollador. Este modo es limitado, ya que el código optimizado debe repetir completamente el comportamiento del código fuente, incluido el comportamiento cuando se desborda, se redondea, etc. En este caso, el comportamiento de las instrucciones de extensión SIMD puede diferir en estos aspectos de las instrucciones del procesador. Además, los algoritmos utilizados en los compiladores son imperfectos y no siempre pueden realizar una paralelización eficiente. Sin embargo, los desarrolladores también pueden acceder a los comandos de extensión SIMD directamente utilizando intrínsecos. Los intrínsecos son funciones cuyas llamadas son reemplazadas por el compilador con código de alto rendimiento para una plataforma dada, en particular, con comandos de extensión SIMD. Los procesadores Elbrus-4C y Elbrus-8C admiten un conjunto de intrínsecos, para los cuales el tamaño del registro es de 64 bits. Incluye operaciones para la conversión de datos, inicialización de elementos vectoriales, operaciones aritméticas, operaciones lógicas bit a bit, permutación de elementos vectoriales, etc.
Al usar intrínsecos en la plataforma Elbrus, se debe prestar especial atención al acceso a la memoria, ya que las tareas prácticas, por ejemplo, las tareas de procesamiento de imágenes, a menudo requieren una lectura desequilibrada de datos en un registro de 64 bits. Tal lectura en sí misma es ineficiente, ya que requiere un par de comandos de lectura y un comando posterior para formar un bloque de datos, pero, lo que es más importante, no se puede usar un buffer de intercambio de matriz para aumentar la velocidad de acceso a datos. Sin embargo, vale la pena señalar que el problema del acceso ineficiente a los datos no alineados es relevante para los procesadores Elbrus-4C y Elbrus-8C, mientras que para el nuevo Elbrus-8CV con la quinta versión del sistema de comando, está parcialmente resuelto. Se espera que los procesadores Elbrus con la sexta versión del sistema de instrucciones se resuelvan por completo.
Sin embargo, en los procesadores Elbrus-4C y Elbrus-8C, el procesamiento de datos de bajo nivel se realiza de manera eficiente teniendo en cuenta la alineación. Por ejemplo, para las matrices numéricas, puede constar de varias etapas: procesar la parte inicial (hasta el borde de alineación de 64 bits de una de las matrices), procesar la parte principal utilizando el acceso alineado a la memoria y procesar los elementos restantes de la matriz. Dado que analizar los punteros durante la compilación no es una tarea trivial, puede usar el –faligned compilador con –faligned , con el que todas las operaciones de acceso a la memoria se realizan de forma alineada.
La siguiente característica del uso de intrínsecos en la plataforma Elbrus está directamente relacionada con su arquitectura VLIW. Debido a la presencia de varios dispositivos de lógica aritmética (ALU), que funcionan en paralelo y se cargan al formar palabras de comando amplias, se pueden ejecutar varios comandos simultáneamente. En total, los procesadores Elbrus-4C y Elbrus-8C tienen seis ALU que pueden usarse como parte de un equipo amplio, pero cada ALU admite su propio conjunto de intrínsecos. Las operaciones simples, como agregar o multiplicar elementos en registros de 64 bits, como regla, admiten dos ALU. Esto significa que el procesador Elbrus puede ejecutar dos de esas instrucciones en un solo ciclo de reloj. Para hacer esto, el ciclo de ejecución debe usarse en código ejecutable. El compilador de optimización para la plataforma Elbrus admite pragma #pragma unroll(n) , que permite el despliegue de n iteraciones de bucle.
Un ejemplo de la implementación de la función de suma teniendo en cuenta estas características se puede encontrar en nuestro artículo anterior.
Los experimentos
¡Hurra, el texto ha terminado y finalmente lanzaremos algo en Elbrus!
Primero, consideramos por separado la distancia de Hamming. Sin más preámbulos, comparamos vectores de dos bits de datos aleatorios. Los valores binarios se empaquetaron en matrices de enteros de 8 bits, y por simplicidad pensamos que las longitudes de los vectores originales son múltiplos de 8. Como de costumbre, el código está escrito en C ++, compilado por lcc 1.21.24, un compilador optimizador de Elbrus.
Escribimos varias implementaciones de Hamming distance, que tuvieron en cuenta secuencialmente las características de los procesadores Elbrus. Se veían así:
- Se utiliza un XOR bit a bit entre enteros de 8 bits y una tabla de valores calculados previamente. Esta es una implementación básica sin intrínsecos y otros trucos.
- Utiliza XOR entre enteros de 32 bits e intrínsecos para calcular el número de unidades en un entero de 32 bits: popcnt32. No se realizó la alineación de límite de 32 bits.
- Utiliza XOR entre enteros de 64 bits e intrínsecos para calcular el número de unidades en un entero de 64 bits: popcnt64. No se realizó la alineación del borde de 64 bits.
- Utiliza XOR entre enteros de 64 bits e intrínsecos para calcular el número de unidades en un entero de 64 bits: popcnt64. El acceso a la memoria se realiza de manera alineada. Dado que las direcciones iniciales de las matrices pueden tener una alineación diferente, cuando se lee una de las matrices, se leen dos bloques vecinos de 64 bits y se forma el bloque de 64 bits necesario a partir de ellos.
- Utiliza XOR entre enteros de 64 bits e intrínsecos para calcular el número de unidades en un entero de 64 bits: popcnt64. El acceso a la memoria se realiza de manera alineada. Dado que las direcciones iniciales de las matrices pueden tener una alineación diferente, cuando se lee una de las matrices, se leen dos bloques vecinos de 64 bits y se forma el bloque de 64 bits necesario a partir de ellos. Además, se
-faligned el -faligned compilador -faligned . - Utiliza XOR entre enteros de 64 bits e intrínsecos para calcular el número de unidades en un entero de 64 bits: popcnt64. El acceso a la memoria se realiza de manera alineada. Dado que las direcciones iniciales de las matrices pueden tener una alineación diferente, cuando se lee una de las matrices, se leen dos bloques vecinos de 64 bits y se forma el bloque de 64 bits necesario a partir de ellos. Además, se
-faligned compilador firmado y los pragmas del compilador #pragma unroll(2) unroll #pragma unroll(2) (para usar ambas ALU disponibles para calcular popcnt64) y #pragma loop count(1000) (para habilitar optimizaciones de #pragma loop count(1000) adicionales).
Los resultados de las mediciones de tiempo se muestran en la tabla 1.
Tabla 1. Tiempo para calcular la distancia de Hamming entre dos conjuntos de números binarios empaquetados de longitud 10 ^ 5 en una máquina con un procesador Elbrus-4C. Tiempo promedio de 10 ^ 5 comienza.
| No | Un experimento | Tiempo, ms |
|---|
| 1 | tabla de valores calculados | 141,18 |
| 2 | popcnt32, sin alineación | 125,54 |
| 3 | popcnt64, sin alineación | 58,00 |
| 4 4 | alineación popcnt64 | 17.36 |
| 5 5 | alineación -faligned , -faligned | 17.15 |
| 6 6 | popcnt64, alineación, -faligned, pragma unroll | 12,23 |
Puede ver que todas las optimizaciones consideradas llevaron a una disminución de 11.5 veces en el tiempo de ejecución. Vale la pena señalar que el uso de intrínsecos con acceso desequilibrado a la memoria mostró una aceleración solo 1.13 veces (para popcnt32) y 2.4 veces (para popcnt64), mientras que la contabilidad de la alineación de datos condujo al uso del buffer de intercambio de matriz APB con la ayuda de la cual fue posible lograr una aceleración de otras 3.4 veces (58 ms versus 17.15 ms). A pesar del hecho de que el uso del indicador firmado no mostró una ganancia de rendimiento significativa en el ejemplo anterior, en algoritmos más complejos puede haber una situación en la que el compilador no puede analizar el código fuente lo suficientemente profundo como para generar comandos para APB. Tener en cuenta el número real de ALU especializadas nos permitió acelerar los cálculos otras 1,4 veces.
¡No tan mal! Como comparamos hasta 6 opciones de implementación, le damos el pseudocódigo del último y más rápido:
: 8- A B, T, T[i] i : res, A B offset ← A 64- effective_len ← , 64- for i from 1 to offset: res ← res + T[xor(A[i] , B[i])] v_a ← 64- , A[offset+1] v_b1 ← 64- , B[offset] v_b2 ← 64- , v_b1 // 64- for i from offset to effective_len: v_b ← align(v_b1, v_b2) // 64- , v_a res ← res + popcnt64(xor(v_a, v_b)) v_a ← 64- v_b1 ← v_b2 v_b2 ← 64- //
Sería genial de una vez por todas acelerar el cálculo de la distancia de Hamming en 11,5 veces, pero en la vida todo es un poco más complicado: tal implementación tendrá una ventaja solo con longitudes de matrices suficientemente grandes. En la fig. La Figura 4 presenta una comparación del tiempo de cálculo utilizando la tabla de valores calculados previamente y nuestra implementación final. Puede ver que con nuestra versión comienza a ganar solo comenzando con longitudes superiores a 400 bytes, y esto también debe tenerse en cuenta al optimizar en Elbrus.
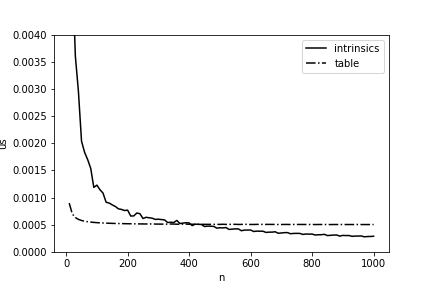
Figura 4 - Tiempo promedio (por 1 byte) para calcular la distancia de Hamming entre dos matrices dependiendo de su longitud en Elbrus-4C.
Eso es todo, ahora estamos listos para medir el tiempo de funcionamiento de todo el sistema. Medimos el tiempo promedio de procesamiento de solicitudes (excluyendo la carga de imágenes) para 933 solicitudes. Al compilar una descripción compacta de la imagen, se utilizó un descriptor binario a color RFD de 5328 bits. Consistió en 3 descriptores RFD grises concatenados de 1776 bits calculados para cada canal de la sección de imagen de entrada. Por un lado, tales descriptores largos no satisfacen con una alta velocidad de cálculo y comparación; por otro lado, proporcionan una calidad de trabajo suficientemente alta. Sin embargo, hay buenas noticias: ¡podemos usar la implementación rápida de la distancia de Hamming para compararlas! Las longitudes de las matrices comparadas son 666 bytes, que es más que el valor umbral de 400 bytes para Elbrus-4C.
Los resultados de la medición se muestran en la Tabla 2. Se puede ver que solo una implementación rápida de la distancia de Hamming proporciona un procesamiento de consultas 1.5 veces más rápido. También vale la pena señalar que esta optimización no cambia los resultados de los cálculos y, por lo tanto, la calidad del reconocimiento.
Tabla 2. Tiempo promedio de procesamiento de una solicitud a un sistema de reconocimiento de objetos de pintura en condiciones no controladas.
| Un experimento | Tiempo de solicitud, s | El cálculo de la distancia de Hamming tomó | Tiempos de aceleración |
|---|
| Implementación base | 2,81 | 63% | - |
| Implementación rápida | 1,87 | 40% | 1,5 |
Conclusión
En este artículo, hablamos un poco sobre la estructura del sistema de reconocimiento para pintar objetos en condiciones no controladas y una vez más mostramos cómo las manipulaciones de bajo nivel pueden aumentar significativamente su velocidad en la plataforma Elbrus. Entonces, la implementación propuesta de la distancia de Hamming funciona un orden de magnitud (!) Más rápido que la implementación usando una tabla de valores precalculados con una longitud suficientemente grande de los vectores de entrada, ¡y todo el sistema se aceleró por un factor de 1.5! Para lograr este resultado, se utilizaron extensiones SIMD, y se tuvieron en cuenta las características de arquitectura y acceso a la memoria de los procesadores Elbrus-4C y Elbrus-8C. Estos resultados muestran que los procesadores Elbrus contienen recursos significativos para una operación eficiente, que no se utilizan por completo en ausencia de una optimización especialmente realizada. Sin embargo, se espera que los métodos de acceso a la memoria se mejoren en los nuevos procesadores Elbrus, lo que permitirá que algunas de estas optimizaciones se realicen automáticamente y facilitará enormemente la vida de los desarrolladores.
Literatura
[1] N.S. Skoryukina, A.N. Milovzorov, D.V. Field, V.V. Arlazarov El método de reconocimiento de objetos de pintura en condiciones no controladas con entrenamiento según un ejemplo // Transacciones de ISA RAS. - Número especial, 2018 - p. 5-15.
[2] Pérez-Sanagustín M. y col. Uso de códigos QR para aumentar la participación del usuario en espacios tipo museo // Computadoras en el comportamiento humano. - 2016. - T. 60. - S. 73-85. doi: 10.1016 / j.chb.2016.02.02.012
[3] Antoshchuk S. G., Godovichenko N. A. Análisis de las características puntuales de la imagen en el sistema Mobile Virtual Guide // Pratsi. - 2013. - No. 1 (40). - S. 67-72.
[4] Andreatta C., Leonardi F. Reconocimiento de pinturas basadas en la apariencia para una guía de museo móvil // Conferencia Internacional sobre Teoría y Aplicaciones de la Visión por Computadora, VISAPP. - 2006.
[5] Leonard Wein. 2014. Reconocimiento visual en aplicaciones de guías de museos: ¿lo quieren los visitantes? .. En Actas de la Conferencia SIGCHI sobre Factores Humanos en Sistemas de Computación (CHI '14). ACM, Nueva York, NY, EE. UU., 635-638.
doi: 10.1145 / 2556288.2557270
[6] Galería Tretyakov, https://www.tretyakovgallery.ru/collection/
[7] Lukoyanov A. S., Nikolaev D. P., Konovalenko I. A. Modificación del algoritmo YAPE para imágenes con una gran extensión de contraste local // Tecnologías de la información y nanotecnologías. - 2018 .-- S. 1193-1204.
[8] Muja M., Lowe DG Búsqueda rápida de características binarias // Computer and Robot Vision (CRV), Novena conferencia de 2012 en adelante. - IEEE, 2012 .-- S. 404-410.
doi: 10.1109 / CRV.2012.60
[9] Skoryukina, N., Nikolaev, DP, Sheshkus, A., Polevoy, D. (2015, febrero). Detección de documentos rectangulares en tiempo real en dispositivos móviles. En la Séptima Conferencia Internacional sobre Visión Artificial (ICMV 2014) (Vol. 9445, p. 94452A). Sociedad Internacional de Óptica y Fotónica.
doi: 10.1117 / 12.2181377
[10] Kim A.K., Bychkov I.N. y otras tecnologías rusas "Elbrus" para computadoras personales, servidores y supercomputadoras // Tecnologías modernas de la información y educación de TI, M .: Fundación para el desarrollo de medios de Internet, educación de TI, potencial humano "League of Internet Media", 2014, No 10, p. 39-50.
[11] Kim A.K., Perekatov V.I., Ermakov S.G. Microprocesadores y sistemas informáticos.
La familia Elbrus. - San Petersburgo: Peter, 2013 .-- 272 S.