Geekly articles weekly

El cerebro desde adentro (visualización del paso del patrón a través del modelo de red neuronal artificial)

Introduccion


El artículo está dirigido a aquellos que alguna vez se hayan interesado en la cuestión de lo que está sucediendo dentro de la red neuronal artificial : el ANN . Ahora casi todos pueden desarrollar su propio ANN utilizando las bibliotecas listas para usar disponibles en la mayoría de los lenguajes de programación. En este artículo, intentaré mostrar cómo se ve exactamente el objeto ( Patrón ), pasando a través de las capas del ANN, desarrollado y compilado usando la biblioteca de aprendizaje profundo Tensorflow con el complemento Keras .

Software usado


Se requieren los siguientes componentes (las versiones que especifiqué para mi caso):

  • tensorflow 1.10.0
  • keras 2.2.4
  • matplotlib 2.2.0
  • modul-os
  • numpy1.14.3

También es posible dibujar la arquitectura de red, pero para esto es necesario instalar herramientas de visualización, en mi caso se utilizó keras y en el método

PLOT_PATTERN_PROCCESS(...)

para establecer

PLOT_MODEL = True


 def PLOT_PATTERN_PROCCESS(model, pattern, FOLDER_TO_SAVE, grid_size=(3, 3), limit_size_layer=(15, 15), PLOT_MODEL=True):

imagen

Idea principal


Es necesario elegir un patrón (el pasaje que observaremos), después de elegirlo, la red se divide en capas tensoras . En un ciclo desde la segunda hasta la última capa, se crea una nueva red, donde la salida es el número de la capa en el ciclo, y omitiendo el patrón, el resultado es una matriz n-dimensional en la salida de la red.

Implementación


Conectando bibliotecas

 from keras.models import * from keras.layers import * import matplotlib.pyplot as plt import os import numpy as np

Métodos utilizados:

  • def PLOT_PATTERN_PROCCESS (modelo, patrón, FOLDER_TO_SAVE, grid_size = (3, 3), limit_size_layer = (15, 15), PLOT_MODEL = True):
     def PLOT_PATTERN_PROCCESS(model, pattern, FOLDER_TO_SAVE, grid_size=(3, 3), limit_size_layer=(15, 15), PLOT_MODEL=True): """ :param model:   keras :type model: Sequential :param pattern:  ,       :type pattern: np.array :param FOLDER_TO_SAVE:       :type FOLDER_TO_SAVE: str :param grid_size:     :type grid_size: tuple :param limit_size_layer:      :type limit_size_layer: tuple :param PLOT_MODEL:    :type PLOT_MODEL: PLOT_MODEL """ SAVE_AR_LIST = [] for num_layer in range(1, len(model.layers)): LO = model.layers[num_layer].output _model = Model(inputs=model.input, outputs=LO) if ( len(_model.output_shape) == 3 and _model.output_shape[1] > limit_size_layer[0] and _model.output_shape[2] > limit_size_layer[1] ): _output = _model.predict(pattern)[0] SAVE_AR_LIST.append( [ num_layer, model.layers[num_layer].name, _output.tolist() ] ) ### PIC_NUM = 0 while len(SAVE_AR_LIST) > 0: fig, axs = plt.subplots(nrows=grid_size[0], ncols=grid_size[1], figsize=(10, 10), tight_layout=True) xmin, xmax = plt.xlim() ymin, ymax = plt.ylim() for ax in axs.flat: [num_layer, layer_name, ar] = SAVE_AR_LIST.pop(0) ax.imshow(np.array(ar), cmap='viridis', extent=(xmin, xmax, ymin, ymax)) ax.set_title(layer_name + " " + str(np.array(ar).shape)) if len(SAVE_AR_LIST) == 0: break # plt.show() plt.savefig(os.path.join(FOLDER_TO_SAVE, str(PIC_NUM) + '.png'), fmt='png') plt.close(fig) PIC_NUM += 1 ### if PLOT_MODEL: from keras.utils.vis_utils import plot_model plot_model( model=model, to_file=os.path.join(FOLDER_TO_SAVE, model.name + " neural network architecture.png"), show_shapes=True, show_layer_names=True ) ###

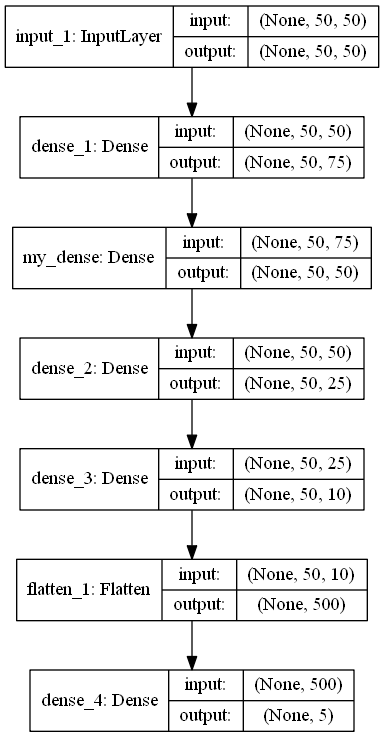
  • def build_model (IN_SHAPE = 50, CLASSES = 5) -> Secuencial:
     def build_model(IN_SHAPE=50,CLASSES=5) -> Sequential: inputs_LAYER0 = Input(shape=(IN_SHAPE,IN_SHAPE)) Dense_2_2 = Dense(75, activation='relu')(inputs_LAYER0) Dense_2_3 = Dense(50, activation='relu', name="my_dense")(Dense_2_2) Dense_2_4 = Dense(25, activation='relu')(Dense_2_3) Dense_2_5 = Dense(10, activation='relu')(Dense_2_4) flat_f_0 = Flatten()(Dense_2_5) final_layer= Dense(CLASSES, activation='softmax')(flat_f_0) # model = Model(input=inputs_LAYER0, output=final_layer, name="simple model") model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy']) model.summary() return model


Código del programa

 model_ = build_model() pattern = np.random.sample((1,50,50)) os.makedirs("PLOT_PATTERN_PROCCESS") PLOT_PATTERN_PROCCESS( model = model_, pattern = pattern, FOLDER_TO_SAVE = "PLOT_PATTERN_PROCCESS", PLOT_MODEL=False, grid_size=(2, 2) )

Descripción del programa


Método

 build_model()

devuelve un modelo ANN en formato secuencial , diseñado para clasificar algo en 5 clases.

model.summary ()
 _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= input_1 (InputLayer) (None, 50, 50) 0 _________________________________________________________________ dense_1 (Dense) (None, 50, 75) 3825 _________________________________________________________________ my_dense (Dense) (None, 50, 50) 3800 _________________________________________________________________ dense_2 (Dense) (None, 50, 25) 1275 _________________________________________________________________ dense_3 (Dense) (None, 50, 10) 260 _________________________________________________________________ flatten_1 (Flatten) (None, 500) 0 _________________________________________________________________ dense_4 (Dense) (None, 5) 2505 ================================================================= Total params: 11,665 Trainable params: 11,665 Non-trainable params: 0 _________________________________________________________________


Como puede ver en la arquitectura, un patrón es una matriz de tamaño 50x50. Variable

 pattern

y hay un objeto observable.
Luego, se crea un directorio

 os.makedirs("PLOT_PATTERN_PROCCESS")
,
donde se guardará todo el resultado.

Método Descripción PLOT_PATTERN_PROCCESS


Describí el significado del método anterior, pero es importante decir que no necesitamos todas las capas, ya que los resultados de algunas capas no se pueden mostrar o esto no será informativo.
Obtener el patrón de salida ocurre aquí:

 _output = _model.predict(pattern)[0]

En esta implementación, puede mostrar un patrón de salida bidimensional cuyas dimensiones no sean inferiores al parámetro

 limit_size_layer

Alternando a través de las capas del modelo ANN, la variable

 SAVE_AR_LIST
gradualmente lleno de datos:

  1. Número de capa

     num_layer
  2. Nombre de la capa

     model.layers[num_layer].name
  3. Salida de matriz bidimensional

      _output.tolist()

Gradualmente excluyendo un resultado de

 SAVE_AR_LIST
,
y ponerlo en la celda del lienzo

 ax.imshow(np.array(ar), cmap='viridis', extent=(xmin, xmax, ymin, ymax))
.
El resultado es un archivo (0.png)

imagen

Recomendaciones


  • Establezca el nombre de la capa de la siguiente manera:

     Dense_2_3 = Dense(50, activation='relu', name="my_dense")(Dense_2_2)

    Esto es muy conveniente al evaluar y comparar con neuroarquitectura.
  • Con este enfoque, es interesante observar cómo cambia el patrón al pasar por la red cuando se aprende de era en era
  • No instale la rejilla

     grid_size

    grande porque el tamaño de las imágenes mostradas será pequeño y poco informativo
  • Si observa el pasaje en dinámica (durante el entrenamiento o pasando un paquete de patrones), ya estamos hablando de información de tamaños grandes. Para reducir la RAM ocupada por la aplicación, es mejor guardar las matrices en archivos en una PC, por ejemplo, en formato JSON , y después de procesar todos los patrones, iterar sobre los archivos uno por uno y convertirlos en imágenes

Buena suerte

Source: https://habr.com/ru/post/438972/

More articles:


All Articles