Cómo funciona el PageRank: Implementación en R mediante álgebra lineal y el método de potencia

¡Hola, ciudadanos de Habrovsk!

Me llamo Alex Esta vez transmití desde el lugar de trabajo en ITAR-TASS.

En este breve texto, le presentaré el método de cálculo de PageRank © (en adelante, lo llamaré PR) utilizando ejemplos simples y comprensibles, en el lenguaje R. El algoritmo es una propiedad intelectual de Google, pero, debido a su utilidad para las tareas de análisis de datos, se utilizan muchas tareas. , que se puede reducir a buscar nodos grandes en el gráfico y clasificarlos por importancia.

Mencionar una gran empresa en una publicación no es un anuncio.

Como no soy un matemático profesional, utilizo, y recomiendo, este artículo y este tutorial como guía.

Comprensión intuitiva de las relaciones públicas

Comprender cómo funciona esto no es difícil. Hay un conjunto de elementos que están interconectados. Aquí está cómo están conectados exactamente: esta es una pregunta amplia: tal vez a través de enlaces (como Google), tal vez al mencionarse entre sí (casi los mismos enlaces), las probabilidades de transiciones entre elementos (matriz del proceso de Markov) pueden especificarse a priori sin especificar el físico significado de la comunicación Me gustaría asignar a estos elementos un cierto criterio de importancia, que llevaría información sobre la probabilidad de que este elemento sea visitado por alguna partícula abstracta que viaje a través del gráfico en el proceso de difusión.

Um, eso no suena muy claro. Es más fácil imaginar a un chico usando una computadora portátil con una amapola , navegando por las páginas de los resultados de búsqueda, fumando una cachimba, siguiendo enlaces de una página a otra, y cada vez aparecen más en la misma página (o páginas).

Esto se debe al hecho de que algunas páginas que visita contienen información tan interesante en la fuente original que otras páginas se ven obligadas a reimprimirla con una indicación del enlace.

Tal tipo en Google se llamaba Random surfer. Es una partícula en el proceso de difusión: un cambio discreto de posición en el gráfico a lo largo del tiempo. Y la probabilidad con la que visita la página con un tiempo de difusión que tiende al infinito es PR.

Implementación simple de cálculo de PR

Acordemos: trabajamos con 10 elementos, en un gráfico tan pequeño y acogedor.

# clear environment rm(list = ls()); gc() ## load libs library(data.table) library(magrittr) library(markovchain) ## dummy data number_nodes <- 10 node_names <- letters[seq_len(number_nodes)] set.seed(1) nodes <- sapply( seq_len(number_nodes), function(x) { paste( c( node_names[-x] , sample(node_names[-x], sample(1:5, 1), replace = T) ) , collapse = ' ' ) } ) names(nodes) <- node_names print( paste(nodes, collapse = '; ') ) ## make long dt dt <- data.table( citing_node = node_names , cited_node = nodes ) %>% .[, .(cited_node = unlist(strsplit(cited_node, ' '))), by = citing_node] %>% dcast( . , cited_node ~ citing_node , fun.aggregate = length ) dt apply(dt[,-1,with=F], 2, sum) ## affinity matrix A <- as.matrix(dt[, 2:dim(dt)[2]]) A <- sweep(A, 2, colSums(A), `/`) A[is.nan(A)] <- 0 rowSums(A) colSums(A) mark <- new("markovchain", transitionMatrix = t(A), states = node_names, name = "mark") plot(mark) 

Cada uno de los 10 elementos (nodos) contiene de 10 a 14 referencias a otros nodos en un orden aleatorio, excluyéndose a sí mismo. Por el momento, simplemente decidimos que los datos mencionados son un enlace web.

Está claro que puede suceder que algún elemento se mencione con más frecuencia que otros. Mira esto.

Por cierto, recomiendo usar el paquete data.table para experimentos. En conjunción con los principios de tidyverse, todo resulta de manera eficiente y rápida.

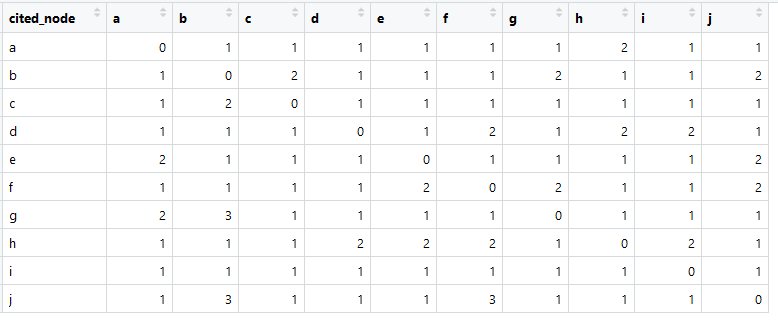
Así es como se ve nuestra matriz de enlaces (llamada en inglés con frecuencia matriz de adyacencia).

La suma en cada columna es mayor que cero, lo que significa que hay una conexión de cada elemento con algún otro elemento (esto es importante para un análisis posterior).

> aplicar (dt [, - 1, con = F], 2, suma)
abcdefghij
11 14 10 10 11 13 11 11 11 12

En base a esta tabla, podemos crear la llamada matriz de afinidad o, en nuestra opinión, la matriz de proximidad (y también se llama matriz de transición), que los matemáticos llaman matriz estocástica (matriz columna-estocástica): fuente principal

Asignarlo a una variable llamada A.



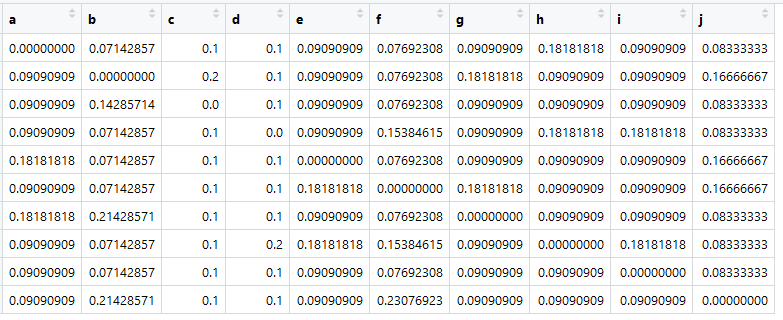
Lo más importante ahora es que la suma en todas las columnas es igual a uno.

> colSums (A)
abcdefghij
1 1 1 1 1 1 1 1 1 1

Aquí está: una matriz de transiciones, es Markov, son similitudes. Las cifras son las probabilidades de transiciones de un elemento en una columna a un elemento en una fila.

Estas, por supuesto, no son "similitudes" reales. Presente sería, por ejemplo, si calculamos el coseno del ángulo entre la presentación de documentos. Pero es importante que la matriz de transición se reduzca a (pseudo-) probabilidades para que la suma sobre cada columna sea igual a uno.

Veamos el gráfico de transición de Markov (nuestra A):



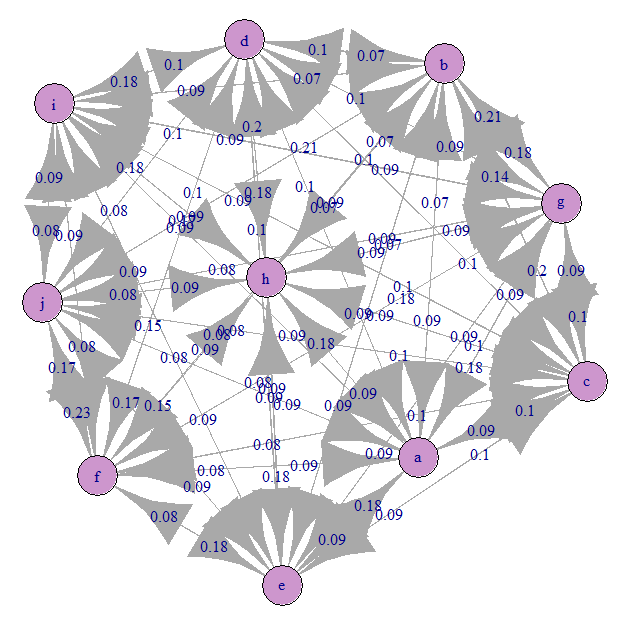
Todo está aproximadamente uniformemente confundido). Esto se debe a que especificamos transiciones equiprobables.

¡Y ahora es el momento de la magia!

 ## calculate pagerank ei <- eigen(A) as.numeric(ei$values[1]) pr <- as.numeric(ei$vectors[,1] / sum(ei$vectors[,1])) sum(pr) names(pr) <- node_names print(round(pr, 2)) 

Para una matriz estocástica A, el primer valor propio debería ser igual a la unidad, y el vector propio correspondiente es el vector PageRank.

> imprimir (redondo (pr, 2))
abcdefghij
0.09 0.11 0.09 0.10 0.10 0.11 0.10 0.11 0.08 0.11

Este es el vector de los valores de PR: este es el vector propio normalizado de la matriz de transición A correspondiente al valor propio de esta matriz igual a la unidad, el vector propio dominante.

Ahora puedes clasificar los elementos. Pero debido a los detalles del experimento, tienen un peso muy similar.

Problemas y sus soluciones usando el método de poder

La matriz de transición A puede no satisfacer las condiciones de estocasticidad.

En primer lugar, puede haber elementos que no se refieren a ninguna parte, es decir, con la ausencia de retroalimentación (pueden referirse a ellos mismos). Para gráficos reales grandes, este es un problema probable. Esto significa que una de las columnas de la matriz tendrá solo ceros. En este caso, la solución a través de vectores propios no funcionará.

Google resolvió este problema llenando una columna con una distribución de probabilidad uniforme p = 1 / N. Donde N es el número de todos los elementos.

 dim.1 <- dim(A)[1] A <- as.data.table(A) nul_cols <- apply(A, 2, function(x) sum(x) == 0) if( sum(nul_cols) > 0 ) { A[ , (colnames(A)[nul_cols]) := lapply(.SD, function(x) 1 / dim.1) , .SDcols = colnames(A)[nul_cols] ] } A <- as.matrix(A) 

En segundo lugar, el gráfico puede contener elementos que se retroalimentan entre sí, pero no los elementos restantes del gráfico. Este también es un problema insuperable para el álgebra lineal debido a la violación de supuestos.

Se resuelve introduciendo una constante llamada factor de amortiguación, que indica la probabilidad a priori de una transición de cualquier elemento a otro, incluso si no hay enlaces físicos. En otras palabras, la difusión es posible en cualquier estado.

 d = 0.15 #damping factor (to ensure algorithm convergence) M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix 

Si aplicamos estas transformaciones a nuestra matriz, ¡entonces puede resolverse nuevamente a través de vectores propios!

En tercer lugar, la matriz cursi puede no ser cuadrada, ¡pero esto es crítico! No me detendré en este momento, porque creo que tú mismo descubrirás cómo solucionarlo.

Pero hay un método más rápido y preciso, que también es más económico en la memoria (que puede ser relevante para gráficos grandes): método de potencia.

 ## pagerank function (tested on example from tutorial) rm(pagerank_func) pagerank_func <- function( A #transition matrix , eps = 0.00001 #sufficiently small error , d = 0.15 #damping factor (to ensure algorithm convergence) ) { dim.1 <- dim(A)[1] A <- as.data.table(A) nul_cols <- apply(A, 2, function(x) sum(x) == 0) if( sum(nul_cols) > 0 ) { A[ , (colnames(A)[nul_cols]) := lapply(.SD, function(x) 1 / dim.1) , .SDcols = colnames(A)[nul_cols] ] } A <- as.matrix(A) M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix rank = as.numeric(rep(1 / dim.1, dim.1)) ## iterate until convergence while( sum( (rank - M %*% rank) ^ 2 ) > eps ) { rank <- M %*% rank } return(rank) } pr2 <- pagerank_func(A) pr2=as.vector(pr2) names(pr2)=node_names 

Voila!

> imprimir (redondo (pr, 2))
abcdefghij
0.09 0.11 0.09 0.10 0.10 0.11 0.10 0.11 0.08 0.11
> imprimir (redondo (pr2, 2))
abcdefghij
0.09 0.11 0.09 0.10 0.10 0.11 0.10 0.11 0.08 0.11

Sobre esto terminaré el tutorial. Espero que les sea útil.

Olvidé decir que para construir una matriz de transiciones (probabilidades), puede usar la similitud de textos, el número de referencias, el hecho de un enlace y otras métricas que conducen a pseudo-probabilidades o son probabilidades. Un ejemplo bastante interesante es la clasificación de las oraciones en el texto en la matriz de similitud de las bolsas de palabras tf-idf para resaltar la oración que resume todo el texto. Puede haber otros usos creativos de PR.

Recomiendo probar por su cuenta para jugar con la matriz de transición y asegurarse de obtener valores PR geniales, que también son bastante fáciles de interpretar.

Si ve imprecisiones o errores conmigo, indíquelo en los comentarios o mensajes, y corregiré todo.

Todo el código se compila aquí:


PD: toda esta idea también se implementa fácilmente en otros lenguajes, al menos en Python, hice todo sin dificultad.