Métricas no triviales de la efectividad de las campañas publicitarias.

Al analizar las cadenas de canales publicitarios, algunas ideas bastante simples pero útiles pasan desapercibidas. Los analistas bien familiarizados con las matemáticas buscan sumergirse de inmediato en el aprendizaje automático, mientras que los analistas que están lejos de las matemáticas realmente no entienden dónde y cómo mirar de forma aislada de los informes estándar de Google Analytics.

Al mismo tiempo, algo tan banal como la distribución de longitudes de cadenas de atribución por un período puede decirle cosas muy elocuentes, y no solo sobre la efectividad de su publicidad.

En este artículo mostraré cómo para esta distribución:

1. Distinguir entre aquellos que pasan por canales publicitarios, aquellos usuarios que responden a la publicidad;
2. Evaluar la efectividad del impacto de su campaña publicitaria en este grupo;
3. Para evaluar cómo reaccionarían las personas a su producto si supiera todo lo que quisiera decirles;
4. Estime la frecuencia óptima de mostrar anuncios en términos de tasa de conversión.

Grupos de compromiso del usuario

Suponga que tiene datos sobre todas las cadenas de canales que los usuarios pasaron en un mes. Para comenzar, los dividiremos en dos grupos:

1. Cadenas que terminaron en conversión.
2. Cadenas que no terminaron la conversión.

Construya una tabla que contenga el número de cadenas de cierta longitud:

Longitud de la cadena	1	2	3	4 4	...
Numero de conversiones	200	400	600	1000	...
Número de conversaciones sin conversiones.	400,000	300,000	30000	7000	...

Después de eso, puede trazar el logaritmo del número de cadenas convertidas y no convertidas en su longitud y mirarlas juntas. Por ejemplo, aquí creamos un cronograma para uno de nuestros clientes B2C durante un cierto período de tiempo:


Fig.1. La dependencia del número de cadenas en la longitud de la cadena.

Cada punto del gráfico define un cierto grupo de usuarios que, durante el período considerado, completaron la conversión (línea verde) o no realizaron la conversión (línea azul) mientras completaban una cadena de una longitud determinada. Ambas gráficas bajan porque el número de cadenas disminuye exponencialmente con su longitud. Para cadenas cortas (de 2 a 7-8), el nivel de conversión (la distancia entre las líneas) aumenta gradualmente.

Hay algunos puntos extremadamente interesantes que se pueden resaltar mirando este gráfico:


Fig.2. Dependencia del número de cadenas en su longitud con regiones superpuestas que destacan varios tipos de comportamiento.

Tenemos 4 grupos de usuarios distintos:

1. Cadenas de longitud 1 y 2 (amarillo). El número de conversiones está creciendo, pero este crecimiento en sí mismo y los valores de la tasa de conversión (tasa de conversión) no corresponden a la tendencia principal. Estos son usuarios que solo están familiarizados con el producto.
2. Cadenas de longitud de 3 a 9 (verde). La tendencia principal es cuando disminuye el número de conversiones. Los gráficos son convergentes, lo que dice que la proporción de cadenas está cambiando en la dirección de aumentar la proporción de cadenas con la conversión. Es decir La tasa de conversión está aumentando. Esto es apropiado para usuarios que hacen clic específicamente en anuncios.
3. Cadenas de 9 a 15 (azul). El número de conversiones se reduce y el nivel de conversión permanece sin cambios. Los gráficos van en paralelo, lo que dice que el nivel de conversión no ha cambiado. Los usuarios tienen una idea de cómo la organización puede satisfacer sus necesidades, y la publicidad adicional no aumenta la probabilidad de una compra.
4. Mayor de 15 (rosa). Menos de 10 conversiones y conversiones sin conversiones. Muy pocos datos para decir algo.

Destacar estos 4 grupos ayuda a comprender los volúmenes de personas que potencialmente responden a la publicidad. Esto es en su mayor parte grupo (2).

Análisis de conversión grupal

Para comenzar, tira todo lo que no sea necesario. Las longitudes de más de 15 (dentro de estos datos) no son muy informativas para nosotros. Muy pocas cadenas de esta longitud no permiten ninguna conclusión. Dibujemos un gráfico del nivel de conversión versus la longitud de la cadena:


Fig.3. Tasa de conversión vs. longitud de la cadena

Este gráfico es aproximadamente con el Igmoide oh. Dichas dependencias se describen por regresión logística . La descripción de la dependencia obtenida usando la regresión logística ayuda a sacar conclusiones útiles adicionales, sin embargo, dos hechos interfieren con una buena aproximación usando la regresión logística:

• La cola inferior es demasiado baja, la regresión sobreestimará en gran medida la probabilidad de conversión para cadenas cortas.
• A medida que aumenta el número de cadenas, el gráfico no tiende a 1, como un sigmoide, sino a 0.5.

Ambos problemas se resuelven de manera bastante simple.

¿Por qué la cola inferior tiene probabilidades bajas tan inadecuadas (para la regresión logarítmica)?

Es intuitivamente obvio que si una persona hizo clic en los enlaces a su recurso al menos tres veces, probablemente no sucedió por casualidad. Y la posibilidad de una vez es muy probable. Por lo tanto, la pregunta planteada se resuelve de manera simple y radical: todas estas personas estaban en el sitio por casualidad (muy probablemente), y no necesitaban sus productos ni sus servicios. Pero aquí están en su sitio, y es probable que se conviertan.

Por lo tanto, simplemente ya no consideraremos este grupo. Para aproximar la regresión logística, consideraremos solo los grupos de usuarios (2) y (3).

¿Cómo deshacerse del hecho de que la probabilidad no tiende a 1, si en regresiones logísticas debería tender a 1?

¿Qué dan las empresas de publicidad? Permiten al cliente familiarizarse completamente con la empresa, sus servicios y comodidades. Si una persona ya ha aprendido todo sobre la compañía, ¿significa esto necesariamente que comprará algo? No Lo más probable es que haya decenas y cientos de alternativas al servicio anunciado. Es probable que una persona que ya sabe todo acerca de su servicio en particular esté familiarizada con una serie de otros servicios. Y ahora tiene suficiente información para elegir con cierta probabilidad una determinada compañía en la que ordenará algo. Y esta probabilidad es menor que 1. Aumentar el número de pases en anuncios de una cierta cantidad no tiene sentido. Por lo tanto, para que el gráfico tienda a 1, solo necesita dividir todos los valores de los niveles de conversión por el valor de probabilidad al que el gráfico tiende a aumentar el número de pases en publicidad.

Evaluación integral de la efectividad de la organización y su estrategia de marketing.

Miremos lo anterior desde el otro lado. Para cadenas suficientemente largas, el número de pases de usuario adicionales en publicidad ya no juega un papel. Algo más importa. Llamamos a esto el grado de conveniencia de la empresa como tal. Ella es constante para la organización.

Luego, la probabilidad de conversión general se divide en el producto de dos probabilidades:

$$

$$P_ {conv} (l) = P_ {marketing} (l) * P_ {firm},$$

donde $$$P_ {firma}$- una evaluación integrada de la efectividad de la organización, es decir la probabilidad de comprar algo en una organización sobre la cual ya sabe todo lo que puede y conscientemente elige entre esta organización y alternativas (los pases adicionales a través de canales publicitarios no afectarán la decisión de compra). $$$P_ {marketing} (l)$- una evaluación integrada de la efectividad de una estrategia de marketing, es decir la probabilidad de comprar algo en la organización, siempre que solo influya el marketing, y si una persona sabe todo lo que es posible, definitivamente comprará en esta organización y no considerará una alternativa. Y, por supuesto, esta probabilidad depende de la longitud de la cadena. $$$l$.

Si volvemos a la Figura 3 nuevamente, veremos que el área de influencia $$$P_ {marketing} (l)$se extiende solo al (2) grupo de usuarios. Para grupo (3) - $$$P_ {marketing} (l) = 1$, lo que significa que la probabilidad de compra es $$$P_ {firma}$. En nuestro caso, en promedio $$$P_ {firme} = 0.55$lo cual es extremadamente bueno Esta cifra dice que, teniendo todas las tarjetas en la mano, una persona elige esta organización entre todas las alternativas posibles en el 55% de los casos.

Bueno, queda por agregar que ahora tenemos una racionalización para $$$P_ {marketing} (l)$, que tiende a 1. Ahora se le puede aplicar una regresión logística simple de un factor. Haremos esto aproximando los datos normalizados por 1 dividiendo los datos por sigmoide $$$P_ {firma}$.


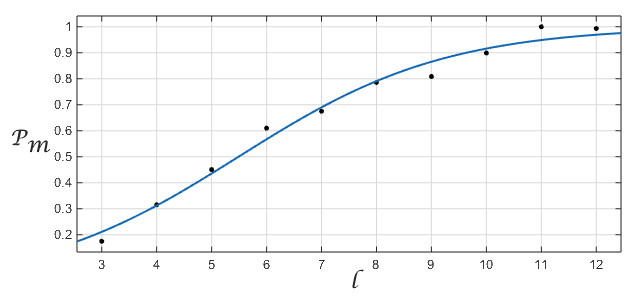Fig.4. Dependencia de la conversión en la longitud de la cadena con una curva impuesta para la regresión logística.

En la tabla $$$l$- longitud de la cadena, P _m - $$$P_ {marketing} (l)$. El exponente para el exponente es log-odds ratio = 0.53. Si una empresa tuviera un 100% de posibilidades de una "conversión consciente" ( $$$P_ {firme} = 1$), esto significaría aproximadamente que con cada aumento de la cadena en uno, la proporción del número de cadenas con y sin conversión cambiaría en [exp (0.53) = 1.699].

Este indicador mide el grado de efectividad de la estrategia de marketing en su conjunto. Cuanto más rápido se alcanza la probabilidad $$$P_ {firma}$, cuanto más efectiva sea la estrategia. Naturalmente, debes asegurarte de que $$$P_ {firma}$tomó valores satisfactorios para su negocio, de lo contrario, una estrategia de marketing efectiva obligará a un cliente potencial a comprar algo que no sea de usted.

Estimación de la frecuencia óptima de publicidad en el canal.

Considere la figura (3), que muestra la dependencia de la probabilidad de conversión del número de canales que el usuario ha recorrido actualmente. Cada punto en el gráfico corresponde a una determinada sección condicional del público objetivo. Por ejemplo, las personas que pasaron por 10 canales son algo diferentes de las que pasaron por solo 2, porque la mayoría de los que pasaron por dos canales no llegarán a 10.

Además, para aquellos que pasaron por 10 canales, los programas de marketing probablemente ya no funcionen. Ya han visto todos los anuncios posibles. Para aquellos que han pasado por solo dos canales, la publicidad puede funcionar. Por lo tanto, toda la estrategia de marketing debe centrarse específicamente en el grupo (2). Las personas que han pasado más de dos canales, pero aún no han pasado, por ejemplo, 10.

Nuestro estudio de los datos mostró que para el grupo (2) existe una correlación negativa significativa entre el nivel de conversión y el número total de clics en anuncios durante un período determinado. Es decir Mientras más personas de Asia Central, en principio, pasen por un determinado canal publicitario, menos probable será que un miembro del grupo (2) de este canal se convierta.


Fig. 5. La relación entre correlación y diferentes longitudes de cadena. La correlación es el coeficiente de correlación de Pearson entre el nivel de conversión y el número total de clics en los canales publicitarios.

Esto puede deberse al hecho de que el aumento de las conversiones está asociado con un aumento de las impresiones. Los algoritmos inteligentes de las plataformas publicitarias intentan mostrar publicidad de la parte más efectiva del público objetivo, pero esta parte es limitada. Por lo tanto, con un aumento en el número de impresiones, los algoritmos se ven obligados a comenzar a mostrar anuncios a la parte menos efectiva del público objetivo. Es menos probable que esta parte de la CA se convierta.

Se puede suponer que existe una elección óptima de la frecuencia de impresiones del anuncio en el canal, lo que afectaría solo a la parte más efectiva del público objetivo. El grado de adecuación de la elección de la frecuencia actual se puede estimar calculando la correlación entre el número total de transiciones para el período y el nivel de conversión. Si esta correlación es negativa, debe reducir la frecuencia de las impresiones. Si es aproximadamente igual a 0, entonces el tamaño es óptimo. Si es positivo, se puede aumentar el tamaño de la audiencia.

En nuestro caso, un cambio en la frecuencia de impresiones, que condujo a una disminución en el número de conversiones en un 25%, llevó a un aumento en la tasa de conversión promedio del grupo (2) de 3.5% a 4%.

Conclusiones y limitaciones.

Métricas clave sugeridas:

1. Tamaño del grupo (2). Le permite estimar cuántas personas en el período del informe reaccionaron activamente a los anuncios.
   
2. La probabilidad de la conversión de una persona que generalmente sucedió por casualidad y no necesita nada de la organización. Se estima por la tasa de conversión de las cadenas de "un paso". En el caso de los datos revisados ​​aquí, esto es 0.06%.
   
3. Dividiendo la probabilidad de conversión por dos longitudes de cadena $$$P_ {firma}$y $$$P_ {marketing}$se puede estimar:
   
   • Evaluación integral de la efectividad organizacional. Es decir La probabilidad de comprar el producto, siempre que con una visualización adicional del anuncio, la opinión de la persona sobre el producto y la empresa no cambie en absoluto. En nuestro caso, es del 55%.
     
   • Una evaluación integrada de la efectividad de una estrategia de marketing mediante el indicador de regresión logística, que puede aproximarse a la dependencia existente del nivel de conversión en la longitud de la cadena. Con cada aumento de la cadena en uno, la probabilidad de conversión aumenta y alcanzaría el 100% en algún momento si $$$P_ {firme} = 1$. El índice de regresión logística indica la gravedad de este aumento.
     
4. La correlación entre el nivel de conversión y el número total de clics grupales (2) en el canal publicitario para el período nos permite estimar la frecuencia óptima de impresiones en el canal.

Todo lo anterior tiene una serie de limitaciones en la interpretación. Y la principal limitación nos impone el tiempo final de consideración. Obviamente, las cadenas suficientemente largas aún pueden terminar con la conversión en algún momento en el futuro (que aún no hemos encontrado) y un nivel "real" de conversión de la cadena puede ser algo mayor. Es razonable suponer que Pfirm está algo subestimado y que esta evaluación es una evaluación integral de la efectividad de la organización desde abajo. Para evitar estas dificultades, podemos considerar un intervalo de tiempo en el que todos estos efectos de tiempo finito serían muy pequeños. Por ejemplo, un año entero.

PD: para estar al tanto de las noticias de Maxilect y ser el primero en conocer todas las publicaciones, suscríbase a nuestras páginas en VK , FB o Telegram-channel .