¿Cómo se organiza el código de barras?

Hola Habr!

Una persona moderna encuentra códigos de barras todos los días, sin siquiera pensarlo. Cuando compramos productos en el supermercado, sus códigos se leen precisamente con la ayuda de un código de barras. También paquetes, productos en almacenes, y así sucesivamente. Sin embargo, pocas personas saben cómo funciona realmente.

¿Cómo está organizado el código de barras y qué está codificado en esta imagen?



Intentemos resolverlo, al mismo tiempo escribiremos un decodificador de dichos códigos.

Introduccion

El uso de códigos de barras tiene una larga historia. Los primeros intentos de automatización comenzaron en la década de 1950; una patente para un lector de código se obtuvo en 1952. El ingeniero involucrado en la clasificación de los vagones en el ferrocarril quería simplificar el proceso. La idea era obvia: codificar el número con tiras y leerlas con fotocélulas. En 1962, los códigos comenzaron a usarse oficialmente para identificar autos en el ferrocarril estadounidense (sistema KarTrak ), en 1968 el reflector fue reemplazado por un rayo láser, lo que aumentó la precisión y redujo el tamaño del lector. En 1973, apareció el formato "Código de producto universal", y en 1974 el primer producto se vendió usando un escáner de código (el chicle de Wrigley es Estados Unidos) en un supermercado. En 1984, un tercio de las tiendas usaban serpentinas, pero en Rusia comenzaron a usarse alrededor de los años 90.

Se utilizan muchos códigos diferentes para diferentes tareas, por ejemplo, la secuencia "12345678" se puede representar de esta manera (y esto no es todo):



Comencemos el análisis bit a bit. Además, todo lo que se describe a continuación se referirá al formulario "Código 128", simplemente porque su formato es bastante simple y directo. Aquellos que deseen experimentar con otras especies pueden abrir un generador en línea y ver por sí mismos.

A primera vista, el código de barras parece ser solo una secuencia aleatoria de líneas, de hecho, su estructura está claramente fijada:



1 - Espacio vacío necesario para identificar claramente el inicio del código
2 - Símbolo de inicio. Para el Código 128, son posibles 3 opciones (llamadas A, B y C): 11010000100, 11010010000 o 11010011100, corresponden a diferentes tablas de códigos (más en Wikipedia ).
3 - En realidad, el código que contiene los datos que necesitamos
4 - Suma de verificación
5 - Símbolo de parada. Para el Código 128, esto es 1100011101011.
6 (1) - Espacio vacío.

Ahora sobre cómo se codifican los bits. Aquí todo es muy simple: si toma el ancho de la línea más delgada como "1", la línea de doble ancho dará el código "11", un triple "111", y así sucesivamente. El espacio vacío será "0" o "00" o "000" según el mismo principio. Aquellos que lo deseen pueden comparar el código de inicio en la imagen para asegurarse de que se cumpla la regla.

Ahora puedes comenzar a programar.

Obtenga la secuencia de bits

En principio, esta es la parte más difícil y, por supuesto, algorítmicamente, se puede implementar de diferentes maneras. No estoy seguro de que el siguiente algoritmo sea óptimo, pero es suficiente para un estudio de caso.

Para comenzar, cargue la imagen, estírela en ancho, tome una línea horizontal desde el centro de la imagen, conviértala en b / w y cárguela como una matriz.

from PIL import Image import numpy as np import matplotlib.pyplot as plt image_path = "barcode.jpg" img = Image.open(image_path) width, height = img.size basewidth = 4*width img = img.resize((basewidth, height), Image.ANTIALIAS) hor_line_bw = img.crop((0, int(height/2), basewidth, int(height/2) + 1)).convert('L') hor_data = np.asarray(hor_line_bw, dtype="int32")[0] 

En el código de barras, "1" corresponde a negro, y en RGB, por el contrario, 0, por lo que la matriz debe invertirse. Al mismo tiempo, calculamos el valor promedio.

 hor_data = 255 - hor_data avg = np.average(hor_data) plt.plot(hor_data) plt.show() 

Iniciamos el programa para asegurarnos de que el código de barras se cargue correctamente:



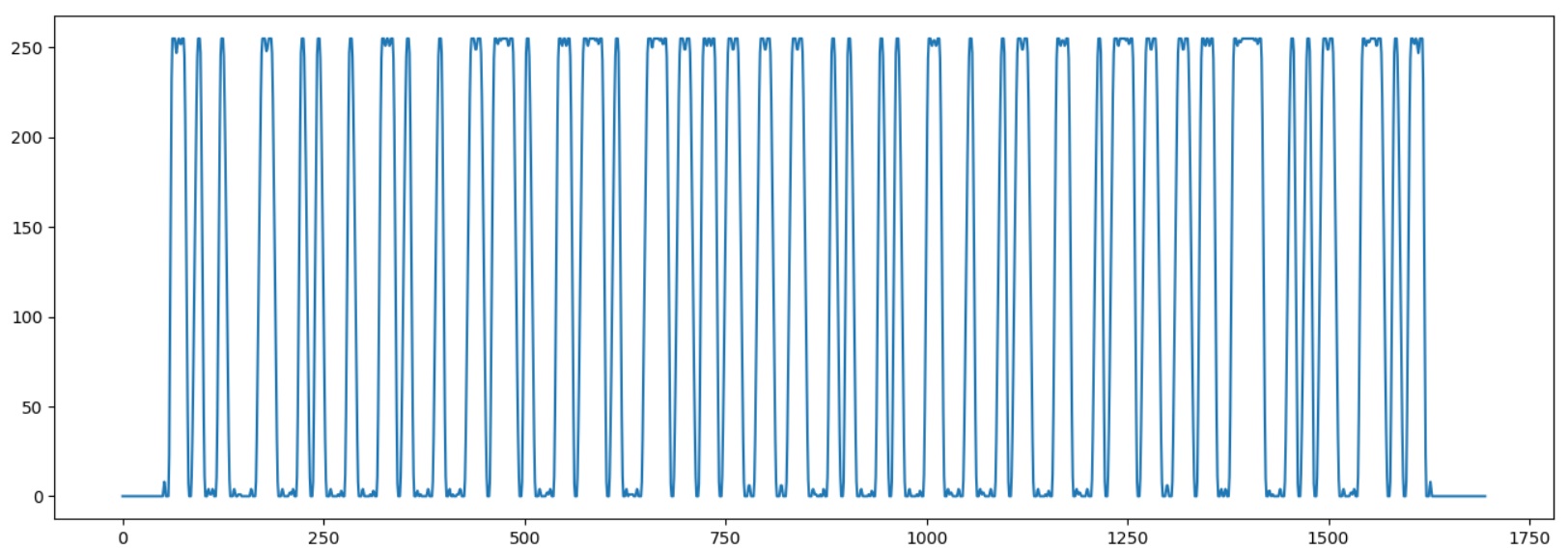
Ahora necesita determinar el ancho de un "bit". Para hacer esto, destacamos el comienzo de la secuencia de inicio "1101", registrando los momentos de transición del gráfico a través de la línea media.

 pos1, pos2 = -1, -1 bits = "" for p in range(basewidth - 2): if hor_data[p] < avg and hor_data[p + 1] > avg: bits += "1" if pos1 == -1: pos1 = p if bits == "101": pos2 = p break if hor_data[p] > avg and hor_data[p + 1] < avg: bits += "0" bit_width = int((pos2 - pos1)/3) 

Registramos solo las transiciones a través del medio, por lo que el código "1101" se escribirá como "101", pero esto es suficiente para que podamos encontrar su ancho en píxeles.

Ahora la decodificación real. Encontramos la siguiente transición a través del medio, y determinamos el número de bits que caen en el intervalo. Como la coincidencia no es absoluta (el código puede estar ligeramente curvado o estirado), utilizamos el redondeo.

 bits = "" for p in range(basewidth - 2): if hor_data[p] > avg and hor_data[p + 1] < avg: interval = p - pos1 cnt = interval/bit_width bits += "1"*int(round(cnt)) pos1 = p if hor_data[p] < avg and hor_data[p + 1] > avg: interval = p - pos1 cnt = interval/bit_width bits += "0"*int(round(cnt)) pos1 = p 

No estoy seguro de si esta es la mejor opción, tal vez hay una mejor manera, aquellos que lo deseen pueden escribir en los comentarios.

Si todo se hizo correctamente, obtenemos la siguiente secuencia de salida:

11010010000110001010001000110100010001101110100011011101000111011011
01100110011000101000101000110001000101100011000101110110011011001111
00010101100011101011

Decodificación

Aquí, en principio, no hay dificultades. Los caracteres en el Código 128 están codificados con un código de 11 bits, que tiene 3 variedades (A, B y C) y puede almacenar diferentes codificaciones de caracteres o números del 00 al 99.

En nuestro caso, el comienzo de la secuencia es 11010010000, que corresponde al "Código B". Se rompió terriblemente para manejar manualmente todos los códigos de Wikipedia, por lo que la tabla simplemente se copió del navegador y su análisis también se realizó en Python (pista: esto no es necesario para la producción).

  CODE128_CHART = """ 0 _ _ 00 32 S 11011001100 212222 1 ! ! 01 33 ! 11001101100 222122 2 " " 02 34 " 11001100110 222221 3 # # 03 35 # 10010011000 121223 ... 93 GS } 93 125 } 10100011110 111341 94 RS ~ 94 126 ~ 10001011110 131141 103 Start Start A 208 SCA 11010000100 211412 104 Start Start B 209 SCB 11010010000 211214 105 Start Start C 210 SCC 11010011100 211232 106 Stop Stop - - - 11000111010 233111""".split() SYMBOLS = [value for value in CODE128_CHART[6::8]] VALUESB = [value for value in CODE128_CHART[2::8]] CODE128B = dict(zip(SYMBOLS, VALUESB)) 

Ahora queda lo más simple. Rompemos nuestra secuencia de bits en bloques de 11 caracteres:

 sym_len = 11 symbols = [bits[i:i+sym_len] for i in range(0, len(bits), sym_len)] 

Finalmente, formamos la línea y la mostramos en la pantalla:

 str_out = "" for sym in symbols: if CODE128A[sym] == 'Start': continue if CODE128A[sym] == 'Stop': break str_out += CODE128A[sym] print(" ", sym, CODE128A[sym]) print("Str:", str_out) 

No daré la respuesta a lo que está codificado en la tabla, deje que sea una tarea para los lectores (el uso de programas listos para teléfonos inteligentes se considerará trampa :).

El código tampoco implementa la verificación CRC, quienes lo deseen pueden hacerlo ellos mismos.

Por supuesto, el algoritmo es imperfecto y se escribió en media hora. Para fines más profesionales, hay bibliotecas listas para usar , por ejemplo pyzbar . El código que usa una biblioteca de este tipo solo tomará 4 líneas:

 from pyzbar.pyzbar import decode img = Image.open(image_path) decode = decode(img) print(decode) 

(primero debe instalar la biblioteca ingresando el comando pip install pyzbar)

Adición : vinograd19 escribió en los comentarios sobre el conteo de CRC:

La historia del dígito de verificación es interesante. Surgió evolutivamente.
El dígito de verificación es necesario para evitar una decodificación incorrecta. Si el código de barras era 1234 y se reconoció como 7234, entonces necesita una validación que evitará el reemplazo de 1 por 7. La validación puede ser inexacta, de modo que al menos el 90% de los números no válidos se determinan por adelantado.

1er enfoque: tomemos la cantidad. Para que el resto de la división entre 10 sea 0. Bueno, es decir, los primeros 12 caracteres llevan una carga de información, y el último dígito se selecciona de modo que la suma de los dígitos se divida por 10. Decodifique la secuencia, si la suma no es divisible por diez, significa decodificado con un error y debe hacerlo Esta vez más. Por ejemplo, el código 1234 es válido. 1 + 2 + 3 + 4 = 10. El código 1216 también es válido, pero 1218 no lo es.

Esto evita problemas con la automatización. Sin embargo, en el momento de crear los códigos de barras, hubo un retroceso en la forma de escribir un número en las teclas. Y hay un mal caso: si cambia el orden de los dos dígitos, la suma de verificación no cambia, y esto es malo. Es decir, si el código de barras 1234 se introdujo como 2134, la suma de verificación convergerá, pero ingresamos el número incorrecto. Resulta que el orden incorrecto de los números es un caso común si toca las teclas rápidamente.

2º enfoque Bueno, hagamos que la cantidad sea un poco más complicada. Para que los números en lugares pares se tengan en cuenta dos veces. Luego, al cambiar el orden, la cantidad definitivamente no convergerá al deseado. Por ejemplo, el código 2364 es válido (2 + 3 + 3 + 6 + 4 + 4 = 20), y el código 3264 no es válido (3+ 2 + 2 + 6 + 4 + 4 = 19). Pero aquí había otro mal ejemplo de conducción. Algunos teclados son tales que diez dígitos están dispuestos en dos filas. la primera fila es 12345 y debajo de la segunda segunda fila es 67890. Si, en lugar de la tecla "1", presione la tecla "2" a la derecha, la suma de verificación evitará la entrada incorrecta. Pero si en lugar de la tecla "1", presiona la tecla "6" a continuación, es posible que no advierta. Después de todo, 6 = 1 + 5, y en el caso de que esta cifra esté en un lugar par al calcular la suma de verificación, tenemos 2 * 6 = 2 * 1 + 2 * 5. Es decir, la suma de verificación aumentó exactamente 10, por lo que su último dígito no ha cambiado. Por ejemplo, las sumas de verificación en los códigos 2134 y 2634 son las mismas. El mismo error ocurrirá si presionamos 7 en lugar de 2, en lugar de 3 presionamos 8, y así sucesivamente.

3er enfoque. Ok, tomemos la suma nuevamente, solo se tendrán en cuenta los números en lugares pares ... tres veces. Es decir, el código 1234565 es válido, porque 1 + 2 * 3 + 3 + 4 * 3 + 5 + 6 * 3 +5 = 50.

El método descrito se ha convertido en el estándar para calcular la suma de verificación EAN13 con algunas correcciones: el número de dígitos se ha vuelto fijo e igual a 13, donde el 13 es la misma suma de verificación. Los números en lugares impares se cuentan tres veces, en pares, una vez.

Conclusión

Como puede ver, incluso algo tan simple como un código de barras tiene muchas cosas interesantes. Por cierto, otro truco de vida para aquellos que han leído hasta aquí: el texto debajo del código de barras (si lo hay) duplica completamente su contenido. Esto se hace para que, en caso de código ilegible, el operador pueda ingresarlo manualmente. Por lo tanto, averiguar el contenido de un código de barras suele ser simple: solo mire el texto debajo de él.

Como se sugiere en los comentarios, el más popular en el comercio es el código EAN-13, la codificación de bits es la misma allí, y aquellos que lo deseen pueden ver la estructura de los personajes.

Si los lectores no han perdido interés, puede considerar por separado los códigos QR.

Gracias por su atencion