Aprendizaje profundo de refuerzo: ping pong de píxel sin procesar

Este es un artículo muy retrasado sobre el aprendizaje por refuerzo (RL). ¡RL es un tema genial!

Es posible que sepa que las computadoras ahora pueden aprender automáticamente a jugar juegos ATARI (¡obteniendo píxeles de juego en bruto en la entrada!). Vencieron a los campeones del mundo en el juego de Go , los cuatro patas virtuales aprenden a correr y saltar , y los robots aprenden a realizar tareas complejas de manipulación que desafían la programación explícita. Resulta que todos estos logros no están completos sin RL. También estuve interesado en RL durante el año pasado: trabajé con el libro de Richard Sutton (aprox. Referencia: reemplazado) , leí el curso de David Silver , asistí a las conferencias de John Schulman , escribí la biblioteca de RL en Javascript e hice prácticas en DeepMind en el verano, trabajando en un grupo DeepRL, y más recientemente, en el desarrollo de OpenAI Gym , es el nuevo kit de herramientas RL. Así que, por supuesto, he estado en esta ola durante al menos un año, pero aún no me he molestado en escribir una nota sobre por qué RL es de gran importancia, de qué se trata, cómo se desarrolla todo.


Ejemplos de uso de Deep Q-Learning. De izquierda a derecha: la red neuronal juega ATARI, la red neuronal juega AlphaGo, el robot pliega Lego, las carreras virtuales de cuatro patas alrededor de obstáculos virtuales.

Es interesante reflexionar sobre la naturaleza del progreso reciente en RL. Me gustaría señalar cuatro factores separados que afectan el desarrollo de la IA:

1. Velocidad de cómputo (GPU, dispositivos especiales ASIC, ley de Moore)
2. Datos suficientes en forma utilizable (por ejemplo, ImageNet)
3. Algoritmos (investigación e ideas, por ejemplo, backprop, CNN, LSTM)
4. Infraestructura (Linux, TCP / IP, Git, ROS, PR2, AWS, AMT, TensorFlow, etc.).

Al igual que en la visión por computadora, el progreso en RL se está moviendo ... aunque no tanto como podría parecer. Por ejemplo, en visión artificial, la red neuronal AlexNet 2012 es una versión aumentada en profundidad y anchura de la red neuronal ConvNets de los años noventa. Del mismo modo, ATARI Deep Q-Learning 2013 es una implementación del algoritmo estándar Q-Learning que puedes encontrar en el libro clásico de Richard Sutton de 1998. Además, AlphaGo utiliza la técnica Policy Gradient y la búsqueda de árbol de Monte Carlo (MCTS) también son ideas antiguas o sus combinaciones. Por supuesto, se necesitan muchas habilidades y paciencia para que funcionen, y se han desarrollado muchas configuraciones difíciles sobre algoritmos antiguos. Pero en una primera aproximación, el principal impulsor del progreso reciente no son los nuevos algoritmos e ideas, sino la intensificación de los cálculos, los datos suficientes y la infraestructura madura.

Ahora de vuelta a RL. Muchas personas no pueden creer que podemos enseñarle a una computadora cómo jugar juegos ATARI a nivel humano usando píxeles sin formato desde cero y usando el mismo algoritmo de autoaprendizaje. Al mismo tiempo, cada vez que siento una brecha: lo mágico que parece y lo simple que realmente es por dentro.

El enfoque básico que utilizamos es bastante tonto. Sea como fuere, me gustaría presentarles la técnica de Gradiente de Política (PG), nuestra opción predeterminada favorita para resolver problemas con RL en este momento. Puede que tenga curiosidad por qué, en cambio, no puedo imaginar DQN, que es un algoritmo RL alternativo y mejor conocido que también se usa en el entrenamiento ATARI . Resulta que aunque Q-Learning es conocido, no es tan perfecto. La mayoría de las personas optan por usar Policy Gradient, incluidos los autores del artículo original de DQN , que han demostrado que con un buen ajuste, Policy Gradient funciona incluso mejor que Q-Learning. PG es preferible porque es explícito: hay una política clara y un enfoque coherente que optimiza directamente las recompensas esperadas. Como ejemplo, aprenderemos a jugar ATARI Pong: desde cero, desde píxeles sin procesar a través de un Gradiente de política con una red neuronal. Y pondremos todo esto en 130 líneas de Python. ( Enlace general ) Veamos cómo se hace esto.



Arriba: Ping Pong. A continuación: Presentación de ping-pong como un caso especial del proceso de toma de decisiones de Markov (MDP) : cada vértice del gráfico corresponde a un cierto estado del juego, y los bordes determinan las probabilidades de transición a otros estados. Cada costilla también determina la recompensa. El objetivo es encontrar el mejor camino desde cualquier estado para maximizar la recompensa

Jugar Ping Pong es un gran ejemplo de un desafío RL. En la versión ATARI 2600 jugaremos una raqueta nosotros mismos. Otra raqueta está controlada por un algoritmo incorporado. Necesitamos golpear la pelota para que el otro jugador no tenga tiempo de golpearla. Espero que no haya necesidad de explicar qué es Ping Pong. En un nivel bajo, el juego funciona de la siguiente manera: obtenemos un marco de imagen, una matriz de bytes 210x160x3, y decidimos si queremos mover la raqueta ARRIBA o ABAJO. Es decir, solo tenemos dos opciones para administrar el juego. Después de cada elección, el simulador de juego realiza su acción y nos da una recompensa: ya sea +1 recompensa si la pelota pasó la raqueta del oponente, o -1 si la perdimos. De lo contrario, 0. Y, por supuesto, nuestro objetivo es mover la raqueta para que obtengamos la mayor recompensa posible.

Al considerar una solución, recuerde que intentaremos hacer tan pocos supuestos sobre el pong, porque no es particularmente importante en la práctica. Tenemos mucho más en cuenta en las tareas a gran escala, como la manipulación de robots, el ensamblaje y la navegación. Pong es solo un divertido caso de prueba de juguete con el que jugamos mientras descubrimos cómo escribir sistemas de IA muy generales que algún día puedan realizar tareas útiles arbitrarias.

Red neuronal como una política RL . En primer lugar, vamos a determinar la llamada política que implementa nuestro jugador (o "agente"). ((*) "Agente", "medio ambiente" y "política de agente" son términos estándar de la teoría RL). La función política en nuestro caso es una red neuronal. Ella aceptará el estado del juego en la entrada y en la salida decidirá qué hacer: moverse hacia arriba o hacia abajo. Como nuestro bloque de cálculos simple favorito, utilizaremos una red neuronal de dos capas que toma píxeles de imagen sin procesar (un total de 100.800 números (210 * 160 * 3)) y produce un solo número que indica la probabilidad de mover la raqueta hacia arriba. Tenga en cuenta que el uso de la política estocástica es estándar, lo que significa que solo producimos la probabilidad de un movimiento ascendente. Para obtener el movimiento real, utilizaremos esta probabilidad. La razón de esto se aclarará cuando hablemos de capacitación.


Nuestra función política consiste en una red neuronal completamente conectada de 2 capas

Más específicamente, suponga que en la entrada obtenemos un vector X, que contiene un conjunto de píxeles preprocesados. Luego debemos calcular usando python \ numpy:

h = np.dot(W1, x) # compute hidden layer neuron activations h[h<0] = 0 # ReLU nonlinearity: threshold at zero logp = np.dot(W2, h) # compute log probability of going up p = 1.0 / (1.0 + np.exp(-logp)) # sigmoid function (gives probability of going up) 

En este fragmento, W1 y W2 son dos matrices que inicializamos al azar. No usamos sesgos, porque queríamos hacerlo. Tenga en cuenta que al final usamos la no linealidad del sigmoide, lo que reduce la probabilidad de salida al rango [0,1]. Intuitivamente, las neuronas en una capa oculta (cuyos pesos se encuentran en W1) pueden detectar varios escenarios de juego (por ejemplo, la pelota está en la parte superior y nuestra raqueta en el medio), y los pesos en W2 pueden decidir si debemos subir en cada caso o abajo. Los primeros W1 y W2 aleatorios, por supuesto, al principio causarán espasmos y convulsiones en nuestro neuro-jugador, lo que lo equipara a un autista imbécil a los mandos de un avión. Entonces, la única tarea ahora es encontrar W1 y W2, ¡lo que conduce a un buen juego!

Hay una observación sobre el preprocesamiento de píxeles: idealmente, debe transferir al menos 2 fotogramas a la red neuronal para que pueda detectar el movimiento. Pero para simplificar la situación, aplicaremos la diferencia de dos cuadros. Es decir, restaremos los cuadros actuales y anteriores y solo entonces aplicaremos la diferencia a la entrada de la red neuronal.

Suena como algo imposible. En este punto, me gustaría que aprecie lo complejo que es el problema de RL. Obtenemos 100 800 números (210x160x 3) y lo enviamos a nuestra red neuronal que implementa la política del jugador (que, por cierto, incluye fácilmente alrededor de un millón de parámetros en las matrices W1 y W2). Supongamos que en algún momento decidimos subir. El simulador de juego puede responder que esta vez obtendremos 0 premios y nos dará otros 100 800 números para el próximo cuadro. ¡Podemos repetir este proceso cientos de veces antes de obtener una recompensa distinta de cero! Por ejemplo, supongamos que finalmente tenemos una recompensa +1. Esto es maravilloso, pero ¿cómo podemos decir, qué nos llevó a esto? ¿Fue esta la acción que hicimos ahora? O tal vez 76 cuadros de vuelta? ¿O tal vez esto se asoció primero con el cuadro 10, y luego hicimos algo bien en el cuadro 90? ¿Y cómo descubrimos cuál de los millones de "bolígrafos" para torcer para lograr un éxito aún mayor en el futuro? Llamamos a esto la tarea de determinar el coeficiente de confianza en ciertas acciones. En el caso específico con el pong, sabemos que obtenemos +1 si la pelota pasa al oponente. La verdadera razón es que accidentalmente pateamos la pelota a lo largo de un buen camino unos pocos cuadros hacia atrás, y cada acción posterior que realizamos no la afectó en absoluto. En otras palabras, nos enfrentamos a un problema computacional muy complejo, y todo parece bastante sombrío.

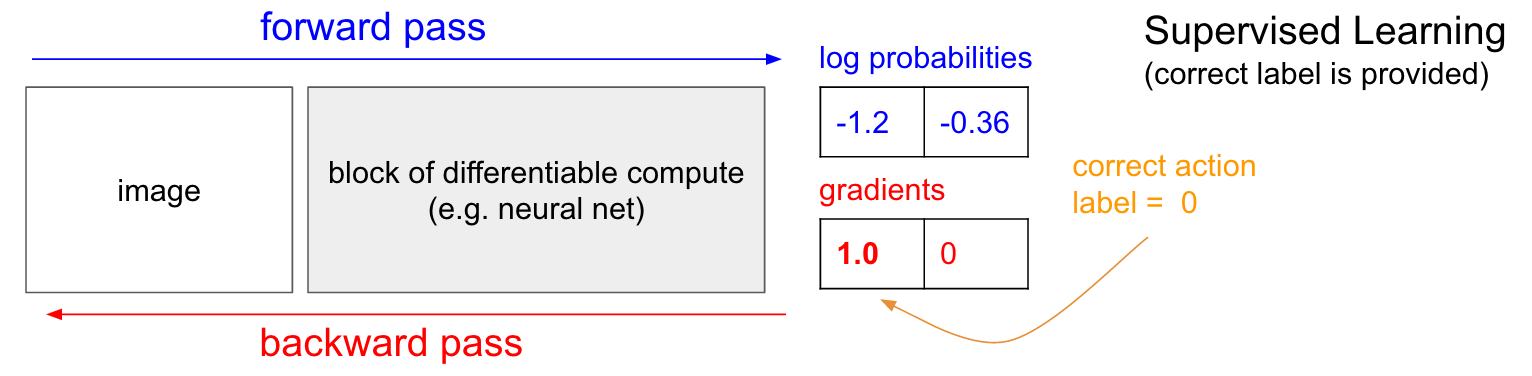
Entrenamiento con un profesor. Antes de profundizar en el gradiente de la política (PG), me gustaría recordar brevemente la enseñanza con un maestro, porque, como veremos, RL es muy similar. Consulte la tabla a continuación. En la enseñanza ordinaria con un maestro, transferiremos la imagen a la red y recibiremos en la salida algunas probabilidades numéricas para las clases. Por ejemplo, en nuestro caso tenemos dos clases: ARRIBA y ABAJO. Utilizo las probabilidades logarítmicas (-1.2, -0.36) en lugar de las probabilidades en el formato 30% y 70%, porque optimizamos la probabilidad logarítmica de la clase (o etiqueta) correcta. Esto hace que los cálculos matemáticos sean más elegantes y equivale a optimizar solo la probabilidad, porque el logaritmo es monótono.

En el entrenamiento con un maestro, tendremos acceso instantáneo a la clase correcta (etiqueta). En la etapa de entrenamiento, nos dirán exactamente qué paso correcto se necesita en este momento (digamos que es ARRIBA, etiqueta 0), aunque la red neuronal puede pensar de manera diferente. Por lo tanto, calculamos el gradiente $$$\ nabla_ {W} \ log p (y = UP \ mid x)$ para ajustar la configuración de red. Este gradiente solo nos dice cómo deberíamos cambiar cada uno de nuestros millones de parámetros para que la red sea un poco más probable que prediga UP en la misma situación. Por ejemplo, uno de un millón de parámetros en la red puede tener un gradiente de -2.1, lo que significa que si aumentamos este parámetro en un valor positivo pequeño (por ejemplo, 0.001), la probabilidad logarítmica de UP disminuirá en 2.1 * 0.001. (disminución debido al signo negativo). Si aplicamos el gradiente y luego actualizamos el parámetro usando el algoritmo de retropropagación, entonces, sí, nuestra red dará una alta probabilidad de UP cuando vea la misma imagen o una muy similar en el futuro.



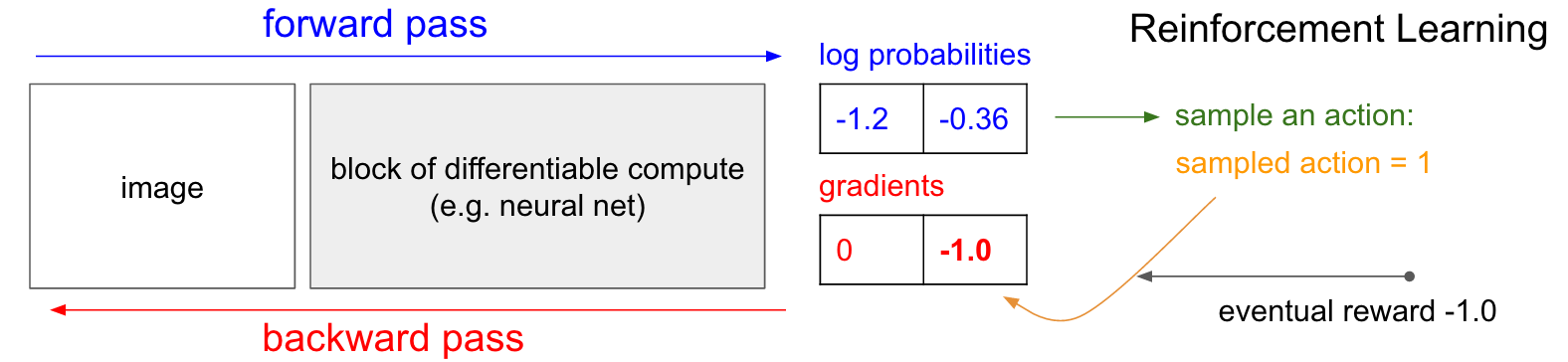
Gradientes de Política (PG) . Bien, pero ¿qué hacemos si no tenemos la etiqueta de entrenamiento de refuerzo correcta? Aquí hay una solución para PG (consulte el diagrama a continuación nuevamente). Nuestra red neuronal calculó la probabilidad de un aumento del 30% (logprob -1.2) y DOWN en un 70% (logprob -0.36). Ahora hacemos una selección de esta distribución y especificamos qué acción haremos. Por ejemplo, eligieron ABAJO y enviaron esta acción al simulador de juego. En este punto, preste atención a un hecho interesante: podríamos calcular inmediatamente y aplicar el gradiente para la acción DOWN, como lo hicimos al enseñar con un maestro, y así hacer que la red sea más propensa a realizar la acción DOWN en el futuro. Por lo tanto, podemos apreciar y recordar de inmediato este gradiente. Pero el problema es que por el momento aún no lo sabemos, ¿es bueno bajar? ¡Pero lo más interesante es que podemos esperar un poco y aplicar el gradiente más tarde! En Pong, podemos esperar hasta el final del juego, luego tomar la recompensa que recibimos (ya sea +1 si ganamos o -1 si perdimos) e ingresarla como un factor para el gradiente. Entonces, si introducimos -1 para la probabilidad DOWN y hacemos la propagación hacia atrás, reconstruiremos los parámetros de la red para que sea menos probable que realice la acción DOWN en el futuro cuando encuentre la misma imagen, ya que la adopción de esta acción nos llevó a perder el juego. Es decir, tendremos que recordar de alguna manera todas las acciones (entradas y salidas de la red neuronal) en un episodio del juego y, en base a esta matriz, torcer la red neuronal casi de la misma manera que en la enseñanza con un maestro.



Y eso es todo lo que se necesita: tenemos una política estocástica que elige acciones, y luego, en el futuro, se alientan las acciones que finalmente conducen a buenos resultados, y no se alientan las acciones que conducen a malos resultados. Además, la recompensa ni siquiera debería ser +1 o -1 si finalmente ganamos el juego. Puede ser un valor arbitrario del mismo significado. Por ejemplo, si todo funciona muy bien, entonces la recompensa podría ser 10.0, que luego usaremos como un gradiente para comenzar la propagación hacia atrás. Esta es la belleza de las redes neuronales. Usarlos puede parecer un engaño: se le permite tener 1 millón de parámetros integrados en 1 teraflop de cálculos, y puede hacer que el programa aprenda a hacer cosas arbitrarias con descenso de gradiente estocástico (SGD). No debería funcionar, pero es curioso que vivamos en un universo donde funciona.

Si jugáramos juegos de mesa simples, como las damas, el orden sería aproximadamente el mismo. Hay una notable diferencia con los algoritmos de recorte minimax o alfa-beta. En estos algoritmos, el programa mira unos pasos más adelante, conoce las reglas del juego y analiza millones de posiciones. En el enfoque RL, solo se analizan los movimientos realizados. Al mismo tiempo, la red neuronal no mira hacia adelante, ya que no sabe nada sobre las reglas del juego.

Orden de entrenamiento en detalle. Creamos e inicializamos una red neuronal con algunos W1, W2 y jugamos 100 juegos de pong (lo llamamos el "encuentro" de la política, despliegues de políticas). Supongamos que cada juego consta de 200 cuadros, por lo que en total tomamos 100 * 200 = 20,000 decisiones de subir o bajar. Y para cada una de las soluciones, conocemos un gradiente que nos dice cómo deberían cambiar los parámetros si queremos fomentar o prohibir esta solución en este estado en el futuro. Todo lo que queda ahora es etiquetar cada decisión que tomamos como buena o mala. Por ejemplo, supongamos que ganamos 12 juegos y perdimos 88. Tomaremos todas las decisiones 200 * 12 = 2400 que tomamos en los juegos ganadores y realizaremos una actualización positiva (completando un gradiente de +1.0 para cada acción, realizando backprop y actualizando los parámetros alentando las acciones que hemos elegido en todas estas condiciones). Y tomaremos las otras 200 * 88 = 17,600 decisiones que tomamos al perder juegos y realizaremos una actualización negativa (sin aprobar lo que hicimos). Y eso es todo lo que se necesita. Ahora será más probable que la red repita acciones que han funcionado, y un poco menos probable que repita acciones que no han funcionado. Ahora jugamos otros 100 juegos con nuestra nueva política ligeramente mejorada y luego repetimos la aplicación de gradientes.


Esquema de dibujos animados de 4 juegos. Cada círculo negro es un tipo de estado del juego (a continuación se muestran tres ejemplos de estados), y cada flecha es una transición marcada con la acción que se seleccionó. En este caso, ganamos 2 juegos y perdimos 2 juegos. Tomamos los dos juegos que ganamos y alentamos ligeramente cada acción que hicimos en este episodio. Por el contrario, también tomaremos los dos juegos perdidos y desalentaremos ligeramente cada acción individual que hicimos en este episodio.

Si reflexiona sobre esto, comenzará a encontrar algunas propiedades divertidas. Por ejemplo, ¿qué pasa si hicimos una buena acción en el cuadro 50, pateando la pelota correctamente, pero luego fallamos la pelota en el cuadro 150? Desde que perdimos el juego, cada acción individual ahora está marcada como mala, ¿y esto no evita el golpe correcto en el cuadro 50? Tienes razón, así será para esta fiesta. Sin embargo, cuando considera el proceso en miles / millones de juegos, la ejecución correcta del rebote aumenta su probabilidad de ganar en el futuro. En promedio, verá más actualizaciones positivas que negativas para un ataque de raqueta adecuado. Y la política de implementación de la red neuronal finalmente producirá las reacciones correctas.

Actualización: 9 de diciembre de 2016 es una vista alternativa. En mi explicación anterior, utilizo términos como "definir un gradiente y propagación hacia atrás", que es una técnica hábil definitiva. Si está acostumbrado a escribir su propio código de propagación de backprop o usar Torch, puede controlar completamente los gradientes. Sin embargo, si está acostumbrado a Theano o TensorFlow, quedará un poco desconcertado porque el código de backprop es completamente automático y difícil de personalizar. En este caso, la siguiente vista alternativa puede ser más productiva. En la enseñanza con un maestro, el objetivo habitual es maximizar $$$\ sum_i \ log p (y_i \ mid x_i)$ donde $$$x_i, y_i$ - ejemplos de capacitación (como imágenes y sus etiquetas). La aplicación del gradiente a la función de política coincide exactamente con la capacitación con el maestro, pero con dos pequeñas diferencias: 1) no tenemos las etiquetas correctas $$$y_i$ , por lo tanto, como una "etiqueta falsa" utilizamos la acción que recibimos para seleccionar de la política cuando vio $$$x_i$ , y 2) Introducimos otro coeficiente de conveniencia (ventaja) para cada acción. Por lo tanto, al final, nuestra pérdida ahora parece $$$\ sum_i A_i \ log p (y_i \ mid x_i)$ donde $$$y_i$ - esta es la acción que llevamos a cabo con la muestra, y $$$A_i$ Es el número que llamamos coeficiente de conveniencia. Por ejemplo, en el caso de pong, el valor $$$A_i$ podría ser 1.0 si terminamos ganando el episodio, y -1.0 si perdemos. Esto garantiza que maximicemos la probabilidad de registrar acciones que condujeron a un buen resultado, y minimizar la probabilidad de registrar acciones que no lo hicieron. Y las acciones neutrales como resultado de muchas llamadas no afectarán particularmente la función de la política. Por lo tanto, el aprendizaje de refuerzo es exactamente lo mismo que aprender con un maestro, pero en un conjunto de datos (episodios) en constante cambio, con un factor adicional.

Funciones de viabilidad más avanzadas. También prometí un poco más de información. Hasta ahora, hemos evaluado la corrección de cada acción individual en función de si ganamos o no. En una configuración RL más general, recibiremos una "recompensa condicional" $$$r_t$ para cada paso, dependiendo del número de paso o el tiempo. Una de las opciones comunes es usar un coeficiente con descuento, por lo que la "recompensa posible" en el diagrama anterior será $$$R_t = \ sum_ {k = 0} ^ {\ infty} \ gamma ^ k r_ {t + k}$ donde $$$\ gamma$ Es un número del 0 al 1, llamado coeficiente de descuento (por ejemplo, 0,99). La expresión dice que la fuerza con la que fomentamos la acción es la suma ponderada de todas las recompensas, pero las recompensas posteriores son exponencialmente menos importantes. Es decir, se alientan mejor las cadenas cortas de acciones, y la cola de las largas cadenas de acciones se vuelve menos importante. En la práctica, también necesitas normalizarlos. Por ejemplo, supongamos que calculamos $$$R_t$ por todas las 20,000 acciones en una serie de 100 episodios del juego. Una muy buena idea es normalizar estos valores (restar el promedio, dividir por la desviación estándar) antes de conectarlos al algoritmo de backprop. Por lo tanto, siempre alentamos y desalentamos aproximadamente la mitad de las acciones realizadas. Esto reduce las fluctuaciones y hace que la política sea más convergente. Se puede encontrar un estudio más profundo en [ link ].

Derivado de una función política. También quería describir brevemente cómo se toman matemáticamente los gradientes. Los gradientes de la función de la política son un caso especial de una teoría más general. El caso general es que cuando tenemos una expresión de la forma $$$E_ {x \ sim p (x \ mid \ theta)} [f (x)]$ , es decir, la expectativa de alguna función escalar $$$f (x)$ con alguna distribución de su parámetro $$$p (x; \ theta)$ parametrizado por algún vector $$$\ theta$ . Entonces $$$f (x)$ se convertirá en nuestra función de recompensa (o la función de conveniencia en un sentido más general) y la distribución discreta $$$p (x)$ será nuestra política, que en realidad tiene la forma $$$p (a \ mid I)$ dando las probabilidades de una acción a para la imagen $$$I$ . Entonces estamos interesados ​​en cómo podemos cambiar la distribución de p a través de sus parámetros $$$\ theta$ para ampliar $$$f$ (es decir, cómo cambiamos la configuración de la red para que las acciones obtengan una mayor recompensa). Tenemos esto:
$$$\ begin {align} \ nabla _ {\ theta} E_x [f (x)] & = \ nabla _ {\ theta} \ sum_x p (x) f (x) & \ text {definición de expectativa} \\ & = \ sum_x \ nabla _ {\ theta} p (x) f (x) & \ text {intercambie la suma y el gradiente} \\ & = \ sum_x p (x) \ frac {\ nabla _ {\ theta} p (x)} {p (x)} f (x) & \ text {multiplicar y dividir por} p (x) \\ & = \ sum_x p (x) \ nabla _ {\ theta} \ log p (x) f (x) & \ text {use el hecho de que} \ nabla _ {\ theta} \ log (z) = \ frac {1} {z} \ nabla _ {\ theta} z \\ & = E_x [f (x) \ nabla _ {\ theta} \ log p (x)] & \ text {definición de expectativa} \ end {align}$

Trataré de explicar esto. Tenemos alguna distribución $$$p (x; \ theta)$ (Usé la abreviatura $$$p (x)$ de donde podemos seleccionar valores específicos. Por ejemplo, puede ser una distribución gaussiana de la cual un generador de números aleatorios muestrea. Para cada ejemplo, también podemos calcular la función de estimación $$$f$ , que según el ejemplo actual nos da una estimación escalar. La ecuación resultante nos dice cómo debemos cambiar la distribución a través de sus parámetros. $$$\ theta$ si queremos más ejemplos de acciones basadas en él para obtener tasas más altas $$$f$ . Tomamos algunos ejemplos de acciones. $$$x$ y su evaluación $$$f (x)$ , y también para cada x también evaluamos el segundo término $$$\ nabla _ {\ theta} \ log p (x; \ theta)$ . ¿Qué es este multiplicador? Este es precisamente el vector: el gradiente, que nos da dirección en el espacio de parámetros, lo que conducirá a un aumento en la probabilidad de una acción específica $$$x$ . En otras palabras, si empujamos θ en la dirección $$$\ nabla _ {\ theta} \ log p (x; \ theta)$ , veríamos que la nueva probabilidad de esta acción aumentará ligeramente. Si miras hacia atrás a la fórmula, nos dice que debemos tomar esta dirección y multiplicar el valor escalar por ella. $$$f (x)$ . Esto asegurará que los ejemplos de acciones con una calificación más alta (en nuestro caso, una recompensa) se “arrastren” más fuertemente que los ejemplos con un indicador más bajo, por lo tanto, si tuviéramos que actualizar en base a varias muestras de $$$p$ , la densidad de probabilidad cambiaría a la dirección de los puntos de juego más altos, lo que aumenta la probabilidad de obtener ejemplos de acciones con altas recompensas. Es importante que el gradiente no se tome de la función $$$f$ , ya que generalmente puede ser indiferenciado e impredecible. Un $$$p$ diferenciable por $$$\ theta$ . Eso es $$$p$ es una distribución discreta continuamente ajustable, donde puede ajustar las probabilidades de acciones individuales. También asumimos que $$$p$ normalizado



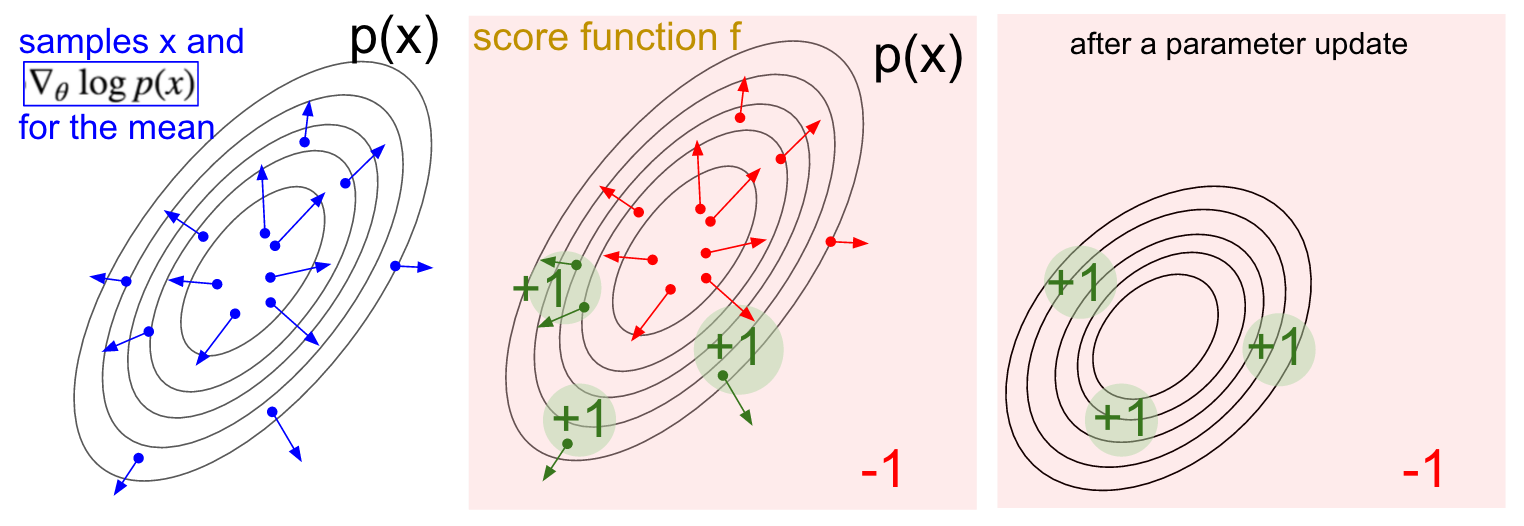Visualización de gradiente. Izquierda: distribución gaussiana y varios ejemplos de ella (puntos azules). En cada punto azul, también graficamos el gradiente de la probabilidad logarítmica con respecto al parámetro promedio. La flecha indica la dirección en la que se debe cambiar el valor de distribución promedio para aumentar la probabilidad de esta acción de ejemplo. En el medio: se agregó alguna función de evaluación que proporciona -1 en todas partes excepto +1 en algunas regiones pequeñas (tenga en cuenta que esta puede ser una función escalar arbitraria y no necesariamente diferenciable). Las flechas ahora están codificadas por colores, porque debido a la multiplicación vamos a promediar todas las flechas verdes con una calificación positiva y las flechas rojas negativas. Derecha: después de actualizar los parámetros, las flechas verdes y las flechas rojas invertidas nos empujan hacia la izquierda y hacia abajo. Las muestras de esta distribución ahora tendrán una calificación esperada más alta, si se desea.

Espero que la conexión con RL sea clara.Nuestra política nos da ejemplos de acciones, y algunas de ellas funcionan mejor que otras (a juzgar por la función de conveniencia). La forma de cambiar la configuración de la política es ejecutar, tomar el gradiente de las acciones seleccionadas, multiplicarlo por la calificación y agregar todo lo que hicimos anteriormente. Para una conclusión más completa, recomiendo una conferencia de John Shulman.

Entrenamiento Bueno, hemos desarrollado los principios de gradientes de la función de la política. Implementé todo el enfoque en un script Python de 130 líneas que usa el emulador ATAI 2600 Pong ya preparado de OpenAI Gym. Entrené una red neuronal de dos capas con 200 neuronas de capa oculta usando el algoritmo RMSProp para una serie de 10 episodios (cada episodio, de acuerdo con las reglas, consiste en varios sorteos y el episodio continúa marcando 21). No configuré demasiado los hiperparámetros y experimenté en mi Macbook lenta, pero después de un entrenamiento de tres días obtuve una política que juega un poco mejor que el reproductor incorporado. El número total de episodios fue de aproximadamente 8,000, por lo que el algoritmo jugó aproximadamente 200,000 juegos de pong, que es bastante, y produjo un total de ~ 800 actualizaciones de los pesos. Si entrenara en la GPU con ConvNets, en unos pocos días, podría lograr excelentes resultados, y si optimizara los hiperparámetros, siempre podría ganar. Sin embargo, no pasé demasiado tiempo computando o configurando,así que en su lugar obtuvimos Pong AI, que ilustra las ideas principales y funciona bastante bien:


.

.También podemos ver los pesos obtenidos de la red neuronal. Gracias al preprocesamiento, cada una de nuestras entradas es una imagen de diferencia de 80x80 (fotograma actual menos fotograma anterior). Cada neurona de la capa W1 está conectada a una capa oculta W2 que consta de 200 neuronas. El número de enlaces es 80 * 80 * 200. Intentemos analizar estas conexiones. Ordenaremos todas las neuronas de la capa W2 y visualizaremos qué pesos llevan a ella. A partir de las escalas que conducen a una neurona W2 de las neuronas W1, haremos imágenes de 80x80. A continuación se muestran 40 imágenes de W2 (un total de 200). Los píxeles blancos son pesos positivos y los negros son negativos. Tenga en cuenta que varias neuronas W2 están sintonizadas en una bola voladora codificada en líneas discontinuas. En un juego, la pelota solo puede estar en un lugar,por lo tanto, estas neuronas son multipropósito y se "dispararán" si la pelota está en algún lugar dentro de estas líneas. La alternancia de blanco y negro es interesante, porque cuando la pelota se mueve a lo largo de la pista, la actividad de la neurona fluctuará como una onda sinusoidal. Y debido a ReLU, solo "disparará" en ciertas posiciones. Hay mucho ruido en las imágenes, lo que sería menor si usara la regularización L2.



Lo que no está pasando Entonces, aprendimos a jugar pong en imágenes usando el gradiente de la función de política, y esto funciona bastante bien. Este enfoque es una forma extraña de "sugerir y verificar", donde "adivinar" se refiere a ejecutar nuestra política en varios episodios del juego, y "verificar" fomenta acciones que conducen a buenos resultados. En general, esto representa el nivel actual de cómo estamos abordando actualmente los problemas del aprendizaje reforzado. Si entiende el algoritmo intuitivamente y sabe cómo funciona, debería estar al menos un poco decepcionado. En particular, ¿cuándo no funciona?

Compare esto con cómo una persona puede aprender a jugar pong. Usted mismo les muestra el juego y dice algo como: "Usted controla la raqueta, y puede moverla hacia arriba y hacia abajo, y su tarea es lanzar la pelota más allá de otro jugador controlado por el programa incorporado", y está listo para comenzar. Tenga en cuenta algunas diferencias:

• - , , , . RL , . , ( ), , . . , , , , , , , , .
  
• , ( , , , ..), ( «» « , , , - - . .). «» / . , , ( ) ( , ).
  
• — (brute force), , . . , , , . , «» , . , , .
  
• , , . , , . .
  

: : RL. , , . , . , 99% . , «» . : «», , - , - , - , , . « , ».

También me gustaría enfatizar el hecho de que, por el contrario, en muchos juegos los gradientes de la política derrotarían fácilmente a una persona. En particular, esto se aplica a los juegos con recompensas frecuentes, que requieren una reacción precisa y rápida y sin planificación a largo plazo. El enfoque PG puede ver fácilmente las correlaciones a corto plazo entre recompensas y acciones. Puedes ver similar en nuestro agente Pong. Desarrolla una estrategia cuando simplemente espera la pelota, y luego se mueve rápidamente para atraparlo solo en el borde, por lo que la pelota rebota a una alta velocidad vertical. El agente gana varias victorias seguidas, repitiendo esta estrategia simple. Hay muchos juegos (Pinball, Breakout) en los que Deep Q-Learning atrae y pisotea a una persona en el barro con sus acciones simples y precisas.

Una vez que comprenda el "truco" con el que funcionan estos algoritmos, podrá comprender sus fortalezas y debilidades. En particular, estos algoritmos están muy por detrás de las personas en la construcción de ideas abstractas sobre juegos que las personas pueden usar para un aprendizaje rápido. Una vez que la computadora mira la matriz de píxeles y nota la llave, la puerta y piensa para sí misma que probablemente sería bueno tomar la llave y llegar a la puerta. Actualmente no hay nada cerca de esto, y tratar de llegar allí es un área activa de investigación.

Cálculos no diferenciables en redes neuronales.Me gustaría mencionar otra aplicación interesante de gradientes de políticas que no son de juego: nos permite diseñar y entrenar redes neuronales utilizando componentes que realizan (o interactúan) con la computación no diferenciable. Esta idea fue introducida por primera vez en 1992 por Williams . y recientemente se ha popularizado en modelos de atención visual recurrente.llamado "atención cercana" en el contexto de un modelo que procesa una imagen con una secuencia de miradas estrechas foveales de baja resolución, similar a cómo nuestro ojo examina objetos con una visión central en funcionamiento. En cada iteración, el RNN recibirá un pequeño fragmento de la imagen y seleccionará la ubicación que debe buscarse más a fondo. Por ejemplo, el RNN puede mirar la posición (5.30), obtener un pequeño fragmento de la imagen, luego decidir mirar (24, 50), etc. Hay una sección de la red neuronal que selecciona dónde buscar más y luego la inspecciona. Desafortunadamente, esta operación no es diferenciable porque no sabemos qué pasaría si tomáramos una muestra en otro lugar. En un caso más general, considere una red neuronal que tiene varias entradas y salidas:



Tenga en cuenta que la mayoría de las flechas azules son diferenciables como de costumbre, pero algunas transformaciones de vista también pueden incluir una operación de selección indiferenciada, que se resalta en rojo. Podemos simplemente pasar por las flechas azules en la dirección opuesta, pero la flecha roja es una dependencia a través de la cual no podemos revertir la propagación del backprop.

¡Política de gradiente al rescate! Pensemos en la parte de la red que realiza el muestreo que puede representarse en función de una política estocástica incrustada en una gran red neuronal. Por lo tanto, durante el entrenamiento, produciremos varios ejemplos (indicados por las ramas a continuación), y luego alentaremos muestras que finalmente conduzcan a buenos resultados (en este caso, por ejemplo, medidos por las pérdidas al final). En otras palabras, entrenaremos los parámetros incluidos en las flechas azules utilizando el backprop, como de costumbre, pero los parámetros incluidos en la flecha roja ahora se actualizarán independientemente del paso hacia atrás utilizando gradientes de políticas, fomentando muestras que resulten en bajas pérdidas. Esta idea también fue recientemente bien enmarcada.Estimación de gradiente utilizando gráficos de cálculo estocásticos.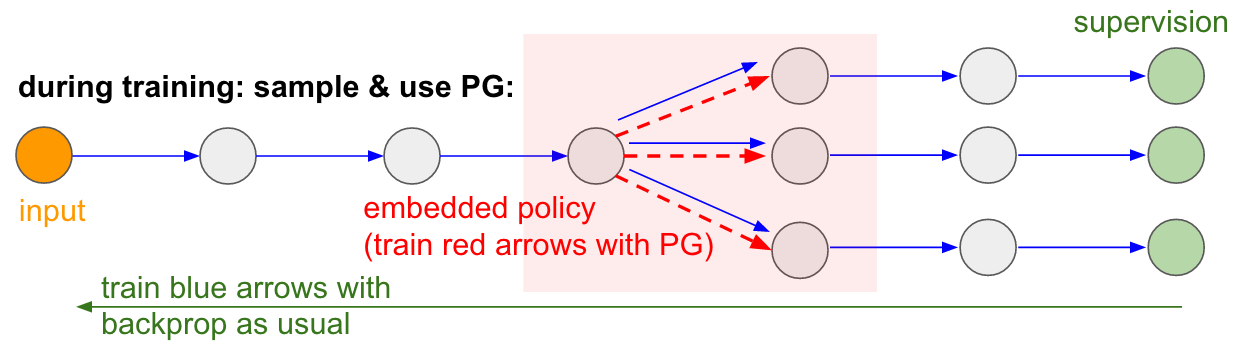



Entrada / salida entrenada en memoria de acceso aleatorio. También encontrarás esta idea en muchos otros artículos. Por ejemplo, la Neural Turing Machine tiene una cinta de memoria con la que leen y escriben. Para realizar una operación de escritura, debe hacer algo como m [i] = x, donde i y x son predichas por la red neuronal RNN. Sin embargo, no hay señal que nos diga qué pasaría con la función de pérdida si escribiéramos j! = I. Por lo tanto, NTM puede realizar operaciones suaves de lectura y escritura. Él predice la función de distribución de atención a, y luego realiza para todo i: m [i] = a [i] * x. Ahora es diferenciable, pero tenemos que pagar un alto precio computacional, clasificando todas las celdas.

Sin embargo, podemos usar gradientes de políticas para teóricamente solucionar este problema, como se hace en RL-NTM. Todavía predecimos la distribución de la atención a, pero en lugar de una búsqueda exhaustiva, seleccionamos al azar lugares para escribir: i = muestra (a); m [i] = x. Durante el entrenamiento, podríamos hacer esto para un pequeño conjunto de i y, al final, encontraríamos un conjunto que funcionaría mejor que otros. Una gran ventaja computacional es que durante las pruebas puede leer / escribir desde una celda. Sin embargo, como se indica en el documento, esta estrategia es muy difícil de poner en práctica, ya que necesita pasar por muchas opciones y casi accidentalmente ir a algoritmos de trabajo. Actualmente, los investigadores coinciden en que PG funciona bien solo cuando hay varias opciones discretas, cuando no es necesario peinar a través de enormes espacios de búsqueda.

Sin embargo, con la ayuda de los gradientes de políticas, y en los casos en que hay disponible una gran cantidad de datos y poder de cómputo, podemos, en principio, soñar con mucho. Por ejemplo, podemos diseñar redes neuronales que aprendan a interactuar con grandes objetos no diferenciables, como los compiladores de Latex. Por ejemplo, para que char-rnn genere código Latex listo para usar, o un sistema SLAM, o solucionadores LQR, o algo más. O, por ejemplo, la superinteligencia puede querer aprender a interactuar con Internet a través de TCP / IP (que tampoco es diferenciable) para acceder a la información necesaria para capturar el mundo. Este es un gran ejemplo.

Conclusiones

Vimos que los gradientes de políticas son un poderoso algoritmo general, y como ejemplo, capacitamos al agente ATARI Pong desde píxeles sin formato desde cero en 130 líneas de Python . En general, el mismo algoritmo puede usarse para entrenar agentes para juegos arbitrarios y, con suerte, algún día podemos usarlo para resolver problemas de control en el mundo real. En conclusión, me gustaría agregar algunos comentarios más:

sobre el desarrollo de la IA. Vimos que el algoritmo funciona mediante la búsqueda de la fuerza bruta, en la que primero vacila al azar y tiene que tropezar con situaciones útiles al menos una vez, e idealmente a menudo, antes de que la función de política cambie sus parámetros. También vimos que una persona aborda estas soluciones a estos problemas de una manera completamente diferente, que se asemeja a la construcción rápida de un modelo abstracto. Dado que estos modelos abstractos son muy difíciles (si no imposibles) de imaginar explícitamente, esta es también la razón por la que recientemente ha habido tanto interés en los modelos generativos y la inducción de software.

Sobre el uso en robótica.El algoritmo no se aplica cuando es difícil obtener una gran cantidad de investigación. Por ejemplo, puede tener uno (o varios) robots interactuando con el mundo en tiempo real. Esto no es suficiente para una aplicación ingenua del algoritmo. Un área de trabajo diseñada para mitigar este problema son los gradientes de política deterministas . En lugar de hacer intentos reales, este enfoque obtiene información de gradiente de una segunda red neuronal (llamada crítica) que modela la función de evaluación. Este enfoque puede, en principio, ser efectivo con acciones de alta dimensión, donde el muestreo aleatorio proporciona una cobertura deficiente. Otro enfoque relacionado es ampliar la robótica que estamos comenzando a ver en Google Robot Farmo tal vez incluso en un Tesla S + con piloto automático.

También hay una línea de trabajo que intenta hacer que el proceso de búsqueda sea menos desesperado al agregar control adicional. Por ejemplo, en muchos casos prácticos, puede obtener la dirección inicial de desarrollo directamente de la persona. Por ejemplo, AlphaGo primero usa la capacitación con un maestro para predecir solo las acciones humanas (por ejemplo , control remoto de robots , aprendizaje , optimización de trayectoria , búsqueda completa de políticas ). Y la política resultante se configura más tarde utilizando PG para lograr el objetivo real: ganar el juego.

En algunos casos, puede haber menos preajustes (por ejemplo, para controlar robots de forma remota ), y existen métodos para usar estos datos previos a la pasantía . Finalmente, si las personas no proporcionan datos o configuraciones específicas, también se pueden obtener en algunos casos mediante el cálculo utilizando métodos de optimización bastante caros, por ejemplo, optimizando la trayectoria en un modelo dinámico conocido (como F = ma en un simulador físico) o en casos cuando se crea un modelo local aproximado (como se ve en una estructura muy prometedora para la búsqueda de políticas administradas).

Sobre el uso de PG en la práctica.Me gustaría hablar más sobre RNN. Creo que podría parecer que los RNN son mágicos y resuelven automáticamente problemas relacionados con secuencias arbitrarias. La verdad es que hacer que estos modelos funcionen puede ser complicado. Se requiere cuidado y experiencia, así como saber cuándo los métodos más simples pueden ayudarlo en un 90%. Lo mismo ocurre con los gradientes de políticas. No funcionan automáticamente así: necesita tener muchos ejemplos, pueden entrenarse para siempre, son difíciles de depurar cuando no funcionan. Siempre debes intentar disparar con una pistola pequeña antes de alcanzar a Bazooka. Por ejemplo, en el caso del entrenamiento de refuerzo, el método de entropía cruzada (CEM) siempre debe verificarse primero., un enfoque estocástico simple de "adivinar y verificar" inspirado en la evolución. Y si insiste en probar gradientes de políticas para su tarea, asegúrese de conocer los trucos específicos. Comience de manera simple y use una opción de PG llamada TRPO , que casi siempre funciona mejor y de manera más consistente que la PG clásica . La idea básica es evitar actualizar la configuración que cambia demasiado su política, debido al uso de la distancia Kulbak-Leibler entre la política antigua y la nueva.

Eso es todo!Espero haberte dado una idea de dónde estamos con Reinforcement Learning, cuáles son los problemas, y si quieres ayudar a promover RL, te invito a hacerlo en nuestro OpenAI Gym :) ¡Nos vemos la próxima vez!

---

Andrej Karpathy,
investigador, desarrollador, director del departamento de IA y piloto automático Tesla

Información adicional:

Deep Learning on Fingers Course 2018
https://habr.com/en/post/414165/ Deep Learning on Fingers

Open Course 2019
https: // habr.com/ru/company/ods/blog/438940/

Facultad de física de NSU
http://www.phys.nsu.ru/