Julia y el método de descenso coordinado

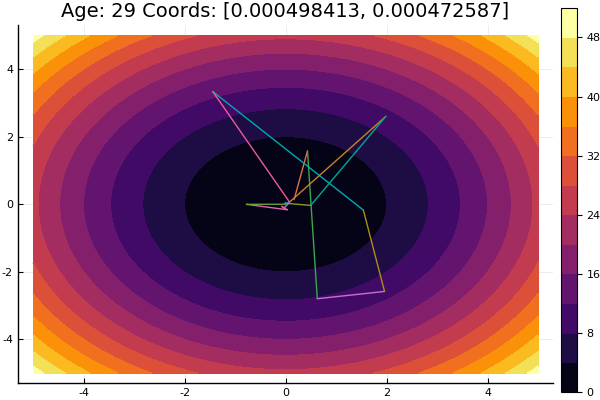
El método de descenso por coordenadas es uno de los métodos más simples de optimización multidimensional y hace un buen trabajo al encontrar un mínimo local de funciones con una topografía relativamente suave, por lo que es mejor comenzar a familiarizarse con los métodos de optimización a partir de él.

La búsqueda del extremo se lleva a cabo en la dirección de los ejes de coordenadas, es decir. durante el proceso de búsqueda, solo se cambia una coordenada. Por lo tanto, un problema multidimensional se reduce a uno unidimensional.

Algoritmo

Primer ciclo:

• $$$x_1 = var$, $$$x_2 = x_2 ^ 0$, $$$x_3 = x_3 ^ 0$, ..., $$$x_n = x_n ^ 0$.
• Buscando funciones extremas $$$f (x_1)$. Ponga el extremo de la función en el punto $$$x_1 ^ 1$.
• $$$x_1 = x_1 ^ 1$, $$$x_2 = var$, $$$x_3 = x_3 ^ 0$, ..., $$$x_n = x_n ^ 0$. Función extrema $$$f (x_2)$es igual a $$$x_2 ^ 1$
• ...
• $$$x_1 = x_1 ^ 1$, $$$x_2 = x_2 ^ 1$, $$$x_3 = x_3 ^ 1$, ..., $$$x_n = var$.
  Como resultado de realizar n pasos, se encontró un nuevo punto de aproximación al extremo $$$(x_1 ^ 1, x_2 ^ 1, ..., x_n ^ 1)$. A continuación, verificamos el criterio para el final de la cuenta: si se cumple, se encuentra la solución, de lo contrario, realizamos un ciclo más.

Preparación

Verifique las versiones del paquete:

(v1.1) pkg> status Status `C:\Users\User\.julia\environments\v1.1\Project.toml` [336ed68f] CSV v0.4.3 [a93c6f00] DataFrames v0.17.1 [7073ff75] IJulia v1.16.0 [47be7bcc] ORCA v0.2.1 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.3 [91a5bcdd] Plots v0.23.0 [ce6b1742] RDatasets v0.6.1 [90137ffa] StaticArrays v0.10.2 [8bb1440f] DelimitedFiles [10745b16] Statistics 

Definimos una función para dibujar las líneas de superficie o nivel en las que sería conveniente ajustar los límites del gráfico:

 using Plots plotly() #   function plotter(plot_fun; low, up) Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for x in Xs, y in Ys ]; plot_fun(Xs, Ys, Zs) xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) #   yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] ) end 

Como función modelo, elegimos un paraboloide elíptico

 parabol(x) = sum(u->u*u, x) fun = parabol plotter(surface, low = [-1 -1], up = [1 1]) 

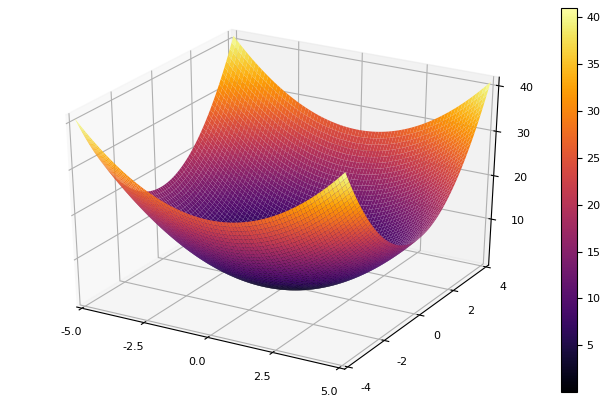
Descenso coordinado

Implementamos el método en una función que toma el nombre del método de optimización unidimensional, la dimensión del problema, el error deseado, la aproximación inicial y las restricciones para dibujar líneas de nivel. Todos los parámetros están configurados a valores predeterminados.

 function ofDescent(odm; ndimes = 2, ε = 1e-4, fit = [.5 .5], low = [-1 -1], up = [1 1]) k = 1 #      sumx = 0 sumz = 1 plotter(contour, low = low, up = up) #    x = [ fit[1] ] #     y = [ fit[2] ] #      while abs(sumz - sumx) > ε && k<80 fitz = copy(fit) for i = 1:ndimes odm(i, fit, ε) #    end push!(x, fit[1]) push!(y, fit[2]) sumx = sum(abs, fit ) sumz = sum(abs, fitz) #println("$k $fit") k += 1 end #     scatter!(x', y', legend = false, marker=(10, 0.5, :orange) );# , ,  p = title!("Age = $(size(x,1)) f(x,y) = $(fun(fit))") end 

A continuación, probaremos varios métodos de optimización unidimensional.

Método de Newton

$$

$$x_ {n + 1} = x_n - \ frac {f (x_n)} {f '(x_n)}$$

La idea del método es simple como es la implementación

 #  dfun = (x, i) -> i == 1 ? 2x[1] + x[2]*x[2] : 2x[2] + x[1]*x[1] function newton2(i, fit, ϵ) k = 1 oldfit = Inf while ( abs(fit[i] - oldfit) > ϵ && k<50 ) oldfit = fit[i] tryfit = fun(fit) / dfun(fit, i) fit[i] -= tryfit println(" $k $fit") k+=1 end end ofDescent(newton2, fit = [9.1 9.1], low = [-4 -4], up = [13 13]) 

Newton es bastante exigente en la aproximación inicial, y sin limitación en los pasos, puede viajar fácilmente a distancias desconocidas. El cálculo de la derivada es deseable, pero se puede prescindir de una pequeña variación. Modificamos nuestra función:

 function newton(i, fit, ϵ) k = 1 oldfit = Inf x = [] y = [] push!(x, fit[1]) push!(y, fit[2]) while ( abs(oldfit - fit[i]) > ϵ && k<50 ) fx = fun(fit) oldfit = fit[i] fit[i] += 0.01 dfx = fun(fit) fit[i] -= 0.01 tryfit = fx*0.01 / (dfx-fx) #        if( abs(tryfit) > abs(fit[i])*10 ) push!(x, fit[1]) push!(y, fit[2]) break end fit[i] -= tryfit #println(" $k $fit") push!(x, fit[1]) push!(y, fit[2]) k+=1 end #  - -   plot!(x, y, w = 3, legend = false, marker = :rect ) end ofDescent(newton, fit = [9.1 9.1], low = [-4 -4], up = [13 13]) 

Interpolación parabólica inversa

Un método que no requiere conocimiento de la derivada y tiene buena convergencia.

 function ipi(i, fit, ϵ) # inverse parabolic interpolation n = 0 xn2 = copy(fit) xn1 = copy(fit) xn = copy(fit) xnp = zeros( length(fit) ) xy = copy(fit) xn2[i] = fit[i] - 0.15 xn[i] = fit[i] + 0.15 fn2 = fun(xn2) fn1 = fun(xn1) while abs(xn[i] - xn1[i]) > ϵ && n<80 fn = fun(xn) a = fn1*fn / ( (fn2-fn1)*(fn2-fn ) ) b = fn2*fn / ( (fn1-fn2)*(fn1-fn ) ) c = fn2*fn1 / ( (fn -fn2)*(fn -fn1) ) xnp[i] = a*xn2[i] + b*xn1[i] + c*xn[i] xn2[i] = xn1[i] xn1[i] = xn[i] xn[i] = xnp[i] fn2 = fn1 fn1 = fn n += 1 println(" $n $xn $xn1") xy = [xy; xn] end fit[i] = xnp[i] plot!(xy[:,1], xy[:,2], w = 3, legend = false, marker = :rect ) end ofDescent(ipi, fit = [0.1 0.1], low = [-.1 -.1], up = [.4 .4]) 

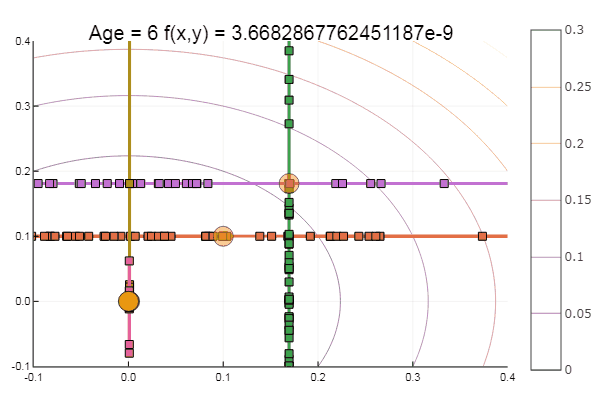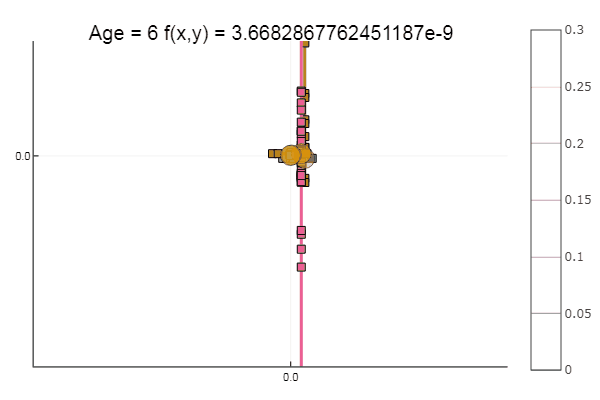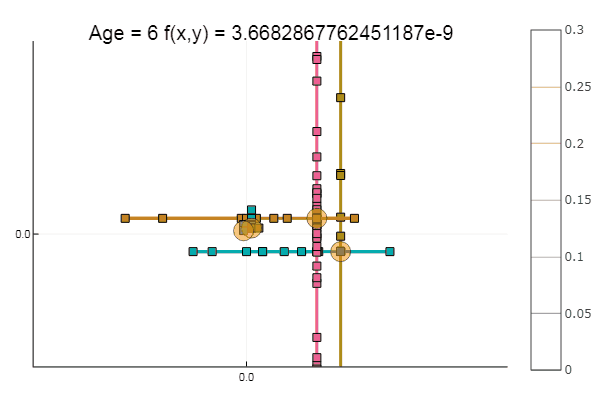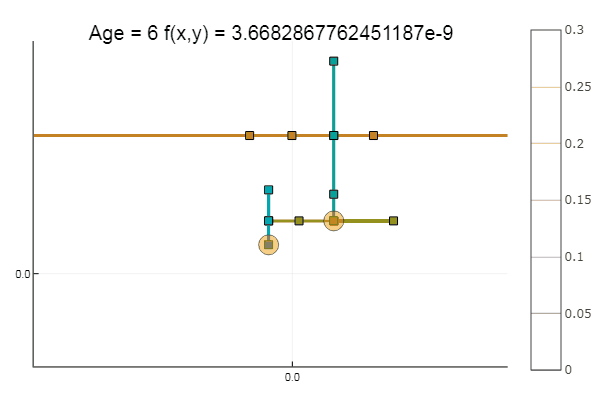
Si empeoramos la aproximación inicial, el método comenzará a requerir un inmenso número de pasos para cada era de descenso coordinado. En este sentido, su hermano gana

Interpolación Parabólica Secuencial

También requiere tres puntos de partida , pero en muchas funciones de prueba muestra resultados más satisfactorios.

 function spi(i, fit, ϵ) # sequential parabolic interpolation n = 0 xn2 = copy(fit) xn1 = copy(fit) xn = copy(fit) xnp = zeros( length(fit) ) xy = copy(fit) xn2[i] = fit[i] - 0.01 xn[i] = fit[i] + 0.01 fn2 = fun(xn2) fn1 = fun(xn1) while abs(xn[i] - xn1[i]) > ϵ && n<200 fn = fun(xn) v0 = xn1[i] - xn2[i] v1 = xn[i] - xn2[i] v2 = xn[i] - xn1[i] s0 = xn1[i]*xn1[i] - xn2[i]*xn2[i] s1 = xn[i] *xn[i] - xn2[i]*xn2[i] s2 = xn[i] *xn[i] - xn1[i]*xn1[i] xnp[i] = 0.5(fn2*s2 - fn1*s1 + fn*s0) / (fn2*v2 - fn1*v1 + fn*v0) xn2[i] = xn1[i] xn1[i] = xn[i] xn[i] = xnp[i] fn2 = fn1 fn1 = fn n += 1 println(" $n $xn $xn1") xy = [xy; xn] end fit[i] = xnp[i] plot!(xy[:,1], xy[:,2], w = 3, legend = false, marker = :rect ) end ofDescent(spi, fit = [16.1 16.1], low = [-.1 -.1], up = [.4 .4]) 

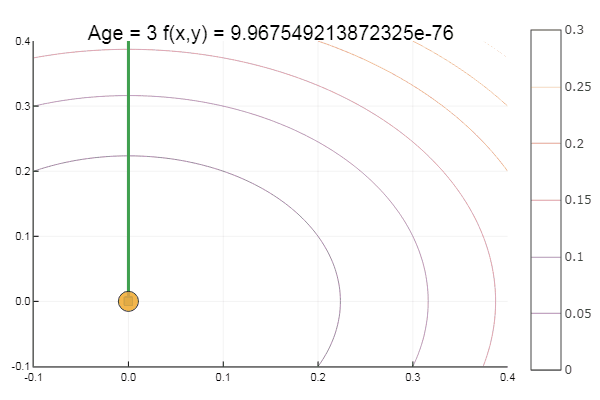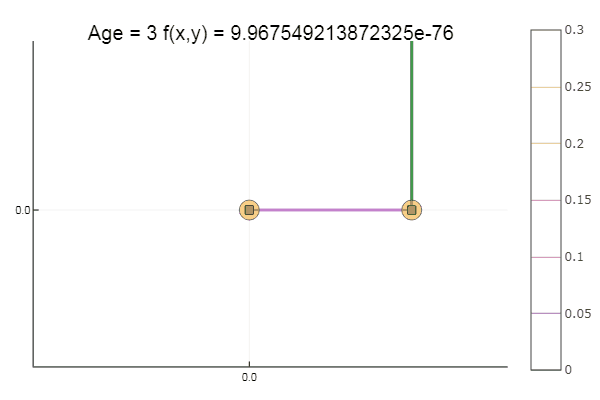
Salir de un punto de partida muy malo vino en tres pasos. Bien ... Pero todos los métodos tienen un inconveniente: convergen a un mínimo local. Ahora tomemos la función de Ackley para investigar

$$

$$f (x, y) = - 20 \ exp \ left [-0.2 {\ sqrt {0.5 \ left (x ^ {2} + y ^ {2} \ right)}} \ right] - \ exp \ left [ 0.5 \ left (\ cos 2 \ pi x + \ cos 2 \ pi y \ right) \ right] + e + 20$$

 ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ # f(0,0) = 0, x_i ∈ [-5,5] fun = ekly plotter(surface, low = [-5 -5], up = [5 5]) 

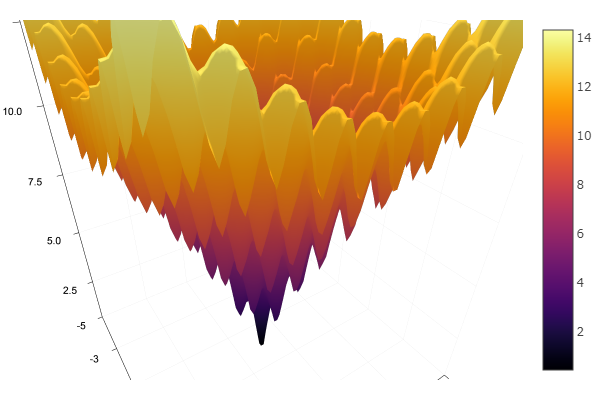
 ofDescent(spi, fit = [1.4 1.4], low = [-.1 -.1], up = [2.4 2.4]) 

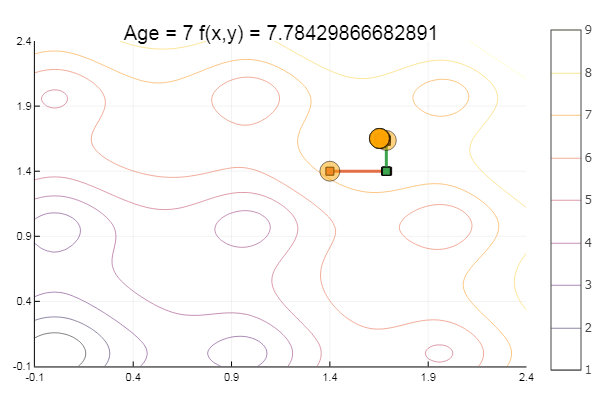
Método de la proporción áurea

Teoría Aunque la implementación es complicada, el método a veces se muestra bien al saltar mínimos locales

 function interval(i, fit, st) d = 0. ab = zeros(2) fitc = copy(fit) ab[1] = fitc[i] Fa = fun(fitc) fitc[i] -= st Fdx = fun(fitc) fitc[i] += st if Fdx < Fa st = -st end fitc[i] += st ab[2] = fitc[i] Fb = fun(fitc) while Fb < Fa d = ab[1] ab[1] = ab[2] Fa = Fb fitc[i] += st ab[2] = fitc[i] Fb = fun(fitc) # println("----", Fb, " ", Fa) end if st < 0 c = ab[2] ab[2] = d d = c end ab[1] = d ab end function goldsection(i, fit, ϵ) ϕ = Base.MathConstants.golden ab = interval(i, fit, 0.01) α = ϕ*ab[1] + (1-ϕ)*ab[2] β = ϕ*ab[2] + (1-ϕ)*ab[1] fit[i] = α Fa = fun(fit) fit[i] = β Fb = fun(fit) while abs(ab[2] - ab[1]) > ϕ if Fa < Fb ab[2] = β β = α Fb = Fa α = ϕ*ab[1] + (1-ϕ)*ab[2] fit[i] = α Fa = fun(fit) else ab[1] = α α = β Fa = Fb β = ϕ*ab[2] + (1-ϕ)*ab[1] fit[i] = β Fb = fun(fit) end println(">>>", i, ab) plot!(ab, w = 1, legend = false, marker = :rect ) end fit[i] = 0.5(ab[1] + ab[2]) end ofDescent(goldsection, fit = [1.4 1.4], low = [-.1 -.1], up = [1. 1.]) 

Eso es todo con descenso coordinado. Los algoritmos de los métodos presentados son bastante simples, por lo que implementarlos en su idioma preferido no es difícil. En el futuro, puede considerar las herramientas integradas del lenguaje Julia , pero por ahora desea sentir todo con sus manos, por así decirlo, considere métodos más complicados y eficientes, luego puede ir a la optimización global, comparándolo simultáneamente con una implementación en otro idioma.

Literatura

1. Zaitsev V.V. Métodos numéricos para físicos. Ecuaciones no lineales y optimización: un tutorial. - Samara, 2005 - 86s.
2. Ivanov A.V. Métodos informáticos para optimizar los sistemas ópticos. Guía de estudio. –SPb: SPbSU ITMO, 2010 - 114s.
3. Popova T. M. Métodos de optimización multidimensional: directrices y tareas para el trabajo de laboratorio en la disciplina "Métodos de optimización" para estudiantes de la dirección "Matemática Aplicada" / comp. T. M. Popova. - Khabarovsk: Editorial del Pacífico. estado Universidad, 2012 .-- 44 p.