Geekly articles weekly

Julia, pendiente descendente y método simplex


Continuamos conociendo los métodos de optimización multidimensional.


A continuación, se propone la implementación del método de descenso más rápido con análisis de la velocidad de ejecución, así como la implementación del método Nelder-Mead por medio del lenguaje Julia y C ++.


Método de descenso de gradiente


La búsqueda del extremo se lleva a cabo en pasos en la dirección del gradiente (max) o anti-gradiente (min). En cada paso en la dirección del gradiente (anti-gradiente), el movimiento se lleva a cabo hasta que la función aumenta (disminuye).


Para la teoría, siga los enlaces:



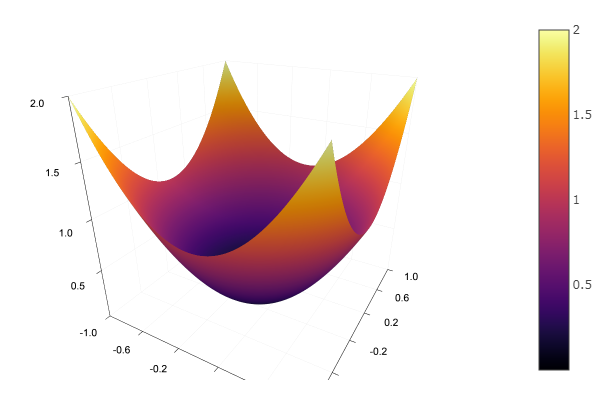
Con la función de modelo, seleccionamos un paraboloide elíptico y establecemos la función de representación en relieve:


using Plots plotly() #   function plotter(plot_fun; low, up) Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for x in Xs, y in Ys ]; plot_fun(Xs, Ys, Zs) xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) #   yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] ) end parabol(x) = sum(u->u*u, x) #   fun = parabol plotter(surface, low = [-1 -1], up = [1 1])


Definimos una función que implementa el método de descenso más pronunciado, que toma la dimensión del problema, la precisión, la longitud del paso, la aproximación inicial y el tamaño del marco del cuadro delimitador:


 # -- ,     -   function ofGradient(; ndimes = 2, ε = 1e-4, st = 0.9, fit = [9.9, 9.9], low = [-1 -1], up = [10 10]) k = 0 while st > ε g = grad(fit, 0.01) fung = fun(fit) fit -= st*g if fun(fit) >= fung st *= 0.5 fit += st*g end k += 1 #println(k, " ", fit) end #println(fun(fit)) end

Puede centrarse en la función que calcula la dirección del gradiente en términos de optimización.


Lo primero que viene a la mente son las acciones con matrices:


 # \delta -      #      function grad(fit, δ) ndimes = length(fit) Δ = zeros(ndimes, ndimes) for i = 1:ndimes Δ[i,i] = δ end fr = [ fun( fit + Δ[:,i] ) for i=1:ndimes] fl = [ fun( fit - Δ[:,i] ) for i=1:ndimes] g = 0.5(fr - fl)/δ modg = sqrt( sum(x -> x*x, g) ) g /= modg end

Lo realmente bueno de Julia es que las áreas problemáticas se pueden probar fácilmente:


 #]add BenchmarkTools using BenchmarkTools @benchmark ofGradient() BenchmarkTools.Trial: memory estimate: 44.14 KiB allocs estimate: 738 -------------- minimum time: 76.973 μs (0.00% GC) median time: 81.315 μs (0.00% GC) mean time: 92.828 μs (9.14% GC) maximum time: 5.072 ms (94.37% GC) -------------- samples: 10000 evals/sample: 1

Puedes apresurarte a volver a escribir todo al estilo Sishny


 function grad(fit::Array{Float64,1}, δ::Float64) ndimes::Int8 = 2 g = zeros(ndimes) modg::Float64 = 0. Fr::Float64 = 0. Fl::Float64 = 0. for i = 1:ndimes fit[i] += δ Fr = fun(fit) fit[i] -= 2δ Fl = fun(fit) fit[i] += δ g[i] = 0.5(Fr - Fl)/δ modg += g[i]*g[i] end modg = sqrt( modg ) g /= modg end @benchmark ofGradient() BenchmarkTools.Trial: memory estimate: 14.06 KiB allocs estimate: 325 -------------- minimum time: 29.210 μs (0.00% GC) median time: 30.395 μs (0.00% GC) mean time: 33.603 μs (6.88% GC) maximum time: 4.287 ms (98.88% GC) -------------- samples: 10000 evals/sample: 1

Pero resulta que, en sí mismo y sin nosotros, sabe qué tipos deben establecerse, por lo que llegamos a un compromiso:


 function grad(fit, δ) #    ndimes = length(fit) g = zeros(ndimes) for i = 1:ndimes fit[i] += δ Fr = fun(fit) fit[i] -= δ fit[i] -= δ Fl = fun(fit) fit[i] += δ g[i] = 0.5(Fr - Fl)/δ end modg = sqrt( sum(x -> x*x, g) ) g /= modg end @benchmark ofGradient() BenchmarkTools.Trial: memory estimate: 15.38 KiB allocs estimate: 409 -------------- minimum time: 28.026 μs (0.00% GC) median time: 30.394 μs (0.00% GC) mean time: 33.724 μs (6.29% GC) maximum time: 3.736 ms (98.72% GC) -------------- samples: 10000 evals/sample: 1

Ahora déjalo dibujar:


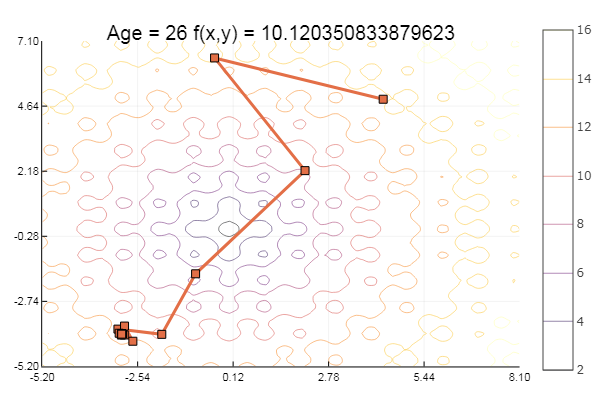
 function ofGradient(; ndimes = 2, ε = 1e-4, st = 0.9, fit = [9.9, 9.9], low = [-1 -1], up = [10 10]) k = 0 x = [] y = [] push!(x, fit[1]) push!(y, fit[2]) plotter(contour, low = low, up = up) while st > ε g = grad(fit, 0.01) fung = fun(fit) fit -= st*g if fun(fit) >= fung st *= 0.5 fit += st*g end k += 1 #println(k, " ", fit) push!(x, fit[1]) push!(y, fit[2]) end plot!(x, y, w = 3, legend = false, marker = :rect ) title!("Age = $kf(x,y) = $(fun(fit))") println(fun(fit)) end ofGradient()


Ahora probemos las funciones de Ackley:


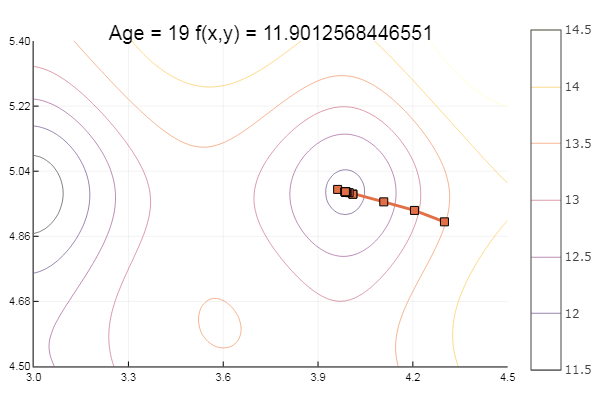
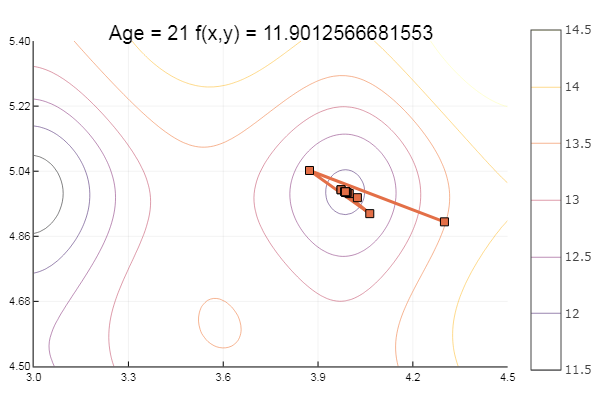
 ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ # f(0,0) = 0, x_i ∈ [-5,5] fun = ekly ofGradient(fit = [4.3, 4.9], st = 0.1, low = [3 4.5], up = [4.5 5.4] )


Cayó en un mínimo local. Vamos a dar más pasos:


 ofGradient(fit = [4.3, 4.9], st = 0.9, low = [3 4.5], up = [4.5 5.4] ) 


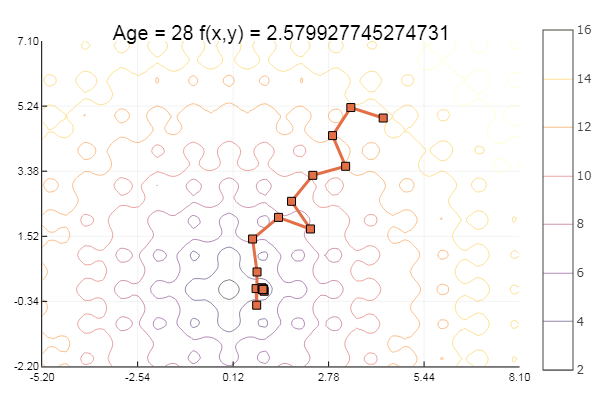
 ofGradient(fit = [4.3, 4.9], st = 1.9, low = [-5.2 -2.2], up = [8.1 7.1] )


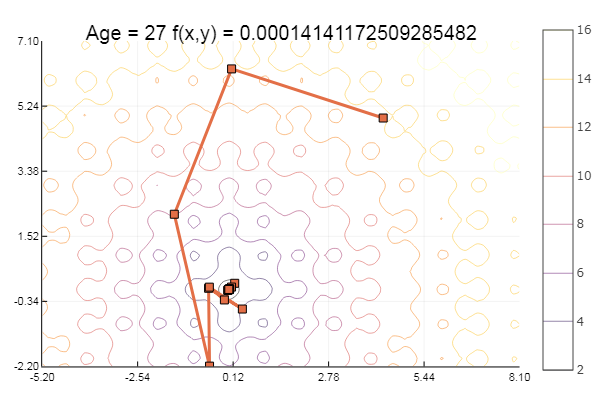
... y un poco más:


 ofGradient(fit = [4.3, 4.9], st = 8.9, low = [-5.2 -2.2], up = [8.1 7.1] )


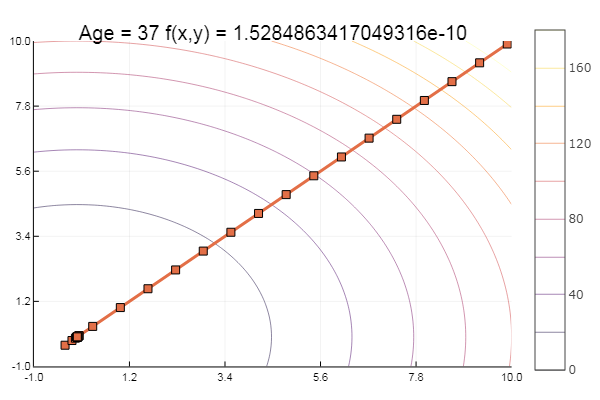
Genial Y ahora algo con un barranco, como la función Rosenbrock:


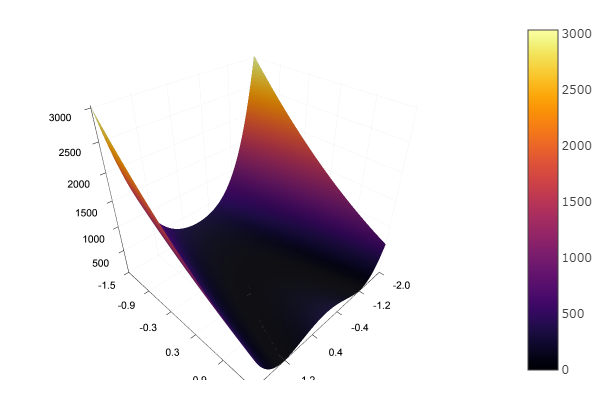
 rosenbrok(x) = 100(x[2]-x[1]*x[1])^2 + (x[1]-1)^2 # f(0,0) = 0, x_i ∈ [-5,5] fun = rosenbrok plotter(surface, low = [-2 -1.5], up = [2 1.5]) 


 ofGradient(fit = [2.3, 2.2], st = 9.9, low = [-5.2 -5.2], up = [8.1 7.1] ) 


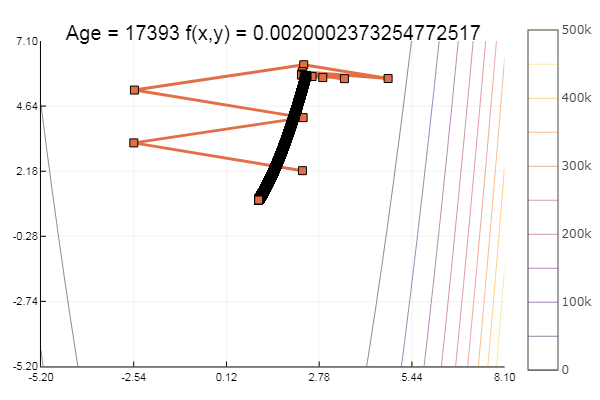
 ofGradient(fit = [2.3, 2.2], st = 0.9, low = [-5.2 -5.2], up = [8.1 7.1] )


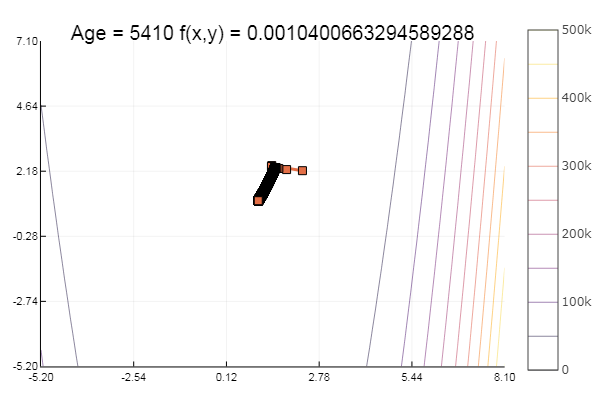
Moralidad: a los gradientes no les gustan los toldos.


Método simplex


El método Nelder-Mead, también conocido como método de poliedro deformable y método simplex, es un método de optimización incondicional de una función de varias variables que no utiliza la derivada (más precisamente, gradientes) de la función y, por lo tanto, es fácilmente aplicable a funciones no suaves y / o ruidosas.


La esencia del método es el movimiento secuencial y la deformación de un simplex alrededor de un punto extremo.


El método encuentra un extremo local y puede estar atrapado en uno de ellos. Si aún necesita encontrar un extremo global, puede intentar elegir un símplex inicial diferente.


Funciones auxiliares:


 #          function sortcoord(Mx) N = size(Mx,2) f = [fun(Mx[:,i]) for i in 1:N] #     Mx[:, sortperm(f)] #Return a permutation vector I that puts v[I] in sorted order. end #   function normx(Mx) m = size(Mx,2) D = zeros(m-1,m) vecl(x) = sqrt( sum(u -> u*u, x) )#   for i = 1:m, j = i+1:m D[i,j] = vecl(Mx[:,i] - Mx[:,j]) #     end D sqrt(maximum(D)) end function simplexplot(xy, low, up) for i = 1:length(xy) if i%11 == 0 low *= 0.05 up *= 0.05 end Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for y in Ys, x in Xs ] contour(Xs, Ys, Zs) xaxis!( low[1]:(up[1]-low[1])*0.2:up[1] ) yaxis!( low[2]:(up[2]-low[2])*0.2:up[2] ) plot!(xy[i][1,:], xy[i][2,:], w = 3, legend = false, marker = :circle ) title!("Age = $if(x,y) = $(fun(xy[i][:,1]))") savefig("$fun $i.png") end end

Y el método simplex en sí mismo:


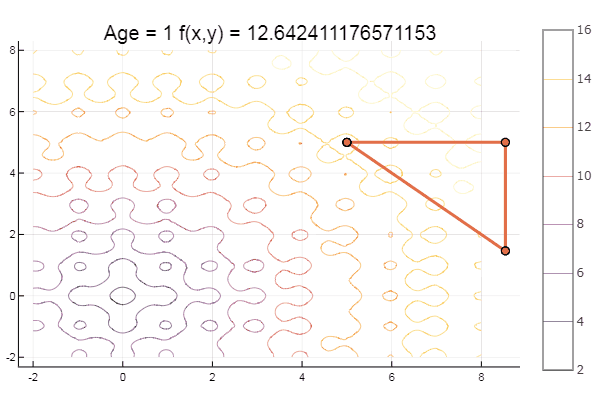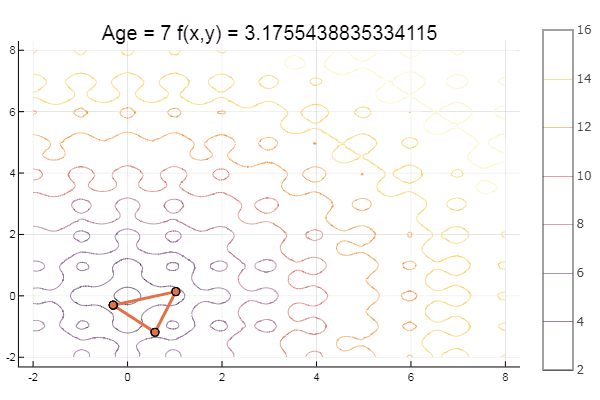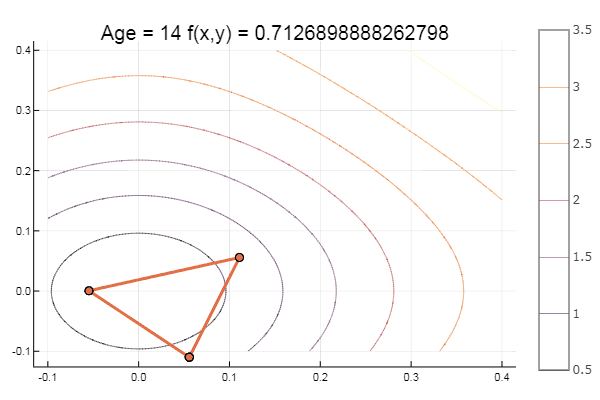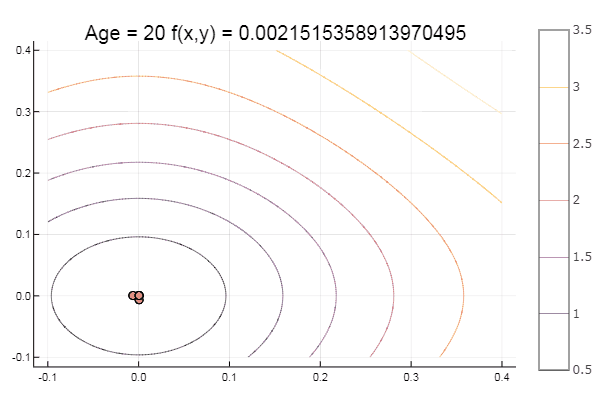
 function ofNelderMid(; ndimes = 2, ε = 1e-4, fit = [.1, .1], low = [-1 -1], up = [1 1]) vecl(v) = sqrt( sum(x -> x*x, v) ) k = 0 N = ndimes Xx = zeros(N, N+1) coords = [] for i = 1:N+1 Xx[:,i] = fit end for i = 1:N Xx[i,i] += 0.5*vecl(fit) + ε end p = normx(Xx) while p > ε k += 1 Xx = sortcoord(Xx) Xo = [ sum(Xx[i,1:N])/N for i = 1:N ] #  - i-  Ro = 2Xo - Xx[:,N+1] FR = fun(Ro) if FR > fun(Xx[:,N+1]) for i = 2:N+1 Xx[:,i] = 0.5(Xx[:,1] + Xx[:,i]) end else if FR < fun(Xx[:,1]) Eo = Xo + 2(Xo - Xx[:,N+1]) if FR > fun(Eo) Xx[:,N+1] = Eo else Xx[:,N+1] = Ro end else if FR <= fun(Xx[:,N]) Xx[:,N+1] = Ro else Co = Xo + 0.5(Xo - Xx[:,N+1]) if FR > fun(Co) Xx[:,N+1] = Co else Xx[:,N+1] = Ro end end end end #println(k, " ", p, " ", Xx[:,1]) push!(coords, [Xx[:,1:3] Xx[:,1] ]) p = normx(Xx) end #while #simplexplot(coords, low, up) fit = Xx[:,1] end ofNelderMid(fit = [-9, -2], low = [-2 2], up = [-8 8])


Y para el postre algo de haya ... por ejemplo, la función de Bukin
f(x,y)=100 sqrt|y−0.01x2|+0.01|x+10|


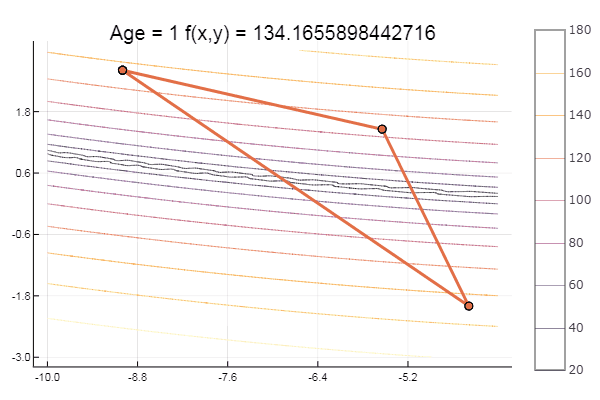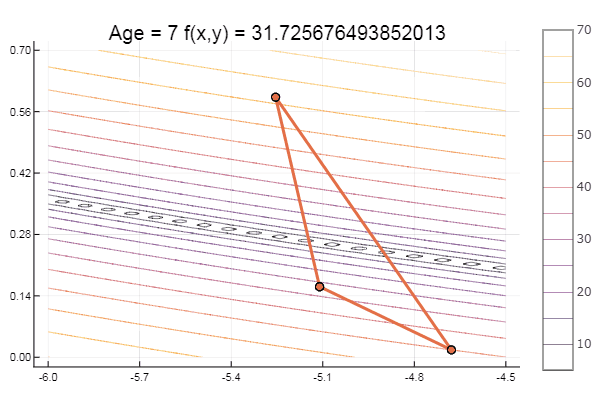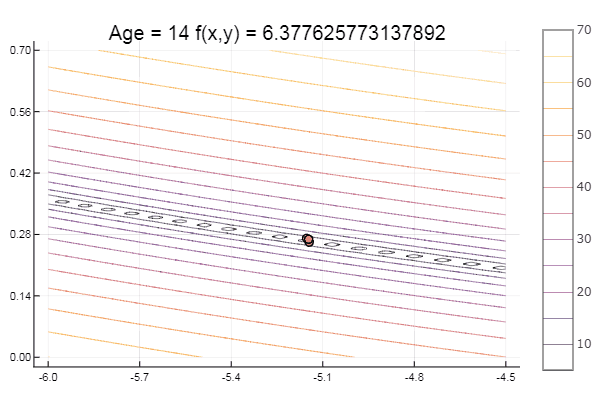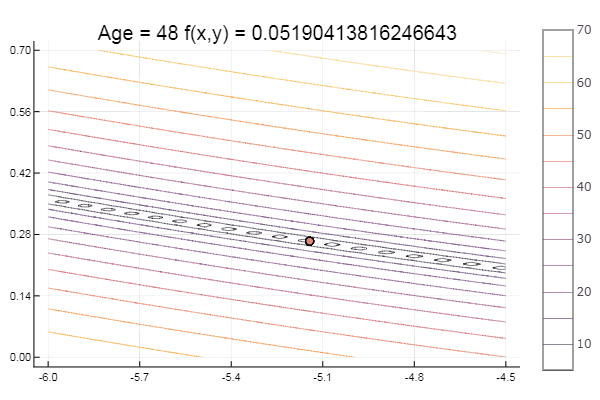
 bukin6(x) = 100sqrt(abs(x[2]-0.01x[1]*x[1])) + 0.01abs(x[1]+10) # f(-10,1) = 0, x_i ∈ [-15,-5; -3,3] fun = bukin6 ofNelderMid(fit = [-10, -2], low = [-3 -7], up = [-8 -4.5])


Mínimo local: bueno, nada, lo principal es elegir el simplex de inicio correcto, así que para mí encontré un favorito.


Bono Métodos de Nelder-Mead, el descenso más rápido y el descenso coordinado en C ++


Alarma! 550 líneas de código!
 /* * File: main.cpp * Author: User * * Created on 3  2017 ., 21:22 */ #include <iostream> #include <math.h> using namespace std; typedef double D; class Model { public: D *fit; D ps; Model(); DI(); }; Model :: Model() { ps = 1; fit = new D[3]; fit[0]=1.3; fit[1]=1.; fit[2]=2.; } D Model :: I() // rosenbrock { return 100*(fit[1]-fit[0]*fit[0]) * (fit[1]-fit[0]*fit[0]) + (1-fit[0])*(1-fit[0]); } class Methods : public Model { public: void ofDescent(); void Newton(int i); void SPI(int i); //sequential parabolic interpolation void Cutters(int i); void Interval(D *ab, D st, int i); void Gold_section(int i); void ofGradient(); void Grad(int N, D *g, D delta); void Srt(D **X, int N); void ofNelder_Mid(); D Nor(D **X, int N); }; void Methods :: ofDescent()//   { int i, j=0; D *z = new D[3]; D sumx, sumz; sumx = sumz = 0; do { sumx = sumz = 0; for(i=0; i<3; i++) z[i] = fit[i]; for(i=0; i<2; i++) { //Cutters(i); //SPI(i); Newton(i); //Gold_section(i); sumx += fit[i]; sumz += z[i]; } j++; //if(j%1000==0) cout << j << " " << fit[0] << " " << fit[1] << " " << fit[2] << " " << fit[3] << endl; //cout << sumz << " " << sumx << endl; } while(fabs(sumz - sumx) > 1e-6); delete[]z; } void Methods :: SPI(int i) { int k = 2; D f0, f1, f2; D v0, v1, v2; D s0, s1, s2; D *X = new D[300]; X[0] = fit[i] + 0.01; X[1] = fit[i]; X[2] = fit[i] - 0.01; while(fabs(X[k] - X[k-1]) > 1e-3) { fit[i] = X[k]; f0 = I(); fit[i] = X[k-1]; f1 = I(); fit[i] = X[k-2]; f2 = I(); v0 = X[k-1] - X[k-2]; v1 = X[k ] - X[k-2]; v2 = X[k ] - X[k-1]; s0 = X[k-1]*X[k-1] - X[k-2]*X[k-2]; s1 = X[k ]*X[k ] - X[k-2]*X[k-2]; s2 = X[k ]*X[k ] - X[k-1]*X[k-1]; X[k+1] = 0.5*(f2*s2 - f1*s1 + f0*s0) / (f2*v2 - f1*v1 + f0*v0); k++; cout << k << " " << X[k] << endl; } fit[i] = X[k]; delete[]X; } void Methods :: Newton(int i) { D dt, T, It; int k=0; while(fabs(T-fit[i]) > 1e-3) { It = I(); T = fit[i]; fit[i] += 0.01; dt = I(); fit[i] -= 0.01; fit[i] -= It*0.001 / (dt - It); cout << k << " " << fit[i] << endl; k++; } } void Methods :: Cutters(int i) { D Tn, Tnm, Tnp, It, Itm; int j=0; Tn = 0.15; Tnm = 2.65;//otrezok Itm = I(); //cout << Tnm << " " << Tn << endl; while(fabs(Tn-Tnm) > 1e-6) { fit[i] = Tn; It = I(); Tnp = Tn - It * (Tn-Tnm) / (It-Itm); cout << j+1 << " " << Tnp << endl; Itm = It; Tnm = Tn; Tn = Tnp; j++; } fit[i] = Tnp; } void Methods :: Interval(D *ab, D st, int i) { D Fa, Fdx, d, c, Fb, fitbox = fit[i]; ab[0] = fit[i]; Fa = I(); fit[i] -= st; Fdx = I(); fit[i] += st; if(Fdx < Fa) st = -st; fit[i] += st; ab[1] = fit[i]; Fb = I(); while(Fb < Fa) { d = ab[0]; ab[0] = ab[1]; Fa = Fb; fit[i] += st; ab[1] = fit[i]; Fb = I(); cout << Fb << " " << Fa << endl; } if(st<0) { c = ab[1]; ab[1] = d; d = c; } ab[0] = d; fit[i] = fitbox; } void Methods :: Gold_section(int i) { D Fa, Fb, al, be; D *ab = new D[2]; D st = 0.5; D e = 0.5*(sqrt(5) - 1); Interval(ab, st, i); al = e*ab[0] + (1-e)*ab[1]; be = e*ab[1] + (1-e)*ab[0]; fit[i] = al; Fa = I(); fit[i] = be; Fb = I(); while(fabs(ab[1]-ab[0]) > e) { if(Fa < Fb) { ab[1] = be; be = al; Fb = Fa; al = e*ab[0] + (1-e)*ab[1]; fit[i] = al; Fa = I(); } if(Fa > Fb) { ab[0] = al; al = be; Fa = Fb; be = e*ab[1] + (1-e)*ab[0]; fit[i] = be; Fb = I(); } cout << ab[0] << " " << ab[1] << endl; } fit[i] = 0.5*(ab[0] + ab[1]); cout << ab[0] << " " << ab[1] << endl; } void Methods :: Grad(int N, D *g, D delta)//   { int n; D Fr, Fl, modG=0; for(n=0; n<N; n++) { fit[n] += delta; Fr = I(); fit[n] -= delta; fit[n] -= delta; Fl = I(); fit[n] += delta; g[n] = (Fr - Fl)*0.5/delta; modG += g[n]*g[n]; } modG = sqrt(modG); for(n=0; n<N; n++) g[n] /= modG; g[N] = I(); } void Methods :: ofGradient() { int n, j=0; D Fun, st, eps; const int N = 2; D *g = new D[N+1]; st = 0.1; eps = 0.000001; while(st > eps) { Grad(N,g,0.0001); for(n=0; n<N; n++) fit[n] -= st*g[n]; Fun = I(); if(Fun >= g[N]) { st /= 2.; for(n=0; n<N; n++) fit[n] += st*g[n]; } j++; cout << j << " " << fit[0]/ps << " " << fit[1]/ps << " " << fit[2]/ps<< endl; } } void Methods :: ofNelder_Mid() { int i, j, k; D modz = 0., p, eps = 1e-3; D FR, FN, F0, FE, FNm1, FC; const int N = 2; D *Co = new D[N]; D *Eo = new D[N]; D *Ro = new D[N]; D *Xo = new D[N]; D **Xx = new D*[N]; D **dz = new D*[N]; for(i=0;i<N;i++) { dz[i] = new D[N]; Xx[i] = new D[N+1]; } for(i=0;i<N;i++) for(j=0;j<N;j++) if(i^j) dz[i][j] = 0; else dz[i][j] = 1; for(i=0;i<N;i++) Xx[i][N] = fit[i]; for(i=0;i<N;i++) modz += fit[i]*fit[i]; modz = sqrt(modz); for(i=0;i<N;i++) dz[i][i] = 0.5*modz; for(i=0;i<N;i++) for(j=0;j<N;j++) Xx[i][j] = fit[i] + dz[i][j]; k = 0; p = Nor(Xx, N); while(p > eps) { k++; Srt(Xx, N); for(i=0;i<N;i++) Xo[i] = 0.; for(i=0;i<N;i++) for(j=0;j<N;j++) Xo[i] += Xx[i][j]; for(i=0;i<N;i++) Xo[i] /= N; for(i=0;i<N;i++) Ro[i] = Xo[i] + (Xo[i]-Xx[i][N]); for(i=0;i<N;i++) fit[i] = Ro[i]; FR = I(); for(i=0;i<N;i++) fit[i] = Xx[i][N]; FN = I(); if(FR > FN) { for(i=0;i<N;i++) for(j=1;j<=N;j++) Xx[i][j] = 0.5*(Xx[i][0] + Xx[i][j]); } else { for(i=0;i<N;i++) fit[i] = Xx[i][0]; F0 = I(); if(FR < F0) { for(i=0;i<N;i++) Eo[i] = Xo[i] +2*(Xo[i] - Xx[i][N]); for(i=0;i<N;i++) fit[i] = Eo[i]; FE = I(); if(FE < FR) for(i=0;i<N;i++) Xx[i][N] = Eo[i]; else for(i=0;i<N;i++) Xx[i][N] = Ro[i]; } else { for(i=0;i<N;i++) fit[i] = Xx[i][N-1]; FNm1 = I(); if(FR <= FNm1) for(i=0;i<N;i++) Xx[i][N] = Ro[i]; else { for(i=0;i<N;i++) Co[i] = Xo[i] +0.5*(Xo[i] - Xx[i][N]); for(i=0;i<N;i++) fit[i] = Co[i]; FC = I(); if(FC < FR) for(i=0;i<N;i++) Xx[i][N] = Co[i]; else for(i=0;i<N;i++) Xx[i][N] = Ro[i]; } } } for(i=0;i<N;i++) cout << Xx[i][0] << " "; cout << k << " " << p << endl; p = Nor(Xx, N); if(p < eps) break; } for(i=0;i<N;i++) fit[i] = Xx[i][0]; /*for(i=0;i<N;i++) { for(j=0;j<N+1;j++) cout << Xx[i][j] << " "; cout << endl; }*/ delete[]Co; delete[]Xo; delete[]Ro; delete[]Eo; for(i=0;i<N;i++) { delete[]dz[i]; delete[]Xx[i]; } } //   D Methods :: Nor(D **X, int N) { int i, j, k; D norm, xij, pn = 0.; for(i=0;i<N;i++) for(j=i+1;j<=N;j++) { xij = 0.; for(k=0;k<N;k++) xij += ( (X[k][i]-X[k][j])*(X[k][i]-X[k][j]) ); pn = sqrt(xij);//    if(norm > pn) norm = pn;//   } return sqrt(norm); } //    void Methods :: Srt(D **X, int N) { int i, j, k; D temp; D *f = new D[N+1]; D *box = new D[N]; D **y = new D*[N+1]; for(i=0;i<N+1;i++)//  y[i] = new D[N+1]; for(i=0;i<N;i++) box[i] = fit[i];//    for(i=0;i<=N;i++) { for(j=0;j<N;j++) fit[j] = X[j][i]; f[i] = I();//     } for(i=0;i<N;i++) fit[i] = box[i];//    for(i=0;i<N;i++) for(j=0;j<=N;j++) y[i][j] = X[i][j]; for(i=0;i<=N;i++) y[N][i] = f[i];//stack(X, f) //    , //     N    for(i=1;i<=N;i++) for(j=0;j<=Ni;j++) if(y[N][j] >= y[N][j+1]) for(k=0;k<=N;k++) { temp = y[k][j]; y[k][j] = y[k][j+1]; y[k][j+1] = temp; } //submatrix   for(i=0;i<N;i++) for(j=0;j<=N;j++) X[i][j] = y[i][j]; /* for(i=0;i<=N;i++) { for(j=0;j<=N;j++) cout << y[i][j] << " "; cout << endl; } */ for(i=0;i<N+1;i++) delete[]y[i]; delete[]box; delete[]f; } int main() { Methods method; //method.ofDescent(); //method.ofGradient(); method.ofNelder_Mid(); return 0; }

Suficiente por hoy. El siguiente paso será lógico para intentar algo de la optimización global, escribir más funciones de prueba y luego estudiar paquetes con métodos integrados.

Source: https://habr.com/ru/post/440070/

More articles:


All Articles