Conocimiento de la red neuronal más simple y su implementación paso a paso.

Una vez me encontré con un libro llamado "Crea tu red neuronal" , escrito por Tarik Rashid . A diferencia de muchos otros libros sobre redes neuronales, en este se presentó todo en un lenguaje simple, con un número suficiente de ejemplos y consejos.

Inspirado en este libro, quiero revisarlo paso a paso, es decir, su parte práctica, escribir el código para una red neuronal simple .
Este artículo es para aquellos que desean participar en redes neuronales y aprendizaje automático, pero hasta ahora tienen dificultades para comprender esta increíble área de la ciencia. El esqueleto más simple del código de una red neuronal se describirá a continuación, de modo que muchos entiendan el principio más simple de construcción e interacción de todo lo que consiste esta red neuronal.




Las teorías sobre el aprendizaje automático y las redes neuronales en el Habré son suficientes. Pero si alguien lo necesita, dejaré algunos enlaces al final del artículo. Y ahora, comenzaremos a escribir código directamente, y escribiremos en Python , recomiendo usar Jupyter-Notebook al escribir código

Paso 1. Inicialización de la red

Primero, por supuesto, necesitamos inicializar todos los componentes activos de nuestra red

# numpy —    Python,        import numpy #  scipy.special , -scipy    , ,  ,      ,       ,   - " " import scipy.special #,      import matplotlib.pyplot #     class neuralNetwork: #     def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate): #     ,   ,   ,  ) #     ,  ,   self.inodes = inputnodes self.hnodes = hiddennodes self.onodes = outputnodes #    , wih -       ,    who-       self.wih = numpy.random.rand(self.hnodes, self.inodes) self.who = numpy.random.rand(self.onodes, self.hnodes) #   -  ,  ,  ,    ,     ,     ,  ,  ,   self.lr = learningrate #  -   self.activation_function = lambda x: scipy.special.expit(x) 

Sigmoide

Esta función pertenece a la clase de funciones continuas, toma un número real arbitrario (es decir, no necesariamente un número entero) en la entrada y proporciona un número real en el rango de 0 a 1 en la salida .

En particular, los números negativos grandes (módulo) se convierten en cero , y los números positivos grandes se convierten en uno .

Su salida se interpreta bien como el nivel de activación de la neurona: desde la ausencia de activación (0) hasta la activación completamente saturada (1).

El sigmoide se expresa mediante la fórmula:



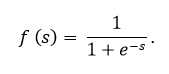
El gráfico de la función sigmoidea de acuerdo con la figura siguiente:



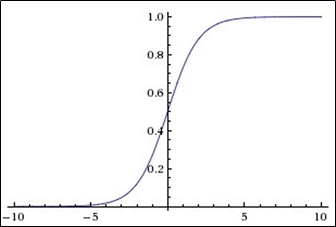
La función sigmoidea es:

• continuo
• aumentando monótonamente;
• diferenciable

En este código, el sigmoide está presente, como puede ver, bajo el nombre expit (x)

Un poco sobre cómo se ve un nodo en una red neuronal

La imagen muestra más ese nodo, solo que generalmente se presenta en forma de círculo, no de rectángulo. Como vemos, dentro de un rectángulo (bien, o un círculo), todo esto es abstracto, hay 2 funciones:

La primera función se dedica al hecho de que recibe toda la información, teniendo en cuenta los pesos, los datos y, a veces, incluso teniendo en cuenta la neurona de desplazamiento (una neurona especial que simplemente permite que los gráficos se muevan y no se mezclen en un montón feo, eso es todo)

La segunda función toma como parámetro el mismo valor que la primera función sumada, y esta segunda función se llama función de activación. En nuestro caso, un sigmoide

Continuamos :

Parte 2. Entrenamiento de redes neuronales

 def train(self, inputs_list, targets_list): #       inputs = numpy.array(inputs_list, ndmin=2).T #     input targets = numpy.array(targets_list, ndmin=2).T #  targets #      hidden_inputs = numpy.dot(self.wih, inputs) #  ,       .    ,       hidden_inputs (1 ),        -   (2 ) hidden_outputs = self.activation_function(hidden_inputs) #    ()  final_inputs = numpy.dot(self.who, hidden_outputs) #  ,     final_outputs = self.activation_function(final_inputs) #   ( - ) output_errors = targets - final_outputs #      ,    <b>  </b>,   <b>       </b>(      ) hidden_errors = numpy.dot(self.who.T, output_errors) #        ( ,      ) self.who += self.lr * numpy.dot((output_errors * final_outputs * (1.0 - final_outputs)), numpy.transpose(hidden_outputs)) #       (       ) self.wih += self.lr * numpy.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)), numpy.transpose(inputs)) 

Y ahora estamos llegando al final

Parte 3. Interrogación de una red neuronal

 #  ,      def query(self, inputs_list): #         inputs = numpy.array(inputs_list, ndmin=2).T #      hidden_inputs = numpy.dot(self.wih, inputs) #  ,     hidden_outputs = self.activation_function(hidden_inputs) #      final_inputs = numpy.dot(self.who, hidden_outputs) #     ,     final_outputs = self.activation_function(final_inputs) return final_outputs 

Lo llevamos al final

 #     ,  ,  (  <b></b>-    , ,   input_nodes = 3 hidden_nodes = 3 output_nodes = 3 #    -   , ... 0.3! learning_rate = 0.3 #   (n    neuralNetwork ,      __init__ ,        n = neuralNetwork(input_nodes,hidden_nodes,output_nodes, learning_rate) 

PS

Arriba se presentó un modelo computacionalmente más simple de una red neuronal. Pero no se mostró ninguna aplicación específica.

Si lo desea, puede ir más allá al agregar la capacidad de reconocer texto escrito a mano en el código MNIST , para esto puede descubrir completamente (y simplemente divertirse) con este archivo jupyter , mi tarea fue demostrar el código y, si es posible, masticar en la red y para que respuestas

PPS

A continuación encontrará enlaces útiles:

1. Enlace a Github Tarik ->
2.Su libro ->
3.Teoría del aprendizaje de máquinas ->
4.Teoría del aprendizaje de máquinas ->
5.Teoría del aprendizaje de máquinas ->