Las pruebas / argumentos de conocimiento cero son una tecnología criptográfica emergente que promete acercarnos al Santo Grial de blockchain: proporcionar privacidad y auditabilidad de los datos.
Las aplicaciones potenciales para conocimiento cero incluyen, pero no se limitan a:
Otra aplicación para pruebas de conocimiento cero es ayudar a las cadenas de bloques a
escalar . Los ZKP permiten la "compresión" de los cálculos para las transacciones de blockchain sin sacrificar la seguridad.
En este artículo, describimos cómo se puede aplicar el conocimiento cero (específicamente, Bulletproofs ) para construir un servicio centrado en la privacidad utilizando la plataforma Exonum de Bitfury.
Análisis situacional
Es posible lograr
cierto nivel de privacidad de datos en las aplicaciones blockchain utilizando el enfoque de "jardín amurallado", donde los datos están ocultos porque el acceso a ellos está restringido con la ayuda de firewalls, control de acceso basado en roles,
fosos y otras medidas de seguridad perimetral . Los datos confidenciales en la cadena de bloques pueden encriptarse (quizás, con un esquema de encriptación de clave pública, con las claves públicas relevantes administradas por la misma cadena de bloques) y / o almacenarse fuera de la cadena de bloques (en este caso, la cadena de bloques solo almacena huellas digitales hash de los datos) Este enfoque se utiliza en muchos marcos contables distribuidos autorizados.
Sin embargo, las desventajas del enfoque de "jardín amurallado" son cada vez más evidentes. Para decirlo sin rodeos, el enfoque es antitético a uno de los principales puntos de venta de blockchain: la auditabilidad. Si los datos en la cadena de bloques no se pueden auditar consultando la lógica del contrato inteligente, la cadena de bloques se convierte en un servicio de
marca de tiempo vinculado glorificado. El hecho de que haya algunos datos en la cadena de bloques ya no significa que estos datos sean válidos según las reglas del contrato inteligente. La segunda desventaja principal del enfoque de jardín amurallado es que no se escala. El CTO de R3, Richard Brown, por ejemplo,
comparó acertadamente el modelo de privacidad de su solución con los canales de Slack: es difícil agregar o eliminar de forma segura a los participantes del jardín, aún más cuando no hay expectativas previas en cuanto al número e identidades de estos participantes
Aquí es donde
el conocimiento cero puede ser valioso. Por diseño, las pruebas y argumentos de conocimiento cero prueban de manera convincente una declaración sobre datos privados sin revelar nada sobre los datos, excepto la declaración que se está probando. ¡Es fácil hacer que las pruebas de conocimiento cero sean
universalmente verificables, sin sacrificar la privacidad! ² Esta característica es exactamente lo que se necesita para construir un sistema que mantenga la privacidad y sea auditable al mismo tiempo.
Nuestra investigacion
Para demostrar el uso de pruebas de conocimiento cero, vamos a construir un servicio de criptomonedas con una funcionalidad similar a los servicios de tutoría en la
documentación de Exonum . El servicio permite registrar usuarios y billeteras (proporcionando un saldo inicial de tokens como recompensa) y transferir tokens entre las partes registradas. Todas las transacciones se autentican con la ayuda de un criptosistema de firma digital, Ed25519, que está integrado en los servicios de Exonum. No ocultamos las identidades de las partes que realizan transacciones (es decir, sus claves públicas), pero ocultamos la cantidad de tokens que se realizan y el saldo de cada cuenta en el sistema. También discutimos cómo podríamos mejorar el servicio para ocultar las entidades de transacción al final del artículo.
El servicio es de código abierto y se puede acceder
aquí .
Fondo de criptografía
Para entender cómo funciona el servicio, primero debemos presentarnos a la primitiva criptográfica central que sustenta Bulletproofs, un concepto llamado
compromisos de Pedersen . Un esquema de compromiso criptográfico es algo así como una función hash: alguien ingresa datos secretos (la apertura) y obtiene la salida que está codificada de manera irreconocible (el compromiso). Entonces se puede revelar la apertura para demostrar que el valor comprometido le corresponde.
La diferencia con las funciones hash es que además de ser
vinculante (nadie puede idear dos aperturas diferentes que produzcan el mismo compromiso), también se espera que se
oculte un esquema de compromiso (es imposible revertir el esquema y producir una apertura dado un compromiso). Una función hash se oculta si su entrada se distribuye uniformemente sobre todo el espacio de entrada, pero esta suposición con frecuencia no se cumple para los compromisos (de hecho, debe ser posible comprometerse con un valor de un conjunto muy pequeño, como Boolean). Como tal, la abertura contiene, además de la carga útil, el
factor de cegamiento que hace (al menos estadísticamente) improbable adivinar la carga útil dado el compromiso.
El esquema de compromiso de Pedersen utiliza un
grupo de primer orden , en el que se cree que el
problema de logaritmo discreto (DLP) es difícil, junto con dos generadores,
G y
H. G y
H deben elegirse de tal manera que se desconozca la relación de registro discreta entre ellos; en otras palabras, nadie sabe
k tal que
H = kG .³ La apertura es un par
(x, r) , donde
x es el valor comprometido y
r es el factor de cegamiento; ambos son escalares grupales (esencialmente, enteros con "desbordamiento" similar a los tipos enteros finitos utilizados en la mayoría de los lenguajes de programación). El compromiso se calcula como
Comm (x; r) = xG + rH . Se puede demostrar que si DLP en el grupo es difícil, el compromiso de Pedersen es computacionalmente vinculante y perfectamente oculto.
La propiedad crucial para los compromisos de Pedersen es que son aditivos: la suma (o diferencia) de 2 compromisos es un compromiso con la suma (o diferencia) de los valores comprometidos. De hecho,
C1 = x1 G + r1 H; C2 = x2 G + r2 H => C1 + C2 = (x1 + x2) G + (r1 + r2) H = Comm(x1 + x2; r1 + r2).
No incluimos los detalles aquí sobre cómo se construyen y verifican las balas, pero se puede encontrar más información en los siguientes recursos: [
1 ] y [
2 ]. Es suficiente tener en cuenta que se supone que el límite superior del límite
M tiene la forma
2 ^ (2 ^ n) , lo que conduce a la construcción de prueba más eficiente.
Construyendo un servicio
Con nuestro conocimiento, podemos ocultar de forma segura los saldos de las cuentas y transferir cantidades con la ayuda de los compromisos de Pedersen. Usando pruebas de rango, podemos probar / verificar que una transferencia es correcta:
- El monto transferido es positivo
- El remitente tiene saldo suficiente en su cuenta.
Para la primera prueba, asumimos el compromiso con el monto de la transferencia,
C_a (está directamente presente en la transacción de transferencia), y verificamos que el valor comprometido en
C_a-Comm (1; 0) se encuentra en el rango
[0, M) . De hecho, esto es equivalente a probar que
C_a corresponde a un valor en el rango
[1, M] . El remitente puede presentar esta prueba, ya que conoce la cantidad transferida
a .
Para la segunda prueba, debemos asumir el compromiso del saldo actual del remitente,
C_s , y verificar que el valor comprometido en
C_s-C_a se encuentre en el rango
[0, M) . Nuevamente, el remitente puede producir esta prueba ya que él / ella conoce la apertura a
C_s y
C_a .
Para aplicar la transferencia al estado blockchain, restamos el compromiso de cantidad
C_a del compromiso de
saldo del remitente (como hemos verificado, no puede conducir a un saldo negativo o al aumento del saldo del remitente), y luego sumamos
C_a al receptor equilibrio compromiso
Detalles clave
Es importante tener en cuenta que hay algunas condiciones que pueden hacer que el servicio implementado sea más complejo.
El receptor de una transferencia debe encontrar la apertura a
C_a desde algún lugar; de lo contrario, deja de conocer la apertura de su equilibrio y ya no puede hacer nada con su billetera. La apertura no está presente en el texto sin formato de la transacción de transferencia (que es el punto completo). Podríamos suponer que el receptor obtiene de manera confiable la apertura a través de un canal fuera de la cadena (por ejemplo, enviado por el remitente a través de Telegram), pero ese no es un escenario ilustrativo. Entonces, en cambio, encriptamos la apertura usando encriptación de clave pública de dos partes basada en el intercambio de claves Diffie-Hellman (libsodium llama a este tipo de
caja de encriptación). Para el beneficio adicional, las claves Curve25519 requeridas para la rutina
box se pueden convertir de las claves Ed25519, por lo que podemos continuar usando un solo par de claves para cada usuario en lugar de introducir claves de cifrado separadas.

Una vez que introducimos el cifrado, ya no podemos aplicar la transferencia atómicamente. De hecho, el remitente puede proporcionar basura de forma maliciosa o involuntaria en lugar del cifrado de apertura, y la lógica de la cadena de bloques no podrá decir que este es el caso. Por lo tanto, solicitamos al receptor que acepte explícitamente la transferencia a través de una transacción separada.
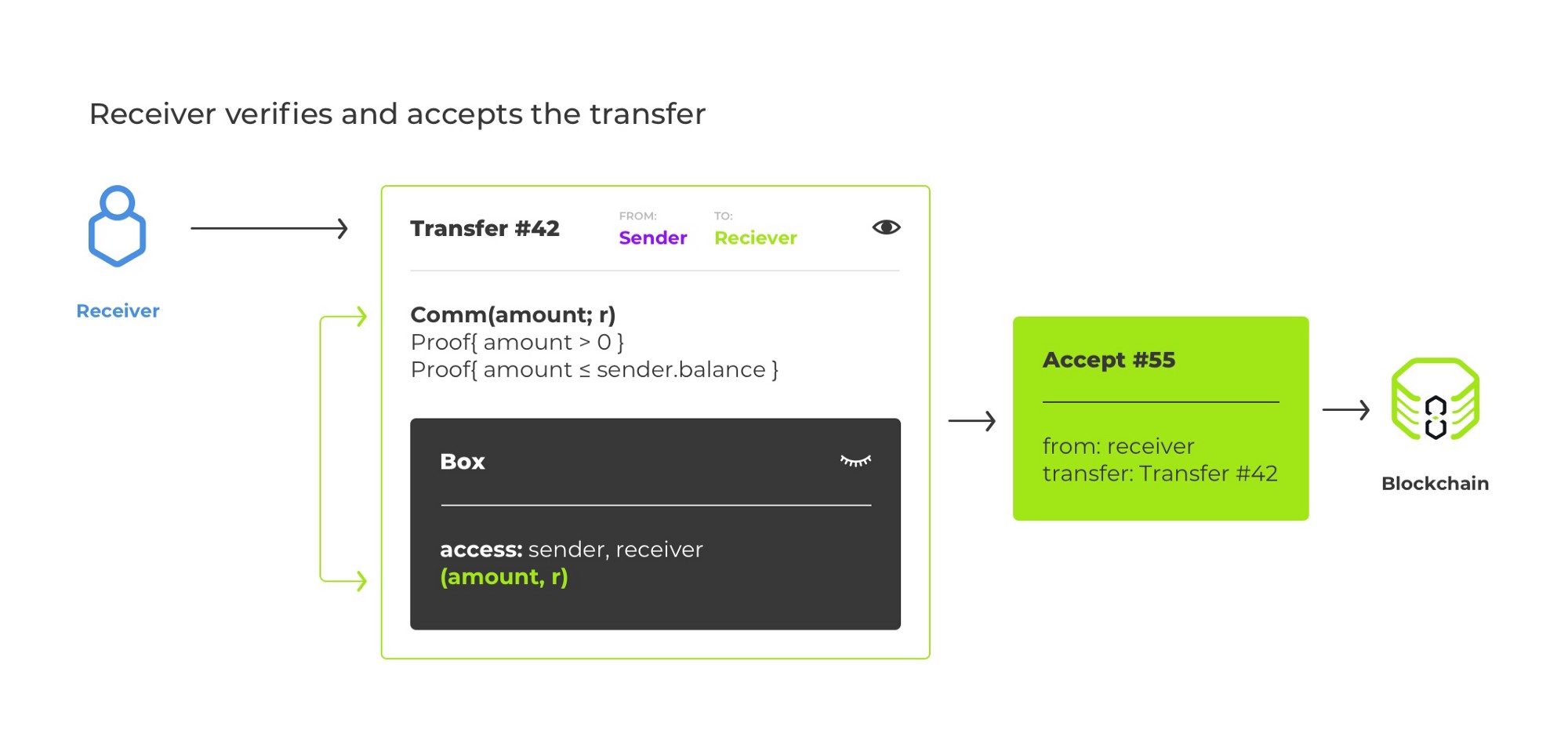
Antes de que se acepte una transferencia, modifica el compromiso de saldo del remitente (de lo contrario, permitiríamos el doble gasto), pero no el del receptor.

Una vez que la red blockchain confirma la transacción de aceptación, se actualiza el saldo del receptor y se completa la transferencia.

Para evitar puntos muertos, una transferencia especifica un retraso de bloqueo de tiempo (en la altura relativa de la cadena de bloques,
como el
CSV de Bitcoin) para que el receptor indique la aceptación. Si el bloqueo de tiempo ha expirado, la transferencia se reembolsará automáticamente al remitente (Exonum lo permite a través de
Service :: beforeCommit () hook).
Otro problema es más complejo. Para producir la prueba de un saldo suficiente, el remitente debe conocer su saldo actual, lo que puede no ser siempre el caso. Una transacción de aceptación perdida o un reembolso pueden aumentar el saldo del remitente sin saberlo; en este caso, la transferencia fallará en la verificación y el remitente se sentirá razonablemente frustrado.
Para aliviar este problema, permitimos que las transferencias hagan referencia a lo que el remitente cree que es su estado actual de billetera (más precisamente, la referencia toma la forma del número de eventos que cambian el saldo de la cuenta: transferencias y reembolsos). Al verificar la prueba de un saldo suficiente, utilizamos el estado de referencia para obtener el compromiso de saldo del remitente. Además, verificamos que no se hayan producido transferencias salientes desde el estado de referencia. Si este es el caso, podemos estar seguros de que si restamos el monto de la transferencia del saldo
actual del remitente, terminaremos con un valor no negativo. De hecho, ¡los eventos en el historial de la cuenta después del punto de referencia (transferencias entrantes y reembolsos) solo pueden aumentar el saldo! ⁷
Con los puntos de referencia en su lugar, el remitente sigue estando algo limitado; No debe tener transferencias pendientes al crear una nueva transferencia. Aún así, esta restricción es mucho menos limitante que el requisito de conocer el estado de la cuenta en el momento de la transferencia; fundamentalmente, hacemos que el remitente dependa de lo
que hizo anteriormente, pero no de las acciones de los demás.
Implementación
Utilizamos una biblioteca a prueba de balas escrita en
Rust puro, que recientemente ha alcanzado
la etapa de prelanzamiento . Dado que la plataforma Exonum está escrita en Rust, se integra perfectamente con la biblioteca. Como beneficio adicional, a diferencia de la versión de prueba de balas descrita en el documento técnico original (que se está desarrollando en
C y utiliza la curva elíptica secp256k1 de Bitcoin), la biblioteca que utilizamos se basa en Curve25519, que ya se usa en Exonum como el componente principal del Ed25519 criptosistema de firma digital.
Implementar el servicio basado en la descripción anterior es bastante sencillo. La parte más difícil fue construir pruebas de Merkle que autentiquen la información devuelta al usuario para que no tenga que confiar ciegamente en los nodos Exonum con los que se comunica. Mejorar la experiencia de los desarrolladores de servicios a este respecto es uno de los principales objetivos de la
versión Exonum 1.0 .
Próximos pasos
El servicio que hemos construido no oculta las identidades del remitente y el receptor de las transferencias, lo cual es una limitación importante para las aplicaciones del mundo real. Afortunadamente, hay formas de resolver este problema.
La técnica genérica utilizada en
zCash (pero aplicable principalmente a otros casos de uso, como
Ethereum ) se basa en la creación de un
árbol Merkle del estado del sistema. Por ejemplo, zCash construye el
árbol de compromiso de notas , que es más o menos equivalente a las salidas de transacciones creadas en Bitcoin. Las pruebas de conocimiento cero luego abarcan rutas de autenticación (también conocidas como ramas de Merkle) en este árbol, revelan algo sobre un elemento del árbol sin revelar a qué elemento se hace referencia. La desventaja de este enfoque es que las funciones hash criptográficas utilizadas para construir árboles Merkle son difíciles de transferir al ámbito de conocimiento cero; las pruebas resultantes se vuelven computacionalmente caras: una sola prueba puede tardar segundos o incluso minutos en crearse. La búsqueda de más funciones hash criptográficas “compatibles con ZKP” es el área de investigación activa.
Si admitimos restricciones adicionales, puede haber una solución más fácil. Por ejemplo, un artículo reciente de
Narula et al . describe un sistema con un número limitado y a priori conocido de participantes, que puede realizar transacciones entre ellos sin revelar participantes o cantidades transferidas para cualquier transacción. (Piense en una red blockchain centrada en la privacidad para las transferencias interbancarias).
En una nota más prosaica, probablemente haya muchas mejoras técnicas que el servicio desarrollado puede disfrutar: más cobertura de prueba, separación de claves de firma y cifrado, evaluación comparativa, etc. Una mejora importante para el servicio UX sería permitir el ordenamiento determinista de transacciones que se originan en el mismo usuario, que planeamos resolver no mucho después de lanzar Exonum 1.0.
Conclusión
Hemos descrito cómo construir un cryptotoken basado en cuentas con una fuerte privacidad habilitada por pruebas de conocimiento cero (específicamente, a prueba de balas). La lógica del token se implementó como un servicio Exonum. Aunque actualmente el servicio es solo una prueba de concepto, muestra cómo la plataforma Exonum se puede utilizar para construir sobre primitivas criptográficas complejas con una sobrecarga muy baja impuesta por el entorno de ejecución.
- Existe una distinción intrincada entre pruebas y argumentos, que no abordaremos aquí. En aras de la simplicidad, nos referiremos a todas las construcciones de conocimiento cero en este artículo como pruebas de conocimiento cero, incluso si esto no siempre es correcto desde el punto de vista teórico.
- Esto se puede lograr a través de una técnica muy general conocida como transformación Fiat - Shamir , que convierte un protocolo de prueba interactivo en uno no interactivo, universalmente verificable. Sacrificando el rigor científico una vez más, no aclararemos explícitamente que las pruebas de conocimiento cero que utilizamos no son interactivas.
- Los generadores generalmente se eligen con el método "nada bajo la manga". Por ejemplo, G puede ser parte de la especificación del grupo para su uso en criptografía de clave pública, y H se deriva de G a través de una función hash: H ~ hash (G) .
- Esto último significa que incluso un adversario con potencia informática infinita no puede deducir a qué se compromete el compromiso; de hecho, si DLP en el grupo se rompe, cada compromiso puede abrirse a cualquier valor posible.
- Esto es parcialmente una decisión de prueba de concepto; en general, reutilizar claves para diferentes propósitos es una mala idea.
- Es teóricamente posible proporcionar una prueba de conocimiento cero para que el valor cifrado sea equivalente al saldo comprometido; sin embargo, aumentaría prohibitivamente la complejidad del sistema.
- Vale la pena mencionar que algunas transferencias que rompen la regla "no hay transferencias salientes desde el estado referenciado" aún pueden ser correctas; simplemente no tenemos forma de verificar esto.