Si no has leído mi primer artículo sobre el tema, te aconsejo que comiences con
él .
Como mencioné una cierta actitud, aunque muy indirecta, hacia los matemáticos financieros, permítanme desarrollar el tema hasta el punto del absurdo en función de cómo se desarrolla en Risk Analytics. Al calcular el precio de una opción, a menudo consideran la sensibilidad de este precio a un conjunto de parámetros. Por ejemplo, cómo cambiará el precio de la opción cuando cambie el precio de la acción para la cual se emite la opción, o cuando cambie la volatilidad del precio de la acción, o la tasa del Banco Central, etc.
Podemos estar interesados en cómo cambia la probabilidad de ganar un juego cuando cambia la probabilidad de ganar un punto. De hecho, queremos calcular la derivada del primero al segundo. El enfoque más simple es evaluarlo a simple vista desde el gráfico. Se puede ver que el máximo se logra en una situación de 50:50. Si las probabilidades de ganar un punto cambian de 0.45 a 0.55, la probabilidad de ganar bádminton aumenta de 0.26 a 0.74, es decir, en 0.48. Una estimación aproximada da una derivada en la región de 5. Es decir, si creces hasta 0,51 (es decir, 51%) con las mismas posibilidades, el aumento en la probabilidad de ganar el juego será de alrededor de 0,05 (o 5%). Del mismo modo, puede calcular la derivada en cualquier otro punto del gráfico.
En las finanzas, generalmente se usa el enfoque de “golpear y correr”, es decir, cambian el parámetro en una pequeña cantidad y calculan el nuevo precio de opción y derivado. Habiendo actuado de manera similar, cito los datos exactos en el gráfico (tomé el cambio en un porcentaje, ligeramente grosero, pero aceptable en esta situación). Para mayor claridad, agregó juegos de hasta 5 y 31 puntos. Por cierto, disparar en biatlón se puede considerar como una fiesta de hasta 5. Esto no es una analogía absoluta, ya que el número total de disparos es fijo. Pero los métodos de solución son casi los mismos.
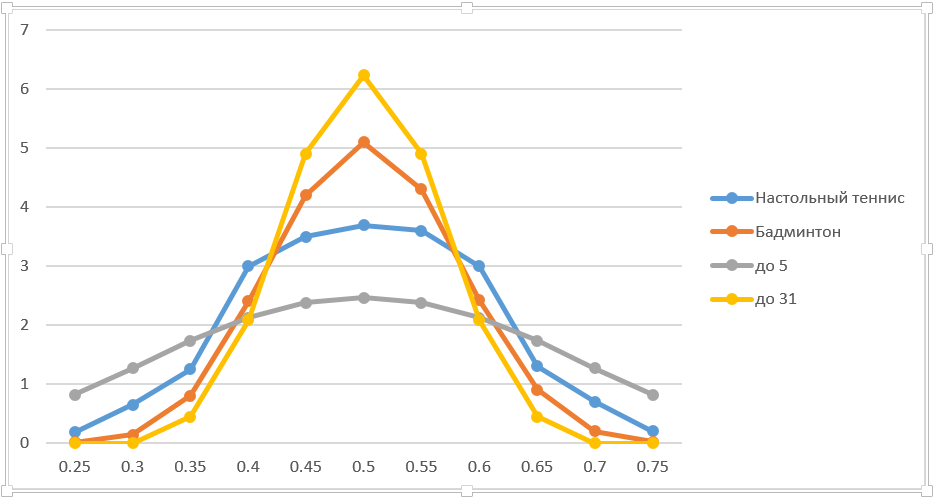
Obviamente, cuanto más largo sea el lote, mayor será la derivada a 50:50. Si la duración del grupo tiende al infinito, la victoria de un jugador con una ventaja mínima está prácticamente garantizada. El ancho de la curva disminuye en consecuencia. En general, las conclusiones son bastante obvias.
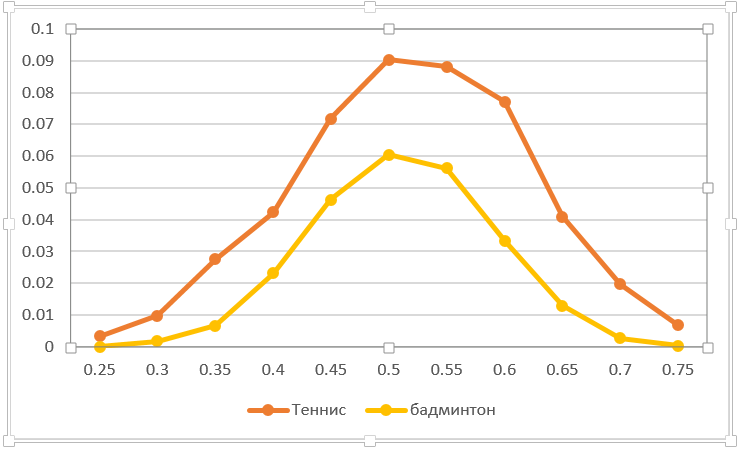
Puede calcular la sensibilidad a la descarga accidental de un punto. Por ejemplo, alimentar en la red. ¿Cuánto afecta un deslizamiento al resultado del juego? De hecho, esta es una reducción en el puntaje ganador para el oponente en un punto. El siguiente gráfico refleja esta situación. Naturalmente, en el tenis de mesa es más crítico perder un punto que en el bádminton. Con fuerzas iguales, la probabilidad del resultado del juego cae tanto como sea posible, de 0.5 a 0.41. Presta atención a la asimetría de las curvas (a diferencia de la mayoría de las otras). Esto no es casualidad. El hecho es que el balance cambia de 50:50 a una mayor probabilidad de ganar un punto, ya que un punto perdido empeora las posibilidades de un jugador.
Pongamos otra experiencia interesante. Imagine que uno de los jugadores puede concentrarse y jugar 3 puntos por encima del promedio (p1 + delta). Suponga que después de esto, la alineación volverá al original (al promedio esperado sin tener en cuenta el "aumento de fuerza"). Está claro que la probabilidad de ganar aumentará. La pregunta es, ¿importa cuándo concentrarse, al principio o al final del juego? Propongo hacer una suposición antes de seguir leyendo.
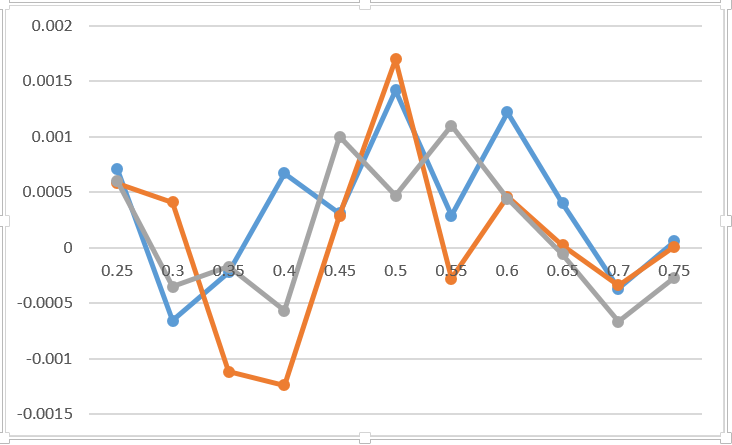
Por lo tanto, como muestra el experimento, no hay absolutamente ninguna diferencia en cuanto a la concentración exacta (los factores del plan moral no se tienen en cuenta). El gráfico muestra la diferencia entre la probabilidad de ganar el juego en caso de concentración en 3 lugares diferentes del juego en comparación con la concentración en los primeros 3 puntos. Creo que este gráfico refleja el error de Monte Carlo y nada más. Agregué 0.2 al resultado del empate de puntos para el primer jugador en tres empates. Ni siquiera indico en el gráfico qué línea corresponde a qué opción. Definitivamente no cambia nada. El único consejo valioso sobre este tema es prepararse antes de que sea demasiado tarde.
Ahora consideremos qué sucederá si uno de los jugadores tiene estabilidad. Los nervios son nervios, sucede un juego responsable. Supongamos que, en promedio, gana el mismo porcentaje de puntos, pero cuando dibuja un punto específico, este porcentaje flota. Por ejemplo, la mitad de los puntos se juegan con probabilidad p1 + delta, y la otra mitad con p1-delta. En este caso, el p1 promedio sigue siendo el original, la pérdida de + delta o –delta ocurre al azar con una probabilidad de 0.5. ¿De alguna manera afectará el resultado del juego? Como demostraron mis experimentos con la ayuda de Monte Carlo, la diferencia prácticamente no se rastrea. De hecho, al sumar o restar una cierta cantidad, aunque al azar, mantenemos la misma probabilidad promedio de ganar un punto. La sugerencia sugiere que la curva de distribución no afecta el resultado del juego, sino solo el promedio, pero no lo asumiré yo mismo. Aquí tienes que pensar.
También me gustaría obtener una ecuación diferencial, como Black Scholes en finanzas, para completar la asociación. Identifique derivados significativos, ponga a cero el componente aleatorio ... También debemos tratar con discreción. Tal vez dejaré esto a matemáticos financieros reales.