¿Cómo ver un color que no existe en la naturaleza?
Hace cuatro años había una publicación en Habré con un video interesante y útil "Cómo funciona el color". Profesor - Dmitry Nikolaev, Jefe del Sector de Sistemas Visuales, IPPI RAS.
Hice una transcripción (a lo mejor de mi comprensión del material), porque considero que tanto el tema es importante como la presentación excelente. Mientras escribía, casi cambié mi φ (λ). Una palabra para el hablante:Hablemos de las matemáticas y la geometría del color, sobre qué estructuras abstractas son inherentes a esta palabra.
¿Qué es el "color"? Nadie lo sabe.
El color es algo de lo que una persona habla, observando y conociendo el mundo a través del ojo.
El ojo registra algunas propiedades de la radiación electromagnética, llamada luz, que ingresa al ojo, se refracta en la lente, proyectada sobre la retina. Los "conos" registran algunas propiedades de potencia. Y luego, de repente, un hombre habla de algún tipo de "color".
En física, no hay color, pero hay propiedades espectrales de la radiación.
"Color" se refiere a la distribución relativa de energía espectral, potencia o flujo de radiación. (Al pasar por un prisma, una persona ve un "arco iris" característico).
Absolutamente, el "color" es un fenómeno psicológico. El color es una sensación que no tiene nada que ver con la física objetiva.
Podemos hablar sobre el color de las cosas - una camisa roja - el "enrojecimiento" de una camisa no está directamente relacionado con la radiación que proviene de esta camisa en el ojo.
El "color" se encuentra en la unión de tres mundos: biología, física, psicología.
El fenómeno de
la constancia del
color (constancia del color) es la capacidad de una persona para operar con el término "color de un objeto", independientemente de lo que haya entrado en el ojo desde un punto específico del objeto.
No conozco un sistema de visión única que tenga una buena consistencia de color (
2014 ). Un automóvil blanco iluminado por una puesta de sol roja: la técnica es incorrecta, el hombre no.
El color es una propiedad de la composición espectral de la radiación. Común a todas las radiaciones. incluyendo y visualmente indistinguible para los humanos.
- Schrödinger
Esta definición es solo la mitad de la verdad. Si el color correspondía solo a la radiación (y no a los objetos además), entonces Schrödinger tenía toda la razón.
El modelo de color más simple en el que trabajó Schrodinger.
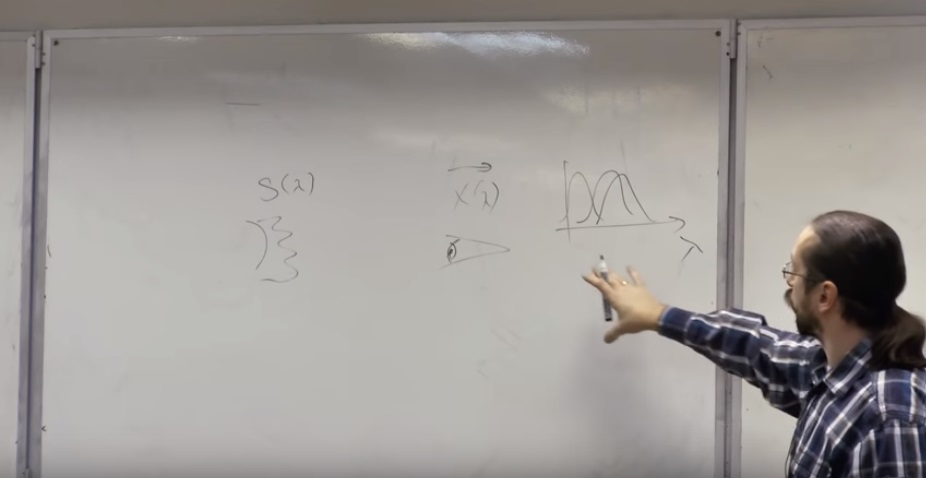
S (λ) es la distribución espectral del flujo de luz. Decimos que este color lleva fotones con diferentes energías. ¿O es la distribución de ondas electromagnéticas con diferentes longitudes de onda?
X (λ) Hay tres tipos de "conos" en el ojo, cada uno caracterizado por un espectro de sensibilidad de cuántos electrones son eliminados de los pigmentos que están en esta célula, dependiendo del fotón que haya absorbido. Este es un vector
Considere una porción físicamente infinitesimal de la retina y diga que en cada punto tenemos tres números:
Cada elemento fotosensible suma todos los fotones a diferentes longitudes de onda. En diferentes tipos de conos. Algunos electrones son eliminados en rojo, algunos en azul, otros en verde.
En realidad, hay algunos algoritmos de interpolación, tanto en la cámara como en la persona.
¿Cómo lograste entender que esta cosa es tridimensional? ¿Qué tiene el vector "a" (eléctricamente difícil de extraer) que tiene tres componentes? Por la tarde Uno de noche, cuatro al anochecer. Pero hablaremos de la visión diurna. Fue posible establecer esto antes de resolverlo con conos, utilizando experimentos colorimétricos.
Schrödinger habló sobre las
condiciones colorimétricas de observación . Solo un área uniformemente luminosa ingresa al campo de visión de una persona, como si una persona mirara al ocular, y solo entra la radiación de una determinada composición espectral. Además, puede nombrar el color que ve. Pero enumerar estos colores no dirá nada sobre la dimensión del espacio de color.
Se realizó el siguiente experimento interesante. El campo de visión humano se dividió en dos áreas. Se aplicó un espectro específico a una región. Se envió una mezcla de varias otras fuentes a la otra mitad. Y a la persona se le permitió girar tantas plumas, la mezcla de cuántas fuentes se alimentaron allí. Y el hombre se vio obligado a responder a la pregunta de si podía colocar los bolígrafos para que no pudiera distinguir visualmente el límite entre la mezcla y la radiación de referencia.
Resultó que si le das a una persona tres asas, siempre puede igualar cualquier radiación. Y todos los demás temas tampoco verán los límites. Dos no pueden. Puede recoger dos bolígrafos y la base inicial, de modo que de ninguna manera puede.
¿Por qué funciona esto en términos de nuestra integral?
Sx
S0
S1
Dado que nuestra integral es una proyección lineal desde un espacio infinito de funciones S.
Si tenemos tres vectores no coplanarios. Siempre hay corrupción, y todas estas cosas no son negativas.
Aquí hay dos ventanas donde puede resumir, pero no restar. Por lo tanto, en lugar de "restar" en una ventana, "sumamos" en otra. Y siempre se puede descomponer en tres radiaciones básicas.
Entonces se demostró que el espacio de color dentro de una persona es
tridimensional .
Esta es una experiencia importante. Y ninguna cantidad de conos encontrados en el ojo humano puede reemplazar esta experiencia. Debido a que el número detectado de diferentes tipos de células fotosensibles en el ojo humano puede limitar la dimensión de este espacio desde arriba. Si hay tres tipos de conos, el espacio de color no es superior a tres.
Las persianas de color tienen solo dos manijas. Tienen un espacio de color diferente. Por lo tanto, es incorrecto decir que "no ven" algo de color. Para ellos, algunos pares de nuestros colores son de un solo color. Y hay infinitos pares de tales. Pero no hay tal parte del espectro que no distingan.
"El verde y el rojo están muy cerca". El experimento lingüístico más simple: cuántos colores puedes nombrar entre verde y azul, y entre verde y rojo.
Esto se debe al hecho de que la concentración de receptores fotosensibles en la región foveal ("verde" y "rojo") es la gran mayoría, y prácticamente no hay azules, se encuentran en la periferia. Por lo tanto, el ojo humano como dispositivo puede, con gran precisión, debido al promedio de muchos conos, evaluar la composición espectral en la región rojo-verde, aunque los detectores mismos muestran señales muy correlacionadas, y la señal azul fuertemente decorelacionada pierde exactamente porque es espacialmente muy rara.
La incomodidad de las inscripciones azules brillantes surge debido al hecho de que las percibimos por el rabillo del ojo y por el rabillo del ojo que no nos gusta mirar.
El principal inconveniente de la definición de Schrodinger es que generalmente ignoraba la forma en que una persona "usa" el color. Una persona no mira la radiación abstracta, mira un color que se refleja desde la superficie.
Por simplicidad, siempre ignoraré por completo la geometría y la indicación de dispersión, y solo hablaré sobre la composición espectral relativa. a medida que cambia el poder, no me molestarán la mayor parte del tiempo. Todas las integrales sobre ángulos sólidos y muchas cosas desagradables desaparecerán.
La "integral" que "vuela" dentro del ojo se ve así:
Aquí es donde crecen todas las sensaciones de color.
Volviendo al experimento con el diente de león, quiero decir que la visión humana resuelve un problema fenomenal, inimaginable. Si consideramos un punto, obviamente es insoluble. Califícalo.
Conocemos estos tres números (vectores "a"), sabemos que como resultado de la autocalibración estas tres funciones X (h). NO sabemos cómo está dispuesto el sol, siempre es diferente, al atardecer, en el cenit, dependiendo de las nubes, las lámparas son multicolores.
La tarea de la visión del color de una persona es evaluar esta función:
Esta función establece el material. Esta función dice fruta madura o no. Queremos determinar esta función por tres números, siempre que se multiplique por otra función desconocida.
Hasta que evaluamos cómo / con qué se iluminó el objeto, no podemos decir nada sobre el color. Si este mecanismo no funcionara, nos confundiríamos si nos mostraran un trozo de papel rojo iluminado en blanco y un trozo de papel blanco iluminado en rojo. Y no estamos confundidos. Hasta a la vista más que solo este pedazo de papel. Si un pedazo de papel cuelga en un vacío, no podemos distinguirlo. Si hay muchos objetos, queda claro de inmediato de qué color es la iluminación, qué papel.
El cerebro resuelve un montón de problemas que no conocemos hasta que tiene que programar el robot, luego comienza a comprender cuánto hace el sistema visual humano.
Colorear
Destaquemos este concepto de la palabra "color". La coloración es una característica objetiva de un objeto físico. Incluso si cierro los ojos, el color no desaparece, es inherente al sujeto mismo, en contraste con el "color", que es una sensación.
Brillo
Hay televisores en blanco y negro y el color casi se puede "eliminar". El componente de potencia del color permanece. Es necesario separar las palabras "brillo" y "ligereza". El brillo se refiere a la radiación, y la luminosidad se refiere a un objeto. El sujeto puede ser brillante y la iluminación brillante. Tanto eso como otro: características de poder, pero pertenecen a mundos diferentes y esto es importante. El coeficiente de reflexión está fijado entre 0 y 1, y la potencia de radiación desde arriba es ilimitada.
Existe un objeto blanco en el mundo blanco y negro, y no hay radiación "blanca" (máxima iluminación brillante).
Saturación
Hay un parámetro naturalmente explicado al hombre. Saturación: qué tan lejos está el color de la escala de grises. La saturación es lo que disminuye cuando se diluye con cualquier color gris. Máxima saturación de radiación láser. (Un poco más adelante hablaremos sobre sustancias químicas psicoactivas).
Tono de color
Esto es lo que queda del color en el espacio de color después de ingresar las dos coordenadas anteriores. A veces confundimos color y matiz. Hay requisitos previos tanto físicos como biológicos para esto.
Color
Esta es la parte de dos componentes del color que no es potente. Si el "brillo" se "desecha" del color de la radiación, entonces el "color" permanece.
Metamerismo
A diferencia de cualquier mujer, un hombre ignora por completo el fenómeno del metamerismo. Todas las chicas saben que no vale la pena comprar una blusa que se ajuste a la falda con luz fluorescente, hasta que la probé con luz natural. Este es un conocimiento intuitivo de la existencia de coloración metamerismo.
El metamerismo de la radiación es cuando sabemos que hay infinitos espectros diferentes que pueden entrar en el ojo para que una persona tenga el mismo sentimiento.
El color (según Schrödinger) es común a todos los espectros que causan la misma sensación.
Manchas de metamerismo . Si dos colores diferentes se ven iguales para alguna S fija, no se deduce que coincidirán con otra S.
Podemos garantizar que coincidirán solo para el mismo φ, es decir, para espectros absolutamente idénticos. Podemos captar espectros de fuentes tan repugnantes, tira, por ejemplo, con algunos picos, que dos colores que parecían ser del mismo color serán diferentes. Y esto es exactamente lo que sucede en las tiendas.
Tres cuartos del problema de la constancia del color es evaluar S (λ) en el punto donde se encuentra el objeto, es decir, evaluar cómo se iluminó. Después de eso, obtenemos una historia similar a las condiciones de observación colorimétrica.
En el oeste, los modelos lineales son ampliamente utilizados. Elegimos tres espectros para que cualquier color se pueda aproximar a una combinación lineal de estos tres colores básicos. Y obtenemos la conexión de los parámetros de color a través de una matriz 3x3. Todo se vuelve hermoso, hay muchos algoritmos, aunque funcionan muy mal. Hay una razón profunda
Y la razón primitiva es que no puede aproximar varios espectros de banda estrecha al mismo tiempo con la suma de tres.
Si hay un pico estrecho que rueda continuamente a lo largo de la escala de longitud de onda, entonces el modelo lineal no puede aproximar todos estos espectros estrechos al mismo tiempo.
¿Hay un modelo que pueda hacer esto? Si lo hay Modelo gaussiano.
Consideramos que φ (λ) es un exponencial de un polinomio de segundo grado. Ella tiene tres parámetros. Ella sabe cómo aproximarse al blanco, se aproxima fácilmente a cualquier espectro estrecho, pero no podrá hacer una serie de "campanas".
Los colores de alta y baja saturación, el modelo gaussiano se aproxima igualmente bien. Esta es una propiedad muy importante. Segunda propiedad:
En nuestra integral, las funciones se multiplican entre sí. Para que los parámetros del modelo no se escapen en ningún lado, es importante que el modelo esté cerrado con respecto a la operación de multiplicación.
Coloración púrpura
Hay un "pero". Hay colores violetas, tienen un espectro de este tipo: fuertemente no cero en la región roja y fuertemente no cero en la región azul, y el gaussiano no puede trabajar con esto. Pero hay un truco.
Si un polinomio con coeficiente cuadrático distinto de cero se encuentra debajo del exponente, entonces nuestro Gaussiano se convierte en una parábola que crece exponencialmente. Y la integral de cero a infinito deja de ser finita, pero como siempre observamos esto a través del ojo, donde los gaussianos tienen tiempo de disminuir más rápido, para esto deben tener un módulo de coeficiente más alto que este color, resulta que la integral se toma como resultado , y podemos trabajar con seguridad con colores violetas no muy saturados y radiación violeta.
Llamarada
¿Cómo evaluar el espectro de una fuente de radiación? Si hacemos esto, entonces al introducir un modelo de color, resolveremos el problema de la constancia del color. Hay varias hipótesis al respecto. Los primeros modelos fueron los siguientes: si una persona ve un objeto blanco en una escena o si ve un resplandor (ve un reflejo de una fuente en una superficie dieléctrica lisa).
Independientemente del color del objeto en sí, el resplandor lleva el espectro de color de la fuente. No hay "multiplicación" al colorear.
Para una primera aproximación, todas las superficies dieléctricas pintadas pueden describirse mediante el modelo dieléctrico de la llamarada de Schaeffer, cuando hay reflejo especular, por ejemplo, del sudor en la frente, y hay reflejo difuso de las partículas de pigmento "en profundidad".
"Componente espejo" - como si fuera un objeto blanco. En el resplandor, cualquier dieléctrico parece blanco. No es así con los metales. El metal liso refleja "su" color. El resplandor del oro es siempre amarillo. El resplandor del cobre es siempre rojo.
El artista ve tres colores en un punto, el resto dos
Otra cosa que complica el concepto de "color" es que cuando miramos un punto, vemos
tres colores a la vez. Lo primero que "vemos" (podemos aprender a ver) es "lo que vino de allí". Para ver esto bien, necesitas un tubo. Si una persona no ve "lo que ha llegado", no puede convertirse en un artista realista. Se requieren muchos trucos y mucho autoaprendizaje para que el artista entienda de qué punto vino y dibuje exactamente "esto". Entonces la imagen será realista. En cambio, el cerebro resuelve tareas útiles (ya que ser artista es completamente inútil en una carrera por la supervivencia). El cerebro determinará qué "cayó" allí. Mirando la calle, entendemos que la hierba está iluminada por el sol poniente. La sombra es azulada porque está iluminada por el cielo. Y al mismo tiempo ves en qué punto el color del objeto. Al mirar un rostro humano, verá el sonrojo más pequeño, porque es evolutivamente extremadamente importante (la niña se sonrojó o no), pero no importa cómo las sombras caigan sobre su rostro, si está iluminado por una puesta de sol o sol del mediodía, o si es un cielo nublado. El problema es que no es el artista quien ve esto al mismo tiempo en dos colores, sin darse cuenta de esto, sino que el artista debe ver tres colores.
Cuando dibujamos lo que vemos en términos de colores, comenzamos a pintar como niños. Y el artista tiene que desactivar muchos algoritmos de visión para convertirse en una "cámara".
Balance de blancos
El "balance de blancos" en las cámaras no significa nada en absoluto. Esto es chamanismo. Como en los libros de cocina: "cocine hasta que esté cocido", "agregue sal y pimienta". Para el fotógrafo, esto tiene sentido, saben lo que cambiará si se gira este asa, pero de hecho no está claro qué es. Supongo que pasa allí, pero es peor que hablar de color. Preferiría no hablar sobre el "balance de blancos", hay que apegarse a la tierra sólida.
Triángulo de color
Tenemos un espacio de color tridimensional en el que viven nuestros vectores.
, llamémoslo RGB para que sea más fácil para los ingenieros informáticos. Y de vuelta a las radiaciones. Alguien brilla en el ojo.
Pregunta: ¿Son posibles combinaciones de R, G y B?
Respuesta: por supuesto que no.
Dibujamos espectros de sensibilidad. Se superponen parcialmente. No son estrictamente cero en ninguna parte, donde otros no son cero. Esto significa que no puede excitar un cono sin excitar, al menos un poco, un cono de un tipo diferente.
Si pudiéramos iluminarnos con un "espectro con energía negativa", podríamos ir a cualquier parte del espacio, incluidos los negativos.
Si brillamos así, todo estará bien, pero es físicamente imposible.
Matemáticamente, uno puede decir esto: todo tipo de espectros de emisión en el espacio original de dimensiones infinitas forma un
cono (no "redondo", sino de álgebra lineal).
Un cono es una estructura tal que si el vector pertenece al cono, entonces el vector multiplicado por el número no negativo también pertenece al cono.
Las funciones no negativas de un argumento con el que bombardeamos nuestros ojos: forman un cono.
Imagine un cubo de dimensiones infinitas y ese "cuadrante", donde todos los ejes son positivos, nuestro cono vivirá allí.
Dado que nuestro ojo realiza una proyección lineal y el espacio RGB, aquí, en el espacio de color, todas las reacciones válidas también formarán un cono. Además, un cono convexo. Esto significa que la suma de dos vectores del cono con coeficientes no negativos también pertenece al cono.Construimos una sección y hacemos una proyección central. El plano de color lo podemos ingresar a su gusto. Desde cero, el brillo crece.En el plano de color, dado que se trata de un cono, debemos tener algún tipo de figura convexa.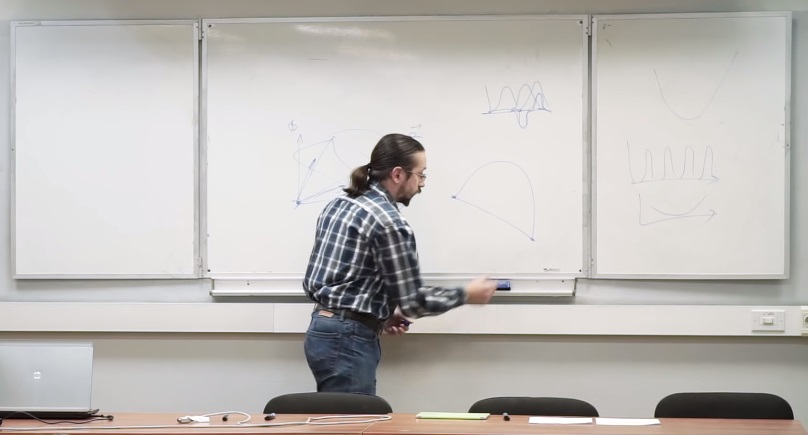
El hecho de que esta cosa se llame triángulo es un humor aparte. Ella tiene dos esquinas. Pero ahora puedo demostrarte fácilmente que, de hecho, el triángulo de color debe tener una esquina. Y esto es obvio. Por qué hay dos de ellos es completamente incomprensible.Recordando cómo se organizan las funciones, y que este es un conjunto convexo, podemos decir que cualquier función se puede recopilar de la suma convexa de las funciones delta.
Los matemáticos me habrían matado por tal cosa, pero ... en el límite. Lo que sea que signifique.Tomemos una discretización tan pequeña-pequeña y digamos que cualquier función dentro de esta discretización es la suma de algunas columnas. Esto significa que cualquier espectro que pueda entrar en nuestros ojos es una combinación convexa de algún tipo de radiación láser, infinitamente estrecha. Esto significa que todo el cono de color es un casco convexo de reacciones a la radiación láser. El triángulo de color es el mismo. CT es el casco convexo de la radiación láser en el plano de color.Comenzamos a mover el láser de ultravioleta a infrarrojo. en el espacio de color vamos alrededor de una especie de bucle.
¿Por qué bucle? Partimos de cero y volvemos a cero.
Debido a que no reaccionamos a los rayos UV, tampoco reaccionamos a los rayos infrarrojos.Algún tipo de trayectoria arbitraria.El hombre está específicamente diseñado para que no haya concavidades:
Este es un bucle. Ella tiene un solo pico. Y proyectamos suavemente esta cosa en el avión. Y ella debería tener un pico. Esto es obvio. En otros lugares, todo es continuo.Pero no
El hecho es que este pliegue se encuentra directamente en el centro de la proyección central. Y los derivados de dos lados diferentes son diferentes.
Este no es un "pico" que converge a una tangente, la tangente a la derecha y la tangente a la izquierda son diferentes.Por lo tanto, la parte UV del "pico" se proyecta aquí:
E IR - aquí:
Y toda la radiación láser vive aquí:
Y para asignar una longitud de onda a cada parte de este arco del triángulo de color.Pero no se pueden atribuir longitudes de onda a esta cosa:
porque aquí se cierra el casco convexo. No hay tales láseres. Esto solo puede ser activado por al menos dos funciones delta.El triángulo de color es un casco convexo sobre las reacciones a la radiación láser.No todos los puntos de nuestro RGB son alcanzables en principio, en física. Hay, como dije, un truco. Puede darle mucho a la persona en la cabeza o tomar cualquier sustancia. ¿Qué es lo mismo para el cerebro? Si ya tenemos en la etapa de procesamiento aparecen números sorprendentes, entonces pueden surgir de tal manera que en la naturaleza no existe. Esto no podría haber venido de un cono. Pero en la corteza visual, bajo la influencia de alguna química o mecánica, tales combinaciones pueden ocurrir. O en un sueño. En un sueño, recibimos señales no de conos. En principio, podemos ver colores que no existen en la naturaleza.Pregunta: ¿Podemos imaginarlo?Respuesta: No puedo decir nada sobre tu imaginación, lo siento. Siendo completamente honesto, ni siquiera puedo decir nada sobre tu existencia, y pides imaginación.Mondrian
Había tal artista: Pete Mondrian . Con Kandinsky y Malevich se le considera el padre de la pintura abstracta.Mondrian tiene pinturas características de rectángulos de varios colores.En la ciencia de las flores, "Mondrian" se ha convertido en un nombre familiar, porque es un objeto imaginario muy bueno, al observar la reacción de una persona que mira a "Mondrian" se puede decir mucho sobre el sistema visual. Al cambiar los colores de la imagen y cambiar la iluminación, puede comprender algo sobre una persona. Por ejemplo, se dieron cuenta de que si hay blanco en la imagen, entonces la persona no confunde la iluminación con el color, si no hay blanco, entonces puede confundirse.Si tomamos el Mondrian, que no deslumbra, es muy mate y lo iluminamos de manera uniforme, y luego cambiaremos todo tipo de colores en el Mondrian. Lo que en el espacio de color (con una X fija (ojo) y S (fuente)) se "recortará".Algunas cámaras fotografían la señal IR del control remoto del televisor en azul. Y esto es solo un mal menor. De hecho, la reproducción del color de cualquier cámara es asquerosa. Pero el poder interpretativo del aparato visual humano es tan grande que lo golpeamos.Una persona ama más los colores saturados, por lo tanto, en los televisores, la saturación se eleva. Para que una persona prefiera mirar televisión y no a través de la ventana. En la ventana, gris y asquerosa, en la televisión, bien.Cuerpo de color
Fijo X, fijo S, cambia φ, pero está sujeto de 0 a 1.Además del punto negro:
hay un punto blanco: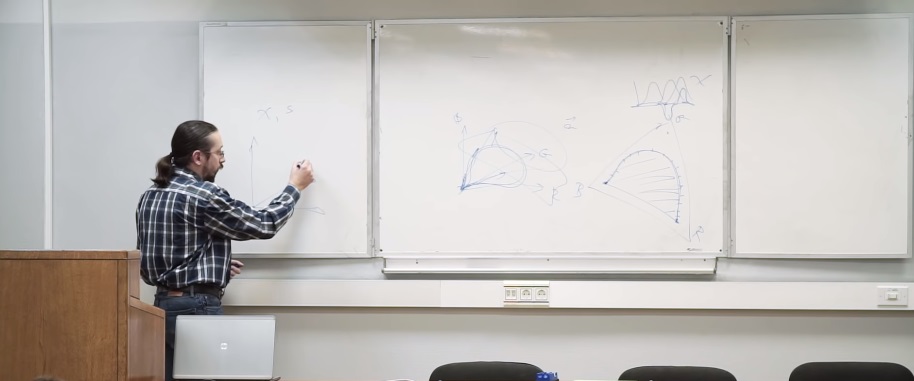
cuando φ es estrictamente igual a 1. Objeto blanco, todo se refleja (si la fuente es amarilla, entonces el "punto amarillo"). No iremos más allá de este punto. Esto ya no es un cono. Que es esto
Esta es una figura simétrica convexa, lenticular.¿Por qué es esto simétrico? Es simple Para cualquier espectro de coloración hay otro, tal que es una unidad menos el primer espectro.Teorema de Maksimov
Si conoce la forma del cuerpo del color, puede reconstruir el espectro S (λ) para todos los λ. Para mí es solo un shock. Desafortunadamente, este no puede ser un buen algoritmo de constancia de color, porque nunca hay tantos colores que una persona observe, y todos se iluminan de manera diferente en términos de potencia.
El sol se ve como una bombilla debajo (amarillo), y el cielo, por el contrario, se parece a una bombilla al rojo vivo (azul). Esta es una pregunta sobre la temperatura del color. Comenzamos a aproximar las fuentes de luz por las fuentes de Planck. Pero la fuente de Planck tiene una temperatura correspondiente. A qué temperatura es necesario calentar un cuerpo completamente negro para que emita dicho espectro.
Puedo tomar todo tipo de:
para cada fuente de Planck, de la que solo hay una familia de un parámetro, puedo construir un cuerpo de color, puedo proyectar este cuerpo de color en el plano de color y no ocupará todo el triángulo de color. Si veo algo en la escena que se cae de esta proyección, puedo excluir esta fuente de la lista de hipótesis sobre cómo se destacó.
En el oeste, esto se llama algoritmo de gama. Cómo aplicar el teorema de Maximov no está claro, porque podemos observar el cuerpo del color solo en el laboratorio.
Tarea de segmentación de color
Hay una tarea más simple que el problema de la constancia del color. La pregunta es, ¿podemos nosotros, mirando la foto, determinar dónde termina un color y dónde comienza otro? Sin nombrar colores. Para decir: aquí hay un salto en la coloración.
Asumimos que no tenemos texturas y acuarelas. Objetos homogéneos, pero diferentes entre sí, dividen el espacio por sí mismos y hay áreas con diferentes colores. Dividir una imagen en estas áreas es la tarea de segmentación de color.
Durante muchos años, las personas pisan el mismo rastrillo. La gente dice: "Veo que toda la mesa es marrón, lo que significa que el programa debería verla". Solo necesita agrupar la distribución del color con un buen algoritmo. No funciona Y nunca funciona. Dado que la premisa original era falsa. Lo que vemos como un objeto del mismo color no puede ser un punto aproximado en un espacio de color de ninguna manera. En la mayoría de los casos Si está iluminado de manera uniforme Mondrian, entonces sí.
Imagine un caballo esférico perfecto en el vacío. Un cierto color. Aquí cuelga y está iluminado por un sol infinitamente distante. Vista lateral Pregunta: ¿cómo se proyectará este caballo en el espacio de color?
La respuesta A diferencia de un caballo plano, un caballo esférico en el espacio de color será un subconjunto de la línea que pasa por el origen.
Con esto, k-means no se las arreglará. Y la mayoría de las cosas se ven así. Y si la esfera también era lisa y no opaca, entonces hay una bengala y tenemos una matriz de dispersión con dos términos, entonces tendremos una suma ponderada de dos colores debajo de la integral, y esta cosa se convertirá en una pieza de un plano que pasa por cero.
Se puede demostrar que en diferentes casos simples de observación de varios objetos y diferentes condiciones de iluminación, se proyectarán objetos de colores uniformes en el espacio de color como submanifolds lineales. No necesariamente a través del paso cero.
Puede ingresar una clasificación de clasificación: a veces estos serán puntos, a veces los planos que pasan a través de la línea acromática. Y de acuerdo con la descripción de la escena, afirmando si la fuente era blanca, si el objeto era liso o si había dos fuentes, una paralela y otra difusa (como el cielo, desde todos los lados), uno puede comprender no solo la dimensión de este submanifold, sino también su posición relativo a cero y la línea acromática.
Resulta que esto es importante, porque podemos decir cómo se proyecta esta cosa en el plano de color, porque si se trata de un subespacio lineal, pierde dimensión cuando se proyecta en un triángulo de color, lo cual es bueno. Y si proyectamos, lo que vemos en el círculo del tono de color, resulta que en muchos casos, incluso si era un avión, en el CT se convirtió en una línea recta que pasa por el punto gris, y por lo tanto se proyectó en un punto en el círculo del color. tonos Y esto es muy importante.
Por lo tanto, una persona selecciona un tono de color como una coordenada separada en el espacio de color, porque es el componente de color más estable durante los cambios de iluminación y observación.
En nuestro espacio de color, hay una línea recta acromática, donde se proyectan espectros iguales a una constante
Equipo fotográfico
Los espectros de sensibilidad de la cámara deben ser una combinación lineal de los humanos, entonces tres elementos sensibles a la luz son suficientes, pero como esto no es así, necesitan más, pero hacen tres y no son reducibles para los humanos, por lo que la reproducción del color del dispositivo está lejos de ser ideal.
Monitores
Curiosamente, la respuesta sobre los monitores es completamente diferente. Un buen monitor debe tener al menos cinco tipos de fuentes de luz. Un monitor solo puede representar una combinación convexa de sus tres colores, y esto siempre es un subconjunto de la verdadera TC humana. Para aproximarlo bien, debe tomar algunos filtros más y aproximarlo con un pentágono. En Estados Unidos, hay una compañía que planea jugar en ella tarde o temprano.
Tintas de impresora
Debido al metamerismo de los colores, debe haber infinitos colores en la impresora. De lo contrario, no será tal que con diferentes fuentes de color la imagen todavía se vea bien. Esta es una de las razones por las cuales las impresoras profesionales tienen una gran cantidad de tintas. Y liberan constantemente "parches" que mejoran el metamerismo cuando se observan con luz fluorescente.
Lena512.tiff
Desde 1973, en la industria del procesamiento de imágenes, se aceptan nuevos algoritmos para probar en la imagen:
Aquí incluso encontraron a esta "Lena".Para los propios evaluadores, la imagen a continuación se extiende
mucho más . Entonces pensé, ¿por qué los expertos en flores no deberían inventar sus propios chistes y la niña en Mandrian puede convertirse en el estándar?