🏪 ↕️ 🤜🏿 Julia y optimización 👩🏻‍🔧 🤽🏾 🚠

Es hora de considerar los paquetes que proporcionan métodos para resolver problemas de optimización. Se pueden reducir muchos problemas para encontrar el mínimo de alguna función, por lo que debe tener un par o dos solucionadores en el arsenal, y aún más un paquete completo.

Entrada

El idioma Julia continúa ganando popularidad . En https://juliacomputing.com puede ver por qué los astrónomos, la robótica y los financieros eligen este idioma, y en https://academy.juliabox.com puede comenzar cursos gratuitos para aprender el idioma y usarlo en cualquier tipo de aprendizaje automático. Para aquellos que decidieron seriamente comenzar a aprender, les aconsejo que vean el video, lean los artículos y hagan clic en las computadoras portátiles de Júpiter en https://julialang.org/learning/ o al menos pasen por el centro de abajo hacia arriba: habrá instalación, características y aplicación para los negocios. urgente Ahora vamos a las bibliotecas.

Blackboxoxptim

BlackBoxOptim : paquete de optimización global para Julia ( http://julialang.org/ ). Admite problemas de optimización de propósitos múltiples y de propósito único y se centra en algoritmos (meta) heurísticos / estocásticos (DE, NES, etc.) que NO requieren que la función optimizada sea diferenciable, a diferencia de los algoritmos deterministas más tradicionales, que a menudo se basan en gradientes / diferenciabilidad. También es compatible con la computación paralela para acelerar la optimización de las funciones que se evalúan lentamente.

Descargue y conecte la biblioteca

]add BlackBoxOptim using BlackBoxOptim

Establezca la función Rosenbrock:

 f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2

Estamos buscando un mínimo en el intervalo (-5; 5) para cada coordenada para un problema bidimensional:

 res = bboptimize(f; SearchRange = (-5.0, 5.0), NumDimensions = 2)

Lo que seguirá la respuesta:

 Starting optimization with optimizer DiffEvoOpt{FitPopulation{Float64},RadiusLimitedSelector,BlackBoxOptim.AdaptiveDiffEvoRandBin{3},RandomBound{RangePerDimSearchSpace}} 0.00 secs, 0 evals, 0 steps Optimization stopped after 10001 steps and 0.12400007247924805 seconds Termination reason: Max number of steps (10000) reached Steps per second = 80653.17866385692 Function evals per second = 81628.98454510146 Improvements/step = 0.2087 Total function evaluations = 10122 Best candidate found: [1.0, 1.0] Fitness: 0.000000000

y muchos datos ilegibles, pero se encontró un mínimo. Como se usa el estocástico, las llamadas a funciones serán un poco excesivas, por lo que para tareas multidimensionales es mejor usar la selección de métodos

 function rosenbrock(x) return( sum( 100*( x[2:end] - x[1:end-1].^2 ).^2 + ( x[1:end-1] - 1 ).^2 ) ) end res = compare_optimizers(rosenbrock; SearchRange = (-5.0, 5.0), NumDimensions = 30, MaxTime = 3.0);

Convexo

Convexo es el paquete de programación convexo disciplinado de Julia (¿programación convexa disciplinaria?). Convex.jl puede resolver programas lineales, programas lineales enteros mixtos y programas convexos compatibles con DCP utilizando varios solucionadores, incluidos Mosek, Gurobi, ECOS, SCS y GLPK, a través de la interfaz MathProgBase. También admite la optimización con variables y coeficientes complejos.

 using Pkg #      Pkg.add("Convex") Pkg.add("SCS")

Hay muchos ejemplos en el sitio: tomografía (el proceso de restaurar la distribución de densidad mediante integrales dadas sobre las áreas de distribución. Por ejemplo, puede trabajar con tomografía en imágenes en blanco y negro), maximizar la entropía, la regresión logística, la programación lineal, etc.

Por ejemplo, debe cumplir las condiciones:

\ begin {array} {ll} \ mbox {satisfar} & \ | x \ | _2 \ leq 100 \\ & e ^ {x_1} \ leq 5 \\ & x_2 \ geq 7 \\ & \ sqrt {x_3 x_4} \ geq x_2 \ end {array}

$\ begin {array} {ll} \ mbox {satisfar} & \ | x \ | _2 \ leq 100 \\ & e ^ {x_1} \ leq 5 \\ & x_2 \ geq 7 \\ & \ sqrt {x_3 x_4} \ geq x_2 \ end {array}$

 using Convex, SCS, LinearAlgebra x = Variable(4) p = satisfy(norm(x) <= 100, exp(x[1]) <= 5, x[2] >= 7, geomean(x[3], x[4]) >= x[2]) solve!(p, SCSSolver(verbose=0)) println(p.status) x.value

Dará una respuesta

 Optimal 4×1 Array{Float64,2}: 0.0 8.554892320716046 15.329934133156783 15.329934133156783

Saltar

JuMP es un lenguaje de optimización matemática específico de dominio integrado en Julia. Actualmente es compatible con varios solucionadores abiertos y comerciales (Artelys Knitro, BARON, Bonmin, Cbc, Clp, Couenne, CPLEX, ECOS, FICO Xpress, GLPK, Gurobi, Ipopt, MOSEK, NLopt, SCS).

JuMP facilita la identificación y resolución de problemas de optimización sin el conocimiento de expertos, pero al mismo tiempo permite a los expertos implementar métodos algorítmicos avanzados, como el uso de arranques "en caliente" efectivos en la programación lineal o el uso de devoluciones de llamada para interactuar con solucionadores de rama y límite. JuMP también es rápido: la evaluación comparativa ha demostrado que puede manejar cálculos a velocidades similares a las herramientas comerciales especializadas como AMPL, al tiempo que mantiene la expresividad de un lenguaje de programación universal de alto nivel. JuMP se puede integrar fácilmente en flujos de trabajo complejos, incluidas simulaciones y servidores web.

Esta herramienta le permite hacer frente a tareas como:

LP = programación lineal
QP = Programación Cuadrática
SOCP = programación cónica de segundo orden (incluidos problemas con restricciones cuadráticas convexas y / o propósito)
MILP = Programación lineal de enteros mixtos
PNL = Programación no lineal
MINLP = programación no lineal entera mixta
SDP = programación semi-definida
MISDP = programación semidefinida entera mixta

El análisis de sus capacidades será suficiente para varios artículos, así que por ahora pasemos a lo siguiente:

Optim

Optim Hay muchos solucionadores disponibles de fuentes gratuitas y comerciales, y muchos ya están envueltos para su uso en Julia. Pocos de ellos están escritos en este idioma. En términos de rendimiento, esto rara vez es un problema, ya que a menudo se escriben en Fortran o C. Sin embargo, los solucionadores escritos directamente en Julia tienen algunas ventajas.

Al escribir el software (paquetes) de Julia para el cual algo necesita ser optimizado, el programador puede escribir su propio procedimiento de optimización o usar uno de los muchos solucionadores disponibles. Por ejemplo, podría ser algo del conjunto NLOpt. Esto significa agregar una dependencia que no está escrita en Julia, y debe hacer más suposiciones sobre el entorno en el que se encuentra el usuario. ¿Tiene el usuario compiladores adecuados? ¿Puedo usar el código GPL en un proyecto?

También es cierto que usar un solucionador escrito en C o Fortran hace que sea imposible usar una de las principales ventajas de Julia: el envío múltiple. Dado que Optim está completamente escrito en Julia, actualmente podemos usar un sistema de despacho para facilitar el uso de preajustes personalizados. Una característica planificada en esta dirección es permitir una selección de solucionadores dirigida por el usuario para las diversas etapas del algoritmo, basada completamente en el despacho en lugar de en las capacidades predefinidas elegidas por los desarrolladores de Optim.

Un paquete en Julia también significa que Optim tiene acceso a funciones de diferenciación automática a través de paquetes en JuliaDiff .

Guia

Proceder:

 ]add Optim using Optim #   f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2 x0 = [0.0, 0.0] optimize(f, x0)

Recibimos una respuesta con un informe conveniente:

 Results of Optimization Algorithm * Algorithm: Nelder-Mead #   * Starting Point: [0.0,0.0] * Minimizer: [0.9999634355313174,0.9999315506115275] * Minimum: 3.525527e-09 * Iterations: 60 * Convergence: true * √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true * Reached Maximum Number of Iterations: false * Objective Calls: 118

¡Y compáralo con mi Nelder Mead!

spoiler

El mío será más lento :(

Escondido

 using BenchmarkTools @benchmark optimize(f, x0) BenchmarkTools.Trial: memory estimate: 11.00 KiB allocs estimate: 419 -------------- minimum time: 39.078 μs (0.00% GC) median time: 43.420 μs (0.00% GC) mean time: 53.024 μs (15.02% GC) maximum time: 59.992 ms (99.83% GC) -------------- samples: 10000 evals/sample: 1

En el curso de la verificación, también resultó que mi implementación no funciona si usa la aproximación inicial (0, 0). Como criterio de detención, puede usar el volumen del símplex , pero yo uso la norma de una matriz compuesta de vértices. Aquí puedes leer sobre la interpretación geométrica de la norma. En ambos casos, se obtiene una matriz de ceros, un caso especial de una matriz degenerada; por lo tanto, el método no realiza ningún paso. Puede configurar la creación de un símplex inicial, por ejemplo, estableciendo la distancia de sus vértices desde la aproximación inicial (y no como la mía: la mitad de la longitud del vector, fu, qué pena ...), entonces la configuración del método será más flexible, o asegúrese de que todos los vértices no sean se sentó en un punto:

  for i = 1:N+1 Xx[:,i] = fit end for i = 1:N Xx[i,i] += 0.5*vecl(fit) + ε end

Bueno, sí, mi simplex goraaazdo es más lento:

 ofNelderMid(fit = [0, 0.]) step= 118 7.7234e-5 f = 2.797-18 x = [1.0, 1.0] @benchmark ofNelderMid(fit = [0., 0.]) BenchmarkTools.Trial: memory estimate: 394.03 KiB allocs estimate: 6632 -------------- minimum time: 717.221 μs (0.00% GC) median time: 769.325 μs (0.00% GC) mean time: 854.644 μs (5.04% GC) maximum time: 50.429 ms (98.01% GC) -------------- samples: 5826 evals/sample: 1

Ahora más razones para volver al paquete de estudio.

Puedes elegir el método utilizado:

 optimize(f, x0, LBFGS()) Results of Optimization Algorithm * Algorithm: L-BFGS * Starting Point: [0.0,0.0] * Minimizer: [0.9999999926662504,0.9999999853325008] * Minimum: 5.378388e-17 * Iterations: 24 * Convergence: true * |x - x'| ≤ 0.0e+00: false |x - x'| = 4.54e-11 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: false |f(x) - f(x')| = 5.30e-03 |f(x)| * |g(x)| ≤ 1.0e-08: true |g(x)| = 9.88e-14 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 67 * Gradient Calls: 67

y obtener documentación detallada y referencias a ella

 ?LBFGS()

Puede configurar funciones jacobianas y hessianas

 function g!(G, x) G[1] = -2.0 * (1.0 - x[1]) - 400.0 * (x[2] - x[1]^2) * x[1] G[2] = 200.0 * (x[2] - x[1]^2) end function h!(H, x) H[1, 1] = 2.0 - 400.0 * x[2] + 1200.0 * x[1]^2 H[1, 2] = -400.0 * x[1] H[2, 1] = -400.0 * x[1] H[2, 2] = 200.0 end optimize(f, g!, h!, x0) Results of Optimization Algorithm * Algorithm: Newtons Method * Starting Point: [0.0,0.0] * Minimizer: [0.9999999999999994,0.9999999999999989] * Minimum: 3.081488e-31 * Iterations: 14 * Convergence: true * |x - x'| ≤ 0.0e+00: false |x - x'| = 3.06e-09 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: false |f(x) - f(x')| = 3.03e+13 |f(x)| * |g(x)| ≤ 1.0e-08: true |g(x)| = 1.11e-15 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 44 * Gradient Calls: 44 * Hessian Calls: 14

Como puede ver, él desarrolló automáticamente el método de Newton. Y así puede configurar el área de búsqueda y usar el descenso de gradiente:

 lower = [1.25, -2.1] upper = [Inf, Inf] initial_x = [2.0, 2.0] inner_optimizer = GradientDescent() results = optimize(f, g!, lower, upper, initial_x, Fminbox(inner_optimizer)) Results of Optimization Algorithm * Algorithm: Fminbox with Gradient Descent * Starting Point: [2.0,2.0] * Minimizer: [1.2500000000000002,1.5625000000000004] * Minimum: 6.250000e-02 * Iterations: 8 * Convergence: true * |x - x'| ≤ 0.0e+00: true |x - x'| = 0.00e+00 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: true |f(x) - f(x')| = 0.00e+00 |f(x)| * |g(x)| ≤ 1.0e-08: false |g(x)| = 5.00e-01 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 84382 * Gradient Calls: 84382

Bueno, o no sé, digamos que quisiste resolver la ecuación

 f_univariate(x) = 2x^2+3x+1 optimize(f_univariate, -2.0, 1.0) Results of Optimization Algorithm * Algorithm: Brents Method * Search Interval: [-2.000000, 1.000000] * Minimizer: -7.500000e-01 * Minimum: -1.250000e-01 * Iterations: 7 * Convergence: max(|x - x_upper|, |x - x_lower|) <= 2*(1.5e-08*|x|+2.2e-16): true * Objective Function Calls: 8

y él te eligió el Método Brent .
O teniendo datos experimentales, necesita optimizar los coeficientes del modelo

F (p_{1}, p_{2}, x) = p_{1} c o s (p_{2} x) + p_{2} s i n (p_{1} x)

$F (p_1, p_2, x) = p_1 \ cos (p_2x) + p_2 \ sin (p_1x)$

p_{1} = 1, p_{2} = 0.2

$p_1 = 1, p_2 = 0.2$

 F(p, x) = p[1]*cos(p[2]*x) + p[2]*sin(p[1]*x) model(p) = sum( [ (F(p, xdata[i]) - ydata[i])^2 for i = 1:length(xdata)] ) xdata = [-2,-1.64,-1.33,-0.7,0,0.45,1.2,1.64,2.32,2.9] ydata = [0.699369,0.700462,0.695354,1.03905,1.97389,2.41143,1.91091,0.919576,-0.730975,-1.42001] res2 = optimize(model, [1.0, 0.2]) Results of Optimization Algorithm * Algorithm: Nelder-Mead * Starting Point: [1.0,0.2] * Minimizer: [1.8818299027162517,0.7002244825046421] * Minimum: 5.381270e-02 * Iterations: 34 * Convergence: true * √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true * Reached Maximum Number of Iterations: false * Objective Calls: 71

 P = Optim.minimizer(res2) Y = [ F(P, x) for x in xdata] using Plots plotly() plot(xdata, ydata) plot!(xdata, Y)

Bono Crea tu función de prueba

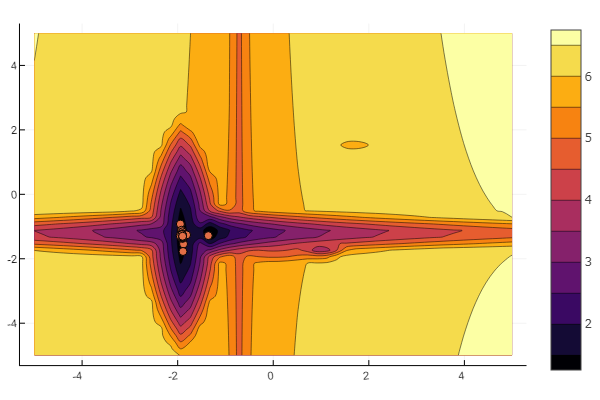
La idea se utiliza del artículo Khabrov . Puede configurar cada mínimo local usted mismo:

 """ https://habr.com/ru/post/349660/ :param n:   :param a:    ,   ,    /      :param c:    :param p:       :param b:    :return:  ,       ,          """ function feldbaum(x; n=5, a=[3 2; 4 3; 2 1; 4 5; .5 .5], c=[-1 2; 2 1; -3 2; -2 -2; 1.5 -2], p=[9 6; 1 1; 1.5 1.4; 1.2 1.3; 0.5 0.5], b=[0 1 3.2 2 4.6]) l = zeros(n) for i = 1:n res = 0 for j = 1:size(x,1) res += a[i,j] * abs(x[j] - c[i,j]) ^ p[i,j] end res += b[i] l[i] = res end minimum(l) end

Y puedes dejar todo a voluntad del todopoderoso al azar

 n=10 m = 2 a = rand(0:0.1:6, n, m) c = rand(-2:0.1:2, n, m) p = rand(0:0.1:2, n, m) b = rand(0:0.1:8, n, m) function feldbaum(x) l = zeros(n) for i = 1:n res = 0 for j = 1:m res += a[i,j] * abs(x[j] - c[i,j]) ^ p[i,j] end res += b[i] l[i] = res end minimum(l) end

Pero como puede ver en la imagen inicial, un enjambre de partículas con tal alivio no es intimidante.

Esto debería hacerse. Como puede ver, Julia tiene un entorno matemático bastante potente y moderno que permite estudios numéricos complejos sin rebajarse a las abstracciones de programación de bajo nivel. Y esta es una excelente ocasión para seguir estudiando este idioma.

¡Buena suerte a todos!