En este artículo, presento una nueva secuencia cuasialeatoria de baja divergencia que proporciona una mejora significativa sobre las secuencias modernas, como Sable, Niederreiter, etc.Figura 1. Comparación de varias secuencias cuasialeatorias con una divergencia baja. Tenga en cuenta que la propuesta por mí R -secuencia crea puntos distribuidos más uniformemente que todos los demás métodos. Además, todos los demás métodos requieren una cuidadosa selección de parámetros básicos, y en el caso de una selección incorrecta conducen a la degeneración (por ejemplo, en la esquina superior derecha)Temas cubiertos en este artículo- Secuencias de baja divergencia en una dimensión
- Métodos de baja divergencia en dos dimensiones.
- Distancia de embalaje
- Conjuntos multiclase de baja discrepancia
- Secuencias cuasialeatorias en la superficie de una esfera.
- Mosaico de plano cuasiperiódico
- Tramado de máscaras en gráficos por computadora
Hace algún tiempo, esta publicación fue publicada en la página de inicio de Hacker News. Puedes leer su
discusión allí .
Introducción: aleatorio versus cuasialeatorio
En la Figura 1, puede observar que con un muestreo aleatorio uniforme simple de un punto dentro de un cuadrado unitario, se observa una acumulación de puntos y también surgen áreas sin puntos ("ruido blanco"). Una
secuencia cuasialeatoria de
baja divergencia es un método de construcción (infinita) de puntos consecutivos de manera determinista, que reduce la probabilidad de acumulación (divergencia), al tiempo que garantiza una cobertura uniforme de todo el espacio ("ruido azul").
Secuencias cuasialeativas en una dimensión
Los métodos para crear secuencias cuasialeatorias completamente determinadas con baja divergencia en una dimensión están muy bien estudiados y resueltos en términos generales. En esta publicación, consideraré principalmente secuencias abiertas (infinitas), primero en una dimensión, y luego pasaré a dimensiones más altas. La ventaja fundamental de las secuencias abiertas (es decir, extensible en
n ) radica en el hecho de que si los errores totales basados en un número finito de miembros son demasiado grandes, entonces la secuencia puede expandirse sin descartar todos los puntos calculados anteriores. Hay muchas formas de construir secuencias abiertas. Puede dividir diferentes tipos en categorías por el método de construir sus parámetros básicos (hiper):
- fracciones irracionales: Kronecker, Richtmayer, Ramshaw
- (mutuamente) números primos: Van der Corpute, Holton, Foret
- Polinomios irreducibles: Niederreiter
- Polinomios primitivos: Sable
En aras de la brevedad, en esta publicación compararé principalmente el nuevo aditivo
recursivo R - una secuencia que pertenece a la primera categoría, es decir, a métodos recursivos basados en números irracionales (a menudo llamados secuencias de Kronecker,
Weil o Richtmeier), que son redes de rango 1, y una secuencia de Holton, que se basa en la secuencia unidimensional van der Corpute canónica. La secuencia recursiva canónica de Kronecker se define como:
R_1 (\ alpha): \; \; t_n = \ {s_0 + n \ alpha \}, \ quad n = 1,2,3, ...
donde
a l p h a - Cualquier número irracional. Tenga en cuenta que la entrada
\ {x \} denota la parte fraccional
x . En los cálculos, esta función a menudo se expresa como
R 1 ( a l p h a ) : t n = s 0 + n a l p h a ( t e x t r m m o d 1 ) ; q u un d n = 1 , 2 , 3 , . . .
En
s0=0 primeros miembros de la secuencia
R( phi) igual a:
tn=0.618,0.236,0.854,0.472,0,090,0,708,0.327,0.944,0.562,0.180,798,416,0,034,0,652,0.271,0,888,...
Es importante tener en cuenta que el significado
s0 no afecta las características generales de la secuencia, y en casi todos los casos es igual a cero. Sin embargo, al calcular la opción
s neq0 proporciona un grado adicional de libertad, que a menudo es útil. Si
s neq0 , entonces la secuencia a menudo se llama la "secuencia reticular desplazada". A pesar de que por defecto
s=0 Creo que hay consideraciones teóricas y prácticas para las cuales el valor debería ser estándar.
s=1/2 . Valor
alpha dando la menor discrepancia posible si
alpha=1/ phi donde
phi - Esta es la proporción áurea. Eso es
phi equiv frac sqrt5+12 simeq1.61803398875...;$
Es interesante notar que hay un número infinito de otros valores.
alpha , que también nos permiten obtener la discrepancia óptima, y todos están relacionados entre sí por la transformación de Mobius
alpha′= fracp alpha+qr alpha+s quad textrmparatodoslosenterosp,q,r,s quad textrmtalque|ps−qr|=1
Ahora comparamos este método recursivo con las conocidas secuencias de van der Korput con el orden inverso de las descargas [
van der Korput, 1935 ]. Las secuencias de Van der Corpute son en realidad una familia de secuencias, cada una de las cuales está definida por un hiperparámetro único
b . Los primeros miembros de la secuencia con b = 2 son iguales:
t[2]n= frac12, frac14, frac34, frac18, frac58, frac38, frac78, frac116, frac916, frac516, frac1316, frac316, frac1116, frac716, frac1516,...
En la siguiente sección, comparamos las características generales y la efectividad de cada una de estas secuencias. Considere el problema de calcular cierta integral
A= int10f(x) textrmdx
Podemos aproximarlo como:
A simeqAn= frac1n sumni=1f(xi), quadxi in[0,1]
- Si \ {x_i \} son iguales i/n , esta es la fórmula de los rectángulos ;
- Si \ {x_i \} seleccionado al azar, entonces este es el método de Monte Carlo ; pero
- Si \ {x_i \} son elementos de una secuencia con una divergencia baja, entonces este es el método cuasi-Monte Carlo .
El siguiente gráfico muestra curvas de error típicas.
sn=|A−An| para aproximar una cierta integral asociada con esta función,
f(x)= textrmexp( frac−x22),x en[0,1] para: (i) puntos cuasialeatorios de recursividad aditiva, donde
alpha=1/ phi , (azul) (ii) puntos cuasialeatorios de la secuencia de van der Corput, (naranja); (iii) puntos seleccionados al azar, (verde); (iv) Secuencias de Sable (rojo).
Esto muestra que para
n=106 La solución de puntos con muestreo aleatorio conduce a un error
simeq10−4 , la secuencia de van der Corput conduce a un error
simeq10−6 mientras que
R( phi) - la secuencia conduce a un error
simeq10−7 que en
sim 10 veces mejor que el error de van der Corput y
sim 1000 veces mejor que el muestreo aleatorio (uniforme).
Figura 2. Comparación de la integración numérica unidimensional utilizando varios métodos de Monte Carlo cuasialeatorios. Cuanto menor sea el valor, mejor. Nuevo R2 - la secuencia (azul) y la secuencia de Sable (rojo) son obviamente las mejores.Vale la pena mencionar lo siguiente:
- esto corresponde al conocimiento de que los errores para el muestreo aleatorio uniforme asintóticamente disminuyen a 1/ sqrtn , y el error para ambas secuencias cuasialeatorias tiende a 1/n .
- Resultados para R1( phi) -secuencias (azul) y secuencias Sable (rojo) son las mejores.
- ¡El gráfico demuestra que la secuencia de van der Corpute proporciona resultados buenos, pero increíblemente consistentes para las tareas de integración!
- Se puede ver aquí que para todos los valores n secuencia R1( phi) produce mejores resultados que la secuencia de van der Corput.
Nueva secuencia R1 , que es la secuencia de Kronecker que utiliza la proporción áurea, es una de las mejores opciones para los métodos de integración cuasirandom Monte Carlo unidimensionales (Quasirandom Monte Carlo, QMC).
También vale la pena señalar que aunque
alpha= phi teóricamente proporciona una opción demostrablemente óptima,
sqrt2 muy cerca de lo óptimo, y casi cualquier otro valor irracional
alpha proporciona curvas de error superiores para la integración unidimensional. Por eso se usa con mucha frecuencia.
alpha= sqrtp para cualquier número primo Además, desde el punto de vista de los cálculos, el valor aleatorio seleccionado en el intervalo
alpha en[0,1] es casi seguro (dentro de los límites de la precisión de la máquina) un número irracional y, por lo tanto, es una buena opción para una secuencia con poca divergencia. Para la legibilidad visual, la figura anterior no muestra los resultados de la secuencia de Niederreiter, porque son prácticamente indistinguibles de los resultados de las secuencias de Sobol y
R . Las secuencias de Niederreiter y Sable (junto con su selección de parámetros optimizada) que se utilizaron en esta publicación se calcularon en Mathematica utilizando lo que se denomina "generadores patentados cerrados y totalmente optimizados de la biblioteca Intel MKL" en la documentación.
Secuencias cuasialeatorias en dos dimensiones.
La mayoría de los métodos modernos para construir una varianza baja en dimensiones superiores simplemente se combinan (componente por componente)
d secuencias unidimensionales. Por brevedad, en la publicación consideraremos principalmente la secuencia de
Holton [
Holton, 1960 ], la secuencia de Sable y
d secuencia de Kronecker tridimensional.
La secuencia de Holton se construye usando simples
d varias secuencias unidimensionales de van der Corpute, cuya base es mutuamente simple para todos los demás. Es decir, son números coprimos por pares. Sin duda, la opción más común debido a su obvia simplicidad y lógica es la elección de la primera
d números primos La distribución de los primeros 625 puntos definidos por la secuencia de Holton (2,3) se muestra en la Figura 1. Aunque muchas secuencias de Holton bidimensionales son excelentes fuentes de secuencias con baja divergencia, es bien sabido que muchas de ellas son muy problemáticas y no presentan poca divergencia. Por ejemplo, la Figura 3 muestra que la secuencia de Holton (11,13) genera líneas muy notables. Se hicieron grandes esfuerzos para desarrollar métodos para seleccionar modelos y pares problemáticos.
(p1,p2) . En dimensiones superiores, el problema se vuelve aún más complicado.
Al generalizar a dimensiones superiores, los métodos recursivos de Kronecker sufren dificultades aún mayores. Aunque usando
alpha= sqrtp Se crean excelentes secuencias unidimensionales, ¡es extremadamente difícil incluso encontrar pares de primos que puedan usarse como base para un caso bidimensional
que no sea problemático! Se sugirió utilizar otros números irracionales conocidos como solución alternativa, por ejemplo
phi, pi,e,... . Proporcionan resultados moderadamente aceptables, pero generalmente no se usan, porque generalmente no son tan buenos como una secuencia Holton seleccionada correctamente. Se están haciendo grandes esfuerzos para resolver estos problemas de degeneración.
Las soluciones propuestas utilizan saltar / quemar, saltar / adelgazar. Y para la codificación (codificación) de las secuencias finales, se utiliza otra técnica, a menudo utilizada para superar este problema. La codificación no se puede utilizar para crear una secuencia abierta (infinita) con poca divergencia.
Figura 3. La secuencia (11,13) -Holton obviamente no es una secuencia de baja divergencia (izquierda). Tampoco es una secuencia aditiva recursiva (11,13) (en el medio). Algunas secuencias recursivas aditivas bidimensionales que usan números irracionales bien conocidos son bastante buenas (derecha).Del mismo modo, a pesar de los resultados generalmente mejores de la secuencia de Sable, su complejidad y, lo que es más importante, la necesidad de una selección muy cuidadosa de hiperparámetros hace que no sea tan amigable.
Así que de nuevo, en
d medidas:
- las secuencias típicas de Kronecker requieren una elección d números irracionales linealmente independientes;
- La secuencia de Holton requiere d enteros primos mutuamente primarios; pero
- La secuencia de Sable requiere una elección d números de guía
Nueva secuencia Rd - el único d secuencia cuasialeatoria tridimensional con una divergencia baja, que no requiere la elección de parámetros básicos.
Generalización de la proporción áurea
tl; dr En esta parte hablaré sobre cómo construir una nueva clase
d secuencia abierta (infinita) dimensional con baja divergencia, que no requiere una elección de parámetros básicos, que tiene excelentes propiedades de baja divergencia.
Hay muchas formas de generalizar la secuencia de Fibonacci y / o la proporción áurea. El método propuesto a continuación para generalizar la
proporción áurea no
es nuevo [
Krchadinac, 2005 ]. Además, el polinomio característico está asociado con muchas áreas de álgebra, incluidos los
números de Perron y los
números de Piso-Vijayaraghavan . Sin embargo, la conexión explícita entre esta forma generalizada y la construcción de secuencias de alta dimensión con baja divergencia es nueva. Definimos una vista generalizada de la proporción áurea.
phid como una raíz positiva única
xd+1=x+1 . Es decir
Para
d=1 ,
phi1=1.61803398874989484820458683436563... , que es la proporción dorada canónica.
Para
d=2 ,
phi2=1.32471795724474602596090885447809... . Este valor a menudo se llama constante de plástico y tiene
propiedades hermosas (ver también
aquí ). Se supone que este valor es más probable que sea óptimo para el problema bidimensional correspondiente [
Hensley, 2002 ].
Para
d=3 ,
phi3=1.220744084605759475361685349108831...Para
d>3 , aunque las raíces de esta ecuación no tienen una forma algebraica cerrada, podemos obtener fácilmente una aproximación numérica ya sea por métodos estándar, por ejemplo, el método de Newton, o notando eso para la siguiente secuencia
Rd( phid) :
t0=t1=...=td=1;
tn+d+1=tn+1+tn, quad textrmparan=1,2,3,..
Esta secuencia particular de constantes
phid Fue nombrado en 1928 por el arquitecto y monje Hans van de Laan como "
números armónicos ". Estos significados especiales se pueden expresar de manera muy elegante de la siguiente manera:
phi1= sqrt1+ sqrt1+ sqrt1+ sqrt1+ sqrt1+...
phi2= sqrt[3]1+ sqrt[3]1+ sqrt[3]1+ sqrt[3]1+ sqrt[3]1+...$
phi3= sqrt[4]1+ sqrt[4]1+ sqrt[4]1+ sqrt[4]1+ sqrt[4]1+...$
También tenemos la siguiente propiedad muy elegante:
phid= limn to infty fractn+1tn
Esta secuencia, a veces llamada secuencia de Fibonacci generalizada o diferida, se ha estudiado bastante profundamente [
As, 2004 ,
Wilson, 1993 ], y la secuencia para
d=2 a menudo llamada la secuencia de Padovan [
Stuart, 1996 ,
OEIS A000931 ], y la secuencia
d=3 enumerados en [
OEIS A079398 ]. Como se indicó anteriormente, la tarea principal de esta publicación es describir la conexión explícita entre esta secuencia generalizada y la construcción
d tridimensionales con baja divergencia.
Resultado principal: el siguiente no paramétrico d secuencia abierta (infinita) tridimensional Rd( phid) tiene excelentes características de baja discrepancia en comparación con otros métodos existentes.
\ mathbf {t} _n = \ {n \ pmb {\ alpha} \}, \ quad n = 1,2,3, ...
textrmwhere quad pmb alpha=( frac1 phid, frac1 phi2d, frac1 phi3d,... fr a c 1 p h i d d )
textrmy phid textrmesunaraízpositivaúnicaxd+1=x+1
Para dos dimensiones, esta secuencia generalizada para
n=150 se muestra en la figura 1. Los puntos obviamente se distribuyen mucho más uniformemente en
R2 -secuencias que en (2, 3) -Holton secuencias, secuencias de Kronecker basadas en
( sqrt3, sqrt7) , Secuencias de Niederreiter y Sable. (Debido a la complejidad de las secuencias de Niederreiter y Sable, se calcularon en Mathematica utilizando un código propietario proporcionado por Intel). Este es el tipo de secuencia en la que el vector base
pmb alpha es una función de un solo valor de material, a menudo llamado la secuencia de Korobov [Korobov, 1959]
Mire nuevamente la Figura 1 para comparar varias secuencias cuasialeatorias de baja divergencia bidimensionales.Código y Demos
En una dimensión, seudocódigo para
n miembro (
n = 1,2,3, ....) se define como
g = 1.6180339887498948482 a1 = 1.0/g x[n] = (0.5+a1*n) %1
En dos dimensiones, el pseudocódigo para las coordenadas.
x y
yn miembro (
n = 1,2,3, ....) Se definen como
g = 1.32471795724474602596 a1 = 1.0/g a2 = 1.0/(g*g) x[n] = (0.5+a1*n) %1 y[n] = (0.5+a2*n) %1
Pseudocódigo en tres dimensiones para coordenadas
x ,
y y
zn miembro (
n = 1,2,3, ....) se define como
g = 1.22074408460575947536 a1 = 1.0/g a2 = 1.0/(g*g) a3 = 1.0/(g*g*g) x[n] = (0.5+a1*n) %1 y[n] = (0.5+a2*n) %1 z[n] = (0.5+a3*n) %1
Plantilla de código Python (¡tenga en cuenta que las matrices y bucles de Python comienzan desde cero!)
import numpy as np
Escribí el código de tal manera que correspondía a la notación matemática utilizada en esta publicación. Sin embargo, por razones de convenciones de programación y / o eficiencia, vale la pena mencionar algunas modificaciones. Primero, desde
R2 es una secuencia
recursiva aditiva, formulación alternativa
z que no requiere multiplicación de punto flotante y mantiene una alta precisión para muy grandes
n tiene la forma
z[i+1] = (z[i]+alpha) %1
En segundo lugar, en lenguajes que pueden vectorizarse, el código de una función fraccional se puede vectorizar de la siguiente manera:
for i in range(n): z[i] = seed + alpha*(i+1) z = z %1
Finalmente, podemos reemplazar estas adiciones de coma flotante y números enteros multiplicando todas las constantes por
232 , y luego cambiando la función frac (.) en consecuencia. Aquí están las demostraciones de código fuente creadas por otras personas basadas en esta secuencia:
Distancia mínima de embalaje
Nuevo R2 -secuencia es la única secuencia cuasialeatoria bidimensional con una divergencia baja en la que la distancia mínima de empaque se reduce solo a 1/ sqrtn .
Aunque el análisis técnico estándar del cálculo de discrepancia es
d∗ - discrepancias, primero mencionaremos un par de otras formas geométricas (¡y quizás mucho más intuitivas!) para demostrar cuánto es preferible la nueva secuencia a otros métodos estándar. Si denotamos la distancia entre puntos
i y
j para
dij y
d0= textrminfdij entonces el cuadro a continuación muestra cómo varía
d0(n) para
R -secuencias, (2,3) - secuencias de Holton, Sable, Niederreiter y secuencias aleatorias. Esto se puede ver en la Figura 6.
Como en la figura anterior, el valor de la distancia mínima está normalizado por el coeficiente
1/ sqrtn . Puede notar que después
n=300 puntos en una secuencia aleatoria (verde) casi con certeza aparecen dos puntos que están muy cerca uno del otro. También se ve que aunque la secuencia de Holton (2,3) es mucho mejor que el muestreo aleatorio, también, desafortunadamente, disminuye asintóticamente a cero. Para la secuencia de Sable, el motivo de la normalización disminuye a cero
d0 miente en el hecho de que el
mismo Sable demostró que
la secuencia de
Sable cae a una velocidad
/n - lo cual es bueno, pero obviamente mucho peor que
R2 que disminuye solo en
1/ sqrtn .
Por secuencia
R( phi2) (azul) la distancia mínima entre dos puntos cae constantemente en el intervalo de
0.549/ sqrtn antes
0.868/ sqrtn . Tenga en cuenta que el diámetro óptimo de 0.868 corresponde a un factor de empaque de 59.2%. Compare esto con otros
paquetes de círculos .
También tenga en cuenta que el
muestreo de disco de Bridson Poisson , que
no es expandible a
n y generalmente se recomienda por defecto, todavía crea un factor de empaque de 49.4%. Vale la pena considerar que el concepto
d0 secuencias fuertemente unidas
phid baja discrepancia con números / vectores poco aproximables en
d mediciones [
Hensley, 2001 ]. Aunque sabemos poco sobre números poco aproximados en dos dimensiones, la construcción
phid puede proporcionarnos una nueva mirada a números poco aproximados en dimensiones superiores.
Figura 4. Distancia mínima por pares para varias secuencias con baja divergencia. Tenga en cuenta que R2 - la secuencia (azul) es siempre la mejor opción; Además, esta es la única secuencia en la que la distancia normalizada no tiende a cero en n rightarrow infty . La secuencia de Holton (naranja) ocupa el segundo lugar, y las secuencias de Sable (verde) y Niederreiter (rojo) no son tan buenas, pero aún son mucho mejores que las aleatorias (púrpura). Cuanto más grande, mejor, porque esto corresponde a una distancia de embalaje más larga.Diagramas de Voronoi
Otra forma de visualizar la distribución uniforme de puntos es crear un diagrama de Voronoi desde el primer
n puntos de una secuencia bidimensional con color posterior de cada área dependiendo de su
área . La siguiente figura muestra las tablas de colores de Voronoi para (i)
R2 -secuencias; (ii) (2,3) secuencias de Holton, (iii) recursividad primaria; y (iv) muestreo aleatorio simple. Para todas las figuras se usa la misma escala de colores. Aquí de nuevo, es obvio que
R2 La secuencia proporciona una distribución mucho más uniforme que la secuencia de Holton o el muestreo aleatorio simple. La imagen es la misma que la anterior, solo coloreada de acuerdo con el número de vértices en cada celda Voronoi. Aquí no solo es obvio que
R - la secuencia proporciona una distribución más uniforme que Holton o muestreo aleatorio simple, pero el hecho de que los valores clave son más notables
n consisten en solo hexágonos! Si consideramos la secuencia de Fibonacci generalizada, entonces
A1=A2=A3=1; quadAn+3=An+1+An . Eso es
An :
$$ display $$ \ begin {array} {r} 1 y 1 y 1 y 2 y 2 y 3 y 4 y 5 y 7 \\ 9 y \ textbf {12} y 16 y 21 y 28 y 37 y \ textbf {49} y 65 y 86 \\ 114 y \ textbf {151 } Y 200 y 265 y 351 y 465 y \ textbf {616} y 816 y 1081 \\ 1432 y \ textbf {1897} y 2513 y 3329 y 4410 y 5842 y \ textbf {7739} y 10252 y 13581 \\ 17991 y \ textbf {23833} y 31572 y 41824 y 55405 {97229} y 128801 y 170625 \\ 226030 & \ textbf {299426} y 396655 y 525456 y 696081 y 922111 y \ textbf {1221537} y 1618192 y 2143648 \\ \ end {array} $$ display $$
Todos los valores en los que
n=A9k−2 o
n=A9k+2 consisten solo en hexágonos.
Figura 4. Visualización de la forma de los diagramas de Voronoi en función del área de cada polígono de Voronoi para (i) R2 -secuencias; (ii) secuencias (2,3) basadas en números primos; (iii) la secuencia (2,3) de Holton, (iv) Niederraiter; (v) Sable; y (iv) muestreo aleatorio simple. Los colores indican el número de lados de cada polígono Voronoi. Repito: es obvio que R( phi) -secuencia proporciona una distribución mucho más uniforme que cualquier otra secuencia con una divergencia baja.A ciertos valores n Rejilla Voronoi para R2 -la secuencia consta solo de hexágonos.
Figura 5. Visualización de la forma de los diagramas de Voronoi en función del número de lados de cada polígono de Voronoi para (i) R2 -secuencias; (ii) secuencias (2,3) basadas en números primos; (iii) la secuencia (2,3) de Holton, (iv) Niederraiter; (v) Sable; y (iv) muestreo aleatorio simple. Los colores indican el número de lados de cada polígono Voronoi. Repito: es obvio que R( phi) -secuencia proporciona una distribución mucho más uniforme que cualquier otra secuencia con una divergencia baja.Mosaico cuasialeatorio de Delaunay para un avión
R -secuencia es la única secuencia cuasialeatoria de baja divergencia que se puede utilizar para crear d tridimensionales cuasiperiódicas utilizando su malla Delaunay.
La triangulación de Delaunay, que es similar al Conde Voronoi, brinda la oportunidad de ver estas distribuciones de manera diferente. Sin embargo, lo que es más importante, la triangulación de Delaunay proporciona un nuevo método para crear mosaico cuasiperiódico (mosaico) de un plano. Triangulación de Delaunay
R2 -secuencias proporciona un patrón mucho más uniforme que una secuencia de Holton o un muestreo aleatorio. En particular, si se realiza la triangulación de Delaunay de distribuciones de puntos, donde
n igual a cualquiera de la secuencia de Fibonacci generalizada:
AN=$1,1,1,2,3,4,5,7,9,12,16,21,28,37,... , entonces la triangulación de Delaunay consta de solo tres triángulos idénticamente emparejados, es decir, de paralelogramos (romboides). (Excepto los triángulos que tienen un vértice común con un casco convexo). Además,
En valores n=Ak Triangulación de Delaunay R2 -secuencias forma inclinaciones cuasiperiódicas, cada una de las cuales consta de solo tres triángulos básicos (rojo, amarillo, azul), que siempre están conectados en pares y forman un mosaico cuasiperiódico (mosaico) bien definido del plano con tres paralelogramos (romboides).
Figura 6. Visualización de la triangulación de Delaunay para (i) R( phi2) -secuencias; (ii) (2,3) secuencias de Holton, (iii) recursividad primaria; y (iv) muestreo aleatorio simple. Los colores indican el área de cada triángulo. Los cuatro gráficos usan la misma escala. Y aquí de nuevo es obvio que R( phi2) -secuencia proporciona una distribución mucho más uniforme que cualquier otra secuencia con una divergencia baja.Tenga en cuenta que
R2 basado en
phi2=1.32471795724474602596 siendo el menor número de piso, (a
phi=1.61803... Es el mayor número de pisos). La conexión del mosaico cuasiperiódico con los números cuadráticos y cúbicos de Piso no es nueva [
Elkharrat y Masakova], pero creo que por primera vez se creó el mosaico cuasiperiódico sobre la base de
phi2=1.324719... .
La animación a continuación muestra cómo la malla de Delaunay para la secuencia
R2 cambia con la adición gradual de puntos. Tenga en cuenta que cuando el número de puntos es igual a un miembro de la secuencia generalizada de Fibonacci, entonces toda la cuadrícula de Delaunay consiste solo en paralelogramos rojos, azules y amarillos (romboides), dispuestos en una doble forma cuasiperiódica.
Aunque la disposición de los paralelogramos rojos demuestra una regularidad considerable, se puede ver claramente que los paralelogramos azules y amarillos se colocan en forma cuasiperiódica. El espectro de Fourier de esta red se puede ver en la Figura 11; representa los espectros de puntos clásicos. (Tenga en cuenta que una secuencia recursiva basada en primos también parece cuasiperiódica en el sentido de que es un patrón ordenado no repetitivo. Sin embargo, su patrón en el intervalo
n no tan constante, y también depende críticamente de la elección de parámetros básicos. Por lo tanto, enfocaremos nuestro interés en las inclinaciones cuasiperiódicas solo por la secuencia
R2 .) Se compone de solo tres triángulos: rojo, amarillo, azul. Tenga en cuenta que en esta secuencia
R( phi2) Todos los paralelogramos de cada color tienen el mismo tamaño y forma. La relación de aspecto de estos triángulos individuales es increíblemente elegante. A saber
textrmÁrea(rojo):Área(amarillo):Área(azul)=1: phi2: phi22
Lo mismo se aplica a la frecuencia relativa de los triángulos:
f( textrmrojo):f( textrmamarillo):f( textrmazul)=1: phi2:1
De esto se deduce que el área relativa total cubierta por estos tres triángulos en el espacio es:
f( textrmrojo):f( textrmamarillo):f( textrmazul)=1: phi22: phi22
También se puede suponer que podemos crear este mosaico cuasiperiódico a través de la sustitución basada en la secuencia A. Eso es
A rightarrowB; quadB rightarrowC; quadC rightarrowBA
Para tres dimensiones, si consideramos la secuencia de Fibonacci generalizada, entonces
B1=B2=B3=B4=1; quadBn+4=Bn+1+Bn . Eso es
B_n = \ {1,1,1,1,2,2,2,3,4,4,5,7,8,9,12,15,17,21,27,32,38,48,59 , 70,86,107,129, ...
A ciertos valores n=Bk Malla 3D Delaunay asociada a una secuencia R3 , define una red cristalina cuasiperiódica.
Embalaje discreto, parte 2
La siguiente figura muestra el primer
n=2500 puntos para cada secuencia bidimensional con baja divergencia. Además, cada una de las celdas 50 × 50 = 2500 se colorea de verde solo si contiene
exactamente 1 punto. Es decir, cuanto más cuadrados verdes, más uniforme es la distribución de 2500 puntos en 2500 celdas. El porcentaje de celdas verdes para cada una de las figuras es el siguiente:
R2 (75%), Holton (54%), Kronecker (48%), Niederreiter (54%), Sable (49%) y aleatorio (38%).
Ondas sonoras
Solo por diversión, a pedido de
un lector de News Hacker, modelé cómo pueden
sonar todas estas distribuciones de puntos cuasialeatorios. Usé la función Listplay de Mathematica: "
ListPlay [{a1, a2, ...}] crea un objeto que se reproduce como sonido, cuya amplitud se da como una secuencia de niveles". Por lo tanto, sin ningún comentario, te dejaré decidir por ti mismo cuáles te gustan más entre las distribuciones cuasialeativas unidimensionales (mono) y las distribuciones cuasialeatorias bidimensionales (estéreo).
| Mono | Estéreo |
|---|
| Al azar | | |
| Sable | | |
| Niederreiter | | |
| Holton | | |
| Kronecker | | |
| R | | |
Conjuntos multiclase de baja discrepancia
Algunas secuencias de baja divergencia demuestran lo que se llama una "divergencia baja de múltiples clases". Hasta este momento, asumimos que cuando necesitamos distribuir lo más uniformemente posible
n puntos, entonces todos los puntos son iguales e indistinguibles entre sí. Sin embargo, en muchas situaciones, hay diferentes tipos de puntos. Consideramos el problema de la distribución uniforme.
n para que no solo todos los puntos se distribuyan de manera uniforme, sino también puntos de la misma clase. En particular, supongamos que hay
nk puntos de tipo
k , (donde
n1+n2+n3+...+nk=n ), entonces la distribución del conjunto múltiple con una distribución baja es una distribución en la que cada
nk puntos distribuidos uniformemente. En nuestro caso, encontramos que
R -La secuencia y secuencia de Holton es fácil de adaptar a secuencias de múltiples conjuntos con poca divergencia, simplemente colocando puntos alternativos de cada tipo.
La figura a continuación muestra cómo se distribuyen
n=150 puntos, mientras que 75 son azules, 40 son picantes, 25 son verdes y 10 son rojos. Para una secuencia recursiva aditiva, esto se resuelve trivialmente: los primeros 75 miembros simplemente corresponden al azul, los siguientes 40 al naranja, los siguientes 25 al verde y los últimos 10 a los puntos rojos. Esta técnica casi funciona para las secuencias de Holton y Kronecker, pero funciona muy mal en las secuencias de Niederreiter y Sable. Además, no existen técnicas conocidas para la generación continua de distribuciones puntuales de múltiples escalas en las secuencias de Niederreiter y Sable. Esto muestra que las
distribuciones de puntos multiclase , por ejemplo, como los
ojos de los pollos , ahora se pueden describir y construir directamente usando secuencias con poca divergencia.
Secuencia R2 Es una secuencia cuasialeatoria de baja divergencia que proporciona una construcción fácil de una divergencia baja de múltiples clases.
Figura 9. Secuencias multiescala con baja divergencia. En secuencia R no solo todos los puntos están distribuidos uniformemente, sino también los puntos de cada color individual.Puntos cuasialeatorios en una esfera
En los campos de los gráficos por computadora y la física, a menudo es necesario distribuir puntos en la superficie de una esfera tridimensional de la manera más uniforme posible. Cuando se utilizan secuencias cuasialeativas abiertas (infinitas), este problema se reduce solo a la colocación de puntos cuasialeatorios distribuidos uniformemente en un cuadrado unitario en la superficie de la esfera utilizando la proyección igual de Lambert. Transformación de proyección estándar de Lambert colocando un punto
(u,v) enU[0,1] a(x,y,z) enS2 tiene la forma:
(x,y,z)=( cos lambda cos phi, cos lambda sin phi, sin lambda)
textrmdonde quad cos( lambda− pi/2)=(2u−1); quad phi=2 piv
Ya que esto
phi2 -la secuencia está completamente abierta, le permite ajustar una secuencia infinita de puntos a la superficie de la esfera, un punto a la vez. Esto contrasta con otros métodos, como la
red de la espiral de Fibonacci , que requieren conocer el número de puntos de antemano. En la inspección visual, nuevamente podemos ver claramente que
n=1200 nuevo
R( phi2) - La secuencia está mucho mejor distribuida que la superposición de Holton o el muestreo de Kronecker, que, a su vez, es mucho más uniforme que el muestreo aleatorio.
Figura 10Dithering de gráficos por computadora
La mayoría de las técnicas modernas de dithering (por ejemplo, el dithering de Floyd-Steinberg) se basan en la distribución de errores, que no es muy adecuada para el procesamiento paralelo y / o la optimización directa en la GPU. En tales casos, el dithering con máscaras de dither estático (es decir, completamente dependientes de la imagen objetivo) muestra excelentes características de rendimiento. Probablemente las máscaras de difuminado más famosas y ampliamente utilizadas se basan en matrices
Bayer , pero las más nuevas intentan simular las características del ruido azul más cerca. La dificultad no trivial de crear máscaras de oscilación basadas en secuencias de baja divergencia y / o ruido azul es que estas secuencias de baja divergencia proyectan un número entero
Z a un punto bidimensional en el intervalo
[0,1)2 .
Pero para una máscara de tramado, se requiere una función que proyecte las coordenadas enteras bidimensionales de la máscara rasterizada en un valor de brillo / umbral real en el intervalo [0,1) .
Sugiero el siguiente enfoque basado en R-secuencias. Para cada píxel (x, y) en la máscara, asignamos su valor de brilloI(x,y) donde:I(x,y)=α1x+α2y(mod1);
αα=(α1,α2)=(1ϕ2,1ϕ22)
ϕ2 - x3=x+1
Eso es x=1.32471795724474602596… lo que significaα1=0.75487766624669276;α2=0.569840290998
Además, si se agrega una función de onda triangular para eliminar la discontinuidad causada por la función frac (.) En cada límite entero:T(z)={2z,if 0≤z<1/22−2z,if1/2≤z<1
I(x,y)=T[α1x+α2y(mod1)];
entonces la máscara y su diagrama de Fourier / frecuencia se mejoran aún más. También notamos que desdelimn→∞AnAn+1=0.754878;limn→∞AnAn+2=0.56984
entonces la forma de la expresión anterior está relacionada con la siguiente ecuación congruenteAnx+An+1y(modAn+2) for integers x,y
Las máscaras R difuminadas crean resultados que compiten con los métodos modernos basados en máscaras de ruido azul. Pero a diferencia de las máscaras de ruido azul, no es necesario calcularlas de antemano, ya que pueden calcularse en tiempo real.
Vale la pena señalar que Mittring también propuso esta estructura , pero encuentra los coeficientes empíricamente (y no reproduce los valores finales). Además, ayuda a comprender por qué la fórmula empírica de Jorge Jiménez para crear "Call of Duty" (a menudo llamada "Ruido de gradiente intercalado") funciona tan bien .I(x,y)=(FractionalPart[52.9829189∗FractionalPart[0.06711056∗x+0.00583715∗y]]
Sin embargo, requiere 3 multiplicaciones de punto flotante y dos operadores% 1, y la fórmula anterior muestra que podemos hacer esto con solo dos multiplicaciones de punto flotante y una operación% 1. Pero lo más importante, esta publicación proporciona una comprensión matemática más clara de por qué una máscara de oscilación en esta forma es tan efectiva, si no óptima. Los resultados de esta matriz de dithering se muestran a continuación utilizando la imagen de prueba clásica Lena 256 × 256, así como un patrón de prueba de ajedrez como ejemplo. También muestra los resultados del uso de máscaras de difuminado estándar de Bayer, así como un ejemplo con ruido azul. Los dos métodos más comunes de ruido azul son Void-and-Cluster y Poisson disc sample. Para abreviar, solo he mostrado los resultados del método Void y cluster. [ Peters] El ruido degradado intercalado funciona mejor que Bayer y el ruido azul, pero no tan bueno comoRvacilante Puede ver que el tramado de Bayer muestra una notable disonancia del blanco en las áreas de color gris claro. TramadoR- la secuencia y el ruido azul son generalmente comparables, aunque pueden distinguirse pequeñas diferencias. Vale la pena señalar algunos aspectos de R-dithering:- ¡Él no es isotrópico! Los espectros de Fourier muestran solo puntos individuales y discretos. Esta es una característica clásica de las inclinaciones cuasiperiódicas y los espectros de difracción de cuasicristales. En particular, los espectros de Fourier paraR Las máscaras corresponden al hecho de que la triangulación de Delaunay para la secuencia R canónica consiste en un mosaico cuasiperiódico de tres paralelogramos.
- ¡El tramado R cuando se combina con una onda triangular proporciona una máscara increíblemente uniforme!
- R- , .
- , , R- , .
- (I(x,y) , .
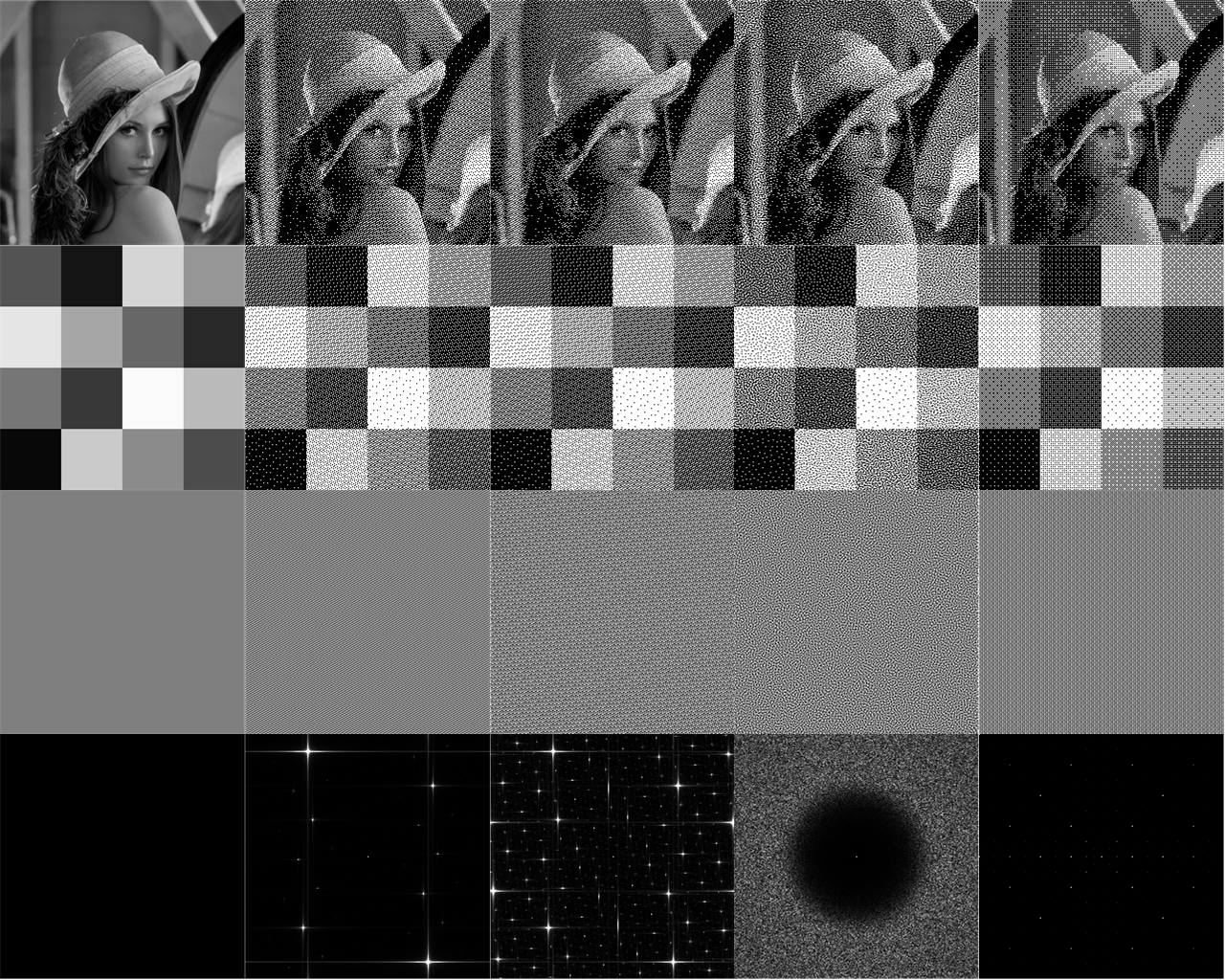
Mayores dimensiones
Similar a la sección anterior, pero para cinco (5) mediciones, el siguiente gráfico muestra la distancia mínima (global) entre dos puntos para R(ϕ5)-secuencias, (2,3,5,7,11) -Holton secuencias y secuencias aleatorias. Esta vez, el valor normalizado de la distancia mínima se normaliza por un factor1/5√n .
Puede ver que, debido a la "maldición de las dimensiones", la distribución aleatoria es mejor que todas las secuencias con poca divergencia, con la excepción de R5-secuencias. EnR(ϕ5) -secuencias incluso con n≃106 puntos, la distancia mínima entre dos puntos todavía está constantemente cerca 0.8/√n y siempre más alto 0.631/√n .
Secuencia R2 - el único d secuencia tridimensional con baja divergencia, en la cual la distancia de empaque comienza a caer solo con la velocidad n−1/d .
Figura 12. Esto muestra que la secuencia R (azul) es consistentemente mejor que Holton (naranja); Sable (verde); Niederreiter (rojo); y al azar (morado). Tenga en cuenta que cuanto más grande, mejor, porque esto corresponde a una distancia de embalaje más larga.Integración numérica
El siguiente gráfico muestra curvas de error típicas. sn=|A−An| para aproximar una cierta integral asociada con una función gaussiana de ancho medio σ=√d ,
f(x)=exp(−x22d),x∈[0,1] , mientras que: (i) Rϕ(azul); (ii) secuencia de Holton (naranja); (iii) aleatorio (verde); (iv) Sable (rojo). El gráfico muestra que paran=106Ahora hay menos diferencias entre el muestreo aleatorio y la secuencia de Holton. Sin embargo, como se mostró en el caso unidimensional,R- Secuencia y Sable siempre son mejores que la secuencia de Holton. También nos permite saber que la secuencia de Sable es ligeramente mejor.R -secuencias.Figura 13. Métodos cuasialeatorios de Monte Carlo para la integración de 8 dimensiones. Cuanto menor sea el valor, mejor. La nueva secuencia R y la secuencia Sable se muestran mucho mejor que la secuencia Holton.