🕕 💷 🛌🏽 Programación relacional: dolor, interés y dolor de nuevo. 👨🏾‍🤝‍👨🏻 🏌️ 🎃

En la publicación anterior contamos en detalle lo que enseñamos a los estudiantes en el campo de la "Programación industrial". Para aquellos cuyo área de interés se encuentra en un campo más teórico, por ejemplo, atraídos por los nuevos paradigmas de programación o las matemáticas abstractas utilizadas en la investigación teórica sobre programación, existe otra especialización: "Lenguajes de programación".

Hoy hablaré sobre mi investigación en el campo de la programación relacional, que hago en la universidad y como estudiante investigadora en el laboratorio de herramientas de lenguaje JetBrains Research.

¿Qué es la programación relacional? Usualmente ejecutamos una función con argumentos y obtenemos el resultado. Y en el caso relacional, puede hacer lo contrario: arreglar el resultado y un argumento, y obtener el segundo argumento. Lo principal es escribir el código correctamente y ser paciente y tener un buen clúster.

Sobre mi

Mi nombre es Dmitry Rozplokhas, soy estudiante de primer año del HSE de San Petersburgo, y el año pasado me gradué del programa de licenciatura de la Universidad Académica en el campo de "Lenguajes de programación". Desde el tercer año de estudios de pregrado, también soy estudiante de investigación en el laboratorio de herramientas lingüísticas de JetBrains Research.

Programación relacional

Hechos generales

La programación relacional es cuando, en lugar de funciones, usted describe la relación entre argumentos y el resultado. Si el lenguaje se agudiza para esto, puede obtener ciertas bonificaciones, por ejemplo, la capacidad de ejecutar la función en la dirección opuesta (como resultado, restaurar los posibles valores de los argumentos).

En general, esto se puede hacer en cualquier lenguaje lógico, pero el interés en la programación relacional surgió simultáneamente con el advenimiento de un miniKanren de lenguaje lógico puro minimalista hace unos diez años, que hizo posible describir y usar convenientemente tales relaciones.

Estos son algunos de los casos de uso más avanzados: puede escribir un comprobador de pruebas y usarlo para encontrar evidencia ( Near et al., 2008 ) o crear un intérprete para algún lenguaje y usarlo para generar programas de pruebas ( Byrd et al., 2017 ).

Ejemplo de sintaxis y juguete

miniKanren es un lenguaje pequeño; solo se utilizan construcciones matemáticas básicas para describir las relaciones. Este es un lenguaje incrustado, sus primitivas son una biblioteca para algún lenguaje externo, y se pueden usar pequeños programas miniKanren dentro de un programa en otro idioma.

Idiomas extranjeros adecuados para miniKanren, un montón. Inicialmente, estaba Scheme, estamos trabajando con la versión para Ocaml ( OCanren ), y la lista completa se puede ver en minikanren.org . Los ejemplos en este artículo también estarán en OCanren. Muchas implementaciones agregan funciones auxiliares, pero nos centraremos solo en el lenguaje central.

Comencemos con los tipos de datos. Convencionalmente, se pueden dividir en dos tipos:

Las constantes son algunos datos del idioma en el que estamos incrustados. Cadenas, números, incluso matrices. Pero para el miniKanren básico, todo esto es un cuadro negro, las constantes solo se pueden verificar para la igualdad.
Un "término" es una tupla de varios elementos. Comúnmente utilizado de la misma manera que los constructores de datos en Haskell: constructor de datos (cadena) más cero o más parámetros. OCanren utiliza constructores de datos regulares de OCaml.

Por ejemplo, si queremos trabajar con matrices en miniKanren, entonces debe describirse en términos de términos similares a los lenguajes funcionales, como una lista individualmente vinculada. Una lista es una lista vacía (indicada por un término simple) o un par del primer elemento de la lista ("encabezado") y otros elementos ("cola").

let emptyList = Nil let list_123 = Cons (1, Cons (2, Cons (3, Nil)))

Un programa miniKanren es la relación entre algunas variables. Al inicio, el programa proporciona todos los valores posibles de las variables en forma general. A menudo, las implementaciones le permiten limitar el número de respuestas en la salida, por ejemplo, encontrar solo la primera; la búsqueda no siempre se detiene después de encontrar todas las soluciones.

Puede escribir varias relaciones que se definen entre sí e incluso se llaman recursivamente como funciones. Por ejemplo, a continuación, en lugar de la función

a p p e n d (a, b) \to c o n

$append (a, b) → con$ define la relación

a p p e n d o (a, b, c)

$appendo (a, b, c)$ : lista

c

$c$ es una concatenación de listas

a

$a$ y

b

$b$ . Las funciones que devuelven relaciones terminan tradicionalmente con una "o" para distinguirlas de las funciones ordinarias.

Una relación se escribe como una declaración con respecto a sus argumentos. Tenemos cuatro operaciones básicas :

Unificación o igualdad (===) de dos términos, los términos pueden incluir variables. Por ejemplo, puede escribir la relación "lista consta de un elemento ":
```
 let isSingletono xl = l === Cons (x, Nil) 
```
Conjunción (lógica "y") y disyunción (lógica "o"), como en la lógica ordinaria. Los OCanren se denominan &&& y |||. Pero básicamente no hay una negación lógica en MiniKanren.
Agregar nuevas variables. En lógica, es un cuantificador de la existencia. Por ejemplo, para verificar que la lista no esté vacía, debe verificar que la lista consta de una cabeza y una cola. No son argumentos de la relación, por lo que debe crear nuevas variables:
```
 let nonEmptyo l = fresh (ht) (l === Cons (h, t)) 
```

Una relación puede invocarse de forma recursiva. Por ejemplo, debe definir el elemento "relación"

x

$x$ se encuentra en la lista ". Resolveremos este problema analizando casos triviales, como en los lenguajes funcionales:

O el jefe de la lista es $x$
Ya sea $x$ se encuentra en la cola

 let membero lx = fresh (ht) ( (l === Cons (h, t)) &&& (x === h ||| membero tx) )

La versión básica del lenguaje se basa en estas cuatro operaciones. También hay extensiones que le permiten usar otras operaciones. El más útil de ellos es la restricción de desigualdad para establecer la desigualdad de dos términos (= / =).

A pesar del minimalismo, miniKanren es un lenguaje bastante expresivo. Por ejemplo, observe la concatenación relacional de dos listas. La función de dos argumentos se convierte en una triple relación "

a b

$ab$ es una concatenación de listas

a

$a$ y

b

$b$ ".

 let appendo ab ab = (a === Nil &&& ab === b) ||| (fresh (ht tb) (*  :  fresh   &&& *) (a = Cons (h, t)) (appendo tb tb) (ab === Cons (h, tb)))

La solución no es estructuralmente diferente de cómo la escribiríamos en un lenguaje funcional. Analizamos dos casos unidos por una cláusula:

Si la primera lista está vacía, entonces la segunda lista y el resultado de la concatenación son iguales.
Si la primera lista no está vacía, la analizamos en la cabeza y la cola y construimos el resultado usando una llamada recursiva de la relación.

Podemos hacer una solicitud a esta relación, arreglando el primer y segundo argumento; obtenemos la concatenación de listas:

 run 1 (λ q -> appendo (Cons (1, Cons (2, Nil))) (Cons (3, Cons (4, Nil))) q)

⇒

 q = Cons (1, Cons (2, Cons (3, Cons (4, Nil))))

Podemos arreglar el último argumento: obtenemos todas las particiones de esta lista en dos.

 run 4 (λ qr -> appendo qr (Cons (1, Cons (2, Cons (3, Nil)))))

⇒

 q = Nil, r = Cons (1, Cons (2, Cons (3, Nil))) | q = Cons (1, Nil), r = Cons (2, Cons (3, Nil)) | q = Cons (1, Cons (2, Nil)), r = Cons (3, Nil) | q = Cons (1, Cons (2, Cons (3, Nil))), r = Nil

Puedes hacer cualquier otra cosa. Un ejemplo un poco más no estándar, en el que arreglamos solo parte de los argumentos:

 run 1 (λ qr -> appendo (Cons (1, Cons (q, Nil))) r (Cons (1, Cons (2, Cons (3, Cons (4, Nil))))))

⇒

 q = 2, r = Cons (3, Cons (4, Nil))

Como funciona

Desde el punto de vista de la teoría, aquí no hay nada impresionante: siempre puede comenzar a buscar todas las opciones posibles para todos los argumentos, verificando para cada conjunto si se comportan con respecto a una función / relación dada como nos gustaría (ver "Algoritmo del Museo Británico" ) . Es interesante el hecho de que aquí la búsqueda (en otras palabras, la búsqueda de una solución) utiliza solo la estructura de la relación descrita, por lo que puede ser relativamente efectiva en la práctica.

La búsqueda está relacionada con la acumulación de información sobre diversas variables en el estado actual. No sabemos nada acerca de cada variable, o sabemos cómo se expresa en términos, valores y otras variables. Por ejemplo:

b = Cons (x, y)
c = Cons (10, z)
x = ?
y = ?
z = ?

Al pasar por la unificación, observamos dos términos con esta información en mente y actualizamos el estado o finalizamos la búsqueda si dos términos no pueden unificarse. Por ejemplo, completando la unificación b = c, obtenemos nueva información: x = 10, y = z. Pero la unificación b = Nil causará una contradicción.

Buscamos en conjunciones secuencialmente (para que la información se acumule), y en una disyunción dividimos la búsqueda en dos ramas paralelas y avanzamos, alternando pasos en ellas: esta es la llamada búsqueda intercalada. Gracias a esta alternancia, la búsqueda está completa: cada solución adecuada se encontrará después de un tiempo finito. Por ejemplo, en el lenguaje Prolog esto no es así. Hace algo así como un rastreo profundo (que puede colgar en una rama infinita), y la búsqueda entrelazada es esencialmente una modificación difícil de rastreo amplio.

Veamos ahora cómo funciona la primera consulta de la sección anterior. Como appendo tiene llamadas recursivas, agregaremos índices a las variables para distinguirlas. La siguiente figura muestra el árbol de enumeración. Las flechas indican la dirección de difusión de la información (con la excepción del retorno de la recursividad). Entre disyunciones, la información no se distribuye, y entre conjunciones se distribuye de izquierda a derecha.

Comenzamos con una llamada externa para anexar. La rama izquierda de la disyunción muere debido a la controversia: lista $a$ no vacio
En la rama derecha se introducen variables auxiliares, que luego se utilizan para "analizar" la lista $a_1$ en la cabeza y la cola.
Después de esto, la llamada recursiva appendo ocurre para a = [2], b = [3, 4], ab = ?, en la cual ocurren operaciones similares.
Pero en la tercera llamada al apéndice, ya tenemos a = [], b = [3,4], ab =?, Y luego la disyunción izquierda simplemente funciona, después de lo cual obtenemos la información ab = b. Pero en la rama derecha hay una contradicción.
Ahora podemos escribir toda la información disponible y restaurar la respuesta sustituyendo los valores de las variables:

a_1 = [1, 2] b_1 = [3, 4] ab_1 = Cons h_1 tb_1 h_1 = 1 a_2 = t_1 = [2] b_2 = b_1 = [3, 4] ab_2 = tb_1 = Cons h_2 tb_2 h_2 = 2 a_3 = t_2 = Nil b_3 = b_2 = b_1 = [3, 4] ab_3 = tb_2 = b_3 = [3, 4]
Se sigue que $ab_1$ = Contras (1, Contras (2, [3, 4])) = [1, 2, 3, 4], según sea necesario.

Lo que hice en la licenciatura

Todo se ralentiza

Como siempre: le prometen que todo será súper declarativo, pero en realidad necesita adaptarse al lenguaje y escribir todo de una manera especial (teniendo en cuenta cómo se ejecutará todo) para que al menos algo funcione, excepto los ejemplos más simples. Esto es decepcionante.

Uno de los primeros problemas a los que se enfrenta un programador principiante de miniKanren es que depende en gran medida del orden en que describa las condiciones (conjuntos) en el programa. Con una orden, todo está bien, pero se intercambiaron dos conjunciones y todo comenzó a funcionar muy lentamente o no terminó en absoluto. Esto es inesperado

Incluso en el ejemplo con appendo, el lanzamiento en la dirección opuesta (generando la división de la lista en dos) no finaliza a menos que especifique explícitamente cuántas respuestas desea (luego la búsqueda finalizará después de encontrar el número requerido).

Supongamos que arreglamos las variables originales de la siguiente manera: a = ?, B = ?, Ab = [1, 2, 3] (vea la figura a continuación) En la segunda rama, esta información no se utilizará de ninguna manera durante una llamada recursiva (la variable ab y restricciones en

h_{1}

$h_1$ y

t b_{1}

$tb_1$ aparecer solo después de esta llamada). Por lo tanto, en la primera llamada recursiva, todos sus argumentos serán variables libres. Esta llamada generará todo tipo de triples a partir de dos listas y su concatenación (y esta generación nunca terminará), y luego entre ellas se elegirán aquellas para las cuales el tercer elemento es exactamente el que necesitamos.

No todo es tan malo como podría parecer a primera vista, porque clasificaremos estos triples en grupos grandes. Las listas con la misma longitud pero elementos diferentes no difieren desde el punto de vista de la función, por lo tanto, caerán en una solución: habrá variables libres en lugar de los elementos. Sin embargo, seguiremos clasificando todas las longitudes posibles de la lista, aunque solo necesitamos una, y sabemos cuál. Este es un uso muy irracional (no uso) de la información en la búsqueda.

Este ejemplo específico es fácil de solucionar: solo necesita mover la llamada recursiva hasta el final y todo funcionará como debería. Antes de la llamada recursiva, se realizará la unificación con la variable ab y la llamada recursiva se realizará desde la cola de la lista dada (como una función recursiva normal). Esta definición con una llamada recursiva al final funcionará bien en todas las direcciones: a la llamada recursiva, logramos acumular toda la información posible sobre los argumentos.

Sin embargo, en cualquier ejemplo un poco más complejo, cuando hay varias llamadas significativas, no existe un orden específico para el que todo estará bien. El ejemplo más simple: expandir una lista usando concatenación. Arreglamos el primer argumento, necesitamos este orden en particular, arreglamos el segundo, necesitamos intercambiar las llamadas. De lo contrario, se busca durante mucho tiempo y la búsqueda no finaliza.

 reverso x xr = (x === Nil &&& xr == Nil) ||| (fresh (ht tr) (x === Cons (h, t)) (reverso t tr) (appendo tr (Cons (h, Nil)) xr))

Esto se debe a que los procesos de búsqueda intercalados se conjugan secuencialmente y nadie podría pensar en cómo hacerlo de manera diferente sin perder una eficiencia aceptable, aunque lo intentaron. Por supuesto, algún día se encontrarán todas las soluciones, pero con el orden incorrecto, se buscarán durante un tiempo tan poco realista que no tiene sentido práctico.

Existen técnicas para escribir programas para evitar este problema. Pero muchos de ellos requieren habilidades e imaginación especiales para su uso, y el resultado son programas muy grandes. Un ejemplo es el término técnica de límite de tamaño y la definición de división binaria con el resto mediante la multiplicación con su ayuda. En lugar de escribir estúpidamente una definición matemática

 divo nmqr = (fresh (mq) (multo mq mq) (pluso mq rn) (lto rm))

Tengo que escribir una definición recursiva de 20 líneas + una gran función auxiliar que no es realista de leer (todavía no entiendo lo que se está haciendo allí). Se puede encontrar en la disertación de Will Bird en la sección Aritmética binaria pura.

En vista de lo anterior, me gustaría proponer algún tipo de modificación de búsqueda para que los programas simples y naturalmente escritos también funcionen.

Optimizar

Notamos que cuando todo está mal, la búsqueda no terminará a menos que indique explícitamente el número de respuestas y lo rompa. Por lo tanto, decidieron luchar precisamente con lo incompleto de la búsqueda: es mucho más fácil concretar que "funciona durante mucho tiempo". En general, por supuesto, solo quiero acelerar la búsqueda, pero es mucho más difícil de formalizar, así que comenzamos con una tarea menos ambiciosa.

En la mayoría de los casos, cuando la búsqueda diverge, ocurre una situación que es fácil de rastrear. Si una función se llama recursivamente, y en una llamada recursiva, los argumentos son iguales o menos específicos, entonces en la llamada recursiva se genera otra subtarea de este tipo y se produce una recursión infinita. Formalmente, suena así: hay una sustitución, aplicando cuál a los nuevos argumentos, obtenemos los viejos. Por ejemplo, en la figura a continuación, una llamada recursiva es una generalización del original: puede sustituir

c_{2}

$c_2$ = [x, 3]

d_{2}

$d_2$ = x y recibe la llamada original.

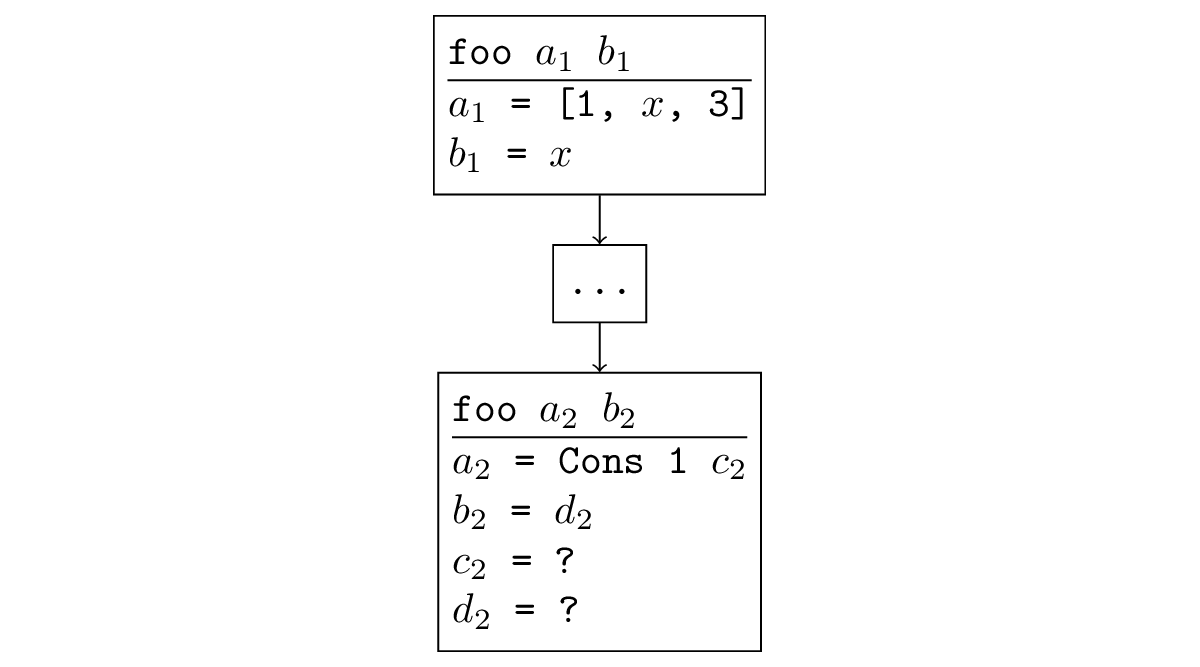
Se puede rastrear que esta situación también ocurre en los ejemplos de divergencia que ya hemos conocido. Como escribí anteriormente, cuando ejecuta appendo en la dirección opuesta, se realizará una llamada recursiva con variables libres en lugar de todas las variables, que, por supuesto, es menos específica que la llamada original, en la que se solucionó el tercer argumento.

Si corremos reverso con x =? y xr = [1, 2, 3], se puede ver que la primera llamada recursiva volverá a suceder con dos variables libres, por lo que, obviamente, los nuevos argumentos pueden transferirse nuevamente a los anteriores.

 reverso x x_r  (* x = ?, x_r = [1, 2, 3] *) fresh (ht t_r) (x === Cons (h, t)) (* x_r = [1, 2, 3] = Cons 1 (Cons 2 (Cons 3 Nil))) x = Cons (h, t) *) (reverso t t_r) (* :   t=x, t_r=[1,2,3],    *)

Usando este criterio, podemos detectar divergencias en el proceso de ejecución del programa, entender que todo está mal con este orden y cambiarlo dinámicamente a otro. Gracias a esto, idealmente, se seleccionará el orden correcto para cada llamada.
Puede hacerlo ingenuamente: si se encuentra divergencia en el conjunto, entonces ingresamos todas las respuestas que ya encontró y posponemos su ejecución para más adelante, "saltando" el próximo conjunto. Entonces, quizás, cuando continuemos ejecutándolo, ya se conocerá más información y no surgirán divergencias. En nuestros ejemplos, esto conducirá a los conjuntos de intercambio deseados.

Hay formas menos ingenuas que permiten, por ejemplo, no perder el trabajo ya realizado, posponiendo el rendimiento. Ya con la variante más estúpida de cambiar el orden, la divergencia ha desaparecido en todos los ejemplos simples que sufren de la no conmutatividad de la conjunción, que sabemos, incluyendo:

ordenar la lista de números (también es la generación de todas las permutaciones de la lista),
Aritmética de peano y aritmética binaria,
generación de árboles binarios de un tamaño dado.

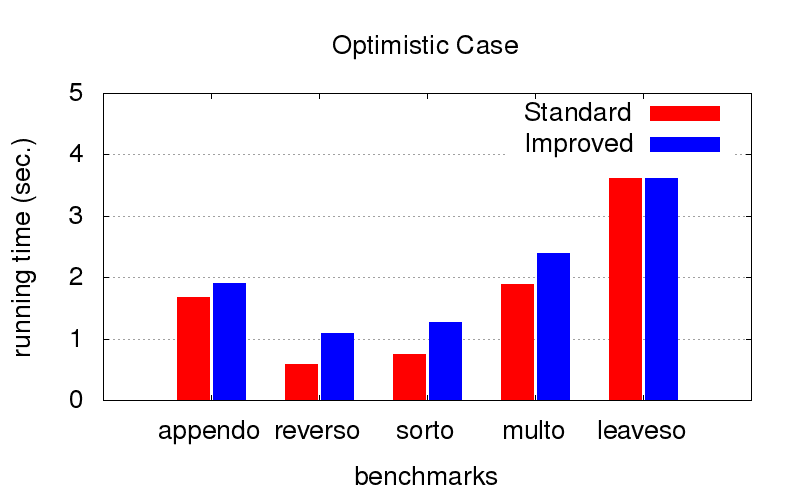
Esta fue una sorpresa inesperada para nosotros. Además de la divergencia, la optimización también lucha contra la desaceleración del programa. Los diagramas a continuación muestran el tiempo de ejecución de programas con dos órdenes diferentes en conjunciones (relativamente hablando, uno de los mejores y uno de muchos malos). Fue lanzado en una computadora con la configuración de Intel Core i7 CPU M 620, 2.67GHz x 4, 8GB de RAM con el sistema operativo Ubuntu 16.04.

Cuando el orden ya es óptimo (lo seleccionamos a mano), la optimización ralentiza un poco la ejecución, pero no es crítica

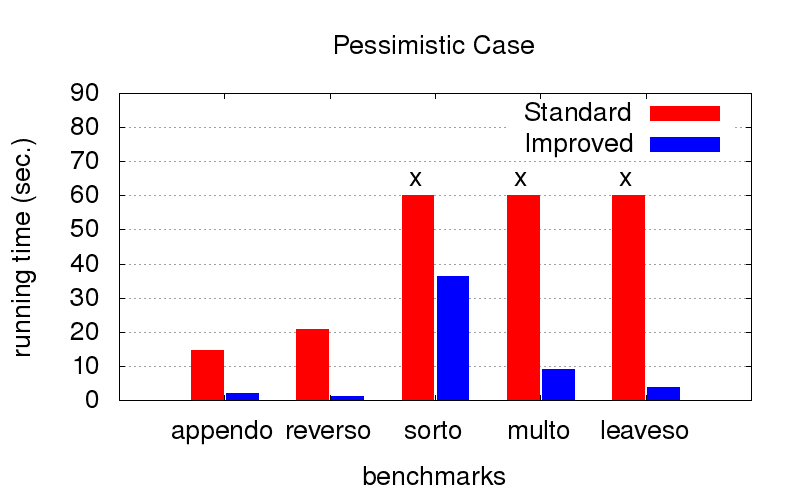
Pero cuando el orden no es óptimo (por ejemplo, adecuado solo para lanzar en la dirección opuesta), con la optimización resulta mucho más rápido. Las cruces significan que simplemente no podíamos esperar hasta el final, funciona mucho más tiempo

Como no romper nada

Todo esto se basó exclusivamente en la intuición y queríamos demostrarlo estrictamente. Teoría después de todo.

Para probar algo, necesitamos una semántica formal del lenguaje. Describimos la semántica operativa para miniKanren. Esta es una versión simplificada y matematizada de una implementación de lenguaje real. Utiliza una versión muy limitada (por lo tanto, fácil de usar), en la que puede especificar solo la ejecución final de los programas (la búsqueda debe ser final). Pero para nuestros propósitos, esto es exactamente lo que se necesita.

Para probar el criterio, primero se formula el lema: la ejecución del programa desde un estado más general funcionará por más tiempo. Formalmente: el árbol de salida en semántica tiene una gran altura. Esto se prueba por inducción, pero la afirmación debe generalizarse con mucho cuidado, de lo contrario la hipótesis inductiva no será lo suficientemente fuerte. De este lema se desprende que si un criterio funcionó durante la ejecución del programa, entonces el árbol de salida tiene su propio subárbol de mayor o igual altura. Esto da una contradicción, ya que para la semántica dada inductivamente todos los árboles son finitos. Esto significa que en nuestra semántica la ejecución de este programa es inexpresable, lo que implica que la búsqueda en él no termina.

El método propuesto es conservador: cambiamos algo solo cuando estamos convencidos de que todo ya es completamente malo e imposible de empeorar, por lo tanto, no rompemos nada en términos de finalización del programa.

La prueba principal contiene muchos detalles, por lo que teníamos el deseo de verificarlo formalmente escribiendo a Coq . Sin embargo, resultó ser bastante difícil técnicamente, por lo que enfriamos nuestro ardor y nos dedicamos seriamente a la verificación automática solo en la magistratura.

Publicar

En el medio del trabajo, presentamos este estudio en la sesión de pósters de ICFP-2017 en la Competencia de Investigación Estudiantil . Allí nos reunimos con los creadores del lenguaje, Will Bird y Daniel Friedman, y dijeron que es significativo y que debemos analizarlo con más detalle. Por cierto, Will es generalmente amigo de nuestro laboratorio en JetBrains Research. Toda nuestra investigación sobre miniKanren comenzó cuando, en 2015, Will realizó una escuela de verano en programación relacional en San Petersburgo.

Un año después, llevamos nuestro trabajo a una forma más o menos completa y presentamos el artículo en Principios y práctica de la programación declarativa 2018.

¿Qué hago en la escuela de posgrado?

Queríamos continuar participando en la semántica formal para miniKanren y una prueba rigurosa de todas sus propiedades. En la literatura, generalmente las propiedades (a menudo lejos de ser obvias) simplemente se postulan y demuestran mediante ejemplos, pero nadie prueba nada. Por ejemplo, el libro principal sobre programación relacional es una lista de preguntas y respuestas, cada una de las cuales está dedicada a un código específico. Incluso para la declaración de integridad de la búsqueda entrelazada (y esta es una de las ventajas más importantes de miniKanren sobre Prolog estándar), es imposible encontrar una redacción estricta. Decidimos que no puedes vivir así y, después de recibir una bendición de Will, nos pusimos a trabajar.

Permítame recordarle que la semántica que desarrollamos en la etapa anterior tenía una limitación significativa: solo se describieron los programas con búsqueda finita. En miniKanren, los programas en ejecución también son interesantes porque pueden enumerar un número infinito de respuestas. Por lo tanto, necesitábamos una semántica más genial.

Hay muchas formas estándar diferentes para definir la semántica de un lenguaje de programación, solo tuvimos que elegir una de ellas y adaptarla a un caso específico. Describimos la semántica como un sistema de transición etiquetado: un conjunto de posibles estados en el proceso de búsqueda y transiciones entre estos estados, algunos de los cuales están marcados, lo que significa que en la etapa actual de la búsqueda, se encontró otra respuesta. La ejecución de un programa en particular está determinada por la secuencia de tales transiciones. Estas secuencias pueden ser finitas (llegando a un estado terminal) o infinitas, describiendo simultáneamente la finalización y la no finalización de programas. Para especificar completamente dicho objeto matemáticamente, uno necesita usar una definición coinductiva.

— . , (, , — ..). , miniKanren' ( ).

, , — . . ( ), , .
( ): , , , .

, , / .

Coq'a. , , «. Qed». .

Programación relacional: dolor, interés y dolor de nuevo.