✌️ 👩🏿‍🤝‍👨🏾 🤴🏿 Wolfensteiny 3D - ingeniería inversa 251 bytes de JavaScript 👨🏽‍🔬 👎🏾 🐾

Al escribir código, muchos no piensan en otra cosa que no sea la lógica del programa en sí. Menos personas piensan en optimizar el código con el tiempo, desde la memoria. Pero solo unos pocos alcanzan el último nivel: comprimir el programa a un tamaño récord.

Mire, por ejemplo, el resultado de solo 251 bytes de JavaScript:

Bueno, ¡descubramos cómo funciona!

De donde es

Este código, así como gran parte de lo que recurrí en este artículo, se encuentra en el sitio p01.org del magnífico Mathieu 'p01' Henri, un desarrollador de JavaScript y no solo a menudo involucrado en comprimir el código a tamaños imposibles. El material fuente de este artículo está aquí .

Entonces, antes de que estén los 251 bytes del código fuente.

<body onload=E=c.getContext("2d"),setInterval(F="t+=.2,Q=Math.cos;c.height=300;for(x=h;x--;)for(y=h;y--;E.fillRect(x*4,y*4,bd?4:D/2,D/2))for(D=0;'.'<F[D*y/hD/2|0?1:(d=t+D*Q(T=x/h-.5+Q(t)/8)&7)|(3.5+D*Q(T-8))<<3]&&D<8;b=d)D+=.1",t=h=75)><canvas id=c>

Está claro que nada está claro.

Hacer el código legible

En primer lugar, pongo todo el código JavaScript en una etiqueta separada, por conveniencia.

Se puede ver que las variables E , h , Q , F y otras son constantes que se pueden reemplazar con sus propios valores / objetos, así como cambiar los nombres.

 var context = c.getContext("2d") var F="t+=.2,Q=Math.cos;c.height=300;for(x=h;x--;)for(y=h;y--;E.fillRect(x*4,y*4,bd?4:D/2,D/2))for(D=0;'.'<F[D*y/hD/2|0?1:(d=t+D*Q(T=x/h-.5+Q(t)/8)&7)|(3.5+D*Q(T-8))<<3]&&D<8;b=d)D+=.1" var t = 75 var size = 75 function render(){ t += 0.2; c.height=300; for(let x = size; x--;) for(let y = size; y--; context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2)) for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1 } setInterval(render, 75);

Aquí, el código de la cadena ya se ha extraído de la función, y la cadena en sí está intacta, lo necesitaremos en el futuro.

Ahora convierta los dos bucles externos a while .

 function render(){ t += 0.2; c.height=300; let x = size; while(x > 0){ let y = size; while(y > 0){ for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1 context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2); y--; } x--; } }

¿Cómo vemos esto?

Vamos a entender por qué lo vemos en absoluto. Si miras la imagen de nuevo, puedes entender mucho.

Imagen en la que se puede hacer clic

Aquí está lo que vemos:

Cuanto más lejos está el sujeto, más oscuro es
La parte oblicua de los obstáculos encontrados se inunda de manera diferente con líneas, no puntos.

En el código, el dibujo se refleja así:

 // ,  ,       //   ||     // | | || | | // ↓ ↓ ↓↓ ↓ ↓ context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2);

¿Por qué vemos objetos volumétricos en esta inundación de puntos negros? Después de todo, tenemos que contentarnos solo con diferentes tonos de negro: el tamaño de los puntos negros (no podemos cambiar el color, ¡ E.fillStyle es demasiado largo!). De hecho, funciona simplemente porque en una imagen bidimensional, nuestro ojo se basa principalmente en la sombra y el brillo de la luz.

Imagínese caminando por un corredor oscuro con solo una linterna en sus manos. Brillas frente a ti y ves que algunos objetos están más cerca y más brillantes (una linterna brilla, un obstáculo es brillante, no hay sombras), mientras que otros están más lejos y más oscuros (la luz está dispersa, débil y vemos oscuridad, y sentimos la distancia). Entonces, aquí: cuanto más lejos esté el objeto ( D más grande), mayor será el tamaño que dibujemos un cuadrado negro en la pantalla.
Pero, ¿cómo sabemos qué debe ser brillante y qué no?

Cuenta el píxel

Ahora tratemos con este monstruo:

 for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1

Entonces Toda esta expresión es un algoritmo de marcación por rayos de paso fijo que le permite encontrar la intersección de la viga con los bloques. Para cada píxel de la pantalla, lanzamos un rayo, y lo seguimos con un paso fijo de 0.1 , y tan pronto como encontramos un obstáculo, terminamos el algoritmo y dibujamos un píxel en la pantalla, sabiendo la distancia al obstáculo.

Comencemos a leer este código en partes.

Condición D * y / size - D / 2 | 0 D * y / size - D / 2 | 0 puede representarse como

D * (f r a c y s i z e - f r a c 12) = D * (f r a c y - s i z e / 2 s i z e) < 1

$D * (\ frac {y} {size} - \ frac {1} {2}) = D * (\ frac {y - size / 2} {size}) <1$ , la expresión entre paréntesis mostrará la "desviación" y del centro de la pantalla (en fracciones de la pantalla). Así que estamos tratando de entender si la viga está entre el piso y el techo o no. Por lo tanto, si tocamos el piso (o el techo), salimos más del bucle, para dibujar y dibujar un píxel.
Y si no tocamos, entonces continuamos los cálculos: buscamos las coordenadas actuales del haz.

 var T = x / size - .5 + Math.cos(t) / 8; // Math.cos(t)   //    var xcoord = t + depth * Math.cos(T); var ycoord = 3.5 + depth * Math.cos(T - 8); //

¿Por qué cos (T - 8)?

Entonces resulta que

c o s (x - 8) a p r o x s i n (x)

$cos (x-8) \ aprox sin (x)$ con una precisión de 0,15 radianes. Todo porque

f r a c 5 p i 2 a p r o x 8.15 a p r o x 8

$\ frac {5 \ pi} {2} \ aprox 8.15 \ aprox 8$

y luego

c o s (a l p h a - 8) a p r o x c o s (a l p h a - f r a c 5 p i 2) = c o s (a l p h a - f r a c p i 2) = s i n (a l p h a)

$cos (\ alpha-8) \ aprox cos (\ alpha- \ frac {5 \ pi} {2}) = cos (\ alpha - \ frac {\ pi} {2}) = sin (\ alpha)$

Vale la pena hablar sobre cómo se verifica un punto en el espacio para un bloque en general. La tarjeta en sí se toma del código fuente ( F ) y tiene este aspecto:

 t+=.2,Q= ----> ░█░█░█░░ Math.cos ----> ░░░░█░░░ ;c.heigh ----> ░░█░░░░░   - t=300;fo ----> ░░░░░░░░ <----  , r(x=h;x- ----> ░█░░░░░█     -;)for(y ----> █░█░░░█░ =h;y--;E ----> ░░░░██░░ .fillRec ----> █░░░░░░░

Parece que está en movimiento, el campo de visión de la cámara se indica aquí.

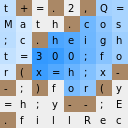
Las celdas cuyo código de símbolo es menor que el código de punto - "." Están marcadas en oscuro "." - es decir, los caracteres !"#$%&'()*+,-. Ahora redondeamos las coordenadas de la viga e intentamos averiguar si la letra en el índice de" coordenadas "dado es oscura (obstáculo) o no (vuela la viga más lejos).

Como el índice es uno y las coordenadas son dos, entonces usamos el hack:

 var boxIndex = xcoord & 7 | ycoord << 3;

Como resultado, obtenemos un número que refleja el número de bloque (bueno o nulos).

Volvamos al código. Ahora se ve decente.

El código es un poco gordo

 function render(){ t += 0.2; c.height=300; let x = size; while(x > 0){ let y = size; while(y > 0){ var depth = 0 while(depth < 8){ depth += 0.1 var T = x / size - .5 + Math.cos(t) / 8; //   var isFloorOrCeiling = depth * y / size - depth / 2 | 0; //      ? if(isFloorOrCeiling) break; var xcoord = t + depth * Math.cos(T) & 7; var ycoord = 3.5 + depth * Math.sin(T); // cos - 8 -> sin boxIndex = xcoord | ycoord << 3; //     , //    if ('.' >= F[boxIndex]) break; b = xcoord; //  ?  ! } context.fillRect(x * 4, y * 4, b - xcoord ? 4 : depth / 2, depth / 2) y--; } x--; } }

Volver al dibujo

¿Por qué necesitamos todo esto? Ahora, después de ejecutar este algoritmo, sabemos la distancia al objeto y podemos dibujarlo. Pero una pregunta quedó sin respuesta: ¿cómo distinguir el techo de una unidad separada? Después de todo, ¡la distancia al techo y al bloque son números que no son diferentes! De hecho, ya hemos respondido esta pregunta.

 // ,  ,      // || // ↓↓ context.fillRect(x * 4, y * 4, b - xcoord ? 4 : depth / 2, depth / 2);

Hay una condición en el código relacionada con la variable b , y que afecta el ancho del "píxel negro grande": b - xcoord ? 4 : depth / 2 b - xcoord ? 4 : depth / 2 . Eliminemos esta condición y veamos qué sucede sin ella:

¡No hay fronteras entre los bloques y el techo! (se puede hacer clic)

Condición b - xcoord nos dará un ancho constante cuando el cambio de coordenadas sea 0. ¿Y cuándo no puede suceder esto? Esto no sucede solo cuando no llegamos a la línea (2) en el código:

 // .... var xcoord = t + depth * Math.cos(T) & 7; // <---    (1) // ... if ('.' >= F[boxIndex]) // <---    (3) break; b = xcoord; // <---     (2) // ....

Esto significa que el programa sale del ciclo antes, en la línea (3) , cuando el rayo entra en un bloque opaco en la dirección casi perpendicular a su pared, es decir, cae en la cara "cara" del bloque. Por lo tanto, todos los bloques son diferentes del piso y el techo.

Entonces, así es como resulta esta hermosa imagen en 3D, que no solo agrada a la vista, sino que también te hace pensar cómo y por qué funciona. Puede ver este código en acción aquí (fuera. Sitio del desarrollador de este milagro).

Wolfensteiny 3D - ingeniería inversa 251 bytes de JavaScript

Hacer el código legible

¿Cómo vemos esto?

Cuenta el píxel

Volver al dibujo

More articles: