En 1974, el matemático británico Roger Penrose creó un conjunto revolucionario de mosaicos que se pueden usar para llenar un plano infinito con un patrón que nunca se repite. En 1982, el cristalógrafo israelí Daniel Shekhtman descubrió una aleación de metal cuyos átomos estaban dispuestos en un orden nunca antes encontrado en la ciencia de los materiales. Penrose logró un reconocimiento público masivo, rara vez otorgado a los matemáticos. Shekhtman recibió el Premio Nobel. Ambos científicos desafiaron la intuición humana y cambiaron los conceptos básicos para comprender la estructura de la naturaleza, descubriendo que la variabilidad infinita puede ocurrir incluso en un entorno altamente ordenado.
En el centro de sus descubrimientos se encuentra una "simetría prohibida", llamada así porque contradice la conexión profundamente arraigada entre simetría y repetibilidad. La simetría se basa en los ejes de reflexión: todo lo que está en un lado de la línea está duplicado en el otro. En matemáticas, esta conexión se expresa mediante patrones de espacio en mosaico. Las formas simétricas, como rectángulos y triángulos, pueden llenar el plano sin espacios ni superposiciones, creando un patrón que se repite constantemente. Los patrones repetidos se denominan "periódicos" y se dice que tienen "simetría de transferencia". Si mueve el patrón (patrón) de un lugar a otro, se verá igual.
Como científico audaz y ambicioso, Penrose estaba más interesado no en los mismos patrones y repetibilidad, sino en la variabilidad infinita. Más específicamente, estaba interesado en el mosaico “aperiódico”, es decir, conjuntos de figuras que pueden llenar un plano infinito sin espacios y superposiciones, y el patrón de mosaico nunca se repite. Esta fue una tarea difícil porque no podía usar figuras (mosaicos) con dos, tres, cuatro o seis ejes de simetría: rectángulos, triángulos, cuadrados o hexágonos, porque en un plano infinito crearían patrones periódicos o repetitivos. Es decir, necesitaba usar figuras que se pensaba que dejaban huecos al llenar el avión, figuras que han prohibido la simetría.
Para crear su propio plano de patrones no repetitivos, Penrose recurrió a la simetría de cinco ejes, a los pentágonos, en particular porque, según él, es "simplemente agradable mirar pentágonos". Lo notable de las figuras de Penrose fue que, aunque las obtuvo de las líneas y las esquinas de los rectángulos, no dejaron huecos feos. Se ajustan entre sí, se doblan y giran en el avión, siempre están cerca de la repetibilidad, pero nunca lo alcanzan.
El mosaico de Penrose ha captado la atención del público por dos razones principales. Primero, encontró una manera de generar patrones infinitamente cambiantes a partir de solo dos tipos de formas. En segundo lugar, sus azulejos eran figuras simples y simétricas, que en sí mismas no mostraban signos de propiedades inusuales.

Penrose creó varias variedades de sus juegos aperiódicos de figuras. Uno de los más famosos se llama "serpiente" y "dardo". La "cometa" se parece a la cometa de un niño, y el "dardo" se parece a un esquema simplificado de un bombardero sigiloso. Ambos están claramente divididos a lo largo de los ejes de simetría y cada uno de ellos tiene arcos simétricos simples en la superficie. Penrose definió una regla para colocar formas: para la colocación "adecuada" de los mosaicos, estos arcos deben coincidir, creando curvas inextricables. Sin esta regla, las "serpientes" y los "dardos" se pueden organizar en patrones repetitivos. Si sigue esta regla, entonces la repetición nunca ocurre. "Serpiente" y "dardo" llenan infinitamente el avión, bailando alrededor de sus cinco ejes, creando estrellas y decágonos, curvas curvas, mariposas y flores. Las figuras se repiten, pero aparecen nuevas variaciones en ellas.
El profesor clínico de matemáticas Edmund Harriss, de la Universidad de Arkansas, que escribió un doctorado sobre azulejos de Penrose, ofrece tal comparación. “Imagina que vives en un mundo de cuadrados. Empiezas a caminar, y cuando llegas al final de la plaza, la siguiente es exactamente la misma, y sabes lo que verás si continúas moviéndote sin parar ". Las baldosas de Penrose tienen exactamente la naturaleza opuesta. “Cualquiera sea la información que tenga, cualquiera que sea la parte del patrón que vea, nunca podrá predecir lo que sucederá después. Siempre habrá algo que no has visto antes ".
Uno de los aspectos curiosos de la división aperiódica de un avión es que la información de posicionamiento se transmite de alguna manera a largas distancias: el mosaico de Penrose, colocado en un lugar, interfiere con la colocación de otros mosaicos en los cientos (y también miles y millones) de mosaicos. "Una restricción local de alguna manera crea una restricción global", dice Harriss. "Esto sugiere que en ninguna escala estos mosaicos crearán algo periódico". Es posible que tenga la opción de colocar, por ejemplo, una "serpiente" en un área, o un "dardo" en algún lugar remoto. Cualquiera de las fichas funcionará, pero no ambas.
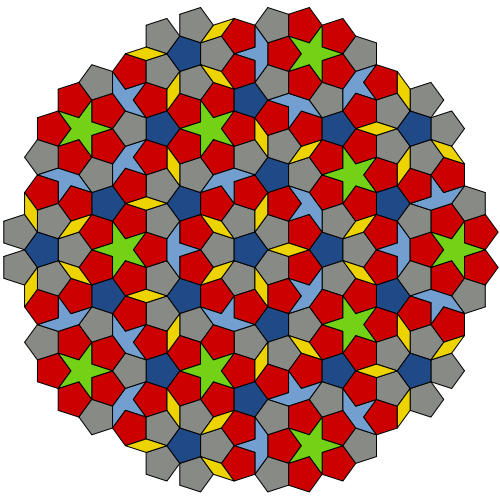
Estas fichas, que forman un patrón interminable y no repetitivo, expresan la relación de Fibonacci, también conocida como la "proporción áurea". Se dice que dos números tienen una proporción áurea si la razón de un número más pequeño a uno más grande es la misma que la razón de un número más grande a la suma de dos números. En este caso, la proporción del área de la "serpiente" al área del "dardo" es la proporción áurea. La relación entre el lado largo de la "serpiente" y su lado corto es también la relación dorada.
Los mosaicos de Penrose también se pueden subdividir en versiones más pequeñas de ellos mismos. Una "serpiente" consiste en dos "serpientes" más pequeñas y dos mitades de un "dardo". El "dardo" consiste en una "serpiente" más pequeña y dos alfombras "dardo". (En cualquier mosaico apropiado de Penrose, estas mitades de los "dardos" están alineadas entre sí. Desde el punto de vista de las matemáticas, esto les permite ser considerados como "dardos" completos). "" Dice Harriss. "Si los subdivido, obtendré 2" serpientes "
A +
B y " dardos "
A +
B.Si realiza esta sustitución un número infinito de veces, puede calcular la participación total de cada tipo de mosaico, como si se dispusiera en un plano infinito. En tales cálculos, un patrón
repetitivo siempre conduce a un número racional. Si la proporción es un número irracional, esto significa que el patrón nunca se repetirá por completo. En los cálculos para las fichas de Penrose, no solo se obtiene el número irracional, sino que su proporción es la proporción de Fibonacci, la proporción de "dardos" a "serpientes" es igual a la proporción de "serpientes" al número total de fichas.
Dado que la proporción de Fibonacci es de naturaleza ubicua, desde las piñas hasta las poblaciones de conejos, es aún más extraño que esta proporción sea fundamental para el sistema de mosaico, que, al parecer, no tiene nada que ver con el mundo físico. Penrose creó algo nuevo en la ciencia, intrigando precisamente allí que no debería funcionar como lo hace la naturaleza. Fue como si Penrose escribiera una historia de ciencia ficción sobre una nueva especie de animal, y luego el zoólogo descubrió esta especie que vivía en la Tierra. De hecho, las fichas de Penrose están asociadas con la proporción áurea, con las matemáticas que inventamos y las matemáticas del mundo que nos rodea.

Al comenzar el estudio de la simetría prohibida, Penrose no podría haber adivinado que se había convertido en parte del cambio de pensamiento que condujo al descubrimiento de un nuevo campo de la ciencia matemática. Después de todo, la simetría es fundamental tanto para las matemáticas puras como para el mundo natural. El astrofísico Mario Livio llamó a la simetría "una de las herramientas más necesarias para descifrar la estructura de la naturaleza". La naturaleza usa cuadrados y hexágonos por la misma razón que los humanos: son simples, eficientes y ordenados. Si los pentágonos parecían poco prácticos incluso para una tarea tan simple como llenar baldosas en el diseño de interiores, entonces, por supuesto, se creía que no podían usarse para crear átomos en materiales sólidos como los cristales.
Los cristales consisten en redes tridimensionales de átomos. Los cristales crecen agregando nuevos átomos y expandiendo las redes. Esto sucede más eficientemente cuando los átomos se alinean en patrones repetitivos. Durante décadas, la historia terminó allí: los cristales eran estructuras repetitivas. El punto
Pero luego, en 1982, Shekhtman se fue de licencia creativa de la Universidad de Technion en Haifa y comenzó a trabajar en la Oficina Nacional de Normas. Buscó en un laboratorio de aleación de aluminio y manganeso. Los patrones de difracción creados por sus estructuras cristalinas no parecen parecerse a ninguna de las simetrías estándar conocidas por los cristalógrafos. De hecho, los átomos se alinearon en los mismos pentágonos, rombos, "serpientes" y "dardos" que Penrose descubrió en el mundo de las matemáticas.
"Por supuesto, estaba familiarizado con las baldosas de Penrose", dice Schechtman. Pero no tenía ninguna razón para sospechar su conexión con esta aleación. “No entendí lo que es. Durante los siguientes meses, repetí mis experimentos una y otra vez. Al final de mis vacaciones creativas, sabía exactamente lo que no era, pero aún no tenía idea de lo que era ".
Para comprender lo que descubrió, Schechtman, como Penrose, tuvo que cuestionar sus ideas intuitivas habituales. Tenía que aceptar la simetría prohibida y su confusión pentagonal con una falta de repetibilidad. Mientras estuvo en Israel, se mostró reacio a reconocer que había descubierto una estructura atómica cristalina no repetitiva. Sin embargo, nadie en el mundo de la ciencia de los materiales al principio podría atribuir este descubrimiento a los cristales. Por lo tanto, fueron llamados "cuasicristales".
Las extrañas matemáticas de Penrose parecían haberse introducido en el mundo natural. "Durante 80 años, los cristales se han definido como estructuras" ordenadas y periódicas ", porque todos los cristales que estudiamos desde 1912 eran periódicos", explica Schechtman. “No fue hasta 1992 que la Unión Internacional de Cristalografistas organizó un comité para seleccionar una nueva definición para la palabra cristal. Esta nueva definición es un cambio de paradigma para la cristalografía ".
No fue solo la simple inercia del pensamiento lo que impidió que Shekhtman entendiera y aceptara el descubrimiento. Las estructuras cristalinas aperiódicas no solo no eran familiares, sino que se consideraban antinaturales. Recuerde que la ubicación de un mosaico de Penrose puede afectar las formas en los miles de mosaicos que contiene: las restricciones locales crean las globales. Pero si un cristal se forma átomo por átomo, entonces no debería haber una ley de la naturaleza que cree las restricciones inherentes a las baldosas de Penrose.
Resultó que los cristales no siempre forman átomo por átomo. “En compuestos intermetálicos muy complejos, los elementos son enormes. No son locales ”, dice Schechtman. Cuando se forman grandes fragmentos de cristal al mismo tiempo, en lugar de por el crecimiento gradual de los átomos, los átomos ubicados muy lejos el uno del otro pueden influir en la posición mutua, al igual que en las baldosas de Penrose.
Como es el caso con muchos tabúes, la simetría prohibida ha sido reconocida como una de las formas aceptables de existencia en la naturaleza. Los cuasicristales no solo se convirtieron en objeto de estudio en un nuevo campo de investigación científica: resultó que tienen muchas propiedades útiles que surgen debido a su estructura inusual. Por ejemplo, su configuración asimétrica de átomos les proporciona poca energía superficial, es decir, poco se les puede pegar. Por lo tanto, los recubrimientos cuasicristalinos comenzaron a usarse en utensilios de cocina antiadherentes. (Cuando Penrose creó sus nuevos azulejos, no podía imaginar que se usarían en cristalografía, sin mencionar la fritura de huevos). Además, los cuasicristales generalmente tienen poca fricción y desgaste, por lo que son recubrimientos ideales para rasuradoras y productos quirúrgicos. instrumentos, o cualquier otro instrumento afilado relacionado con el cuerpo humano.

Como las estructuras cuasicristal nunca se repiten, crean patrones de difracción únicos de radiación electromagnética. Los investigadores de fotónica están interesados en cómo afectan la transmisión de luz, la reflectividad y la fotoluminiscencia. Si se enfrían, su resistencia eléctrica cae a un nivel casi cero. Pero también absorben la radiación infrarroja, por lo que se calientan muy rápidamente a altas temperaturas. Debido a esto, resultan ser una adición muy útil a las impresoras 3D, en las que se utiliza polvo de plástico como material de partida. Shekhtman explica: si un polvo cuasiperiódico se mezcla con él y se expone a la radiación infrarroja, entonces el polvo cuasiperiódico "se calienta extremadamente rápido y derrite las partículas de plástico circundantes, lo que los hace pegarse".
Nadie sabe cómo termina la historia de la simetría prohibida. Los matemáticos continúan explorando las propiedades de los mosaicos de Penrose. Los cuasicristales siguen siendo objeto de estudio tanto en investigación fundamental como aplicada. Pero hasta ahora este viaje ha sido increíble. En los últimos 40 años, la simetría de cinco ejes ha pasado de ser poco práctica a valiosa, de antinatural a completamente natural, de prohibida a dominante. Y por esta transformación, debemos agradecer a dos científicos que abandonaron sus ideas habituales para descubrir una nueva forma notable de variaciones infinitas en la naturaleza.
Sobre el autor: Patchen Bars es un periodista y autor con sede en Toronto. Actualmente está trabajando en un libro sobre la relación entre las matemáticas puras y el mundo natural.