Este artículo es una continuación de mi primer artículo
, Fractals in Prime Numbers .
Artículo siguiente:
Fractales en números irracionales. Parte 2
En un artículo anterior, aprendimos cómo dibujar patrones auto-similares usando números primos mutuos. En este artículo mostraré la naturaleza fractal del número
sqrt2 .
Sin prólogo. Debajo del gato.
Definiremos terminología y notación. En matemáticas, los sistemas que se describen a continuación se denominan
billares . Además usaremos este término. Las dimensiones de los billares rectangulares se denotarán por
M (ancho) y
N (altura)
Billar binario
En el artículo anterior, tomamos un billar rectangular con lados
M y
N , lanzó una pelota hacia él y marcó la trayectoria con una línea discontinua a través de la celda:
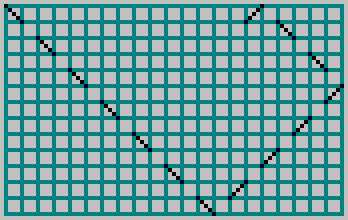
Para mutuamente simple
M y
N obtenemos el patrón:

En la versión binaria, marcamos la trayectoria no con una línea discontinua, sino pintando alternativamente las celdas con blanco y negro (formamos una matriz binaria, ponemos 0 para negro y 1 para blanco en la celda correspondiente):

Reglas de reflexión de borde:
Para mutuamente simple
M y
N la trayectoria pasa por cada celda:

Para diferentes M y NLo más sorprendente de estos patrones es que para diferentes
M y
N Resulta su propio patrón único:





En el artículo, como
M y
N , usamos principalmente números de Fibonacci.
Aquí puede dibujar patrones para otros números (coordenadas del mouse).
Si las partes tienen un divisor común, entonces la pelota entra en la esquina antes de pasar por cada celda:

Es conveniente considerar este caso como billar en un rectángulo con lados
fracMGCD y
fracNGCD (MCD es el factor común más grande):

Antes de continuar, complete la tabla propuesta por el usuario
Captain1312 en su
artículo (dividiremos los lados del billar en GCD).
(1,0) un poco
Para cada mesa de billar
M y
N toma un poco con las coordenadas
(1,0) .
Si
M es un divisor
N - luego un poco con coordenadas
(1,0) faltante (
fracMGCD=1 ) En este caso, tomamos el bit invertido con las coordenadas
(0,1) .
Completa la tabla. El origen es la esquina superior izquierda. Por
x - ancho de billar
M por
y - altura
N . Por cada billar marcamos un poco
(1,0) o bit invertido
(0,1) (volveremos a este tema a continuación).

Un poco sobre los números de FibonacciLa tabla muestra las líneas que emergen de la esquina superior izquierda. Si construyes una tabla así por un momento con coordenadas
(3,0) - Estas líneas se pueden ver aún mejor:

Hay otra forma original de obtener estas líneas.
Para cada
x y
y si
y es un divisor
x , construya una secuencia de números de Fibonacci:
F0=y;F1=x;Fn=Fn−1+Fn−2
Y marque los puntos en el gráfico
(Fn,Fn−1) y
(Fn−1,Fn) :

Secuencia binaria
¿Por qué invertimos la broca cuando el ancho del billar
M=1 ? Para mutuamente simple
M y
N , la trayectoria de la pelota pasa a través de cada celda. Entre las paredes superior e izquierda del billar, la pelota pasa cada vez un número par de celdas.


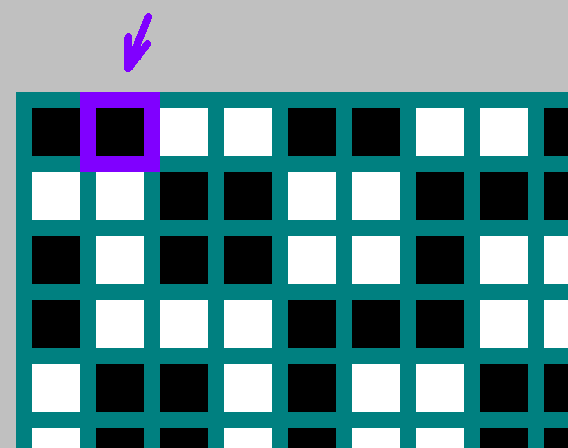
Los bits en la columna izquierda son los bits invertidos de la fila superior. No tomamos el bit cero, la trayectoria comienza con él:
Además, podemos lanzar con seguridad cada segundo bit de esta secuencia (bit
2n−1 - bit invertido
2n ):

Tengo la secuencia
10100110110 para billar
(21,13) . La secuencia es única para todos.
M y
N .
Cualquier altura
N no lo tomamos, la pelota siempre sigue la trayectoria
2N entre dos reflexiones desde la pared superior. Desde la pared superior, el movimiento siempre comienza con un bit "0" (celda negra) y termina con un bit "1" (celda blanca):
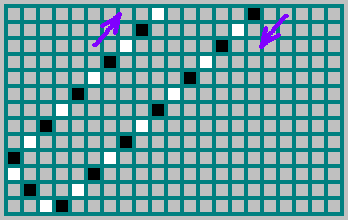
De hecho, la secuencia (que destacamos arriba -
10100110110 ) muestra en qué lado voló la pelota: 1 - si la pelota voló hacia adentro, reflejada desde la pared derecha y 0 - si la pelota voló hacia adentro, reflejada desde la pared izquierda. En la imagen, la trayectoria de la pelota está marcada en negro si la pelota se movió hacia la derecha y blanca si se movió hacia la izquierda:

Es interesanteCon la ayuda de billar, puede dividir dos números en el sistema binario. En el momento de tocar la pared superior o inferior, fijamos la dirección del movimiento de la pelota. Si la pelota se movió a la derecha, escribimos 0. Si a la izquierda, escribimos 1. Arreglaremos cada
2n tocando la pelota
Primer toque de la pared inferior. La pelota se movió hacia la derecha. Fijo 0
El segundo toque es la pared superior. La pelota se movió hacia la izquierda. Fijo 1
El cuarto toque es la pared superior. La pelota se movió hacia la derecha. Fijo 0
El octavo toque está en la pared superior. La pelota se movió hacia la derecha. Fijo 0
Etc.
Obtenido: 0.1001111001111001111 ... es una notación binaria para la fracción
frac1321 .

Esta secuencia (
10100110110 ) contiene toda la información necesaria sobre el patrón. Con él, podemos restaurar el patrón original (e incluso mirar más allá del borde inferior del patrón). Toma un cuadrado con lados
M . Organizamos los bits de nuestra secuencia en aquellos lugares donde la pelota golpea la pared superior (la distancia entre los toques adyacentes de la pelota es de 2 celdas).

Si el bit correspondiente = 1 - comenzamos a movernos hacia la izquierda, marcando la trayectoria a través de la celda. Si bit = 0 - muévase a la derecha.
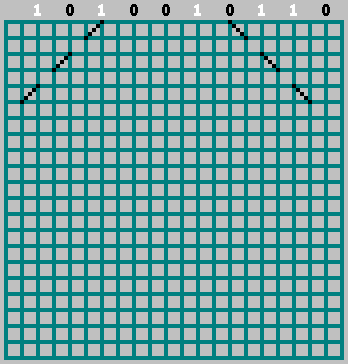
En este caso, no te olvides del bit cero:
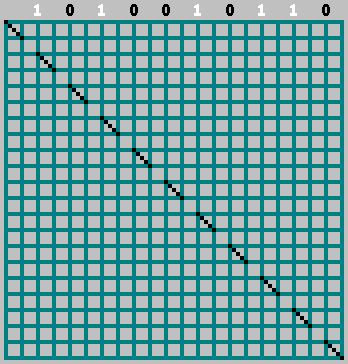
GIF:
Obtuvimos el patrón original (y miramos un poco más allá del borde inferior):
 Script
Script para visualizar secuencias binarias
Podemos construir esta secuencia usando el resto de la división.
Billar unidimensional
En el eje numérico
X toma dos puntos:
0 y
M .

Moviéndose de un punto a otro, mida la distancia
N :
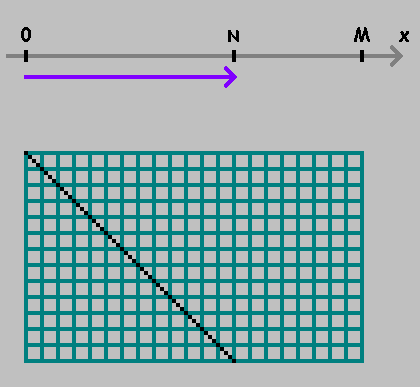
Marcó el punto. Continuamos midiendo la distancia desde este punto, manteniendo la dirección. Si has llegado al punto
0 o
M - cambio de dirección:
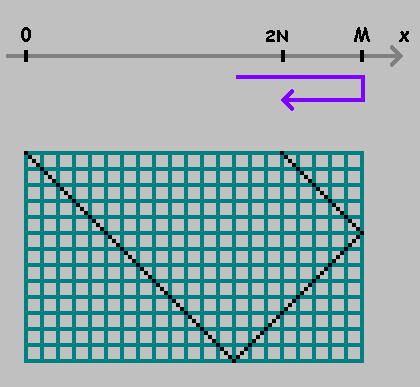
Como se puede ver en las figuras anteriores, el primer punto muestra el lugar donde la pelota toca la pared inferior del billar. Este punto no nos interesa. Solo arreglaremos puntos
2kN para
k=0,1,2,... .
¿Cómo marcar estos puntos? Convierte nuestros billares en el eje
X . Marca los puntos
0,M,2M,3M,... . Ahora llegando al punto
M no cambiamos de dirección, sino que seguimos avanzando a un punto
2M .
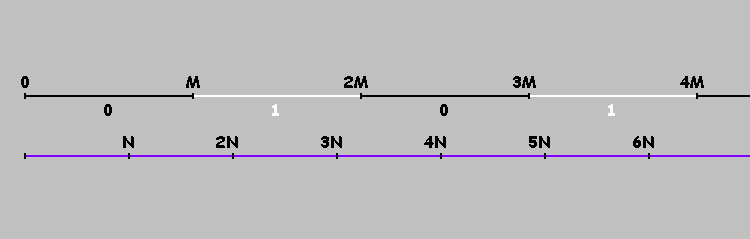
Múltiples
M , dividir nuestro eje en segmentos. Condicionalmente marcamos estos segmentos con unos y ceros (alternando). En los segmentos marcados con ceros, la bola (en un billar rectangular) se mueve de izquierda a derecha. En los segmentos marcados con unidades, de derecha a izquierda. O más simple: la pelota se mueve de izquierda a derecha si
Qk=0 para
Qk= lfloor frac2kNM rfloor( textrmmod2); quadk=0,1,2,...
(Se debe prestar especial atención a esta fórmula. A continuación, volveremos a ella)Es fácil ver que el punto en el que la pelota tocó la pared superior del billar es el resto de la división.
2kN en
M . En este caso, no podemos arreglar el movimiento de la pelota en la dirección opuesta. Tomamos toda la parte de la división.
2kN en
M si es par, consideramos el resto de la división
2kN en
M . Divida el resto resultante por 2 (la distancia entre puntos de contacto adyacentes es de dos celdas). Obtuve los índices de los elementos de la matriz, que necesitamos llenar con ceros. Los elementos restantes se llenan de unidades (la bola se mueve de la pared derecha a la izquierda).
Longitud de secuencia =
fracM2 .
function sequence(m,n){ var md=m/2; var array=[]; for(var k=0;k<md;k++) array[k]=1; for(var k=0;k<md;k++) if(Math.floor(2*k*n/m)%2==0) array[((2*k*n)%m)/2]=0; return array; } console.log(sequence(55, 34).join(''));
Ahora podemos construir una secuencia binaria para billar con cualquier lado
M y
N (por números naturales).
Algunos ejemplos
144x89 (números de Fibonacci):
010100101101001011010110100101101001010010110100101101011010010110100101169x70 (números de Pell):
0101011010100101011010100101011010110101001010110101001010110101001010010101101010010233x55 (números impares de Fibonacci
Fn y
Fn−3 ):
0100100110110110010011011011001001001101100100100110110010010011011011001001101101100
10010011011001001001101100100100Otra mesa interesanteSe obtienen gráficos muy interesantes si toma billar con un ancho
M y construir secuencias para cada
N de
0 antes
M . A continuación, apile estas secuencias.
var array; for(var y=1;y<m;y++){ array=sequence(m,y); for(var x=0;x<array.length;x++){ if(array[x]==0) context.fillRect (x, y, 1, 1); } }
Algunos ejemplos
M = 610:

M = 611:

M = 612:

M = 613:

M = 614:
 Por lo demás M
Por lo demás M Tenemos secuencias ¿De qué otra manera puedes visualizar secuencias binarias? Usando
Turtle Graphics .
Gráficos de tortuga
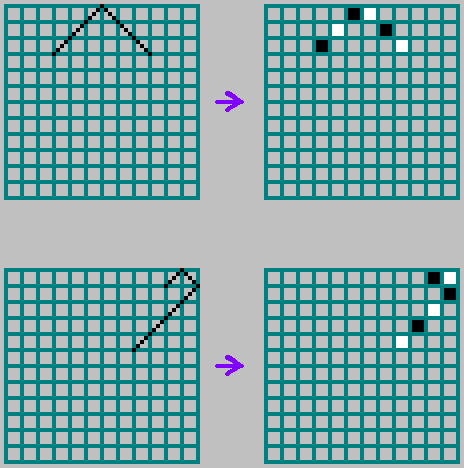
Dibuja una linea. A continuación, tomamos alternativamente los bits de nuestra secuencia. Si bit = 1 - gire el segmento relativo al anterior
60 circ (en sentido horario). Si bit = 0, gire el segmento por
−60 circ . El comienzo del siguiente segmento es el final del anterior.
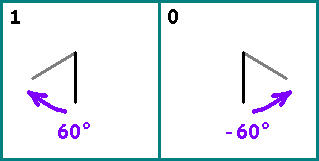
Tome dos números de Fibonacci lo suficientemente grandes:
F29=514229 y
F28=317811 .
Construyó la secuencia:
00101101001011010010100101101001011010110100101101001010010110100101 ... (257114 caracteres más bit cero).
Visualizamos usando gráficos de tortuga. El tamaño del segmento inicial es de 10 píxeles (el segmento inicial en la esquina inferior derecha):

El tamaño del segmento inicial es de 5 píxeles:

El tamaño del segmento inicial es de 1 píxel:

El siguiente ejemplo son los números de Pell.
Pn= begincases0,n=0;1,n=12Pn−1+Pn−2,n>1 endcases
Tomar
P16=470832 y
P15=195025 .
Secuencia:
0010100101011010100101011010100101001010110101001010110101000010101101 (235415 caracteres más bit cero).
El tamaño del segmento inicial es de 1 píxel:
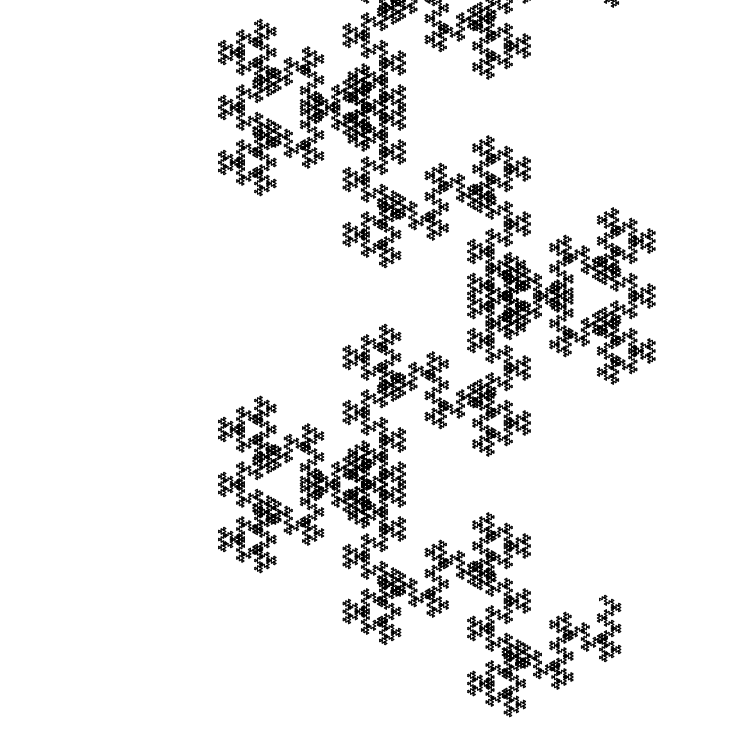
Otro ejemplo son los números impares de Fibonacci
Fn y
Fn−3 .
Tomar
F28=317811 y
F25=75025 .
Secuencia:
00110110010010011111001001001001101101100100110110110010010011011011001001 ... (158905 más bit cero).
En lugar de esquinas
60 circ y
−60 circ usaremos las esquinas
90 circ y
−90 circ .
El tamaño del segmento inicial es de 5 píxeles:

El tamaño del segmento inicial es de 0.4 píxeles:

Esta curva tiene un nombre: "
palabra fractal de Fibonacci ". La dimensión de Hausdorff para esta curva es conocida:
D=3 frac log Phi log(1+ sqrt2)=1,6379; quad Phi= frac1+ sqrt52
Script para visualizar secuencias binarias usando Turtle GraphicsEl problema
¿Es posible dibujar un patrón para el billar, cuyos lados son inconmensurables (uno de los lados es un número irracional)? La tarea no es trivial. Al intentar resolver este problema, nos enfrentaremos a una serie de preguntas:
1. Si las partes son inconmensurables, no podemos pavimentar el billar con celdas del mismo tamaño.
2. Si los lados son inconmensurables, la pelota se reflejará infinitamente y nunca golpeará la esquina.
3. Las secuencias en el billar no se completan en orden, sino al azar.

Las dos primeras preguntas, obviamente, no tienen solución. Pero si hubiera una manera de llenar la secuencia en orden, entonces podríamos, moviéndonos en la secuencia de izquierda a derecha, restaurar el patrón de la manera que usamos anteriormente. Y así ver cómo se ve el patrón en la esquina superior izquierda del billar, cuyos lados son inconmensurables.
Magia negra
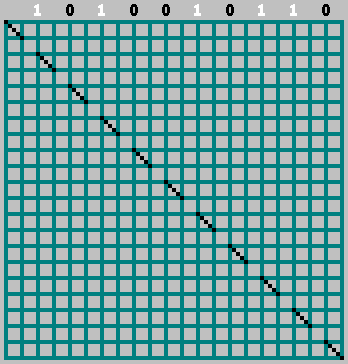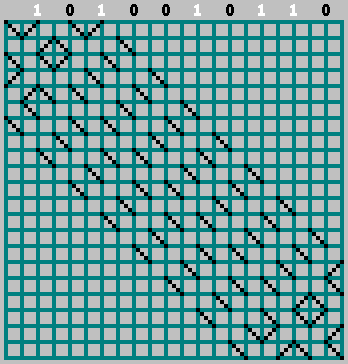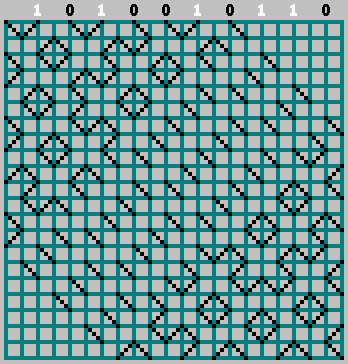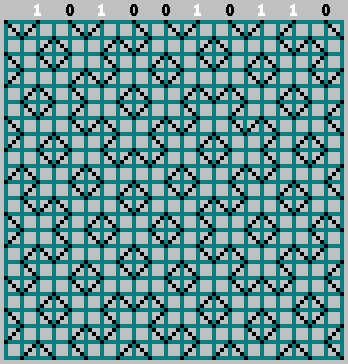
Tome billar, cuyos lados son iguales a los números de Fibonacci (con otros números, tal truco puede no funcionar). Pasa la pelota hacia él y fija el número de la pelota que toca la pared superior. Rellene los números con blanco, si la pelota se movió de derecha a izquierda y negra, si la pelota se movió de izquierda a derecha:

El color blanco corresponde a uno en la secuencia, negro - cero. Ahora arreglemos los números en orden:

Tenemos exactamente la misma secuencia de unos y ceros.
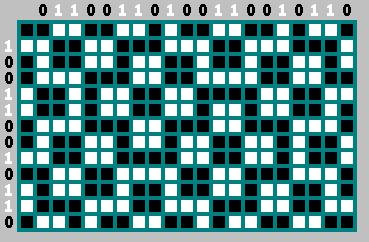
Para otros númerosEl origen es la esquina superior izquierda. A lo largo del eje
x - ancho de billar
M . A lo largo del eje
y - altura de billar
N . Los puntos blancos indican números para los que coinciden las secuencias:

Números para los que se invierte la secuencia:

Subí el
script :

La primera línea son las coordenadas del mouse, que se utilizan como el ancho y la altura de los billares.
La segunda línea son los primeros 100 bits de la secuencia obtenidos a través del resto de la división.
La tercera línea son los primeros 100 bits de la secuencia obtenidos a través de la paridad de la parte entera.
Color negro: renderice la primera secuencia con gráficos de tortuga.
Violeta: visualización de la segunda secuencia.
De hecho, en algunos casos, no necesitamos tomar el resto de la división. Para los números de Fibonacci, es suficiente verificar la paridad de la parte entera de la división
2kN en
M :
Qk= lfloor frac2kNM rfloor( textrmmod2); quadk=0,1,2,...
En el numerador tenemos
Fn . En el denominador -
Fn+1 .
Como sabes:
limn to infty fracFnFn+1= frac1 Phi
Phi - La proporción áurea. Número irracional. Ahora podemos escribir nuestra fórmula como:
Qk= lfloor frac2k Phi rfloor( textrmmod2); quadk=0,1,2,...
Tenemos una fórmula con la que podemos completar la secuencia de billar en orden, cuyo ancho es igual a
Phi y altura
1 . Longitud de secuencia =
infty , pero podemos restaurar parte del patrón, moviéndonos de izquierda a derecha en secuencia y mirando hacia la esquina superior izquierda del billar. Queda por descubrir cómo contar
PhiLa unidad dividida por la proporción áurea se puede reescribir como:
frac1 Phi= frac−1+ sqrt52
Podemos deshacernos de dos:
frac2k Phi= frac2k(−1+ sqrt5)2=k sqrt5−k
Nuestra fórmula toma la forma:
Qk= lfloork sqrt5−k rfloor( textrmmod2); quadk=0,1,2,...
Para mayor claridad, dibujé una mesa. En la tercera columna, descartamos la parte fraccionaria y dejamos el todo. En la cuarta columna, verificamos la paridad de la parte entera:
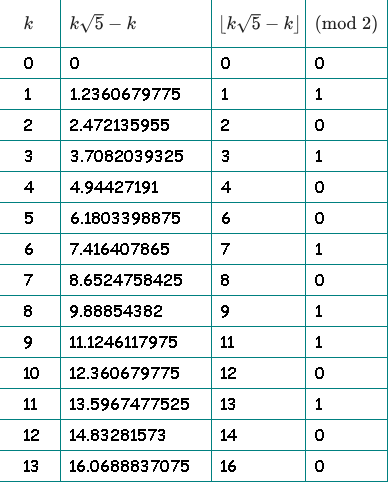
En la cuarta columna tenemos nuestra secuencia: 01010010110100 ...
Seguimos calculando los bits para el resto
k . Restaurando parte del patrón de billar con lados
1 y
Phi :

Si no quitas todo el tiempo
k - entonces cada segundo bit de la secuencia se invierte. Obtenemos la fórmula general:
Qk= lfloork sqrtx rfloor( textrmmod2); quadk=0,1,2,...
¿Qué nos impide usar la raíz cuadrada de tres o, digamos, de dos en lugar de la raíz cuadrada de cinco? Nada
Construimos una secuencia para
k sqrt3+k var x=3; var q=[]; for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x)+k)%2;
Los primeros bits de la secuencia:
00100101101001001011010010110110100101101001001011010010010110100101 ...
Visualizaremos utilizando gráficos de tortuga. Ángulos de 90 y -90 grados. El tamaño del segmento inicial es de 5 píxeles:

El tamaño del segmento inicial es de 0.5 píxeles:

Construimos una secuencia para
k sqrt2 var x=2; var q=[]; for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x))%2;
Los primeros bits de la secuencia (
A083035 ):
01001101100100110010011011001101100100110110011011001001100100110110 ...
Ángulos de 90 y -90 grados. El tamaño del segmento inicial es de 5 píxeles:

El tamaño del segmento inicial es de 0.5 píxeles:

Es interesanteDesde esta curva, puede restaurar el "patrón de billar" y ver qué hay alrededor de la curva:

Sería interesante recoger
M y
N para este patrón
Y estoEl número de segmentos en la parte repetitiva de la curva =
Pn (Pell números: 0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, ...).

sqrt2= limn to infty tfracPn−1+PnPn
Ángulos de 60 y -60 grados. El tamaño del segmento inicial es de 5 píxeles:
 Secuencia de comandos de visualización
Secuencia de comandos de visualizaciónAlguien puede dudar de que la paridad de la parte entera de
k sqrt2 da una secuencia fractal Visualizamos parte de esta secuencia de la segunda manera:

Para mayor claridad, pinté sobre la curva más larga en el patrón resultante:

Esta curva tiene un nombre: "palabra fractal de Fibonacci".
¿Cómo obtener esta secuencia con billar? Tomamos billar, cuyo ancho = 1 y altura =
sqrt2 . En los límites superior e inferior, fijamos la dirección del movimiento de la pelota. Si la pelota se movió de izquierda a derecha, escriba 0, si es de derecha a izquierda, escriba 1.

Dos gráficos:
z= lfloory sqrtx rfloor( textrmmod2)

z= lflooryx sqrt2 rfloor( textrmmod2)

Puede continuar en esta línea durante mucho tiempo: los patrones tienen muchas propiedades interesantes. Pero el artículo ya era demasiado engorroso. Al final hablaré sobre una de las propiedades interesantes.
Al ver imágenes, algunos usuarios pueden experimentar un ataque epiléptico.En billar binario, comenzamos la pelota desde la esquina superior izquierda y llenamos la matriz con bits.
Para billar 610x377:

Parte ampliada del patrón:

Si comienza la segunda bola desde un ángulo diferente (desde la parte inferior izquierda para billar 610x377) y marca los bits que coinciden en ambas trayectorias, obtenemos un patrón muy interesante:

Los bits coincidentes están marcados con píxeles negros. Parte ampliada del patrón:

Hay dos formas más de dibujar este patrón. Uno de ellos fue mencionado en el artículo
Perfect shuffle . Segundo:
Dibujemos una gráfica de la función:
z= sin(x pi( sqrt5+1))+ sin(y pi( sqrt5+1))
Y marca con puntos negros
z<0 :

Parte ampliada del patrón:
