
Durante el desarrollo de
meshoptimizer , a menudo surge la pregunta: "¿Puede este algoritmo usar SIMD?"
La biblioteca está orientada al rendimiento, pero SIMD no siempre proporciona ventajas significativas de velocidad. Desafortunadamente, SIMD puede hacer que el código sea menos portátil y menos mantenible. Por lo tanto, en cada caso, es necesario buscar un compromiso. Cuando el rendimiento es primordial, debe desarrollar y mantener implementaciones SIMD separadas para los conjuntos de instrucciones SSE y NEON. En otros casos, debe comprender cuál es el efecto del uso de SIMD. Hoy intentaremos acelerar el simplificador de mallas descuidado, un nuevo algoritmo recientemente agregado a la biblioteca, usando los conjuntos de instrucciones SSEn / AVXn.
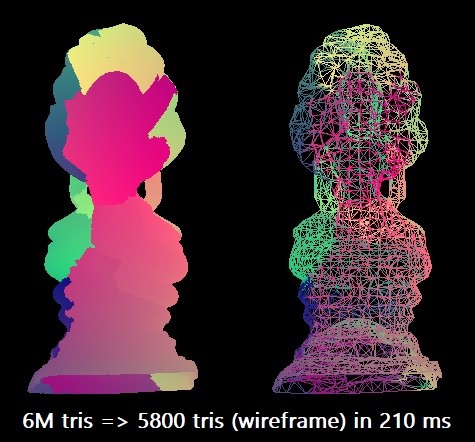
Para nuestro punto de referencia, simplificamos el modelo de Buda tailandés de 6 millones de triángulos al 0.1% de este número. Utilizamos el compilador Microsoft Visual Studio 2019 para la arquitectura x64 de destino. El algoritmo escalar puede realizar tal racionalización en aproximadamente 210 ms en un solo hilo Intel Core i7-8700K (a ~ 4.4 GHz). Esto corresponde a aproximadamente 28.5 millones de triángulos por segundo. Quizás esto sea suficiente en la práctica, pero tenía curiosidad por explorar las capacidades máximas del equipo.
En algunos casos, el procedimiento se puede paralelizar dividiendo la cuadrícula en partes, pero para esto es necesario realizar un análisis adicional de conectividad para mantener los límites, por lo que por ahora nos limitaremos a optimizaciones puramente SIMD.
Siete medidas
Para comprender las posibilidades de optimización, realizaremos la creación de perfiles con Intel VTune. Ejecute el procedimiento 100 veces para asegurarse de que haya suficientes datos.

Aquí activé el modo de microarquitectura para corregir el tiempo de ejecución de cada función, así como para encontrar cuellos de botella. Vemos que la racionalización se realiza utilizando un conjunto de funciones, cada una de las cuales requiere un cierto número de ciclos. La lista de funciones está ordenada por tiempo. Aquí están en orden de ejecución para que el algoritmo sea más fácil de entender:
rescalePositions normaliza las posiciones de todos los vértices en un solo cubo para prepararse para la cuantización usando computeVertexIdscomputeVertexIds calcula un identificador cuantificado de 30 bits para cada vértice en una cuadrícula uniforme de un tamaño dado, donde cada eje se cuantifica en una cuadrícula (tamaño de cuadrícula de 10 bits, por lo que el identificador es 30)countTriangles calcula el número aproximado de triángulos que creará el innovador para un tamaño de cuadrícula dado, suponiendo la unión de todos los vértices en una celda de cuadrículafillVertexCells llena una tabla que fillVertexCells todos los vértices a las celdas correspondientes; todos los vértices con la misma ID corresponden a una celdafillCellQuadrics llena la estructura Quadric (matriz simétrica Quadric ) para cada celda para reflejar información agregada sobre la geometría correspondientefillCellRemap calcula el índice de vértices de cada celda, elige uno de los vértices de esta celda y minimiza la distorsión geométricafilterTriangles muestra el conjunto final de triángulos de acuerdo con las tablas vertex-cell-vertex construidas anteriormente; La traducción ingenua puede producir un promedio de ~ 5% de triángulos duplicados, por lo que la función filtra los duplicados.
computeVertexIds y
countTriangles se ejecutan varias veces: el algoritmo determina el tamaño de malla para fusionar vértices, realiza una búsqueda binaria acelerada para lograr el número objetivo de triángulos (en nuestro caso 6000) y calcula el número de triángulos que generará cada tamaño de malla en cada iteración. Otras funciones se inician una vez. En nuestro archivo, cinco pases de búsqueda dan un tamaño de malla objetivo de 40
3 .
VTune informa útilmente que la función que requiere más recursos es la que calcula los cuádricos: lleva casi la mitad del tiempo de ejecución total de 21 s. Este es el primer objetivo para optimizar SIMD.
SIMD pieza por pieza
Echemos un vistazo al código fuente de
fillCellQuadrics para comprender mejor lo que calcula exactamente:
static void fillCellQuadrics(Quadric* cell_quadrics, const unsigned int* indices, size_t index_count, const Vector3* vertex_positions, const unsigned int* vertex_cells) { for (size_t i = 0; i < index_count; i += 3) { unsigned int i0 = indices[i + 0]; unsigned int i1 = indices[i + 1]; unsigned int i2 = indices[i + 2]; unsigned int c0 = vertex_cells[i0]; unsigned int c1 = vertex_cells[i1]; unsigned int c2 = vertex_cells[i2]; bool single_cell = (c0 == c1) & (c0 == c2); float weight = single_cell ? 3.f : 1.f; Quadric Q; quadricFromTriangle(Q, vertex_positions[i0], vertex_positions[i1], vertex_positions[i2], weight); if (single_cell) { quadricAdd(cell_quadrics[c0], Q); } else { quadricAdd(cell_quadrics[c0], Q); quadricAdd(cell_quadrics[c1], Q); quadricAdd(cell_quadrics[c2], Q); } } }
La función itera sobre todos los triángulos, calcula un cuadrático para cada uno de ellos y lo agrega a los cuádricos de cada celda. Cuadrático: una matriz simétrica 4 × 4, presentada como 10 números de coma flotante:
struct Quadric { float a00; float a10, a11; float a20, a21, a22; float b0, b1, b2, c; };
El cálculo de un cuadrático requiere resolver la ecuación plana para un triángulo, construir una matriz cuadrática y pesarla usando el área del triángulo:
static void quadricFromPlane(Quadric& Q, float a, float b, float c, float d) { Q.a00 = a * a; Q.a10 = b * a; Q.a11 = b * b; Q.a20 = c * a; Q.a21 = c * b; Q.a22 = c * c; Q.b0 = d * a; Q.b1 = d * b; Q.b2 = d * c; Qc = d * d; } static void quadricFromTriangle(Quadric& Q, const Vector3& p0, const Vector3& p1, const Vector3& p2, float weight) { Vector3 p10 = {p1.x - p0.x, p1.y - p0.y, p1.z - p0.z}; Vector3 p20 = {p2.x - p0.x, p2.y - p0.y, p2.z - p0.z}; Vector3 normal = { p10.y * p20.z - p10.z * p20.y, p10.z * p20.x - p10.x * p20.z, p10.x * p20.y - p10.y * p20.x }; float area = normalize(normal); float distance = normal.x*p0.x + normal.y*p0.y + normal.z*p0.z; quadricFromPlane(Q, normal.x, normal.y, normal.z, -distance); quadricMul(Q, area * weight); }
Parece que hay muchas operaciones de coma flotante, por lo que pueden ser paralelas usando SIMD. Primero, representamos cada vector como un vector SIMD de 4 anchos, y también cambiamos la estructura
Quadric a 12 números de coma flotante en lugar de 10 para que se ajuste exactamente en tres registros SIMD (aumentar el tamaño no afecta el rendimiento) y cambiar el orden de los campos para que los cálculos
quadricFromPlane volvió más uniforme:
struct Quadric { float a00, a11, a22; float pad0; float a10, a21, a20; float pad1; float b0, b1, b2, c; };
Aquí, algunos cálculos, en particular el producto escalar, no son muy consistentes con versiones anteriores de SSE. Afortunadamente, apareció una instrucción para un producto escalar en SSE4.1, que es muy útil para nosotros.
static void fillCellQuadrics(Quadric* cell_quadrics, const unsigned int* indices, size_t index_count, const Vector3* vertex_positions, const unsigned int* vertex_cells) { const int yzx = _MM_SHUFFLE(3, 0, 2, 1); const int zxy = _MM_SHUFFLE(3, 1, 0, 2); const int dp_xyz = 0x7f; for (size_t i = 0; i < index_count; i += 3) { unsigned int i0 = indices[i + 0]; unsigned int i1 = indices[i + 1]; unsigned int i2 = indices[i + 2]; unsigned int c0 = vertex_cells[i0]; unsigned int c1 = vertex_cells[i1]; unsigned int c2 = vertex_cells[i2]; bool single_cell = (c0 == c1) & (c0 == c2); __m128 p0 = _mm_loadu_ps(&vertex_positions[i0].x); __m128 p1 = _mm_loadu_ps(&vertex_positions[i1].x); __m128 p2 = _mm_loadu_ps(&vertex_positions[i2].x); __m128 p10 = _mm_sub_ps(p1, p0); __m128 p20 = _mm_sub_ps(p2, p0); __m128 normal = _mm_sub_ps( _mm_mul_ps( _mm_shuffle_ps(p10, p10, yzx), _mm_shuffle_ps(p20, p20, zxy)), _mm_mul_ps( _mm_shuffle_ps(p10, p10, zxy), _mm_shuffle_ps(p20, p20, yzx))); __m128 areasq = _mm_dp_ps(normal, normal, dp_xyz);
No hay nada particularmente interesante en este código; Estamos utilizando abundantemente las instrucciones de carga / almacenamiento sin alinear. Aunque la entrada de Vector3 se puede alinear, parece que no hay penalización notable para las lecturas no alineadas. Tenga en cuenta que en la primera mitad de la función no se utilizan vectores, lo cual es bueno: nuestros vectores tienen tres componentes y, en algunos casos, solo uno (consulte el cálculo de áreas q / área / distancia), mientras que el procesador realiza 4 operaciones en paralelo. En cualquier caso, veamos cómo ha ayudado la paralelización.

Cien inicios de
fillCellQuadrics ahora se ejecutan en 5.3 s en lugar de 9.8 s, lo que ahorra aproximadamente 45 ms en cada operación, no está mal, pero no es muy impresionante. En muchas instrucciones, utilizamos tres componentes en lugar de cuatro, así como la multiplicación precisa, lo que produce un retraso bastante significativo. Si anteriormente escribió instrucciones para SIMD, entonces sabe cómo hacer el producto escalar correctamente.
Para hacer esto, necesitas hacer cuatro vectores a la vez. En lugar de almacenar un vector completo en un registro SIMD, utilizamos tres registros: en uno almacenamos cuatro componentes de
x , en el otro almacenaremos
, y en el tercero
z . Aquí se necesitan cuatro vectores para trabajar a la vez: eso significa que procesaremos cuatro triángulos simultáneamente.
Tenemos muchos arreglos con indexación dinámica. Por lo general, ayuda transferir datos a matrices preparadas de componentes
x /
y /
z (o mejor dicho, generalmente se usan registros SIMD pequeños, por ejemplo,
float x[8], y[8], z[8] , para cada uno de los 8 vértices en la entrada datos: esto se llama AoSoA (matrices de estructuras de matrices) y proporciona un buen equilibrio entre la ubicación de la memoria caché y la facilidad de carga en los registros SIMD), pero aquí la indexación dinámica no funcionará muy bien, así que cargue los datos para cuatro triángulos como de costumbre y transponga los vectores usando un conveniente macro
_MM_TRANSPOSE .
Teóricamente, debe calcular cada componente de cuatro cuádricas finitas en su propio registro SIMD (por ejemplo, tendremos
__m128 Q_a00 con cuatro componentes de cuatro
a00 finitas). En este caso, las operaciones en los cuádricos encajan bastante bien en las instrucciones SIMD de 4 anchos, y la conversión en realidad ralentiza el código; por lo tanto, transponemos solo los vectores iniciales, y luego transponemos las ecuaciones planas y ejecutamos el mismo código que usamos para calcular los cuádricos, pero lo repetimos cuatro veces Aquí está el código que luego calcula las ecuaciones del plano (las partes restantes se omiten por brevedad):
unsigned int i00 = indices[(i + 0) * 3 + 0]; unsigned int i01 = indices[(i + 0) * 3 + 1]; unsigned int i02 = indices[(i + 0) * 3 + 2]; unsigned int i10 = indices[(i + 1) * 3 + 0]; unsigned int i11 = indices[(i + 1) * 3 + 1]; unsigned int i12 = indices[(i + 1) * 3 + 2]; unsigned int i20 = indices[(i + 2) * 3 + 0]; unsigned int i21 = indices[(i + 2) * 3 + 1]; unsigned int i22 = indices[(i + 2) * 3 + 2]; unsigned int i30 = indices[(i + 3) * 3 + 0]; unsigned int i31 = indices[(i + 3) * 3 + 1]; unsigned int i32 = indices[(i + 3) * 3 + 2];
El código se ha vuelto un poco más largo: ahora procesamos cuatro triángulos en cada iteración, y ya no necesitamos instrucciones SSE4.1 para esto. En teoría, las unidades SIMD deberían usarse de manera más eficiente. Veamos cómo ayudó.

Está bien, está bien. El código se ha acelerado muy ligeramente, aunque la función
fillCellQuadrics ahora se ejecuta casi el doble de rápido que la función original sin SIMD, pero no está claro si esto justifica un aumento significativo en la complejidad. Teóricamente, puede usar AVX2 y procesar 8 triángulos por iteración, pero aquí necesitará girar aún más el bucle manualmente (idealmente, todo este código se genera utilizando ISPC, pero mis ingenuos intentos para que genere un buen código no tuvieron éxito: en lugar de cargar / almacenar secuencias él persistentemente emitió una reunión / dispersión, lo que ralentiza significativamente la ejecución). Probemos algo más.
AVX2 = SSE2 + SSE2
El AVX2 es un conjunto de instrucciones. Tiene 8 registros de punto flotante de ancho, y una instrucción puede realizar 8 operaciones; pero, en esencia, dicha instrucción no difiere de dos instrucciones SSE2 ejecutadas en dos mitades del registro (por lo que entiendo, los primeros procesadores con soporte AVX2 decodificaron cada instrucción en dos o más microoperaciones, por lo tanto, la ganancia de rendimiento estuvo limitada por la fase de extracción de instrucciones). Por ejemplo,
_mm_dp_ps realiza un producto escalar entre dos registros SSE2, y
_mm256_dp_ps produce dos productos escalares entre dos mitades de dos registros AVX2, por lo tanto, está limitado a 4 de ancho por cada mitad.
Debido a esto, el código AVX2 a menudo difiere del "SIMD de 8 anchos" universal, pero aquí funciona a nuestro favor: en lugar de tratar de mejorar la vectorización mediante la transposición de vectores de 4 anchos, volvemos a la primera versión de SIMD y duplicamos el bucle usando instrucciones AVX2 en lugar de SSE2 / SSE4. Todavía necesitamos cargar y almacenar vectores de 4 anchos, pero en general, simplemente cambiamos
__m128 a
__m256 y
_mm_ a
_mm256 en el
_mm256 con varias configuraciones:
unsigned int i00 = indices[(i + 0) * 3 + 0]; unsigned int i01 = indices[(i + 0) * 3 + 1]; unsigned int i02 = indices[(i + 0) * 3 + 2]; unsigned int i10 = indices[(i + 1) * 3 + 0]; unsigned int i11 = indices[(i + 1) * 3 + 1]; unsigned int i12 = indices[(i + 1) * 3 + 2]; __m256 p0 = _mm256_loadu2_m128( &vertex_positions[i10].x, &vertex_positions[i00].x); __m256 p1 = _mm256_loadu2_m128( &vertex_positions[i11].x, &vertex_positions[i01].x); __m256 p2 = _mm256_loadu2_m128( &vertex_positions[i12].x, &vertex_positions[i02].x); __m256 p10 = _mm256_sub_ps(p1, p0); __m256 p20 = _mm256_sub_ps(p2, p0); __m256 normal = _mm256_sub_ps( _mm256_mul_ps( _mm256_shuffle_ps(p10, p10, yzx), _mm256_shuffle_ps(p20, p20, zxy)), _mm256_mul_ps( _mm256_shuffle_ps(p10, p10, zxy), _mm256_shuffle_ps(p20, p20, yzx))); __m256 areasq = _mm256_dp_ps(normal, normal, dp_xyz); __m256 area = _mm256_sqrt_ps(areasq); __m256 areanz = _mm256_cmp_ps(area, _mm256_setzero_ps(), _CMP_NEQ_OQ); normal = _mm256_and_ps(_mm256_div_ps(normal, area), areanz); __m256 distance = _mm256_dp_ps(normal, p0, dp_xyz); __m256 negdistance = _mm256_sub_ps(_mm256_setzero_ps(), distance); __m256 normalnegdist = _mm256_blend_ps(normal, negdistance, 0x88); __m256 Qx = _mm256_mul_ps(normal, normal); __m256 Qy = _mm256_mul_ps( _mm256_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 2, 2, 1)), _mm256_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 0, 1, 0))); __m256 Qz = _mm256_mul_ps(negdistance, normalnegdist);
Aquí puede tomar cada mitad de 128 bits de los
Qz /
Qz /
Qz y ejecutar el mismo código que usamos para agregar los cuádricos. En cambio, suponemos que si un triángulo tiene tres vértices en una celda (
single_cell == true ), entonces es muy probable que otro triángulo tenga tres vértices en otra celda, y también realizamos la agregación final de cuádricos usando AVX2:
unsigned int c00 = vertex_cells[i00]; unsigned int c01 = vertex_cells[i01]; unsigned int c02 = vertex_cells[i02]; unsigned int c10 = vertex_cells[i10]; unsigned int c11 = vertex_cells[i11]; unsigned int c12 = vertex_cells[i12]; bool single_cell = (c00 == c01) & (c00 == c02) & (c10 == c11) & (c10 == c12); if (single_cell) { area = _mm256_mul_ps(area, _mm256_set1_ps(3.f)); Qx = _mm256_mul_ps(Qx, area); Qy = _mm256_mul_ps(Qy, area); Qz = _mm256_mul_ps(Qz, area); Quadric& q00 = cell_quadrics[c00]; Quadric& q10 = cell_quadrics[c10]; __m256 q0x = _mm256_loadu2_m128(&q10.a00, &q00.a00); __m256 q0y = _mm256_loadu2_m128(&q10.a10, &q00.a10); __m256 q0z = _mm256_loadu2_m128(&q10.b0, &q00.b0); _mm256_storeu2_m128(&q10.a00, &q00.a00, _mm256_add_ps(q0x, Qx)); _mm256_storeu2_m128(&q10.a10, &q00.a10, _mm256_add_ps(q0y, Qy)); _mm256_storeu2_m128(&q10.b0, &q00.b0, _mm256_add_ps(q0z, Qz)); } else {
El código resultante es más simple, conciso y más rápido que nuestro enfoque fallido SSE2:

Por supuesto, no logramos una aceleración de 8 veces, sino solo 2,45 veces. Las operaciones de carga y almacenamiento siguen siendo de 4 anchos, ya que nos vemos obligados a trabajar con un diseño de memoria incómodo debido a la indexación dinámica, y los cálculos no son óptimos para SIMD. Pero ahora
fillCellQuadrics no es el cuello de botella en nuestra línea de perfiles, y puede concentrarse en otras funciones.
Reúnase, niños
Ahorramos 4.8 segundos en la ejecución de prueba (48 ms en cada ejecución), y ahora nuestro intruso principal es
countTriangles . Parecería ser una función simple, pero se ejecuta no una, sino cinco veces:
static size_t countTriangles(const unsigned int* vertex_ids, const unsigned int* indices, size_t index_count) { size_t result = 0; for (size_t i = 0; i < index_count; i += 3) { unsigned int id0 = vertex_ids[indices[i + 0]]; unsigned int id1 = vertex_ids[indices[i + 1]]; unsigned int id2 = vertex_ids[indices[i + 2]]; result += (id0 != id1) & (id0 != id2) & (id1 != id2); } return result; }
La función itera sobre todos los triángulos de origen y calcula el número de triángulos no degenerados comparando los identificadores de los vértices. No está claro de inmediato cómo paralelizarlo usando SIMD ... a menos que use las instrucciones de recopilación.
El conjunto de instrucciones AVX2 ha agregado la familia de instrucciones de recopilación / dispersión al SIMD x64; cada uno de ellos toma un registro vectorial con 4 u 8 valores, y simultáneamente realiza 4 u 8 operaciones de carga o guardado. Si usa el método de recopilación aquí, puede descargar tres índices, ejecutar la recopilación para todos a la vez (o en grupos de 4 u 8) y comparar los resultados. La recopilación de procesadores Intel ha sido históricamente bastante lenta, pero probémoslo. Para simplificar, cargamos datos para 8 triángulos, transponemos vectores de manera similar a nuestro intento anterior y comparamos los elementos correspondientes de cada vector:
for (size_t i = 0; i < (triangle_count & ~7); i += 8) { __m256 tri0 = _mm256_loadu2_m128( (const float*)&indices[(i + 4) * 3 + 0], (const float*)&indices[(i + 0) * 3 + 0]); __m256 tri1 = _mm256_loadu2_m128( (const float*)&indices[(i + 5) * 3 + 0], (const float*)&indices[(i + 1) * 3 + 0]); __m256 tri2 = _mm256_loadu2_m128( (const float*)&indices[(i + 6) * 3 + 0], (const float*)&indices[(i + 2) * 3 + 0]); __m256 tri3 = _mm256_loadu2_m128( (const float*)&indices[(i + 7) * 3 + 0], (const float*)&indices[(i + 3) * 3 + 0]); _MM_TRANSPOSE8_LANE4_PS(tri0, tri1, tri2, tri3); __m256i i0 = _mm256_castps_si256(tri0); __m256i i1 = _mm256_castps_si256(tri1); __m256i i2 = _mm256_castps_si256(tri2); __m256i id0 = _mm256_i32gather_epi32((int*)vertex_ids, i0, 4); __m256i id1 = _mm256_i32gather_epi32((int*)vertex_ids, i1, 4); __m256i id2 = _mm256_i32gather_epi32((int*)vertex_ids, i2, 4); __m256i deg = _mm256_or_si256( _mm256_cmpeq_epi32(id1, id2), _mm256_or_si256( _mm256_cmpeq_epi32(id0, id1), _mm256_cmpeq_epi32(id0, id2))); result += 8 - _mm_popcnt_u32(_mm256_movemask_epi8(deg)) / 4; }
La macro
_MM_TRANSPOSE8_LANE4_PS en AVX2 es el equivalente de
_MM_TRANSPOSE4_PS , que no se encuentra en el encabezado estándar, pero se muestra fácilmente. Toma cuatro vectores AVX2 y transpone dos matrices 4 × 4 independientemente una de la otra:
#define _MM_TRANSPOSE8_LANE4_PS(row0, row1, row2, row3) \ do { \ __m256 __t0, __t1, __t2, __t3; \ __t0 = _mm256_unpacklo_ps(row0, row1); \ __t1 = _mm256_unpackhi_ps(row0, row1); \ __t2 = _mm256_unpacklo_ps(row2, row3); \ __t3 = _mm256_unpackhi_ps(row2, row3); \ row0 = _mm256_shuffle_ps(__t0, __t2, _MM_SHUFFLE(1, 0, 1, 0)); \ row1 = _mm256_shuffle_ps(__t0, __t2, _MM_SHUFFLE(3, 2, 3, 2)); \ row2 = _mm256_shuffle_ps(__t1, __t3, _MM_SHUFFLE(1, 0, 1, 0)); \ row3 = _mm256_shuffle_ps(__t1, __t3, _MM_SHUFFLE(3, 2, 3, 2)); \ } while (0)
Debido a algunas características en los conjuntos de instrucciones SSE2 / AVX2, debemos usar operaciones de registro de punto flotante al transponer vectores. Estamos cargando los datos un poco descuidadamente; pero básicamente no importa, porque el rendimiento de recopilación nos limita:

Ahora
countTriangles es aproximadamente un 27% más rápido y nota el terrible IPC (ciclos por instrucción): enviamos unas cuatro veces menos instrucciones, pero reunirlas lleva mucho tiempo. Es genial que acelere el trabajo general, pero, por supuesto, la ganancia de rendimiento es algo deprimente. Logramos superar a
fillCellQuadrics en el perfil, lo que nos lleva a la última función en la parte superior de la lista, que aún no hemos visto.
Capítulo 6, donde todo comienza a funcionar como debería
La última función es
computeVertexIds . En el algoritmo, se realiza 6 veces, por lo tanto, también representa un excelente objetivo para la optimización. Por primera vez, vemos una función que parece haber sido creada para una optimización clara en SIMD:
static void computeVertexIds(unsigned int* vertex_ids, const Vector3* vertex_positions, size_t vertex_count, int grid_size) { assert(grid_size >= 1 && grid_size <= 1024); float cell_scale = float(grid_size - 1); for (size_t i = 0; i < vertex_count; ++i) { const Vector3& v = vertex_positions[i]; int xi = int(vx * cell_scale + 0.5f); int yi = int(vy * cell_scale + 0.5f); int zi = int(vz * cell_scale + 0.5f); vertex_ids[i] = (xi << 20) | (yi << 10) | zi; } }
Después de las optimizaciones anteriores, sabemos qué hacer: desenrollar el ciclo 4 u 8 veces, ya que no tiene sentido intentar acelerar solo una iteración, transponer los componentes del vector y ejecutar los cálculos en paralelo. Hagámoslo con AVX2, procesando 8 vértices a la vez:
__m256 scale = _mm256_set1_ps(cell_scale); __m256 half = _mm256_set1_ps(0.5f); for (size_t i = 0; i < (vertex_count & ~7); i += 8) { __m256 vx = _mm256_loadu2_m128( &vertex_positions[i + 4].x, &vertex_positions[i + 0].x); __m256 vy = _mm256_loadu2_m128( &vertex_positions[i + 5].x, &vertex_positions[i + 1].x); __m256 vz = _mm256_loadu2_m128( &vertex_positions[i + 6].x, &vertex_positions[i + 2].x); __m256 vw = _mm256_loadu2_m128( &vertex_positions[i + 7].x, &vertex_positions[i + 3].x); _MM_TRANSPOSE8_LANE4_PS(vx, vy, vz, vw); __m256i xi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vx, scale), half)); __m256i yi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vy, scale), half)); __m256i zi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vz, scale), half)); __m256i id = _mm256_or_si256( zi, _mm256_or_si256( _mm256_slli_epi32(xi, 20), _mm256_slli_epi32(yi, 10))); _mm256_storeu_si256((__m256i*)&vertex_ids[i], id); }
Y mira los resultados: aceleramos
aceleramos computeVertexIdsdos veces. Teniendo en cuenta todas las optimizaciones, el tiempo total de ejecución del programa se redujo a aproximadamente 120 ms, lo que corresponde al cálculo de 50 millones de triángulos por segundo.Puede parecer que nuevamente no logramos el crecimiento esperado de la productividad: ¿ computeVertexIdsno debería acelerarse más de dos veces después de la paralelización? Para responder a esta pregunta, intentemos ver cuánto trabajo realiza esta función.computeVertexIdsse ejecuta seis veces para el inicio de un programa: cinco veces durante la búsqueda binaria y una vez al final para calcular los identificadores finales que se utilizan para el procesamiento posterior. Cada vez que esta función procesa 3 millones de vértices, lee 12 bytes para cada vértice y escribe 4 bytes.En total, más de 100 ejecuciones del innovador, esta función procesa 1.800 millones de vértices, lee 21 GB y escribe 7 GB. El procesamiento de 28 GB en 1,46 segundos requiere un ancho de banda de bus de 19 GB / s. Podemos verificar el ancho de banda de la memoria ejecutando memcmp(block1, block2, 512 MB). El resultado es de 45 ms, es decir, aproximadamente 22 GB / s en un núcleo (aunque el benchmark AIDA64 muestra velocidades de lectura en mi sistema de hasta 31 GB / s, pero usa varios núcleos). De hecho, nos hemos acercado al límite de memoria máximo alcanzable, y un aumento adicional en el rendimiento requerirá un empaquetamiento más cercano de estos vértices para que ocupen menos de 12 bytes.Conclusión
Tomamos un algoritmo bastante optimizado que simplifica las cuadrículas muy grandes a una velocidad de 28 millones de triángulos por segundo, y utilizamos los conjuntos de instrucciones SSE y AVX para acelerarlo casi dos veces, a 50 millones de triángulos por segundo. Durante este viaje, tuvimos que aprender diferentes formas de usar SIMD: registros para almacenar vectores de 3 anchos, transposición de SoA, instrucciones AVX2 para almacenar dos vectores de 3 anchos, recopilar instrucciones para acelerar la carga de datos en comparación con las instrucciones escalares, y finalmente aplicamos directamente AVX2 para el procesamiento de transmisión.SIMD a menudo no es el mejor punto de partida para la optimización: el racionalizador de malla ha pasado por muchas iteraciones de optimización algorítmica y microoptimización sin usar instrucciones específicas de la plataforma. Pero en algún momento, estas posibilidades están agotadas, y si el rendimiento es crítico, entonces SIMD es una herramienta fantástica que se puede usar si es necesario.No estoy seguro de cuál de estas optimizaciones caerá en la rama principal meshoptimizer: al final, esto es solo un experimento para ver cuánto el overclocking del código sin un cambio fundamental en los algoritmos. Espero que el artículo sea informativo y le brinde ideas para optimizar el código. Las fuentes finales para este artículo están aquí ; este trabajo se basa en la versión de meshoptimizer 99ab49, y el modelo de Buda tailandés se publica en Sketchfab .