🎢 🕕 💴 Optimización del sistema de control LQR 🧛 💦 ⚙️

Introduccion

Se han publicado varios artículos [1,2,3] en Habr que se relacionan directa o indirectamente con este tema. A este respecto, uno no puede dejar de notar la publicación [1] con el título "Matemáticas en los dedos: regulador lineal-cuadrático", que popularmente explica el principio de funcionamiento del controlador LQR óptimo.

Quería continuar con este tema, habiendo examinado la aplicación práctica del método de optimización dinámica, pero ya en un ejemplo concreto usando Python. Primero, algunas palabras sobre la terminología y el método de optimización dinámica.

Los métodos de optimización se dividen en estáticos y dinámicos. El objeto de control está en un estado de movimiento continuo bajo la influencia de varios factores externos e internos. Por lo tanto, la evaluación del resultado del control se da para el tiempo de control T, y esta es la tarea de la optimización dinámica.

Usando métodos de optimización dinámica, se resuelven los problemas asociados con la distribución de recursos limitados durante un período de tiempo, y la función objetivo se escribe como una función integral.

El aparato matemático para resolver tales problemas son métodos variacionales: cálculo clásico de variaciones, el principio de máxima L.S. Pontryagin y programación dinámica R. Bellman.

El análisis y síntesis de los sistemas de control se realiza en los espacios de tiempo, frecuencia y estado. El análisis y la síntesis de los sistemas de control en el espacio de estado se introduce en el plan de estudios, sin embargo, las técnicas presentadas en los materiales de capacitación que usan el controlador SQR están diseñadas para usar Matlab y no contienen ejemplos prácticos de análisis.

El propósito de esta publicación es considerar los métodos de análisis y síntesis de los sistemas de control lineal en el espacio de estado utilizando el conocido ejemplo de optimización del sistema de control de un motor eléctrico y una aeronave utilizando el lenguaje de programación Python.

Sustanciación matemática del método de optimización dinámica.

Para la optimización, se utilizan los criterios de amplitud (MO), simétricos (CO) y óptimos de compromiso (KO).

Al resolver problemas de optimización en el espacio de estados, un sistema estacionario lineal viene dado por ecuaciones matriciales de vectores:

d o t x = f r a c d x d t = A c d o t x + B c d o t u; y = C c d o t x,

$\ dot {x} = \ frac {dx} {dt} = A \ cdot x + B \ cdot u; y = C \ cdot x,$ (1)

Los criterios integrales para el consumo mínimo de energía de control y la velocidad máxima son establecidos por los funcionales:

J_{x} = i n t_{0}^{i n f t y} (x^{T} Q x + u^{T} R u + 2 x^{T} N u) d t r i g h t a r r o w m i n,

$J_ {x} = \ int_ {0} ^ {\ infty} (x ^ {T} Qx + u ^ {T} Ru + 2x ^ {T} Nu) dt \ rightarrow min,$ (2)

J_{u} = i n t_{0}^{i n f t y} (y^{T} Q y + u^{T} R u + 2 y^{T} N u) d t r i g h t a r r o w m i n . $

$J_ {u} = \ int_ {0} ^ {\ infty} (y ^ {T} Qy + u ^ {T} Ru + 2y ^ {T} Nu) dt \ rightarrow min. $$ (3)

La ley de control u tiene forma de retroalimentación lineal sobre las variables de estado x o sobre las variables de salida y:

u = p m K x, u = p m K y

$u = \ pm Kx, u = \ pm Ky$

Tal control minimiza los criterios de calidad cuadráticos (2), (3). En las relaciones (1) ÷ (3), Q y R son matrices simétricas positivas definidas de dimensión [n × n] y [m × m], respectivamente; K es una matriz de coeficientes constantes de dimensión [m × n], cuyos valores no están limitados. Si se omite el parámetro de entrada N, se toma como cero.

La solución a este problema, que se llama problema de optimización cuadrática integral lineal (optimización LQR), en el espacio de estado está determinada por la expresión:

u = R^{- 1} B^{T} P x

$u = R ^ {- 1} B ^ {T} Px$

donde la matriz P debe satisfacer la ecuación de Ricatti:

A^{T} P + P A + P B R^{- 1} B^{T} P + Q = 0

$A ^ {T} P + PA + PBR ^ {- 1} B ^ {T} P + Q = 0$

Los criterios (2), (3) también son contradictorios, ya que la implementación del primer término requiere una fuente de potencia infinitamente alta y, para el segundo, una fuente de potencia infinitamente baja. Esto puede explicarse por la siguiente expresión:

J_{x} = i n t_{0}^{i n f t y} x^{T} Q x d t

$J_ {x} = \ int_ {0} ^ {\ infty} x ^ {T} Qxdt$ ,

cual es la norma

M o d (x)

$Mod (x)$ vector x, es decir una medida de su oscilación en el proceso de regulación y, por lo tanto, toma valores más pequeños en transitorios rápidos con menos oscilación, y la expresión:

J_{u} = i n t_{0}^{i n f t y} u^{T} R u d t

$J_ {u} = \ int_ {0} ^ {\ infty} u ^ {T} Rudt$

es una medida de la cantidad de energía utilizada para el control; es una penalización por los costos de energía del sistema.

Las matrices de peso Q, R y N dependen de las restricciones de las coordenadas correspondientes. Si algún elemento de estas matrices es igual a cero, la coordenada correspondiente no tiene restricciones. En la práctica, la elección de los valores de las matrices Q, R, N se realiza mediante el método de estimaciones de expertos, ensayos, errores y depende de la experiencia y el conocimiento del ingeniero de diseño.

Para resolver estos problemas, se utilizaron los siguientes operadores de MATLAB:

b e g i n b m a t r i x R, S, E e n d b m a t r i x = l q r (A, B, Q, R, N)

$\ begin {bmatrix} R, S, E \ end {bmatrix} = lqr (A, B, Q, R, N)$ y

b e g i n b m a t r i x R, S, E e n d b m a t r i x = l q r y (P_{s}, Q, R, N)

$\ begin {bmatrix} R, S, E \ end {bmatrix} = lqry (P_ {s}, Q, R, N)$ que minimizan los funcionales (2), (3) por el vector de estado x o por el vector de salida y.

Modelo de objeto de gestión

P_{s} = s s (A, B, C, D) .

$P_ {s} = ss (A, B, C, D).$ El resultado del cálculo es la matriz K de retroalimentaciones óptimas con respecto a las variables de estado x, la solución de la ecuación de Ricatti S y los valores propios E = eiq (A-BK) del sistema de control de circuito cerrado.

Componentes funcionales:

J_{x} = x 0^{T} P_{1} x 0, J_{u} = x 0^{T} P_{2} x 0

$J_ {x} = x0 ^ {T} P_ {1} x0, J_ {u} = x0 ^ {T} P_ {2} x0$

donde x0 es el vector de las condiciones iniciales;

P_{1}

$P_ {1}$ y

P_{2}

$P_ {2}$ - matrices desconocidas que son una solución de las ecuaciones matriciales de Lyapunov. Se encuentran usando funciones;

P_{1} = l y a p (N N, Q)

$P_ {1} = lyap (NN, Q)$ y

P_{2} = l y a p (N N, K^{T} R K)

$P_ {2} = lyap (NN, K ^ {T} RK)$ ,

N N = (A + B K)^{T}

$NN = (A + BK) ^ {T}$

Características de la implementación del método de optimización dinámica usando Python

Aunque la Python Control Systems Library [4] tiene funciones: control.lqr, control.lyap, el uso de control.lqr solo es posible si está instalado el módulo slycot, lo cual es un problema [5]. Cuando se utiliza la función lyap en el contexto de una tarea, la optimización da como resultado un control.exception.ControlArgument: Q debe ser un error de matriz simétrica [6].

Por lo tanto, para implementar las funciones lqr () y lyap (), utilicé scipy.linalg:

from numpy import* from scipy.linalg import* def lqr(A,B,Q,R): S =matrix(solve_continuous_are(A, B, Q, R)) K = matrix(inv(R)*(BT*S)) E= eig(AB*K)[0] return K, S, E P1=solve_lyapunov(NN,Ct*Q*C)

Por cierto, no debe abandonar por completo el control, ya que las funciones step (), pole (), ss (), tf (), feedback (), acker (), place () y otras funcionan bien.

Un ejemplo de optimización de LQR en un accionamiento eléctrico

(se toma un ejemplo de la publicación [7])

Considere la síntesis de un controlador lineal-cuadrático que satisfaga el criterio (2) para un objeto de control definido en el espacio de estado por matrices:

A = \ begin {bmatrix} & -100 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 \\ & 0 & 1.046 & 0 \ end {bmatrix}; B = \ begin {bmatrix} 2300 \\ 0 \\ 0 \\\ end {bmatrix}; C = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}; D = 0

$A = \ begin {bmatrix} & -100 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 \\ & 0 & 1.046 & 0 \ end {bmatrix}; B = \ begin {bmatrix} 2300 \\ 0 \\ 0 \\\ end {bmatrix}; C = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}; D = 0$

Las siguientes son consideradas como variables de estado:

x_{1}

$x_ {1}$ - voltaje del convertidor, V;

x_{2}

$x_ {2}$ - corriente del motor, A;

x_{3}

$x_ {3}$ - velocidad angular

c^{- 1}

$c ^ {- 1}$ . Este es el sistema TP - DPT con HB: motor R nom = 30 kW; Unom = 220 V; Inom = 147 A ;;

o m e g a ω

$\ omega ω$ 0 = 169

c^{- 1}

$c ^ {- 1}$ ;

o m e g a ω

$\ omega ω$ max = 187

c^{- 1}

$c ^ {- 1}$ ; momento de resistencia nominal Mnom = 150 N * m; multiplicidad de corriente de arranque = 2; convertidor de tiristores: Unom = 230 V; Uy = 10 B; Inom = 300 A; multiplicidad de sobrecorriente a corto plazo = 1.2.

Al resolver el problema, aceptamos la matriz Q diagonal. Como resultado del modelado, se encontró que los valores mínimos de los elementos de la matriz R = 84, y

Q = [[0.01, 0, 0], [0, 0.01, 0], [0, 0, 0.01]] .

$Q = [[0.01,0,0], [0, 0.01,0], [0,0,0.01]].$ En este caso, se observa un proceso de transición monotónica de la velocidad angular del motor (Fig. 1). En R = 840

Q = [[0.01, 0, 0], [0, 0.01, 0], [0, 0, 0.01]]

$Q = [[0.01,0,0], [0, 0.01,0], [0,0,0.01]]$ proceso transitorio (Fig. 2) cumple con el criterio MO. El cálculo de las matrices P1 y P2 se realizó en x0 = [220 147 162].

Listado del programa (Fig. 1).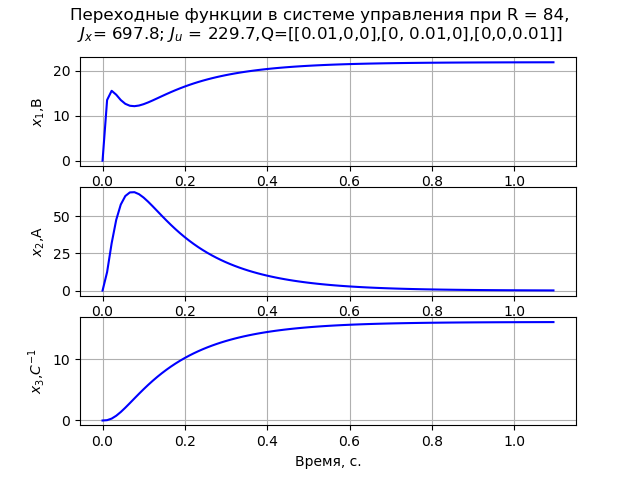

 # -*- coding: utf8 -*- from numpy import* from control.matlab import * from matplotlib import pyplot as plt from scipy.linalg import* def lqr(A,B,Q,R): S =matrix(solve_continuous_are(A, B, Q, R)) K = matrix(inv(R)*(BT*S)) E= eig(AB*K)[0] return K, S, E #   A=matrix([[-100,0,0],[143.678, -16.667,-195.402],[0,1.046,0]]); B=matrix([[2300], [0], [0]]); C=eye(3) D=zeros([3,1]) #    R=[[84]] Q=matrix([[0.01, 0, 0],[0, 0.01, 0],[0, 0, 0.01]]); #  LQR-  [K,S,E]=lqr(A,B,Q,R) #    N=AB*K; NN=NT; w=ss(N,B,C,D) x0=matrix([[220], [147], [162]]); Ct=CT; P1=solve_lyapunov(NN,Ct*Q*C) Kt=KT; x0t=x0.T; Jx=abs((x0t*P1*x0)[0,0]) P2=solve_lyapunov(NN,Kt*R*K); Ju=abs((x0t*P2*x0)[0,0]) fig = plt.figure() plt.suptitle('      R = %s,\n\ $J_{x}$= %s; $J_{u}$ = %s,Q=[[0.01,0,0],[0, 0.01,0],[0,0,0.01]]'%(R[0][0],round(Jx,1),round(Ju,1))) ax1 = fig.add_subplot(311) y,x=step(w[0,0]) ax1.plot(x,y,"b") plt.ylabel('$x_{1}$,B') ax1.grid(True) ax2 = fig.add_subplot(312) y,x=step(w[1,0]) ax2.plot(x,y,"b") plt.ylabel('$x_{2}$,A') ax2.grid(True) ax3 = fig.add_subplot(313) y,x=step(w[2,0]) ax3.plot(x,y,"b") plt.ylabel('$x_{3}$,$C^{-1}$') ax3.grid(True) plt.xlabel(', .') plt.show()

Fig. 1

Listado del programa (Fig. 2).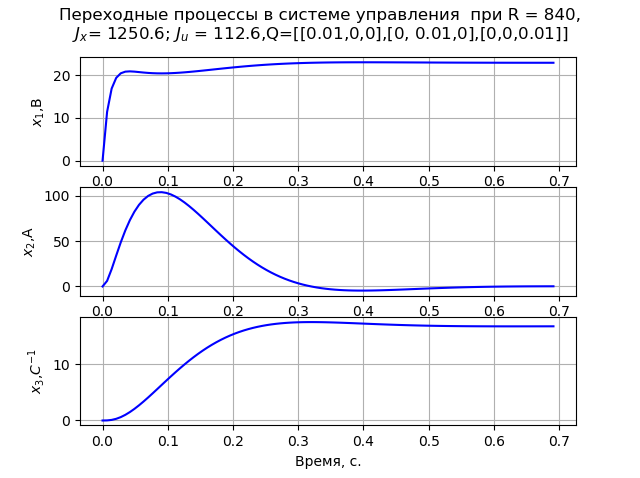

 # -*- coding: utf8 -*- from numpy import* from control.matlab import * from matplotlib import pyplot as plt from scipy.linalg import* def lqr(A,B,Q,R): S =matrix(solve_continuous_are(A, B, Q, R)) K = matrix(inv(R)*(BT*S)) E= eig(AB*K)[0] return K, S, E #   A=matrix([[-100,0,0],[143.678, -16.667,-195.402],[0,1.046,0]]); B=matrix([[2300], [0], [0]]); C=eye(3) D=zeros([3,1]) #    R=[[840]] Q=matrix([[0.01, 0, 0],[0, 0.01, 0],[0, 0, 0.01]]); #  LQR-  [K,S,E]=lqr(A,B,Q,R) #    N=AB*K; NN=NT; w=ss(N,B,C,D) x0=matrix([[220], [147], [162]]); Ct=CT; P1=solve_lyapunov(NN,Ct*Q*C) Kt=KT; x0t=x0.T; Jx=abs((x0t*P1*x0)[0,0]) P2=solve_lyapunov(NN,Kt*R*K); Ju=abs((x0t*P2*x0)[0,0]) fig = plt.figure() plt.suptitle('      R = %s,\n\ $J_{x}$= %s; $J_{u}$ = %s,Q=[[0.01,0,0],[0, 0.01,0],[0,0,0.01]]'%(R[0][0],round(Jx,1),round(Ju,1))) ax1 = fig.add_subplot(311) y,x=step(w[0,0]) ax1.plot(x,y,"b") plt.ylabel('$x_{1}$,B') ax1.grid(True) ax2 = fig.add_subplot(312) y,x=step(w[1,0]) ax2.plot(x,y,"b") plt.ylabel('$x_{2}$,A') ax2.grid(True) ax3 = fig.add_subplot(313) y,x=step(w[2,0]) ax3.plot(x,y,"b") plt.ylabel('$x_{3}$,$C^{-1}$') ax3.grid(True) plt.xlabel(', .') plt.show()

Fig. 2
Mediante la selección adecuada de las matrices R y Q, es posible reducir la corriente de arranque del motor a valores aceptables iguales a (2–2.5) In (Fig. 3). Por ejemplo, con R = 840 y
Q = ([[[0.01,0,0]], [0,0.88,0], [0,0,0.01]], su valor es 292 A, y el tiempo del proceso de transición en estas condiciones es 1.57 s.

Listado del programa (Fig. 3).

 # -*- coding: utf8 -*- from numpy import* from control.matlab import * from matplotlib import pyplot as plt from scipy.linalg import* def lqr(A,B,Q,R): S =matrix(solve_continuous_are(A, B, Q, R)) K = matrix(inv(R)*(BT*S)) E= eig(AB*K)[0] return K, S, E #   A=matrix([[-100,0,0],[143.678, -16.667,-195.402],[0,1.046,0]]); B=matrix([[2300], [0], [0]]); C=eye(3) D=zeros([3,1]) #    R=[[840]] Q=matrix([[0.01,0,0],[0,0.88,0],[0,0,0.01]]); #  LQR-  [K,S,E]=lqr(A,B,Q,R) #    N=AB*K; NN=NT; w=ss(N,B,C,D) x0=matrix([[220], [147], [162]]); Ct=CT; P1=solve_lyapunov(NN,Ct*Q*C) Kt=KT; x0t=x0.T; Jx=abs((x0t*P1*x0)[0,0]) P2=solve_lyapunov(NN,Kt*R*K); Ju=abs((x0t*P2*x0)[0,0]) fig = plt.figure() plt.suptitle('      R = %s,\n\ $J_{x}$= %s; $J_{u}$ = %s,Q=[[0.01,0,0],[0,0.88,0],[0,0,0.01]]'%(R[0][0],round(Jx,1),round(Ju,1))) ax1 = fig.add_subplot(311) y,x=step(w[0,0]) ax1.plot(x,y,"b") plt.ylabel('$x_{1}$,B') ax1.grid(True) ax2 = fig.add_subplot(312) y,x=step(w[1,0]) ax2.plot(x,y,"b") plt.ylabel('$x_{2}$,A') ax2.grid(True) ax3 = fig.add_subplot(313) y,x=step(w[2,0]) ax3.plot(x,y,"b") plt.ylabel('$x_{3}$,$C^{-1}$') ax3.grid(True) plt.xlabel(', .') plt.show()

Fig.3

En todos los casos considerados, las retroalimentaciones de voltaje y corriente son negativas, y en velocidad, positivas, lo que no es deseable de acuerdo con los requisitos de estabilidad. Además, el sistema sintetizado es astático para la tarea y estático para la carga. Por lo tanto, consideramos la síntesis de un controlador PI en el espacio de estado con una variable de estado adicional

x_{4}

$x_ {4}$ - coeficiente de transferencia del integrador.

Representamos la información inicial en forma de matrices:

A = \ begin {bmatrix} & -100 & 0 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 & 0 \\ & 0 & 1.046 & 0 & 0 \\ & 0 & 0 & 1 & 0 \ end {bmatrix}; B = \ begin {bmatrix} 2300 \\ 0 \\ 0 \\ 0 \\\ end {bmatrix}; C = ojo (4)); D = 0

$A = \ begin {bmatrix} & -100 & 0 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 & 0 \\ & 0 & 1.046 & 0 & 0 \\ & 0 & 0 & 1 & 0 \ end {bmatrix}; B = \ begin {bmatrix} 2300 \\ 0 \\ 0 \\ 0 \\\ end {bmatrix}; C = ojo (4)); D = 0$

Los transitorios de tareas correspondientes al criterio MO se obtuvieron en R = 100, q11 = q22 = q33 = 0.001 y q44 = 200. La Figura 4 muestra las variables de estado transitorios que confirman el astatismo del sistema por tarea y por carga.

Listado de programas (Fig. 4).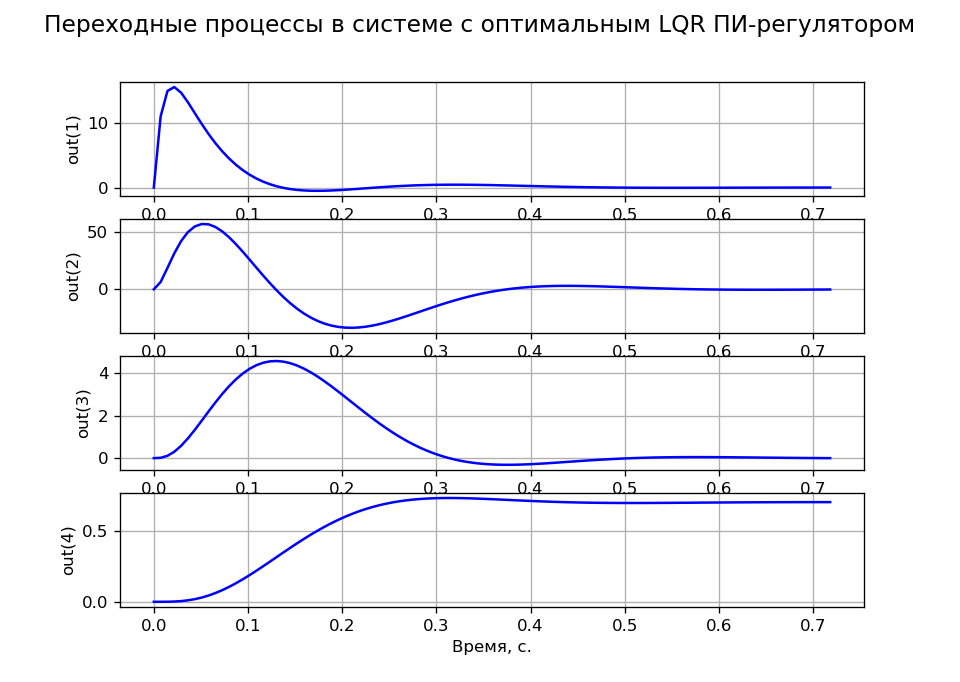

 # -*- coding: utf8 -*- from numpy import* from control.matlab import * from matplotlib import pyplot as plt from scipy.linalg import* def lqr(A,B,Q,R): S =matrix(solve_continuous_are(A, B, Q, R)) K = matrix(inv(R)*(BT*S)) E= eig(AB*K)[0] return K, S, E #   A=matrix([[-100,0,0,0],[143.678, -16.667,-195.402,0],[0,1.046,0,0] ,[0,0,1,0]]); B=matrix([[2300], [0], [0],[0]]); C=matrix([[1, 0, 0,0],[0, 1, 0,0],[0, 0, 1,0],[0, 0, 0,1]]); D=matrix([[0],[0],[0],[0]]); #    R=[[100]]; Q=matrix([[0.001, 0, 0,0],[0, 0.001, 0,0],[0, 0, 0.01,0],[0, 0,0,200]]); #  LQR-  (K,S,E)=lqr(A,B,Q,R) #    N=AB*K; NN=NT; w=ss(N,B,C,D) x0=matrix([[220], [147], [162],[0]]); Ct=CT; P1=solve_lyapunov(NN,Ct*Q*C) Kt=KT; x0t=x0.T; Jx=abs((x0t*P1*x0)[0,0]) P2=solve_lyapunov(NN,Kt*R*K); Ju=abs((x0t*P2*x0)[0,0]) fig = plt.figure(num=None, figsize=(9, 7), dpi=120, facecolor='w', edgecolor='k') plt.suptitle('      LQR -',size=14) ax1 = fig.add_subplot(411) y,x=step(w[0,0]) ax1.plot(x,y,"b") plt.ylabel('out(1)') ax1.grid(True) ax2 = fig.add_subplot(412) y,x=step(w[1,0]) ax2.plot(x,y,"b") plt.ylabel('out(2)') ax2.grid(True) ax3 = fig.add_subplot(413) y,x=step(w[2,0]) ax3.plot(x,y,"b") plt.ylabel('out(3)') ax3.grid(True) ax4 = fig.add_subplot(414) y,x=step(w[3,0]) ax4.plot(x,y,"b") plt.ylabel('out(4)') ax4.grid(True) plt.xlabel(', .') plt.show()

Fig. 4 4
Para determinar la matriz K, la biblioteca de Python Control Systems tiene dos funciones: K = acker (A, B, s) y K = lugar (A, B, s), donde s es el vector, la fila de los polos deseados de la función de transferencia del sistema de control de circuito cerrado. El primer comando solo se puede usar para sistemas con una entrada en u para n≤5. El segundo no tiene tales restricciones, pero la multiplicidad de los polos no debe exceder el rango de la matriz B. Un ejemplo del uso del operador acker () se muestra en la lista y en la (Fig. 5).

Listado de programas (Fig. 5).

 # -*- coding: utf8 -*- from numpy import* from control.matlab import * from matplotlib import pyplot as plt i=(-1)**0.5 A=matrix([[-100,0,0],[143.678, -16.667,-195.402],[0,1.046,0]]); B=matrix([[2300], [0], [0]]); C=eye(3) D=zeros([3,1]) p=[[-9.71+14.97*i -9.71-14.97*i -15.39 -99.72]]; k=acker(A,B,p) H=AB*k; Wss=ss(H,B,C,D); step(Wss) w=tf(Wss) fig = plt.figure() plt.suptitle('   acker()') ax1 = fig.add_subplot(311) y,x=step(w[0,0]) ax1.plot(x,y,"b") ax1.grid(True) ax2 = fig.add_subplot(312) y,x=step(w[1,0]) ax2.plot(x,y,"b") ax2.grid(True) ax3 = fig.add_subplot(313) y,x=step(w[2,0]) ax3.plot(x,y,"b") ax3.grid(True) plt.xlabel(', .') plt.show()

Fig. 5 5

Conclusión

La implementación de la optimización LQR del accionamiento eléctrico que figura en la publicación, teniendo en cuenta el uso de las nuevas funciones lqr () y lyap (), nos permitirá abandonar el uso del programa con licencia MATLAB al estudiar la sección correspondiente de la teoría de control.

Un ejemplo de optimización de LQR en una aeronave (LA)

(un ejemplo es tomado de la publicación de Astrom y Mruray, Capítulo 5 [8] y finalizado por el autor del artículo en términos de reemplazar la función lqr () y reducir la terminología a la generalmente aceptada)

La parte teórica, una breve teoría, la optimización de LQR ya se ha considerado anteriormente, así que pasemos al análisis de código con los comentarios correspondientes:

Bibliotecas necesarias y función de controlador LQR.

 from scipy.linalg import* # scipy   lqr from numpy import * # numpy    from matplotlib.pyplot import * #     from control.matlab import * #  control..ss()  control..step() #     lqr() m = 4; #    . J = 0.0475; #        ***2 #́-       #  . r = 0.25; #     . g = 9.8; #     /**2 c = 0.05; #   () def lqr(A,B,Q,R): X =matrix(solve_continuous_are(A, B, Q, R)) K = matrix(inv(R)*(BT*X)) E= eig(AB*K)[0] return X, K, E

Condiciones iniciales y matrices básicas Modelos A, B, C, D.

 xe = [0, 0, 0, 0, 0, 0];#   x   () ue = [0, m*g]; #   #   A = matrix( [[ 0, 0, 0, 1, 0, 0], [ 0, 0, 0, 0, 1, 0], [ 0, 0, 0, 0, 0, 1], [ 0, 0, (-ue[0]*sin(xe[2]) - ue[1]*cos(xe[2]))/m, -c/m, 0, 0], [ 0, 0, (ue[0]*cos(xe[2]) - ue[1]*sin(xe[2]))/m, 0, -c/m, 0], [ 0, 0, 0, 0, 0, 0 ]]) #   B = matrix( [[0, 0], [0, 0], [0, 0], [cos(xe[2])/m, -sin(xe[2])/m], [sin(xe[2])/m, cos(xe[2])/m], [r/J, 0]]) #   C = matrix([[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0]]) D = matrix([[0, 0], [0, 0]])

Construimos entradas y salidas correspondientes a cambios paso a paso en la posición xy. Los vectores xd e yd corresponden al estado estacionario deseado en el sistema. Las matrices Cx y Cy son las salidas correspondientes del modelo. Para describir la dinámica del sistema, utilizamos un sistema de ecuaciones de matriz de vectores:

\ left \ {\ begin {matrix} xdot = Ax + Bu => xdot = (A-BK) x + xd \\ u = -K (x-xd) \\ y = Cx \\ \ end {matrix} \ right. $

$\ left \ {\ begin {matrix} xdot = Ax + Bu => xdot = (A-BK) x + xd \\ u = -K (x-xd) \\ y = Cx \\ \ end {matrix} \ right. $$

La dinámica de un bucle cerrado se puede modelar utilizando la función step (), para K \ cdot xd y K \ cdot xd como vectores de entrada, donde:

 xd = matrix([[1], [0], [0], [0], [0], [0]]); yd = matrix([[0], [1], [0], [0], [0], [0]]);

La biblioteca de control actual 0.8.1 solo admite parte de las funciones de SISO Matlab para crear controladores de retroalimentación, por lo tanto, para leer datos del controlador, es necesario crear vectores de índice lat (), alt () para dinámica lateral -x y vertical -y.

 lat = (0,2,3,5); alt = (1,4); #    Ax = (A[lat, :])[:, lat]; Bx = B[lat, 0]; Cx = C[0, lat]; Dx = D[0, 0]; Ay = (A[alt, :])[:, alt]; By = B[alt, 1]; Cy = C[1, alt]; Dy = D[1, 1]; #      K Qx1 = diag([1, 1, 1, 1, 1, 1]); Qu1a = diag([1, 1]); X,K,E =lqr(A, B, Qx1, Qu1a) K1a = matrix(K); #      x H1ax = ss(Ax - Bx*K1a[0,lat], Bx*K1a[0,lat]*xd[lat,:], Cx, Dx); (Yx, Tx) = step(H1ax, T=linspace(0,10,100)); #     y H1ay = ss(Ay - By*K1a[1,alt], By*K1a[1,alt]*yd[alt,:], Cy, Dy); (Yy, Ty) = step(H1ay, T=linspace(0,10,100));

Los gráficos se muestran secuencialmente, uno para cada tarea.

 figure(); title("   x  y") plot(Tx.T, Yx.T, '-', Ty.T, Yy.T, '--'); plot([0, 10], [1, 1], 'k-'); axis([0, 10, -0.1, 1.4]); ylabel(' '); xlabel(''); legend(('x', 'y'), loc='lower right'); grid() show()

Tabla: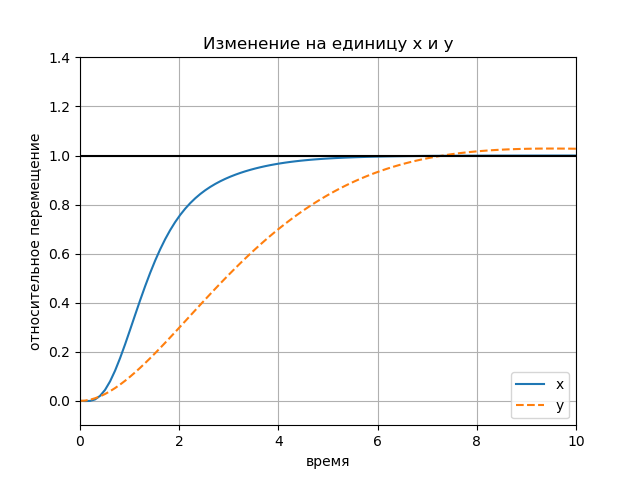

La influencia de la amplitud de las acciones de entrada.

 #     Qu1a = diag([1, 1]); X,K,E =lqr(A, B, Qx1, Qu1a) K1a = matrix(K); H1ax = ss(Ax - Bx*K1a[0,lat], Bx*K1a[0,lat]*xd[lat,:], Cx, Dx); Qu1b = (40**2)*diag([1, 1]); X,K,E =lqr(A, B, Qx1, Qu1b) K1b = matrix(K); H1bx = ss(Ax - Bx*K1b[0,lat], Bx*K1b[0,lat]*xd[lat,:],Cx, Dx); Qu1c = (200**2)*diag([1, 1]); X,K,E =lqr(A, B, Qx1, Qu1c) K1c = matrix(K); H1cx = ss(Ax - Bx*K1c[0,lat], Bx*K1c[0,lat]*xd[lat,:],Cx, Dx); figure(); [Y1, T1] = step(H1ax, T=linspace(0,10,100)); [Y2, T2] = step(H1bx, T=linspace(0,10,100)); [Y3, T3] = step(H1cx, T=linspace(0,10,100)); plot(T1.T, Y1.T, 'r-'); plot(T2.T, Y2.T, 'b-'); plot(T3.T, Y3.T, 'g-'); plot([0 ,10], [1, 1], 'k-'); axis([0, 10, -0.1, 1.4]); title("   ") legend(('1', '$1,6\cdot 10^{3}$','$4\cdot 10^{4}$'), loc='lower right'); text(5.3, 0.4, 'rho'); ylabel(' '); xlabel(''); grid() show()

Tabla:

Respuesta transitoria

 #  Qx    Qx2 = CT * C; Qu2 = 0.1 * diag([1, 1]); X,K,E =lqr(A, B, Qx2, Qu2) K2 = matrix(K); H2x = ss(Ax - Bx*K2[0,lat], Bx*K2[0,lat]*xd[lat,:], Cx, Dx); H2y = ss(Ay - By*K2[1,alt], By*K2[1,alt]*yd[alt,:], Cy, Dy); figure(); [Y2x, T2x] = step(H2x, T=linspace(0,10,100)); [Y2y, T2y] = step(H2y, T=linspace(0,10,100)); plot(T2x.T, Y2x.T, T2y.T, Y2y.T) plot([0, 10], [1, 1], 'k-'); axis([0, 10, -0.1, 1.4]); title(" ") ylabel(' '); xlabel(''); legend(('x', 'y'), loc='lower right'); grid() show()

Tabla: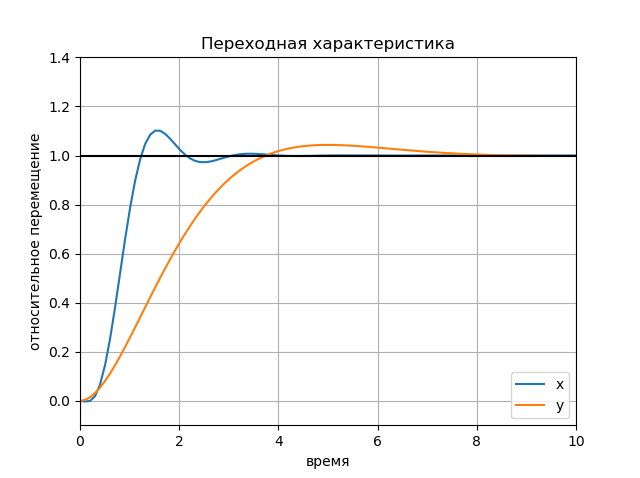

Respuesta transitoria basada en la física

 #    #       #   1 .     10 . Qx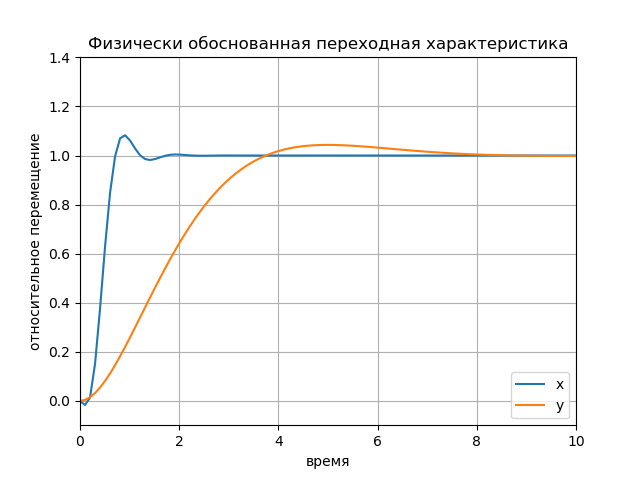3 = diag([100, 10, 2*pi/5, 0, 0, 0]); Qu3 = 0.1 * diag([1, 10]); X,K,E =lqr(A, B, Qx3, Qu3) K3 = matrix(K); H3x = ss(Ax - Bx*K3[0,lat], Bx*K3[0,lat]*xd[lat,:], Cx, Dx); H3y = ss(Ay - By*K3[1,alt], By*K3[1,alt]*yd[alt,:], Cy, Dy); figure(); [Y3x, T3x] = step(H3x, T=linspace(0,10,100)); [Y3y, T3y] = step(H3y, T=linspace(0,10,100)); plot(T3x.T, Y3x.T, T3y.T, Y3y.T) axis([0, 10, -0.1, 1.4]); title("   ") ylabel(' '); xlabel(''); legend(('x', 'y'), loc='lower right'); grid() show()

Tabla:

Conclusión

La implementación de la optimización LQR en la aeronave presentada en la publicación, teniendo en cuenta el uso de la nueva función lqr (), nos permitirá abandonar el uso del programa licenciado MATLAB al estudiar la sección correspondiente de la teoría de control.

Referencias

1. Matemáticas en los dedos: controlador lineal-cuadrático.

2. El espacio de estado en los problemas de diseño de sistemas de control óptimos.

3. Uso de la biblioteca de sistemas de control de Python para diseñar sistemas de control automático.

4. Biblioteca de sistemas de control de Python.

5. Python: no se puede importar el módulo slycot en spyder (RuntimeError & ImportError).

6. Biblioteca de sistemas de control de Python.

7. Criterios para un control óptimo y optimización de lqr en un accionamiento eléctrico.

Optimización del sistema de control LQR

Introduccion

Sustanciación matemática del método de optimización dinámica.

Características de la implementación del método de optimización dinámica usando Python

Un ejemplo de optimización de LQR en un accionamiento eléctrico

Conclusión

Un ejemplo de optimización de LQR en una aeronave (LA)

Conclusión

Referencias

More articles: