Cómo un rompecabezas para niños ayuda a revelar los secretos del magnetismo

Los imanes han sido familiares para las personas desde la antigüedad, pero la física del ferromagnetismo sigue siendo un misterio. Ahora un rompecabezas familiar acerca a los físicos a responder preguntas

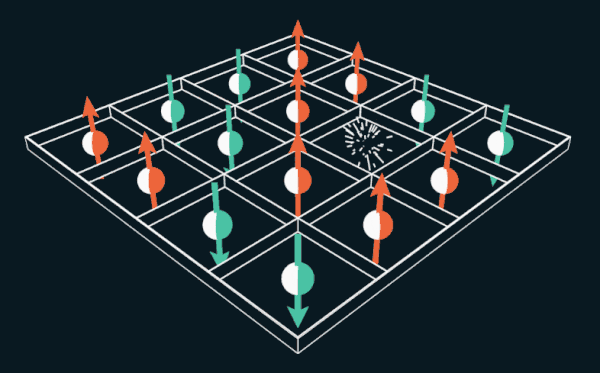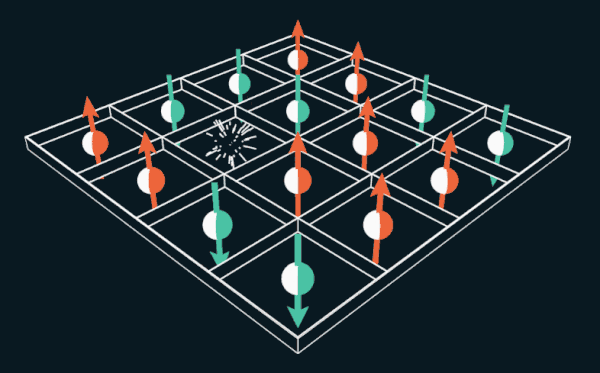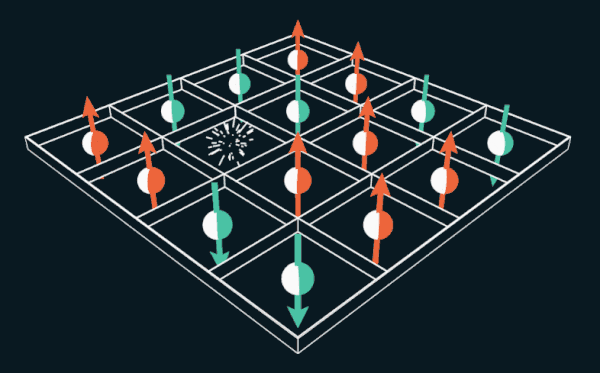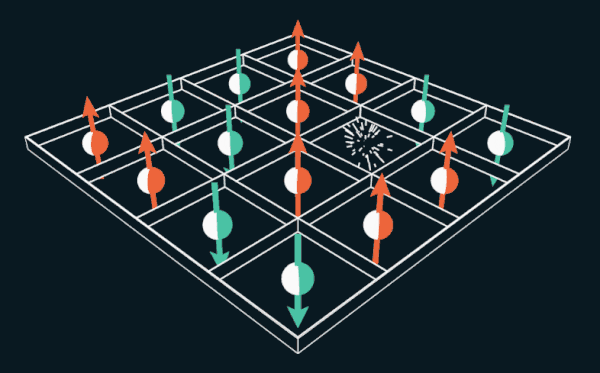El juego de 15 ofrece al jugador mover las fichas numeradas dentro de la cuadrícula. Si reemplaza los números con los giros de electrones, el rompecabezas se puede usar para explicar cómo funcionan los imanes permanentes.

Durante varios meses en el año 1880, regiones enteras de los Estados Unidos sucumbieron a la adicción, análogos de los cuales nadie había visto previamente. "Una epidemia ha estallado literalmente en todo el país", escribió la revista The Weekly News-Democrat en Imperia, Kansas, el 12 de marzo de 1880. "Ciudades enteras son atraídas, la gente pierde el sueño y se vuelve loca". La epidemia se extendió a Europa e incluso llegó a Australia con Nueva Zelanda.

La enfermedad se ha convertido en una nueva pasión: desalentar el simple rompecabezas mecánico "15". Todavía se conoce, y consiste en un campo cuadrado de 4x4 en el que puede mover 15 fichas numeradas para organizarlas en orden.

Según los estándares actuales, el juego parece pasado de moda, pero en 1880 estaba en la cima de la popularidad. "Ningún niño puede resistir tal entretenimiento, ningún adulto será tan fuerte o arrogante para escapar de su encanto", escribió el periódico. Y la decepción puede haber surgido del hecho matemáticamente comprobado de que solo la mitad de las configuraciones de este rompecabezas pueden resolverse con éxito (lo que probablemente era desconocido para quienes quedaron bajo su influencia).

Hoy, casi 140 años después, el interés en el juego "15" ha revivido nuevamente, pero esta vez no actúa como una distracción, sino como una forma de entender un rompecabezas aparentemente no relacionado y mucho más complicado: cómo funcionan los imanes.

Los imanes permanentes, como los que cuelgan de la puerta de su refrigerador, son atraídos por un fenómeno como el ferromagnetismo . En un ferromagnet, los espines de los electrones están alineados y juntos generan un campo magnético. Más precisamente, los metales como el hierro, el cobalto y el níquel exhiben magnetismo de banda, ya que sus electrones pueden moverse libremente dentro del material. Cada electrón tiene su propio momento magnético, pero para comprender cómo y por qué todos estos momentos se alinean en un imán, es necesario calcular las interacciones cuánticas entre todos los electrones, lo cual es excesivamente difícil de hacer.

"El magnetismo de zona es en realidad uno de los mayores desafíos en la física teórica de la materia condensada", dijo Wai Lee, físico de la Universidad Johns Hopkins.

Sin embargo, Lee y dos estudiantes de posgrado, Eric Bobrov y Keaton Stewbis, pueden haber estado un poco más cerca de resolver este problema. Usando el acertijo matemático "15", expandieron el conocido teorema que describe el estado idealizado del magnetismo de zona. En su nuevo análisis , publicado en Physical Review B, extienden el teorema para explicar un sistema más amplio y realista, que podría conducir a un modelo de imanes más preciso.

"Es un gran trabajo", dijo Daniel Arovas , físico de la Universidad de California en San Diego. "Me gusta especialmente este trabajo debido al hecho de que hay muy pocos resultados detallados con respecto al magnetismo de zona y están demasiado fragmentados".

Agujero saltando

En el nivel más básico, los electrones en un metal deben obedecer dos restricciones principales. En primer lugar, todos están cargados negativamente, por lo tanto, se repelen entre sí. En segundo lugar, los electrones deben obedecer a los llamados El principio de Pauli, que postula que dos partículas [con un giro de medio entero / aprox. trans.] no puede estar en el mismo estado cuántico. Esto significa que los electrones con el mismo espín, proporcional al momento magnético de un electrón, no pueden ocupar el mismo estado en un átomo de metal. Y dos electrones con giros opuestos pueden.

Resulta que la forma más simple de satisfacer tanto la repulsión mutua como las limitaciones del principio de Pauli para un grupo de electrones será separando y alineando los espines, como resultado de lo cual el material se vuelve ferromagnético.

Sin embargo, esta es solo una imagen simplificada. Los físicos no pudieron construir un modelo detallado de la apariencia de un patrón tan organizado de giros alineados a partir de innumerables interacciones cuánticas entre electrones individuales. Por ejemplo, como explicó Lee, la función de onda de un electrón, una descripción matemática compleja de sus propiedades cuánticas, puede confundirse con la función de onda de otro electrón. Para comprender a fondo cómo el comportamiento de las partículas individuales conduce a la aparición de un fenómeno colectivo como el ferromagnetismo, tendrá que controlar la función de onda de cada electrón en el sistema, mientras cambia continuamente la función de onda de cada uno de los electrones restantes en el proceso de su interacción. En la práctica, este enredo generalizado hace imposible escribir las ecuaciones completas y completas necesarias para describir el ferromagnetismo.

En cambio, los físicos, incluido Lee, están tratando de recopilar información mediante el estudio de modelos simplificados e idealizados que describen la física detrás del ferromagnetismo. En particular, su último trabajo extiende un importante descubrimiento realizado hace más de 50 años.

A mediados de la década de 1960, dos físicos de lados opuestos del mundo obtuvieron de forma independiente evidencia que demostraba por qué los electrones deberían alinearse y crear un estado ferromagnético. David Tules, entonces físico que trabajó en la Universidad de Cambridge y finalmente ganó el Premio Nobel 2016, y Yosuke Nagaoka, físico en la Universidad de Nagoya que estaba visitando la Universidad de California en San Diego en ese momento, publicaron sus pruebas en 1965 y 1966, respectivamente. . Su resultado, llamado teorema de Nagaoki-Tules (o simplemente el teorema de Nagaoki), se basa en un sistema idealizado de electrones ubicados en una red atómica. Entonces, aunque no explica el comportamiento de los imanes reales, todavía era importante, mostrando por primera vez en principio por qué los espines de electrones deberían estar alineados. Y dado que su análisis era evidencia matemática, eran precisos, no cargados de aproximaciones típicas de la física.

Para comprender el teorema, imagine un enrejado cuadrado bidimensional. Cada nodo puede colocar dos electrones con espines opuestos, pero el teorema sugiere que colocar dos electrones en un lugar requerirá una cantidad infinita de energía. Esto asegura que solo habrá un electrón en cada lugar. En esta configuración, cada electrón puede dirigir su giro hacia arriba o hacia abajo. No tienen que alinearse, por lo que dicho sistema no debería ser un ferromagnet.


Wai Lee, físico en la Universidad Johns Hopkins

Ahora eliminamos un electrón. Como resultado, habrá un lugar vacante llamado hoyo. Un electrón vecino puede deslizarse en un agujero, dejando un nuevo espacio vacío. Otro electrón puede moverse a un nuevo lugar vacío, dejando otro agujero atrás. En este ejemplo, un agujero, de hecho, salta de un lugar a otro, moviéndose alrededor de la cuadrícula. Thules y Nagaoka descubrieron que en este caso, cuando se agrega un solo agujero, los electrones se alinearán espontáneamente. Probaron que sería el estado con menos energía, el estado de un ferromagnet.

Arovas explica que para que un sistema entre en un estado con la energía más baja, un agujero debe poder moverse libremente sin alterar la configuración de los espines de electrones; tal proceso requerirá energía adicional. Pero cuando un agujero se mueve, los electrones también deben moverse. Para que los electrones se muevan sin alterar la configuración de los espines, deben estar alineados.

"El teorema de Nagaoka es uno de los pocos ejemplos que pueden probar matemáticamente casos individuales de ferromagnetismo", dijo Masaki Oshikawa , físico de la Universidad de Tokio. "Pero desde el punto de vista de la física, todo esto es muy artificial".

Por ejemplo, los electrones requieren mucha energía para superar su repulsión mutua y establecerse en un lugar, pero no infinito, como lo requiere el teorema. Además, la imagen dibujada por Nagaoka y Tules se aplica solo a celosías simples: celosías bidimensionales que consisten en cuadrados o triángulos, o celosías cúbicas tridimensionales. En la naturaleza, el ferromagnetismo surge en muchos metales con estructuras de todo tipo.

Si el teorema de Nagaoka-Tules realmente explica el ferromagnetismo, entonces debería ser aplicable a todas las redes. La gente asumió que sí, dijo Lee. "Pero nadie dio pruebas reales y claras". Bueno, eso es, todavía.

Azulejos con respaldo

En 1989, Hal Tasaki, físico de la Universidad Gakushuin de Japón, amplió este teorema para descubrir que sería aplicable siempre que la red tuviera una propiedad matemática como la conectividad. Tome el caso simple de una red cuadrada con un agujero en movimiento. Si, al mover un agujero, puede reproducir cualquier configuración de giros, manteniendo el número de electrones, con giros dirigidos hacia arriba y hacia abajo, entonces se cumple la condición de conexión.

Pero aparte de las redes cuadradas y triangulares, y los cubos tridimensionales, no estaba claro si la condición conectada se cumpliría en otros casos y, por lo tanto, qué tan ampliamente podría aplicarse este teorema.

Para lidiar con este problema, Lee comenzó con una cuadrícula hexagonal de panal. Sus alumnos, Bobrov y Stubis, trabajando en esta tarea, se dieron cuenta de que se asemeja a una manía del siglo XIX: el rompecabezas "15". Cambie las etiquetas de los azulejos de los números a la parte posterior, hacia arriba y hacia abajo, y el rompecabezas se vuelve equivalente al ferromagnet de Nagaoki, con un agujero que se mueve a lo largo de la red de electrones.

El rompecabezas se permite cuando tiene la oportunidad de redistribuir los mosaicos en cualquier secuencia, lo que coincide completamente con la condición de conectividad. Entonces, la cuestión de si la condición de conectividad se satisface para una red determinada se convierte en la cuestión de si es posible resolver un rompecabezas equivalente en una red de dicha estructura.

Resulta que en 1974 el matemático Richard Wilson, que ahora trabaja en el Instituto de Tecnología de California, resolvió este problema resumiendo y resolviendo el rompecabezas "15" para todas las cuadrículas. Como parte de la prueba, demostró que en casi todas las redes inseparables (en las que todos los nodos permanecen conectados incluso después de eliminar uno de ellos), puede mover las fichas y obtener cualquier configuración, siempre y cuando el número de movimientos permanezca uniforme. La única excepción es que los polígonos individuales son más grandes que un triángulo, y algo llamado "gráfico θnulo", en el cual el vértice en el centro del hexágono está conectado a dos vértices opuestos.

Los investigadores pudieron aplicar directamente la prueba de Wilson al teorema de Nagaoka-Tules. Probaron que la condición de conectividad se cumple para un sistema de electrones y un solo orificio en casi todas las redes, incluidas las estructuras comunes como los panales bidimensionales y las redes tridimensionales en forma de diamante. Dos excepciones, polígonos más grandes que un triángulo, y el gráfico θ cero, en cualquier caso, no ocurren en ferromagnetos reales.

Explosión del agujero

Usar el rompecabezas "15" es un enfoque nuevo y potencialmente fructífero, dijo Sriram Shastri , físico de la Universidad de California en Santa Cruz. "Me gusta el hecho de que trajo al trabajo un nuevo lenguaje, un nuevo conjunto de conexiones con la teoría de grafos", dijo. "Creo que esta es una conexión rica, en el futuro puede convertirse en una rica fuente de ideas". Pero, aunque la investigación está dando un importante paso adelante, los problemas persisten.

Una complicación es que el teorema de Nagaoki-Tules no siempre funciona cuando un agujero en movimiento necesita dar un número impar de pasos mientras se mueve a lo largo de la red, dijo Shastri. Quizás el problema más sorprendente es que el teorema requiere la presencia de exactamente un agujero, ni más ni menos. Sin embargo, los metales están llenos de agujeros; a menudo ocupan hasta la mitad de la red.

Pero los físicos intentaron generalizar el teorema de los sistemas con muchos agujeros. Utilizando métodos numéricos, los físicos han demostrado que el ferromagnetismo de Nagaoki parece funcionar para una red cuadrada de tamaño finito, hasta el 30% de los cuales son agujeros. En el trabajo actual, los investigadores aplicaron técnicas analíticas precisas a los panales bidimensionales y a las redes tridimensionales en forma de diamante. El ferromagnetismo de Nagaoki, aparentemente, existe siempre y cuando el número de agujeros no exceda el número de nodos de la red en el grado 1/2 para las células, y en el grado 2/5 para la red en forma de diamante.

Estas soluciones exactas pueden conducir a un modelo más completo de magnetismo de zona. "Este es solo un pequeño paso para establecer un riguroso punto de partida matemático para futuras investigaciones", dijo Lee.