Ecuaciones diferenciales ordinarias neurales

Una proporción significativa de procesos se describe mediante ecuaciones diferenciales, esta puede ser la evolución del sistema físico a lo largo del tiempo, la condición médica del paciente, las características fundamentales del mercado de valores, etc. Los datos sobre tales procesos son consistentes y de naturaleza continua, en el sentido de que las observaciones son simplemente manifestaciones de algún tipo de estado continuamente cambiante.

También hay otro tipo de datos en serie, son datos discretos, por ejemplo, datos de tareas de PNL. El estado en dichos datos varía discretamente: de un carácter o palabra a otro.

Ahora, ambos tipos de datos en serie suelen ser procesados por redes recursivas, aunque son de naturaleza diferente y parecen requerir enfoques diferentes.

Se presentó un artículo muy interesante en la última conferencia de NIPS , que puede ayudar a resolver este problema. Los autores proponen un enfoque que llamaron EDO neuronales .

Aquí intenté reproducir y resumir los resultados de este artículo para familiarizarme un poco con su idea. Me parece que esta nueva arquitectura puede encontrar un lugar en las herramientas estándar de un científico de datos junto con redes convolucionales y recurrentes.

Figura 1: La propagación inversa en gradiente continuo requiere resolver la ecuación diferencial aumentada en el tiempo.

Las flechas representan el ajuste de gradientes propagados hacia atrás por gradientes de las observaciones.

Ilustración del artículo original.

Planteamiento del problema

Que haya un proceso que obedezca a alguna EDO desconocida y que haya varias observaciones (ruidosas) a lo largo de la trayectoria del proceso

$\ frac {dz} {dt} = f (z (t), t) \; (1)$

$\ {(z_0, t_0), (z_1, t_1), ..., (z_M, t_M) \} - \ text {observaciones}$

Cómo encontrar una aproximación $\ widehat {f} (z, t, \ theta)$ funciones de altavoz f (z, t)

?

Primero, considere una tarea más simple: solo hay 2 observaciones, al principio y al final de la trayectoria, (z_0, t_0), (z_1, t_1)

.

La evolución del sistema comienza desde el estado z_0, t_0

a tiempo

con alguna función dinámica parametrizada utilizando cualquier método de evolución de sistemas ODE. Después de que el sistema esté en un nuevo estado $\ hat {z_1}, t_1$ , se compara con el estado z_1

y la diferencia entre ellos se minimiza variando los parámetros $\ theta$ Funciones dinámicas.

O, más formalmente, considere minimizar la función de pérdida $L (\ hat {z_1})$ :

$L (z (t_1)) = L \ Big (\ int_ {t_0} ^ {t_1} f (z (t), t, \ theta) dt \ Big) = L \ big (\ text {ODESolve} (z ( t_0), f, t_0, t_1, \ theta) \ big) \; (2)$

Para minimizar

, necesita calcular los gradientes para todos sus parámetros: $z (t_0), t_0, t_1, \ theta$ . Para hacer esto, primero debe determinar cómo

depende del estado en cada momento (z (t))

$a (t) = - \ frac {\ partial L} {\ partial z (t)} \; (3)$

se llama estado adjunto , su dinámica viene dada por otra ecuación diferencial, que puede considerarse un análogo continuo de diferenciación de una función compleja ( regla de cadena ):

$\ frac {d a (t)} {d t} = -a (t) \ frac {\ partial f (z (t), t, \ theta)} {\ partial z} \; (4)$

El resultado de esta fórmula se puede encontrar en el apéndice del artículo original.

Los vectores en este artículo deben considerarse vectores en minúsculas, aunque el artículo original usa tanto una representación de fila como de columna.

Al resolver diffur (4) en el tiempo, obtenemos una dependencia del estado inicial z (t_0)

$\ frac {\ partial L} {\ partial z (t_0)} = \ int_ {t_1} ^ {t_0} a (t) \ frac {\ partial f (z (t), t, \ theta)} {\ partial z} dt \; (5)$

Para calcular el gradiente con respecto a

y $\ theta$ , simplemente puede considerarlos parte del estado. Esta condición se llama aumentada . La dinámica de este estado se obtiene trivialmente de la dinámica original:

$\ frac {d} {dt} \ begin {bmatrix} z \\ \ theta \\ t \ end {bmatrix} (t) = f _ {\ text {aug}} ([z, \ theta, t]): = \ begin {bmatrix} f ([z, \ theta, t]) \\ 0 \\ 1 \ end {bmatrix} \; (6)$

Entonces el estado conjugado a este estado aumentado:

$a _ {\ text {aug}}: = \ begin {bmatrix} a \\ a _ {\ theta} \\ a_t \ end {bmatrix}, a _ {\ theta} (t): = \ frac {\ partial L} { \ partial \ theta (t)}, a_t (t): = \ frac {\ partial L} {\ partial t (t)} \; (7)$

Dinámica Aumentada Gradiente:

$\ frac {\ partial f _ {\ text {aug}}} {\ partial [z, \ theta, t]} = \ begin {bmatrix} \ frac {\ partial f} {\ partial z} &; \ frac {\ partial f} {\ partial \ theta} &; \ frac {\ partial f} {\ partial t} \\ 0 &; 0 &; 0 \\ 0 &; 0 &; 0 \ end {bmatrix} \; (8)$

La ecuación diferencial del estado aumentado conjugado de la fórmula (4) entonces:

$\ frac {d a _ {\ text {aug}}} {dt} = - \ begin {bmatrix} a \ frac {\ partial f} {\ partial z} &; a \ frac {\ partial f} {\ partial \ theta} &; a \ frac {\ partial f} {\ partial t} \ end {bmatrix} \; (9)$

Resolver esta ODE en el tiempo produce:

$\ frac {\ partial L} {\ partial z (t_0)} = \ int_ {t_1} ^ {t_0} a (t) \ frac {\ partial f (z (t), t, \ theta)} {\ partial z} dt \; (10)$

$\ frac {\ partial L} {\ partial \ theta} = \ int_ {t_1} ^ {t_0} a (t) \ frac {\ partial f (z (t), t, \ theta)} {\ partial \ theta } dt \; (11)$

$\ frac {\ partial L} {\ partial t_0} = \ int_ {t_1} ^ {t_0} a (t) \ frac {\ partial f (z (t), t, \ theta)} {\ partial t} dt \; (12)$

Que pasa con

$\ frac {\ partial L} {\ partial t_1} = - a (t) \ frac {\ partial f (z (t), t, \ theta)} {\ partial t} \; (13)$

da gradientes en todos los parámetros de entrada al solucionador ODESolve ODE.

Todos los gradientes (10), (11), (12), (13) se pueden calcular juntos en una llamada ODESolve con la dinámica del estado aumentado conjugado (9).

Ilustración del artículo original.

El algoritmo anterior describe la propagación inversa del gradiente de la solución ODE para observaciones sucesivas.

En el caso de varias observaciones en una trayectoria, todo se calcula de la misma manera, pero en los momentos de observaciones, el inverso del gradiente distribuido debe ajustarse con gradientes de la observación actual, como se muestra en la Figura 1 .

Implementación

El siguiente código es mi implementación de EDO neuronales . Lo hice simplemente para comprender mejor lo que está sucediendo. Sin embargo, está muy cerca de lo que se implementa en el repositorio de los autores del artículo. Contiene todo el código que necesita comprender en un solo lugar, también está un poco más comentado. Para aplicaciones y experimentos reales, aún es mejor utilizar la implementación de los autores del artículo original.

import math import numpy as np from IPython.display import clear_output from tqdm import tqdm_notebook as tqdm import matplotlib as mpl import matplotlib.pyplot as plt %matplotlib inline import seaborn as sns sns.color_palette("bright") import matplotlib as mpl import matplotlib.cm as cm import torch from torch import Tensor from torch import nn from torch.nn import functional as F from torch.autograd import Variable use_cuda = torch.cuda.is_available()

Primero debe implementar cualquier método para la evolución de los sistemas ODE. Para simplificar, el método de Euler se implementa aquí, aunque cualquier método explícito o implícito es adecuado.

 def ode_solve(z0, t0, t1, f): """     -   """ h_max = 0.05 n_steps = math.ceil((abs(t1 - t0)/h_max).max().item()) h = (t1 - t0)/n_steps t = t0 z = z0 for i_step in range(n_steps): z = z + h * f(z, t) t = t + h return z

También describe la superclase de una función dinámica parametrizada con un par de métodos útiles.

Primero: debe devolver todos los parámetros de los que depende la función en forma de vector.

En segundo lugar: es necesario calcular la dinámica aumentada. Esta dinámica depende del gradiente de la función parametrizada en términos de parámetros y datos de entrada. Para no tener que registrar el gradiente con cada mano para cada nueva arquitectura, utilizaremos el método torch.autograd.grad .

 class ODEF(nn.Module): def forward_with_grad(self, z, t, grad_outputs): """Compute f and a df/dz, a df/dp, a df/dt""" batch_size = z.shape[0] out = self.forward(z, t) a = grad_outputs adfdz, adfdt, *adfdp = torch.autograd.grad( (out,), (z, t) + tuple(self.parameters()), grad_outputs=(a), allow_unused=True, retain_graph=True ) #  grad       , #  expand   if adfdp is not None: adfdp = torch.cat([p_grad.flatten() for p_grad in adfdp]).unsqueeze(0) adfdp = adfdp.expand(batch_size, -1) / batch_size if adfdt is not None: adfdt = adfdt.expand(batch_size, 1) / batch_size return out, adfdz, adfdt, adfdp def flatten_parameters(self): p_shapes = [] flat_parameters = [] for p in self.parameters(): p_shapes.append(p.size()) flat_parameters.append(p.flatten()) return torch.cat(flat_parameters)

El siguiente código describe la propagación hacia adelante y hacia atrás para las EDO neuronales . Es necesario separar este código del módulo torch.nn.Module principal en forma de la función torch.autograd.Function porque en este último puede implementar un método de propagación inversa arbitrario, en lugar de un módulo. Entonces esto es solo una muleta.

Esta característica subyace a todo el enfoque Neural ODE .

 class ODEAdjoint(torch.autograd.Function): @staticmethod def forward(ctx, z0, t, flat_parameters, func): assert isinstance(func, ODEF) bs, *z_shape = z0.size() time_len = t.size(0) with torch.no_grad(): z = torch.zeros(time_len, bs, *z_shape).to(z0) z[0] = z0 for i_t in range(time_len - 1): z0 = ode_solve(z0, t[i_t], t[i_t+1], func) z[i_t+1] = z0 ctx.func = func ctx.save_for_backward(t, z.clone(), flat_parameters) return z @staticmethod def backward(ctx, dLdz): """ dLdz shape: time_len, batch_size, *z_shape """ func = ctx.func t, z, flat_parameters = ctx.saved_tensors time_len, bs, *z_shape = z.size() n_dim = np.prod(z_shape) n_params = flat_parameters.size(0) #   , #       def augmented_dynamics(aug_z_i, t_i): """   -     t_i -   : bs, 1 aug_z_i -   : bs, n_dim*2 + n_params + 1 """ #     z_i, a = aug_z_i[:, :n_dim], aug_z_i[:, n_dim:2*n_dim] # Unflatten z and a z_i = z_i.view(bs, *z_shape) a = a.view(bs, *z_shape) with torch.set_grad_enabled(True): t_i = t_i.detach().requires_grad_(True) z_i = z_i.detach().requires_grad_(True) faug = func.forward_with_grad(z_i, t_i, grad_outputs=a) func_eval, adfdz, adfdt, adfdp = faug adfdz = adfdz if adfdz is not None else torch.zeros(bs, *z_shape) adfdp = adfdp if adfdp is not None else torch.zeros(bs, n_params) adfdt = adfdt if adfdt is not None else torch.zeros(bs, 1) adfdz = adfdz.to(z_i) adfdp = adfdp.to(z_i) adfdt = adfdt.to(z_i) # Flatten f and adfdz func_eval = func_eval.view(bs, n_dim) adfdz = adfdz.view(bs, n_dim) return torch.cat((func_eval, -adfdz, -adfdp, -adfdt), dim=1) dLdz = dLdz.view(time_len, bs, n_dim) # flatten dLdz   with torch.no_grad(): ##      #    , #       adj_z = torch.zeros(bs, n_dim).to(dLdz) adj_p = torch.zeros(bs, n_params).to(dLdz) #    z  p,        adj_t = torch.zeros(time_len, bs, 1).to(dLdz) for i_t in range(time_len-1, 0, -1): z_i = z[i_t] t_i = t[i_t] f_i = func(z_i, t_i).view(bs, n_dim) #      dLdz_i = dLdz[i_t] dLdt_i = torch.bmm(torch.transpose(dLdz_i.unsqueeze(-1), 1, 2), f_i.unsqueeze(-1))[:, 0] #     adj_z += dLdz_i adj_t[i_t] = adj_t[i_t] - dLdt_i #      aug_z = torch.cat(( z_i.view(bs, n_dim), adj_z, torch.zeros(bs, n_params).to(z) adj_t[i_t]), dim=-1 ) #  ()      aug_ans = ode_solve(aug_z, t_i, t[i_t-1], augmented_dynamics) #       adj_z[:] = aug_ans[:, n_dim:2*n_dim] adj_p[:] += aug_ans[:, 2*n_dim:2*n_dim + n_params] adj_t[i_t-1] = aug_ans[:, 2*n_dim + n_params:] del aug_z, aug_ans ##         #    dLdz_0 = dLdz[0] dLdt_0 = torch.bmm(torch.transpose(dLdz_0.unsqueeze(-1), 1, 2), f_i.unsqueeze(-1))[:, 0] #  adj_z += dLdz_0 adj_t[0] = adj_t[0] - dLdt_0 return adj_z.view(bs, *z_shape), adj_t, adj_p, None

Ahora, para su comodidad, ajuste esta función en nn.Module .

 class NeuralODE(nn.Module): def __init__(self, func): super(NeuralODE, self).__init__() assert isinstance(func, ODEF) self.func = func def forward(self, z0, t=Tensor([0., 1.]), return_whole_sequence=False): t = t.to(z0) z = ODEAdjoint.apply(z0, t, self.func.flatten_parameters(), self.func) if return_whole_sequence: return z else: return z[-1]

Solicitud

Recuperación de la función dinámica real (verificación de aproximación)

Como prueba básica, verifiquemos ahora si Neural ODE puede restaurar la verdadera función de la dinámica utilizando datos de observación.

Para hacer esto, primero determinamos la función dinámica del ODE, evolucionamos la trayectoria en función de ella y luego intentamos restaurarla desde la función dinámica parametrizada al azar.

Primero, verifiquemos el caso más simple de una EDO lineal. La función dinámica es solo la acción de una matriz.

$\ frac {dz} {dt} = \ begin {bmatrix} -0.1 &; -1.0 \\ 1.0 &; -0.1 \ end {bmatrix} z$

La función entrenada se parametriza mediante una matriz aleatoria.

Además, una dinámica un poco más sofisticada (sin un gif, porque el proceso de aprendizaje no es tan hermoso :))
La función de aprendizaje aquí es una red totalmente conectada con una capa oculta.

Código

 class LinearODEF(ODEF): def __init__(self, W): super(LinearODEF, self).__init__() self.lin = nn.Linear(2, 2, bias=False) self.lin.weight = nn.Parameter(W) def forward(self, x, t): return self.lin(x)

La función dinámica es solo una matriz

 class SpiralFunctionExample(LinearODEF): def __init__(self): matrix = Tensor([[-0.1, -1.], [1., -0.1]]) super(SpiralFunctionExample, self).__init__(matrix)

Matriz parametrizada al azar

 class RandomLinearODEF(LinearODEF): def __init__(self): super(RandomLinearODEF, self).__init__(torch.randn(2, 2)/2.)

Dinámica para trayectorias más sofisticadas.

 class TestODEF(ODEF): def __init__(self, A, B, x0): super(TestODEF, self).__init__() self.A = nn.Linear(2, 2, bias=False) self.A.weight = nn.Parameter(A) self.B = nn.Linear(2, 2, bias=False) self.B.weight = nn.Parameter(B) self.x0 = nn.Parameter(x0) def forward(self, x, t): xTx0 = torch.sum(x*self.x0, dim=1) dxdt = torch.sigmoid(xTx0) * self.A(x - self.x0) + torch.sigmoid(-xTx0) * self.B(x + self.x0) return dxdt

Dinámica de aprendizaje en forma de una red totalmente conectada.

 class NNODEF(ODEF): def __init__(self, in_dim, hid_dim, time_invariant=False): super(NNODEF, self).__init__() self.time_invariant = time_invariant if time_invariant: self.lin1 = nn.Linear(in_dim, hid_dim) else: self.lin1 = nn.Linear(in_dim+1, hid_dim) self.lin2 = nn.Linear(hid_dim, hid_dim) self.lin3 = nn.Linear(hid_dim, in_dim) self.elu = nn.ELU(inplace=True) def forward(self, x, t): if not self.time_invariant: x = torch.cat((x, t), dim=-1) h = self.elu(self.lin1(x)) h = self.elu(self.lin2(h)) out = self.lin3(h) return out def to_np(x): return x.detach().cpu().numpy() def plot_trajectories(obs=None, times=None, trajs=None, save=None, figsize=(16, 8)): plt.figure(figsize=figsize) if obs is not None: if times is None: times = [None] * len(obs) for o, t in zip(obs, times): o, t = to_np(o), to_np(t) for b_i in range(o.shape[1]): plt.scatter(o[:, b_i, 0], o[:, b_i, 1], c=t[:, b_i, 0], cmap=cm.plasma) if trajs is not None: for z in trajs: z = to_np(z) plt.plot(z[:, 0, 0], z[:, 0, 1], lw=1.5) if save is not None: plt.savefig(save) plt.show() def conduct_experiment(ode_true, ode_trained, n_steps, name, plot_freq=10): # Create data z0 = Variable(torch.Tensor([[0.6, 0.3]])) t_max = 6.29*5 n_points = 200 index_np = np.arange(0, n_points, 1, dtype=np.int) index_np = np.hstack([index_np[:, None]]) times_np = np.linspace(0, t_max, num=n_points) times_np = np.hstack([times_np[:, None]]) times = torch.from_numpy(times_np[:, :, None]).to(z0) obs = ode_true(z0, times, return_whole_sequence=True).detach() obs = obs + torch.randn_like(obs) * 0.01 # Get trajectory of random timespan min_delta_time = 1.0 max_delta_time = 5.0 max_points_num = 32 def create_batch(): t0 = np.random.uniform(0, t_max - max_delta_time) t1 = t0 + np.random.uniform(min_delta_time, max_delta_time) idx = sorted(np.random.permutation( index_np[(times_np > t0) & (times_np < t1)] )[:max_points_num]) obs_ = obs[idx] ts_ = times[idx] return obs_, ts_ # Train Neural ODE optimizer = torch.optim.Adam(ode_trained.parameters(), lr=0.01) for i in range(n_steps): obs_, ts_ = create_batch() z_ = ode_trained(obs_[0], ts_, return_whole_sequence=True) loss = F.mse_loss(z_, obs_.detach()) optimizer.zero_grad() loss.backward(retain_graph=True) optimizer.step() if i % plot_freq == 0: z_p = ode_trained(z0, times, return_whole_sequence=True) plot_trajectories(obs=[obs], times=[times], trajs=[z_p], save=f"assets/imgs/{name}/{i}.png") clear_output(wait=True) ode_true = NeuralODE(SpiralFunctionExample()) ode_trained = NeuralODE(RandomLinearODEF()) conduct_experiment(ode_true, ode_trained, 500, "linear") func = TestODEF(Tensor([[-0.1, -0.5], [0.5, -0.1]]), Tensor([[0.2, 1.], [-1, 0.2]]), Tensor([[-1., 0.]])) ode_true = NeuralODE(func) func = NNODEF(2, 16, time_invariant=True) ode_trained = NeuralODE(func) conduct_experiment(ode_true, ode_trained, 3000, "comp", plot_freq=30)

Como puede ver, Neural ODE es bastante bueno para restaurar la dinámica. Es decir, el concepto en su conjunto funciona.
Ahora verifique un problema un poco más complicado (MNIST, jaja).

ODE neuronal inspirada en ResNets

En ResNet'ax, el estado latente cambia de acuerdo con la fórmula

$h_ {t + 1} = h_ {t} + f (h_ {t}, \ theta_ {t})$

donde $t \ in \ {0 ... T \}$ Es el número de bloque y

Esta es una función aprendida por las capas dentro del bloque.

En el límite, si tomamos un número infinito de bloques con pasos cada vez más pequeños, obtenemos la dinámica continua de la capa oculta en forma de ODE, al igual que lo que estaba arriba.

$\ frac {dh (t)} {dt} = f (h (t), t, \ theta)$

Comenzando desde la capa de entrada h (0)

podemos definir la capa de salida h (T)

como una solución a esta ODE en el momento T.

Ahora podemos contar $\ theta$ como parámetros distribuidos ( compartidos ) entre todos los bloques infinitesimales.

Validación de la arquitectura neuronal ODE en MNIST

En esta parte, probaremos la capacidad de Neural ODE para usarse como componentes en arquitecturas más familiares.

En particular, reemplazaremos los bloques residuales con ODE neuronal en el clasificador MNIST.

Código

 def norm(dim): return nn.BatchNorm2d(dim) def conv3x3(in_feats, out_feats, stride=1): return nn.Conv2d(in_feats, out_feats, kernel_size=3, stride=stride, padding=1, bias=False) def add_time(in_tensor, t): bs, c, w, h = in_tensor.shape return torch.cat((in_tensor, t.expand(bs, 1, w, h)), dim=1) class ConvODEF(ODEF): def __init__(self, dim): super(ConvODEF, self).__init__() self.conv1 = conv3x3(dim + 1, dim) self.norm1 = norm(dim) self.conv2 = conv3x3(dim + 1, dim) self.norm2 = norm(dim) def forward(self, x, t): xt = add_time(x, t) h = self.norm1(torch.relu(self.conv1(xt))) ht = add_time(h, t) dxdt = self.norm2(torch.relu(self.conv2(ht))) return dxdt class ContinuousNeuralMNISTClassifier(nn.Module): def __init__(self, ode): super(ContinuousNeuralMNISTClassifier, self).__init__() self.downsampling = nn.Sequential( nn.Conv2d(1, 64, 3, 1), norm(64), nn.ReLU(inplace=True), nn.Conv2d(64, 64, 4, 2, 1), norm(64), nn.ReLU(inplace=True), nn.Conv2d(64, 64, 4, 2, 1), ) self.feature = ode self.norm = norm(64) self.avg_pool = nn.AdaptiveAvgPool2d((1, 1)) self.fc = nn.Linear(64, 10) def forward(self, x): x = self.downsampling(x) x = self.feature(x) x = self.norm(x) x = self.avg_pool(x) shape = torch.prod(torch.tensor(x.shape[1:])).item() x = x.view(-1, shape) out = self.fc(x) return out func = ConvODEF(64) ode = NeuralODE(func) model = ContinuousNeuralMNISTClassifier(ode) if use_cuda: model = model.cuda() import torchvision img_std = 0.3081 img_mean = 0.1307 batch_size = 32 train_loader = torch.utils.data.DataLoader( torchvision.datasets.MNIST("data/mnist", train=True, download=True, transform=torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((img_mean,), (img_std,)) ]) ), batch_size=batch_size, shuffle=True ) test_loader = torch.utils.data.DataLoader( torchvision.datasets.MNIST("data/mnist", train=False, download=True, transform=torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((img_mean,), (img_std,)) ]) ), batch_size=128, shuffle=True ) optimizer = torch.optim.Adam(model.parameters()) def train(epoch): num_items = 0 train_losses = [] model.train() criterion = nn.CrossEntropyLoss() print(f"Training Epoch {epoch}...") for batch_idx, (data, target) in tqdm(enumerate(train_loader), total=len(train_loader)): if use_cuda: data = data.cuda() target = target.cuda() optimizer.zero_grad() output = model(data) loss = criterion(output, target) loss.backward() optimizer.step() train_losses += [loss.item()] num_items += data.shape[0] print('Train loss: {:.5f}'.format(np.mean(train_losses))) return train_losses def test(): accuracy = 0.0 num_items = 0 model.eval() criterion = nn.CrossEntropyLoss() print(f"Testing...") with torch.no_grad(): for batch_idx, (data, target) in tqdm(enumerate(test_loader), total=len(test_loader)): if use_cuda: data = data.cuda() target = target.cuda() output = model(data) accuracy += torch.sum(torch.argmax(output, dim=1) == target).item() num_items += data.shape[0] accuracy = accuracy * 100 / num_items print("Test Accuracy: {:.3f}%".format(accuracy)) n_epochs = 5 test() train_losses = [] for epoch in range(1, n_epochs + 1): train_losses += train(epoch) test() import pandas as pd plt.figure(figsize=(9, 5)) history = pd.DataFrame({"loss": train_losses}) history["cum_data"] = history.index * batch_size history["smooth_loss"] = history.loss.ewm(halflife=10).mean() history.plot(x="cum_data", y="smooth_loss", figsize=(12, 5), title="train error")

 Testing... 100% 79/79 [00:01<00:00, 45.69it/s] Test Accuracy: 9.740% Training Epoch 1... 100% 1875/1875 [01:15<00:00, 24.69it/s] Train loss: 0.20137 Testing... 100% 79/79 [00:01<00:00, 46.64it/s] Test Accuracy: 98.680% Training Epoch 2... 100% 1875/1875 [01:17<00:00, 24.32it/s] Train loss: 0.05059 Testing... 100% 79/79 [00:01<00:00, 46.11it/s] Test Accuracy: 97.760% Training Epoch 3... 100% 1875/1875 [01:16<00:00, 24.63it/s] Train loss: 0.03808 Testing... 100% 79/79 [00:01<00:00, 45.65it/s] Test Accuracy: 99.000% Training Epoch 4... 100% 1875/1875 [01:17<00:00, 24.28it/s] Train loss: 0.02894 Testing... 100% 79/79 [00:01<00:00, 45.42it/s] Test Accuracy: 99.130% Training Epoch 5... 100% 1875/1875 [01:16<00:00, 24.67it/s] Train loss: 0.02424 Testing... 100% 79/79 [00:01<00:00, 45.89it/s] Test Accuracy: 99.170%

Después de un entrenamiento muy duro durante solo 5 eras y 6 minutos de entrenamiento, el modelo ya ha alcanzado un error de prueba de menos del 1%. Podemos decir que las ODE neuronales se integran bien como un componente en redes más tradicionales.

En su artículo, los autores también comparan este clasificador (ODE-Net) con una red normal totalmente conectada, con ResNet con una arquitectura similar y con la misma arquitectura exacta, en la que el gradiente se propaga directamente a través de operaciones en ODESolve (sin el método de gradiente conjugado) ( RK-Net).

Ilustración del artículo original.

Según ellos, una red de 1 capa totalmente conectada con aproximadamente el mismo número de parámetros que Neural ODE tiene un error mucho mayor en la prueba, ResNet con el mismo error tiene muchos más parámetros, y RK-Net sin el método de gradiente conjugado tiene un error ligeramente mayor y con un consumo de memoria que aumenta linealmente (cuanto menor es el error permitido, más pasos debe seguir ODESolve , lo que aumenta linealmente el consumo de memoria con el número de pasos).

Los autores utilizan el método implícito Runge-Kutta con un tamaño de paso adaptativo en su implementación, a diferencia del método más simple de Euler aquí. También estudian algunas propiedades de la nueva arquitectura.

Función ODE-Net (NFE Forward - el número de cálculos de funciones en un pase directo)
Ilustración del artículo original.

(a) Cambiar el nivel aceptable de error numérico cambia el número de pasos en la distribución directa.
(b) El tiempo dedicado a la distribución directa es proporcional al número de cálculos de la función.
(c) El número de cálculos de la función para la propagación inversa es aproximadamente la mitad de la propagación directa, lo que indica que el método de gradiente conjugado puede ser más eficiente computacionalmente que propagar el gradiente directamente a través de ODESolve .
(d) A medida que ODE-Net se entrena cada vez más, requiere más y más cálculos de una función (un paso cada vez más pequeño), posiblemente adaptándose a la creciente complejidad del modelo.

Función Generadora Oculta para Modelado de Series de Tiempo

Neural ODE es adecuado para procesar datos en serie continuos incluso cuando la ruta se encuentra en un espacio oculto desconocido.

En esta sección, experimentaremos y cambiaremos la generación de secuencias continuas usando Neural ODE , y observaremos el espacio oculto aprendido.

Los autores también comparan esto con secuencias similares generadas por redes recurrentes.

El experimento aquí es ligeramente diferente del ejemplo correspondiente en el repositorio de autores, aquí hay un conjunto más diverso de caminos.

Datos

Los datos de entrenamiento consisten en espirales aleatorias, la mitad de las cuales son en sentido horario, y la segunda en sentido antihorario. Además, las subsecuencias aleatorias se muestrean a partir de estas espirales, procesadas por el modelo de recurrencia de codificación en la dirección opuesta, dando lugar a un estado oculto inicial, que luego evoluciona, creando una trayectoria en el espacio oculto. Esta ruta latente se asigna al espacio de datos y se compara con la subsecuencia muestreada. Por lo tanto, el modelo aprende a generar rutas similares a un conjunto de datos.

Ejemplos de espirales de conjuntos de datos

VAE como modelo generativo

Modelo generativo a través de un procedimiento de muestreo:

$z_ {t_0} \ sim \ mathcal {N} (0, I)$

$z_ {t_1}, z_ {t_2}, ..., z_ {t_M} = \ text {ODESolve} (z_ {t_0}, f, \ theta_f, t_0, ..., t_M)$

$x_ {t_i} \ sim p (x \ mid z_ {t_i}; \ theta_x)$

Que se puede entrenar usando el enfoque variador de codificador automático.

Ir a través de un codificador recurrente a través de una secuencia de tiempo en el tiempo para obtener los parámetros $\ mu_ {z_ {t_0}}$ , $\ sigma_ {z_ {t_0}}$ distribución posterior variacional, y luego muestra de ella:

$z_ {t_0} \ sim q \ left (z_ {t_0} \ mid x_ {t_0}, ..., x_ {t_M}; t_0, ..., t_M; \ theta_q \ right) = \ mathcal {N} \ izquierda (z_ {t_0} \ mid \ mu_ {z_ {t_0}} \ sigma_ {z_ {t_0}} \ right)$

Obtener trayectoria oculta:

$z_ {t_1}, z_ {t_2}, ..., z_ {t_N} = \ text {ODESolve} (z_ {t_0}, f, \ theta_f, t_0, ..., t_N), \ text {where} \ frac {dz} {dt} = f (z, t; \ theta_f)$

Asigne una ruta oculta a una ruta en los datos utilizando otra red neuronal: $\ hat {x_ {t_i}} (z_ {t_i}, t_i; \ theta_x)$
Maximice la evaluación del límite inferior de validez (ELBO) para la ruta muestreada:

$\ text {ELBO} \ approx N \ Big (\ sum_ {i = 0} ^ {M} \ log p (x_ {t_i} \ mid z_ {t_i} (z_ {t_0}; \ theta_f); \ theta_x) + KL \ left (q (z_ {t_0} \ mid x_ {t_0}, ..., x_ {t_M}; t_0, ..., t_M; \ theta_q) \ parallel \ mathcal {N} (0, I) \ derecha) \ Big)$

Y en el caso de una distribución posterior gaussiana $p (x \ mid z_ {t_i}; \ theta_x)$ y nivel de ruido conocido $\ sigma_x$ :

$\ text {ELBO} \ approx -N \ Big (\ sum_ {i = 1} ^ {M} \ frac {(x_i - \ hat {x_i}) ^ 2} {\ sigma_x ^ 2} - \ log \ sigma_ { z_ {t_0}} ^ 2 + \ mu_ {z_ {t_0}} ^ 2 + \ sigma_ {z_ {t_0}} ^ 2 \ Big) + C$

El gráfico de cálculo de un modelo ODE oculto se puede representar de la siguiente manera

Ilustración del artículo original.

Este modelo se puede probar para ver cómo interpola la ruta utilizando solo las observaciones iniciales.

Código

Definir modelos

 class RNNEncoder(nn.Module): def __init__(self, input_dim, hidden_dim, latent_dim): super(RNNEncoder, self).__init__() self.input_dim = input_dim self.hidden_dim = hidden_dim self.latent_dim = latent_dim self.rnn = nn.GRU(input_dim+1, hidden_dim) self.hid2lat = nn.Linear(hidden_dim, 2*latent_dim) def forward(self, x, t): # Concatenate time to input t = t.clone() t[1:] = t[:-1] - t[1:] t[0] = 0. xt = torch.cat((x, t), dim=-1) _, h0 = self.rnn(xt.flip((0,))) # Reversed # Compute latent dimension z0 = self.hid2lat(h0[0]) z0_mean = z0[:, :self.latent_dim] z0_log_var = z0[:, self.latent_dim:] return z0_mean, z0_log_var class NeuralODEDecoder(nn.Module): def __init__(self, output_dim, hidden_dim, latent_dim): super(NeuralODEDecoder, self).__init__() self.output_dim = output_dim self.hidden_dim = hidden_dim self.latent_dim = latent_dim func = NNODEF(latent_dim, hidden_dim, time_invariant=True) self.ode = NeuralODE(func) self.l2h = nn.Linear(latent_dim, hidden_dim) self.h2o = nn.Linear(hidden_dim, output_dim) def forward(self, z0, t): zs = self.ode(z0, t, return_whole_sequence=True) hs = self.l2h(zs) xs = self.h2o(hs) return xs class ODEVAE(nn.Module): def __init__(self, output_dim, hidden_dim, latent_dim): super(ODEVAE, self).__init__() self.output_dim = output_dim self.hidden_dim = hidden_dim self.latent_dim = latent_dim self.encoder = RNNEncoder(output_dim, hidden_dim, latent_dim) self.decoder = NeuralODEDecoder(output_dim, hidden_dim, latent_dim) def forward(self, x, t, MAP=False): z_mean, z_log_var = self.encoder(x, t) if MAP: z = z_mean else: z = z_mean + torch.randn_like(z_mean) * torch.exp(0.5 * z_log_var) x_p = self.decoder(z, t) return x_p, z, z_mean, z_log_var def generate_with_seed(self, seed_x, t): seed_t_len = seed_x.shape[0] z_mean, z_log_var = self.encoder(seed_x, t[:seed_t_len]) x_p = self.decoder(z_mean, t) return x_p

Generación de conjunto de datos

 t_max = 6.29*5 n_points = 200 noise_std = 0.02 num_spirals = 1000 index_np = np.arange(0, n_points, 1, dtype=np.int) index_np = np.hstack([index_np[:, None]]) times_np = np.linspace(0, t_max, num=n_points) times_np = np.hstack([times_np[:, None]] * num_spirals) times = torch.from_numpy(times_np[:, :, None]).to(torch.float32) # Generate random spirals parameters normal01 = torch.distributions.Normal(0, 1.0) x0 = Variable(normal01.sample((num_spirals, 2))) * 2.0 W11 = -0.1 * normal01.sample((num_spirals,)).abs() - 0.05 W22 = -0.1 * normal01.sample((num_spirals,)).abs() - 0.05 W21 = -1.0 * normal01.sample((num_spirals,)).abs() W12 = 1.0 * normal01.sample((num_spirals,)).abs() xs_list = [] for i in range(num_spirals): if i % 2 == 1: # Make it counter-clockwise W21, W12 = W12, W21 func = LinearODEF(Tensor([[W11[i], W12[i]], [W21[i], W22[i]]])) ode = NeuralODE(func) xs = ode(x0[i:i+1], times[:, i:i+1], return_whole_sequence=True) xs_list.append(xs) orig_trajs = torch.cat(xs_list, dim=1).detach() samp_trajs = orig_trajs + torch.randn_like(orig_trajs) * noise_std samp_ts = times fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(15, 9)) axes = axes.flatten() for i, ax in enumerate(axes): ax.scatter(samp_trajs[:, i, 0], samp_trajs[:, i, 1], c=samp_ts[:, i, 0], cmap=cm.plasma) plt.show() import numpy.random as npr def gen_batch(batch_size, n_sample=100): n_batches = samp_trajs.shape[1] // batch_size time_len = samp_trajs.shape[0] n_sample = min(n_sample, time_len) for i in range(n_batches): if n_sample > 0: probs = [1. / (time_len - n_sample)] * (time_len - n_sample) t0_idx = npr.multinomial(1, probs) t0_idx = np.argmax(t0_idx) tM_idx = t0_idx + n_sample else: t0_idx = 0 tM_idx = time_len frm, to = batch_size*i, batch_size*(i+1) yield samp_trajs[t0_idx:tM_idx, frm:to], samp_ts[t0_idx:tM_idx, frm:to]

Entrenamiento

 vae = ODEVAE(2, 64, 6) vae = vae.cuda() if use_cuda: vae = vae.cuda() optim = torch.optim.Adam(vae.parameters(), betas=(0.9, 0.999), lr=0.001) preload = False n_epochs = 20000 batch_size = 100 plot_traj_idx = 1 plot_traj = orig_trajs[:, plot_traj_idx:plot_traj_idx+1] plot_obs = samp_trajs[:, plot_traj_idx:plot_traj_idx+1] plot_ts = samp_ts[:, plot_traj_idx:plot_traj_idx+1] if use_cuda: plot_traj = plot_traj.cuda() plot_obs = plot_obs.cuda() plot_ts = plot_ts.cuda() if preload: vae.load_state_dict(torch.load("models/vae_spirals.sd")) for epoch_idx in range(n_epochs): losses = [] train_iter = gen_batch(batch_size) for x, t in train_iter: optim.zero_grad() if use_cuda: x, t = x.cuda(), t.cuda() max_len = np.random.choice([30, 50, 100]) permutation = np.random.permutation(t.shape[0]) np.random.shuffle(permutation) permutation = np.sort(permutation[:max_len]) x, t = x[permutation], t[permutation] x_p, z, z_mean, z_log_var = vae(x, t) z_var = torch.exp(z_log_var) kl_loss = -0.5 * torch.sum(1 + z_log_var - z_mean**2 - z_var, -1) loss = 0.5 * ((x-x_p)**2).sum(-1).sum(0) / noise_std**2 + kl_loss loss = torch.mean(loss) loss /= max_len loss.backward() optim.step() losses.append(loss.item()) print(f"Epoch {epoch_idx}") frm, to, to_seed = 0, 200, 50 seed_trajs = samp_trajs[frm:to_seed] ts = samp_ts[frm:to] if use_cuda: seed_trajs = seed_trajs.cuda() ts = ts.cuda() samp_trajs_p = to_np(vae.generate_with_seed(seed_trajs, ts)) fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(15, 9)) axes = axes.flatten() for i, ax in enumerate(axes): ax.scatter(to_np(seed_trajs[:, i, 0]), to_np(seed_trajs[:, i, 1]), c=to_np(ts[frm:to_seed, i, 0]), cmap=cm.plasma) ax.plot(to_np(orig_trajs[frm:to, i, 0]), to_np(orig_trajs[frm:to, i, 1])) ax.plot(samp_trajs_p[:, i, 0], samp_trajs_p[:, i, 1]) plt.show() print(np.mean(losses), np.median(losses)) clear_output(wait=True) spiral_0_idx = 3 spiral_1_idx = 6 homotopy_p = Tensor(np.linspace(0., 1., 10)[:, None]) vae = vae if use_cuda: homotopy_p = homotopy_p.cuda() vae = vae.cuda() spiral_0 = orig_trajs[:, spiral_0_idx:spiral_0_idx+1, :] spiral_1 = orig_trajs[:, spiral_1_idx:spiral_1_idx+1, :] ts_0 = samp_ts[:, spiral_0_idx:spiral_0_idx+1, :] ts_1 = samp_ts[:, spiral_1_idx:spiral_1_idx+1, :] if use_cuda: spiral_0, ts_0 = spiral_0.cuda(), ts_0.cuda() spiral_1, ts_1 = spiral_1.cuda(), ts_1.cuda() z_cw, _ = vae.encoder(spiral_0, ts_0) z_cc, _ = vae.encoder(spiral_1, ts_1) homotopy_z = z_cw * (1 - homotopy_p) + z_cc * homotopy_p t = torch.from_numpy(np.linspace(0, 6*np.pi, 200)) t = t[:, None].expand(200, 10)[:, :, None].cuda() t = t.cuda() if use_cuda else t hom_gen_trajs = vae.decoder(homotopy_z, t) fig, axes = plt.subplots(nrows=2, ncols=5, figsize=(15, 5)) axes = axes.flatten() for i, ax in enumerate(axes): ax.plot(to_np(hom_gen_trajs[:, i, 0]), to_np(hom_gen_trajs[:, i, 1])) plt.show() torch.save(vae.state_dict(), "models/vae_spirals.sd")

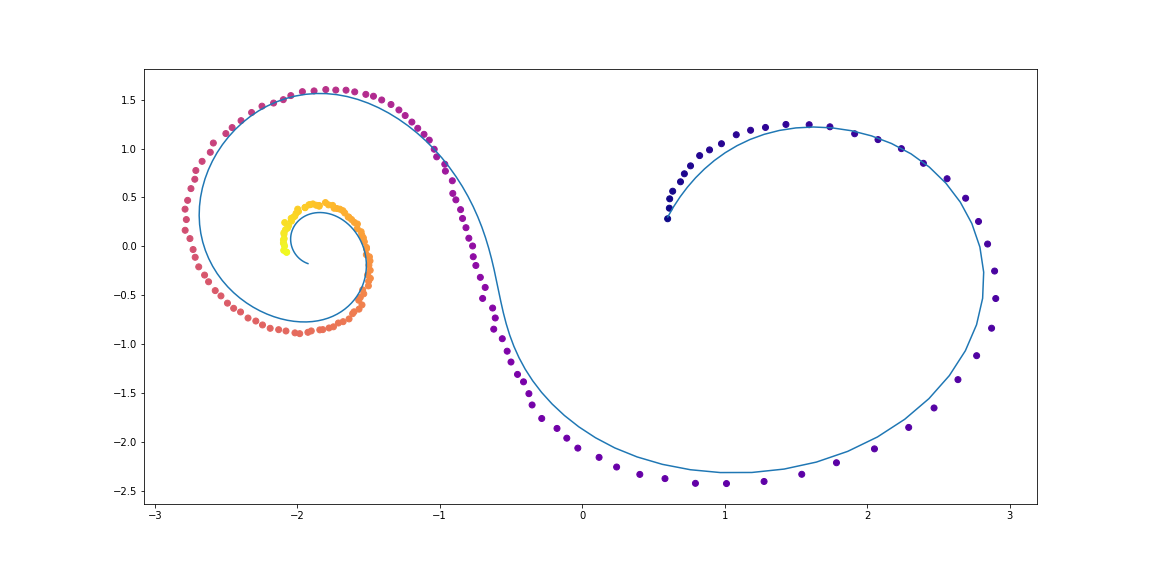
Eso es lo que sucede después de una noche de entrenamiento.

Los puntos son observaciones ruidosas de la trayectoria original (azul), el
amarillo son trayectorias reconstruidas e interpoladas, utilizando puntos como entradas.

El color del punto muestra el tiempo.

Las reconstrucciones de algunos ejemplos no se ven muy bien. Tal vez el modelo no sea lo suficientemente complejo o no se estudie lo suficiente. En cualquier caso, la reconstrucción parece muy razonable.

Ahora veamos qué sucede si interpolamos una variable oculta en una trayectoria en sentido horario a una trayectoria en sentido antihorario.

Los autores también comparan las reconstrucciones y las interpolaciones de ruta entre ODE neuronal y una red recursiva simple.

Ilustración del artículo original.

Corrientes de normalización continua

El artículo original también aporta mucho al tema de Normalización de flujos. Los flujos de normalización se utilizan cuando necesita muestrear a partir de una distribución compleja que aparece a través del cambio de variables a partir de una distribución simple (gaussiana, por ejemplo), y aún así conocer la densidad de probabilidad en el punto de cada muestra.
Los autores muestran que el uso de la sustitución continua de variables es mucho más computacionalmente eficiente e interpretable que los métodos anteriores.

Los flujos de normalización son muy útiles en modelos como Variation AutoCoders , Bayesian Neural Networks y otros del enfoque bayesiano.

Este tema, sin embargo, queda fuera del alcance de esteartículos, y aquellos que estén interesados deben leer el artículo científico original.

Para semillas:

Visualización de la transformación de ruido (distribución simple) a datos (distribución compleja) para dos conjuntos de datos;

El eje X muestra la transformación de la densidad y las muestras en el transcurso del "tiempo" (para NS) y la "profundidad" (para NS).

Ilustración del artículo original

Gracias a bekemax por su ayuda en la edición de la versión en inglés del texto y por sus interesantes comentarios físicos.

Esto concluye mi pequeña investigación sobre las EDO neurales . Gracias por su atencion!

Introduciendo Neural ODE

Ecuaciones diferenciales ordinarias neurales

Planteamiento del problema

Implementación

Solicitud

Recuperación de la función dinámica real (verificación de aproximación)

ODE neuronal inspirada en ResNets

Validación de la arquitectura neuronal ODE en MNIST

Función Generadora Oculta para Modelado de Series de Tiempo

Datos

VAE como modelo generativo

Definir modelos

Generación de conjunto de datos

Entrenamiento

Corrientes de normalización continua

Enlaces utiles

More articles: