Tareas del libro de texto escolar II

Parte 1
Parte II
Parte III

Este artículo analiza el método para estimar el rango de valores aceptados y la relación de este método con las tareas que contienen un módulo.

Al resolver algunos problemas, es necesario considerar el rango dentro del cual puede estar el valor deseado.

Considere el método de estimación para resolver desigualdades.

Suponga que el precio por unidad de bienes puede variar de 5 a 10 RUB. Dar un límite superior significa determinar el valor máximo que puede tomar la cantidad deseada. Para dos unidades de bienes, cuyo precio no exceda de 10, la estimación superior será 10 + 10 = 20 .

Considere el problema del perfil de perfil de problema MI Bashmakova
37. Estimaciones conocidas para variables $$$x$ y$$ $ en línea $ y: 0 <x <5, 2 <y <3. $ en línea $

Dé las mejores notas para las siguientes expresiones:
1) $$$2x + 3y$
2) $$$xy$

5) $$$\ frac {1} {y}$
6) $$$\ frac {x} {y}$

8) $$$x-y$
9) $$$3x-2y$


En general, el análisis de cantidades infinitesimales utiliza un criterio de evaluación. Un módulo (como vecindario) encuentra aplicación en la definición de un límite.

$$$$ display $$ \ left | x_ {n} -a \ right | <\ varepsilon $$ display $$

Considere el ejemplo del "Curso de cálculo diferencial e integral" 363 (6)

Divergencia de filas fácil de configurar

$$

$$\ sum \ frac {1} {\ sqrt {n}} = 1+ \ frac {1} {\ sqrt {2}} + \ frac {1} {\ sqrt {3}} + ... + \ frac {1} {\ sqrt {n}} + ...$$

De hecho, dado que sus miembros disminuyen, la enésima suma parcial

$$$$ display $$ 1+ \ frac {1} {\ sqrt {2}} + ... + \ frac {1} {\ sqrt {n}}> n \ cdot \ frac {1} {\ sqrt {n }} = \ sqrt {n} $$ mostrar $$

y crece hasta el infinito con $$$n$ .

Para probar que $$$1+ \ frac {1} {\ sqrt {2}} + ... + \ frac {1} {\ sqrt {n}}$ realmente más $$$\ sqrt {n}$ , necesita hacer una estimación más baja de esta expresión. Obtenemos el sistema de desigualdades

$$$$ display $$ \ left \ {\! \ begin {alineado} & \ frac {1} {\ sqrt {n-1}}> \ frac {1} {\ sqrt {n}} \\ & \ frac { 1} {\ sqrt {n-2}}> \ frac {1} {\ sqrt {n}} \\ & \ frac {1} {\ sqrt {n-3}}> \ frac {1} {\ sqrt {n}} \\ & ... \ end {alineado} \ right. $$ display $$

Después de agregar todas las desigualdades de este sistema, obtenemos

$$$$ display $$ 1+ \ frac {1} {\ sqrt {2}} + \ frac {1} {\ sqrt {3}} + ... + \ frac {1} {\ sqrt {n}}> \ frac {1} {\ sqrt {n}} + \ frac {1} {\ sqrt {n}} + \ frac {1} {\ sqrt {n}} + ... + \ frac {1} {\ sqrt {n}} = n \ cdot \ frac {1} {\ sqrt {n}} $$ display $$

Esta es una prueba de que esta serie diverge.

Para una serie armónica, este método no funciona porque $$$n$ serie parcial parcial armónica

$$$$ display $$ 1+ \ frac {1} {2} + \ frac {1} {3} + ... + \ frac {1} {n}> n \ cdot \ frac {1} {n} = 1 $$ pantalla $$

De vuelta a la tarea

38. Calcule la cantidad ("Tareas para niños de 5 a 15 años")

$$

$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3} + \ frac {1} {3 \ cdot4} + ... + \ frac {1} {99 \ cdot100}$$

(con un error de no más del 1% de la respuesta)

Estimación superior de la serie. $$$\ frac {n} {n + 1}$ da el número 1.

Suelta el primer término $$$\ frac {1} {1 \ cdot2}$

(define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* (+ n 1.0 )(+ n 2.0))) (series_sum_1(- n 1.0))) ) ) ) (writeln (series_sum_1 10)) (writeln (series_sum_1 100)) (writeln (series_sum_1 1000)) (writeln (series_sum_1 10000)) (writeln (series_sum_1 100000)) (writeln (series_sum_1 1000000)) 

Nosotros obtenemos $$$1 - \ frac {1} {1 \ cdot2} = \ frac {1} {2}$
0.4166666666666666363
0.49019607843137253
0.4990019960079833
0.4999000199960005
0.49999000019998724
0.4999990000019941

Puedes consultar ideone.com aquí


Suelta los primeros dos términos $$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3}$

 (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* (+ n 2.0) (+ n 3.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 1000000) 

Obtendremos 0.33333233333632745
Sumas parciales de la serie están limitadas arriba.

La fila positiva siempre tiene una cantidad; esta suma será finita (y, por lo tanto, la serie converge) si las sumas parciales de la serie están limitadas arriba, e infinita (y la serie diverge) de lo contrario.

Tirar $$$n$ términos iniciales de la serie armónica.
Probar (usando el límite inferior) que

$$$$ display $$ \ frac {1} {n + 1} + \ frac {1} {n + 2} + ... + \ frac {1} {2n}> \ frac {1} {2} $$ mostrar $$

Si, descartando los dos primeros términos, los miembros restantes de la serie armónica se dividen en grupos por $$$2,4,8, ..., 2 ^ {k-1}, ...$ miembros en cada

$$

$$\ frac {1} {3} + \ frac {1} {4}; \ frac {1} {5} + \ frac {1} {6} + \ frac {1} {7} + \ frac {1} {8}; \ frac {1} {9} + ... \ frac {1} {16}; ...; $$$

$$

$$\ frac {1} {2 ^ {k-1} +1} + ... + \ frac {1} {2 ^ {k}}; ...,$$

entonces cada una de estas cantidades individualmente será mayor $$$\ frac {1} {2}$ .
... Vemos que las sumas parciales no se pueden acotar arriba: la serie tiene una suma infinita.

Calculamos las cantidades parciales que se obtienen descartando $$$2 ^ {k}$ términos

 #lang racket (* 1.0 (+ 1/3 1/4)) (* 1.0 (+ 1/5 1/6 1/7 1/8)) (* 1.0 (+ 1/9 1/10 1/11 1/12 1/13 1/14 1/15 1/16)) 

Obtenemos:
0.583333333333333434
0.6345238095238095
0.6628718503718504
Escribimos un programa que calcula la suma de las series armónicas de $$$\ frac {n} {2}$ antes $$$n$ donde $$$n = 2 ^ {k}$ a las $$$k \ in \ mathbb {N}$

 #lang racket (define (Hn n ) (define half_arg (/ n 2.0)) (define (series_sum n) (if (= n half_arg ) 0 (+ (/ 1.0 n) (series_sum(- n 1)) ) ) ) (series_sum n) ) (Hn 4) (Hn 8) (Hn 16) (Hn 32) 

Obtenemos:
0.583333333333333333
0.6345238095238095
0.6628718503718504
0.6777662022075267

Puede consultar ide en línea en el enlace
Para el rango $$$\ left [1 + 2 ^ {70}; 2 ^ {71} \ right]$ obtenemos 0.693147 ...
Mira el mojo en Wolfram Cloud aquí .

Este algoritmo recursivo provoca un desbordamiento rápido de la pila.
Este artículo tiene un ejemplo de cálculo factorial usando un algoritmo iterativo. Modificamos este algoritmo iterativo para que calcule la suma parcial Hn dentro de ciertos límites; llamar a estos límites ayb

 (define (Hn ab) (define (iteration product counter) (if (> counter b) product (iteration (+ product (/ 1.0 counter)) (+ counter 1)))) (iteration 0 a)) 

El límite inferior es el número $$$1 + 2 ^ {k}$ , el límite superior es el número $$$2 \ cdot 2 ^ {k}$
Escribimos una función que calcula el poder de dos

 (define (power_of_two k) (define (iteration product counter) (if (> counter k) product (iteration (* product 2) (+ counter 1)))) (iteration 1 1)) 

Sustituiremos (+ 1 (power_of_two k)) como límite inferior, y utilizaremos la función (* 2 (power_of_two k)) o su función equivalente (power_of_two (+ 1 k)) como límite superior
Reescribe la función Hn

 (define (Hn k) (define a (+ 1 (power_of_two k)) ) (define b (* 2 (power_of_two k)) ) (define (iteration product counter) (if (> counter b) product (iteration (+ product (/ 1.0 counter)) (+ counter 1)))) (iteration 0 a )) 

Ahora puede calcular Hn para valores grandes $$$k$ .

Escribimos en C un programa que mide el tiempo requerido para calcular Hn . Utilizaremos la función clock () de la biblioteca estándar <time.h>
Aquí hay un artículo sobre la medición del tiempo del procesador en Habré.

 #include <math.h> #include <stdio.h> #include <time.h> int main(int argc, char **argv) { double count; // k  1+2^30  2^31 for(unsigned long long int i=1073741825 ;i<=2147483648 ;i++) { count=count+1.0/i; } printf("Hn = %.12f ", count); double seconds = clock() / (double) CLOCKS_PER_SEC; printf("  %f  \n", seconds); return 0; } 

Por lo general, la identificación en línea limita el tiempo de ejecución de los programas en ejecución a cinco segundos, por lo que este programa solo se puede verificar en algunas identificaciones en línea, por ejemplo, en líneagdb.com o repl.it
Para k de 1 + 2 ^ 30 a 2 ^ 31, el tiempo de funcionamiento será de ~ 5 segundos.
Para k de 1 + 2 ^ 31 a 2 ^ 32, el tiempo de funcionamiento será de ~ 10 segundos.
Para k de 1 + 2 ^ 32 a 2 ^ 33, el tiempo de funcionamiento será de ~ 20 segundos.
Para k de 1 + 2 ^ 33 a 2 ^ 34, el tiempo de funcionamiento será de ~ 40 segundos.
Para k de 1 + 2 ^ 34 a 2 ^ 35, el tiempo de funcionamiento será más de un minuto.
...
Para k de 1 + 2 ^ 45 a 2 ^ 46, el tiempo de funcionamiento será superior a 24 horas.

Suponga que para k de 1 + 2 ^ 30 a 2 ^ 31, el tiempo de ejecución del algoritmo es de ~ 2 segundos.
Entonces para k = 2 ^ (30 + n) el tiempo de ejecución del algoritmo es 2 ^ n seg. (en $$$n \ in \ mathbb {N}$ )
Este algoritmo tiene una complejidad exponencial .

De vuelta a los módulos.
En cálculo integral, el módulo se usa en la fórmula

$$

$$\ int \ frac {1} {x} dx = \ int \ frac {dx} {x} = ln \ left | x \ right | + C$$

En Habré había un artículo El logaritmo más natural en el que se considera esta integral y sobre la base de su cálculo de número $$$e$ .

La presencia del módulo en la fórmula. $$$\ int \ frac {dx} {x} = ln \ left | x \ right | + C$ respaldado aún más en el "Curso de cálculo diferencial e integral"

Si ...$$ $ en línea $ x <0 $ en línea $ , entonces por diferenciación es fácil verificar que $$$\ left [ln (-x) \ right] '= \ frac {1} {x}$

Aplicación física de la integral. $$$\ int \ frac {dx} {x}$

Esta integral se usa para calcular la diferencia de potencial de las placas de un condensador cilíndrico.


"Electricidad y magnetismo":

La diferencia potencial entre las placas se encuentra mediante la integración:

$$

$$\ varphi_ {1} - \ varphi_ {2} = \ int \ limits_ {R_ {1}} ^ {R_ {2}} E (r) dr = \ frac {q} {2 \ pi \ varepsilon_ {0} \ varepsilon l} \ int \ limits_ {R_ {1}} ^ {R_ {2}} \ frac {dr} {r} = \ frac {q} {2 \ pi \ varepsilon_ {0} \ varepsilon l} ln \ frac {R_ {2}} {R_ {1}}$$

( $$$R_ {1}$ y $$$R_ {2}$ - los radios de las placas interior y exterior).

El signo del módulo no se utiliza aquí bajo el signo del logaritmo natural. $$$ln \ left | \ frac {R_ {2}} {R_ {1}} \ right | $$ porque $$$R_ {1}$ y $$$R_ {2}$ estrictamente positivo y esta forma de grabación es redundante.

Dibujo "modular"

Usando módulos, puedes dibujar varias formas.

Si en el programa de geogebra escribe la fórmula $$$abs (x) + abs (y) = 1$ tenemos



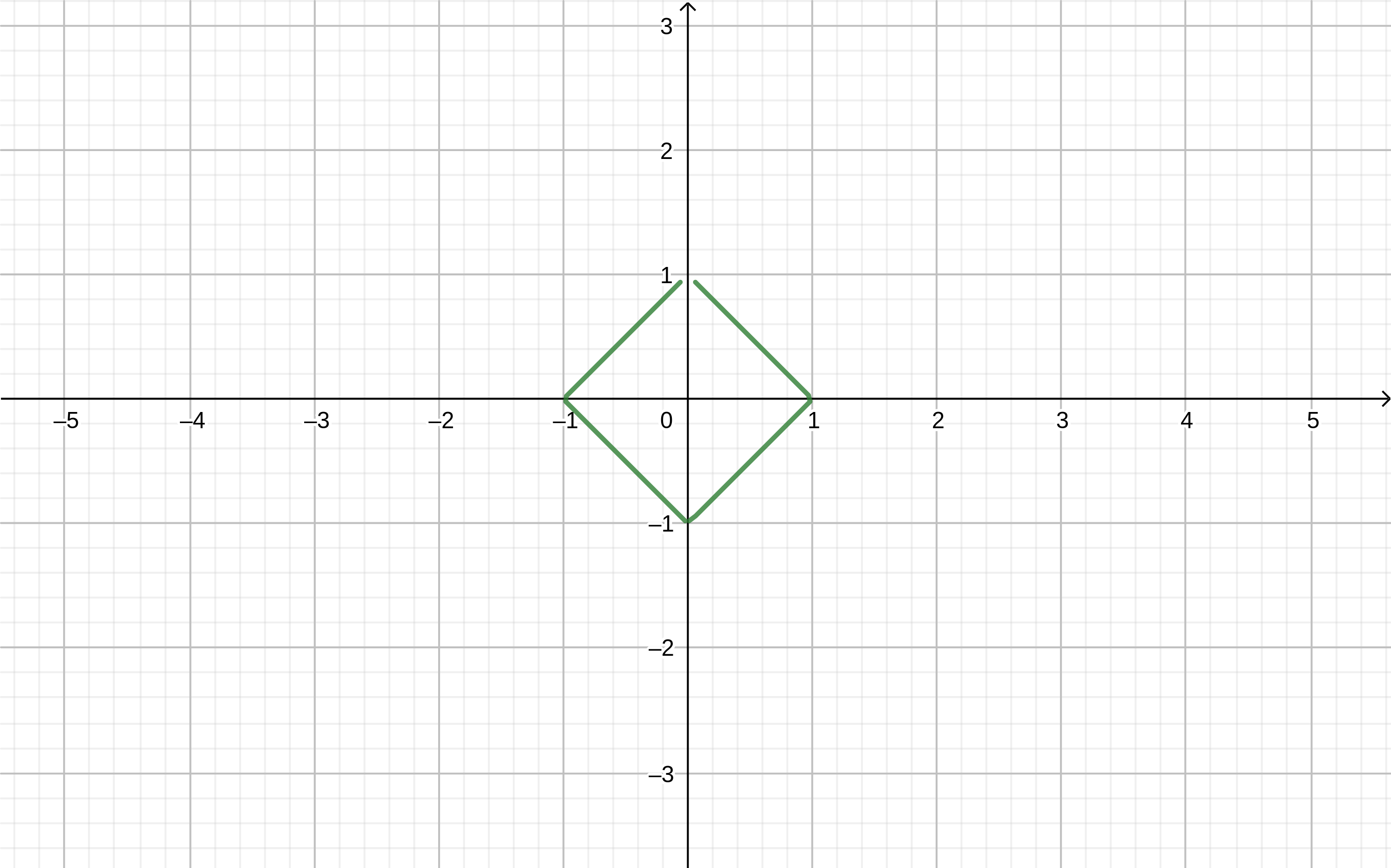
Puedes dibujar formas más complejas. Dibujemos, por ejemplo, una "mariposa" en la nube WolframAlpha

$$

$$\ sum \ frac {\ left | x \ right | } {n- \ left | x \ right | } + \ frac {\ left | x + n \ derecha | } {n} + \ frac {\ left | x-n \ right | } {n}$$

Trazar [Suma [abs (x) / (n-abs (x)) + abs (x + n) / (n) + abs (xn) / (n), {n, 1,20}], {x, -60,60}]
En esta expresion $$$n$ se encuentra en el rango de $$$1$ antes $$$20$ , $$$x$ se encuentra en el rango de $$$-60$ antes $$$60$ .
Enlace a la imagen.

Libros:

"El libro de tareas de orientación de perfil" M.I. Bashmakov
Curso de física general: en 3 volúmenes T. 2. "Electricidad y magnetismo" I.V. Savelyev