Hola Habr! Les traigo a su atenci贸n una traducci贸n del art铆culo de Rudy Gilman y Katherine Wang RL intuitiva: Introducci贸n a Advantage-Actor-Critic (A2C) .
Los especialistas en aprendizaje reforzado (RL) han producido muchos tutoriales excelentes. Sin embargo, la mayor铆a describe RL en t茅rminos de ecuaciones matem谩ticas y diagramas abstractos. Nos gusta pensar sobre el tema desde una perspectiva diferente. El RL en s铆 mismo est谩 inspirado en c贸mo aprenden los animales, entonces, 驴por qu茅 no traducir el mecanismo de RL subyacente nuevamente en fen贸menos naturales que se pretende simular? La gente aprende mejor a trav茅s de las historias.
Esta es la historia del modelo Actor Advantage Critic (A2C). El modelo de sujeto cr铆tico es una forma popular del modelo Policy Gradient, que en s铆 mismo es un algoritmo RL tradicional. Si entiendes A2C, entiendes RL profundo.
Despu茅s de obtener una comprensi贸n intuitiva de A2C, verifique:
Ilustraciones @embermarke
En RL, el agente, el zorro Klyukovka, se mueve a trav茅s de estados rodeados de acciones, tratando de maximizar las recompensas en el camino.
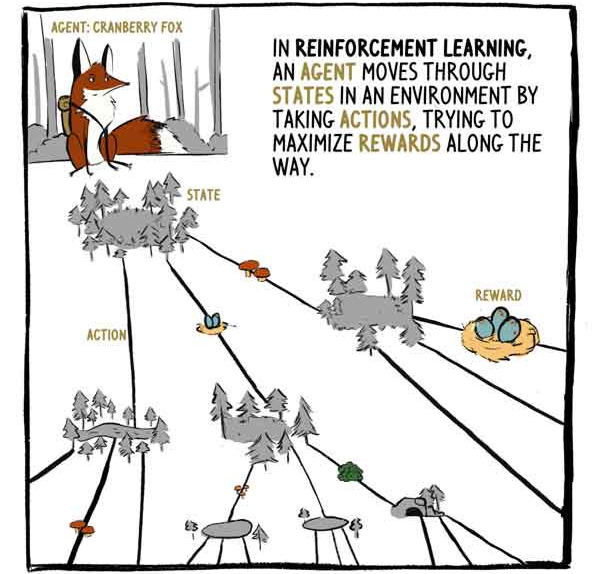
A2C recibe entradas de estado - entradas de sensor en el caso de Klukovka - y genera dos salidas:
1) Una evaluaci贸n de cu谩nta remuneraci贸n se recibir谩, a partir del momento del estado actual, con la excepci贸n de la remuneraci贸n actual (existente).
2) Una recomendaci贸n sobre qu茅 medidas tomar (pol铆tica).
Cr铆tico: wow, qu茅 maravilloso valle! 隆Ser谩 un d铆a fruct铆fero para buscar comida! Apuesto a que hoy recoger茅 20 puntos antes del atardecer.
"Sujeto": estas flores se ven hermosas, siento un antojo por "A".
Los modelos Deep RL son m谩quinas de mapeo de entrada-salida, como cualquier otro modelo de clasificaci贸n o regresi贸n. En lugar de categorizar im谩genes o texto, los modelos RL profundos traen estados a acciones y / o estados a valores de estado. A2C hace las dos cosas.
Este conjunto de recompensa de acci贸n estatal es una observaci贸n. Ella escribir谩 esta l铆nea de datos en su diario, pero todav铆a no va a pensar en ello. Ella lo llenar谩 cuando se detenga a pensar.
Algunos autores asocian la recompensa 1 con el tiempo paso 1, otros la asocian con el paso 2, pero todos tienen en cuenta el mismo concepto: la recompensa est谩 asociada con el estado y la acci贸n la precede inmediatamente.
Enganchar repite el proceso nuevamente. Primero, percibe su entorno y desarrolla una funci贸n V (S) y una recomendaci贸n para la acci贸n.
Cr铆tico: Este valle parece bastante est谩ndar. V (S) = 19.
Asunto: Las opciones de acci贸n son muy similares. Creo que simplemente ir茅 por la pista "C".
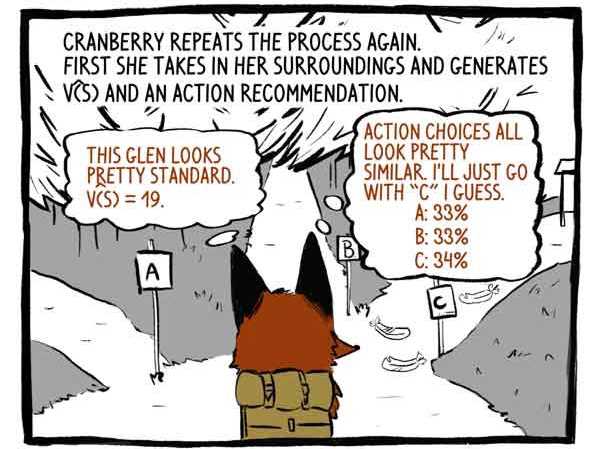
Entonces act煤a.
隆Recibe una recompensa de +20! Y registra la observaci贸n.
Ella repite el proceso nuevamente.
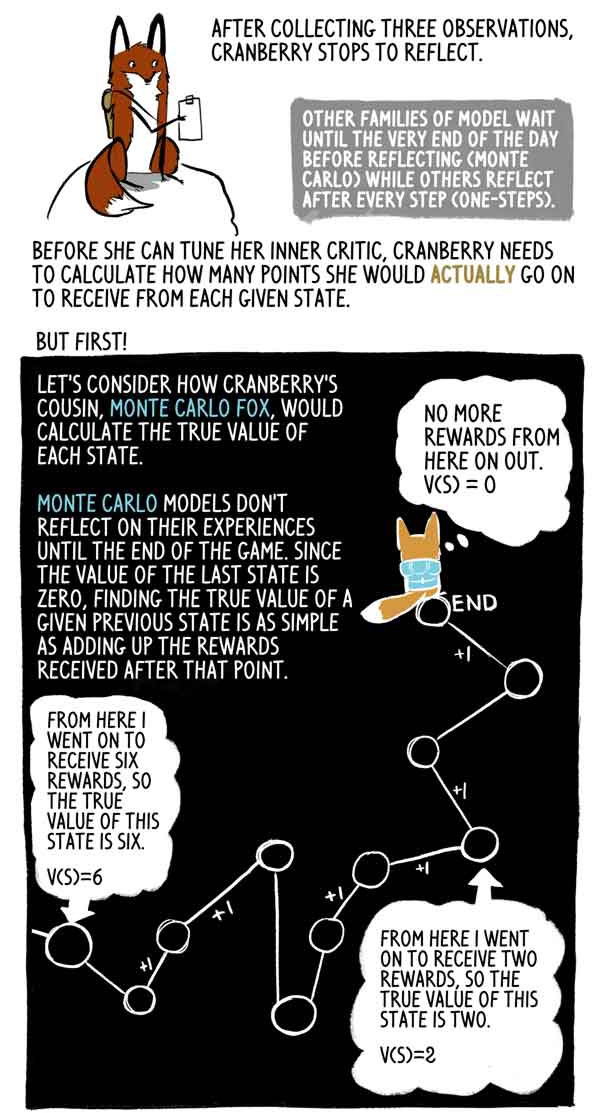
Despu茅s de recoger tres observaciones, Klyukovka se detiene a pensar.
Otras familias modelo esperan hasta el final del d铆a (Monte Carlo), mientras que otras piensan despu茅s de cada paso (un paso).
Antes de que pueda configurar su cr铆tico interno, Klukovka necesita calcular cu谩ntos puntos recibir谩 realmente en cada estado.
Pero primero!
Veamos c贸mo la prima de Klukovka, Lis Monte Carlo, calcula el verdadero significado de cada estado.
Los modelos de Monte Carlo no reflejan su experiencia hasta el final del juego, y dado que el valor del 煤ltimo estado es cero, es muy simple encontrar el verdadero valor de este estado anterior como la suma de las recompensas recibidas despu茅s de este momento.
De hecho, esta es solo una muestra de alta dispersi贸n V (S). El agente podr铆a seguir f谩cilmente una trayectoria diferente desde el mismo estado, recibiendo as铆 una recompensa agregada diferente.
Pero Klyukovka se va, se detiene y reflexiona muchas veces hasta que el d铆a llega a su fin. Ella quiere saber cu谩ntos puntos obtendr谩 realmente de cada estado hasta el final del juego, porque quedan varias horas hasta el final del juego.
Ah铆 es donde hace algo realmente inteligente: la zorra Klyukovka estima cu谩ntos puntos recibir谩 por el 煤ltimo estado en este set. Afortunadamente, tiene una evaluaci贸n correcta de su condici贸n: su cr铆tica.
Con esta evaluaci贸n, Klyukovka puede calcular los valores "correctos" de los estados anteriores exactamente como lo hace el zorro de Monte Carlo.
Lis Monte Carlo eval煤a las marcas de destino, realiza el despliegue de la trayectoria y agrega recompensas hacia adelante desde cada estado. A2C corta esta trayectoria y la reemplaza con una evaluaci贸n de su cr铆tico. Esta carga inicial reduce la varianza de la puntuaci贸n y permite que el A2C se ejecute continuamente, aunque introduciendo un peque帽o sesgo.
Las recompensas a menudo se reducen para reflejar el hecho de que la remuneraci贸n ahora es mejor que en el futuro. Por simplicidad, Klukovka no reduce sus recompensas.
Klukovka ahora puede pasar por cada fila de datos y comparar sus estimaciones de valores de estado con sus valores reales. Ella usa la diferencia entre estos n煤meros para perfeccionar sus habilidades de predicci贸n. Cada tres pasos durante el d铆a, Klyukovka recopila una valiosa experiencia que vale la pena considerar.
鈥淐alifiqu茅 mal los estados 1 y 2. 驴Qu茅 hice mal? Si! La pr贸xima vez que vea plumas como estas, aumentar茅 V (S).
Puede parecer una locura que Klukovka pueda usar su calificaci贸n V (S) como base para compararlo con otros pron贸sticos. 隆Pero los animales (incluidos nosotros) hacen esto todo el tiempo! Si siente que las cosas van bien, no necesita volver a capacitar las acciones que lo llevaron a este estado.
Al recortar nuestros resultados calculados y reemplazarlos con una estimaci贸n de carga inicial, reemplazamos la gran variaci贸n de Monte Carlo con un peque帽o sesgo. Los modelos RL suelen sufrir una alta dispersi贸n (que representa todos los caminos posibles), y tal reemplazo generalmente vale la pena.
Klukovka repite este proceso todo el d铆a, recogiendo tres observaciones de estado-acci贸n-recompensa y reflexionando sobre ellas.
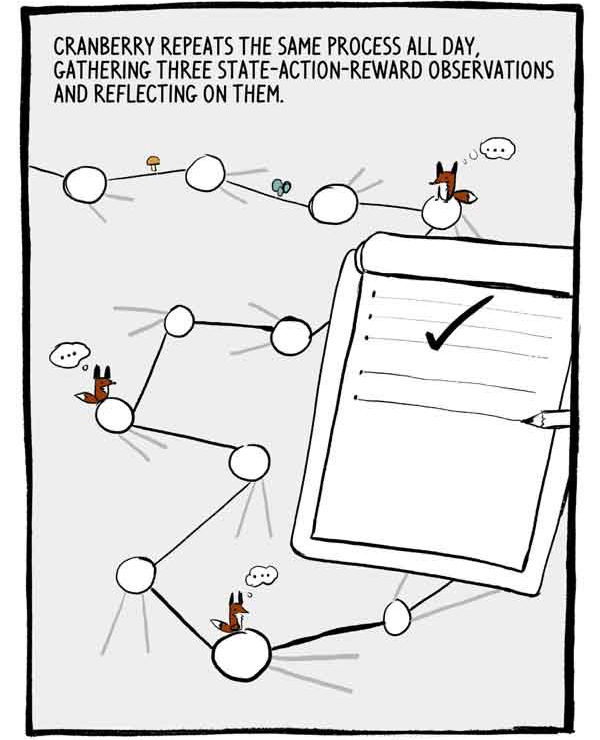
Cada conjunto de tres observaciones es una peque帽a serie autocorrelacionada de datos de entrenamiento etiquetados. Para reducir esta autocorrelaci贸n, muchas A2C capacitan a muchos agentes en paralelo, sumando su experiencia antes de enviarla a una red neuronal com煤n.
El d铆a finalmente est谩 llegando a su fin. Solo quedan dos pasos.
Como dijimos anteriormente, las recomendaciones de las acciones de Klukovka se expresan en porcentaje de confianza sobre sus capacidades. En lugar de simplemente elegir la opci贸n m谩s confiable, Klukovka elige de esta distribuci贸n de acciones. Esto asegura que ella no siempre acepta acciones seguras, pero potencialmente mediocres.
Podr铆a arrepentirme, pero ... A veces, explorando cosas desconocidas, puedes llegar a nuevos descubrimientos emocionantes ...
Para alentar a煤n m谩s la investigaci贸n, un valor llamado entrop铆a se resta de la funci贸n de p茅rdida. Entrop铆a significa el "alcance" de la distribuci贸n de acciones.
- 隆Parece que el juego ha valido la pena!
O no?
A veces, el agente se encuentra en un estado donde todas las acciones conducen a resultados negativos. A2C, sin embargo, hace frente a situaciones malas.
Cuando se puso el sol, Klyukovka reflexion贸 sobre el 煤ltimo conjunto de soluciones.
Hablamos sobre c贸mo Klyukovka configura su cr铆tico interno. Pero, 驴c贸mo afina su "sujeto" interior? 驴C贸mo aprende a tomar decisiones tan exquisitas?
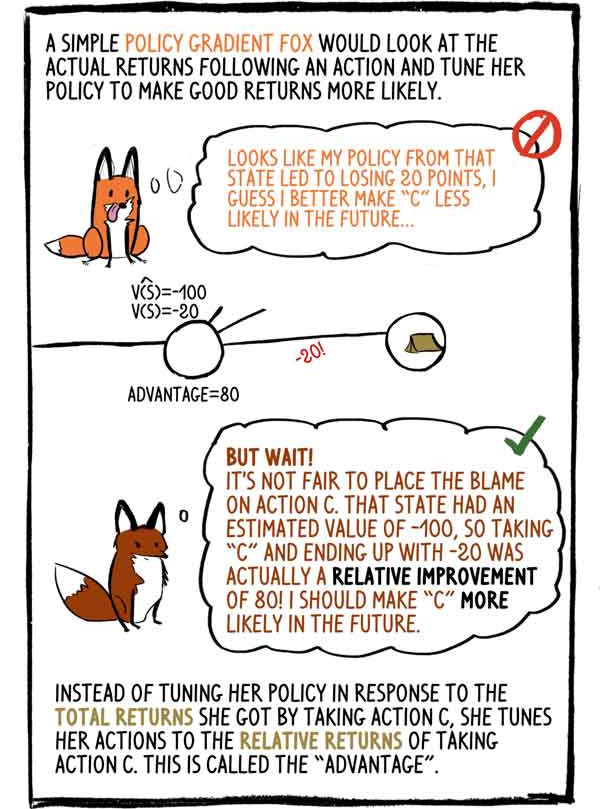
La pol铆tica de gradiente de zorro de mente simple mirar铆a los ingresos reales despu茅s de la acci贸n y ajustar铆a su pol铆tica para hacer que los buenos ingresos sean m谩s probables: - Parece que mi pol铆tica en este estado condujo a una p茅rdida de 20 puntos, creo que en el futuro es mejor hacer "C" menos probable
- Pero espera! Es injusto culpar a la acci贸n "C". Este estado ten铆a un valor estimado de -100, por lo que elegir "C" y terminar con -20 fue en realidad una mejora relativa de 80. Tengo que hacer que "C" sea m谩s probable en el futuro.
En lugar de ajustar su pol铆tica en respuesta a los ingresos totales que recibi贸 al seleccionar la acci贸n C, sintoniza su acci贸n con los ingresos relativos de la acci贸n C. Esto se denomina "ventaja".
Lo que llamamos una ventaja es simplemente un error. Como ventaja, Klukovka lo usa para hacer actividades que fueron sorprendentemente buenas, m谩s probables. Como error, ella usa la misma cantidad para presionar a su cr铆tico interno a mejorar su evaluaci贸n del valor del estado.
El sujeto aprovecha:
- "Wow, eso funcion贸 mejor de lo que pensaba, la acci贸n C debe ser una buena idea".
El cr铆tico usa el error:
鈥溌縋ero por qu茅 me sorprendi贸? Probablemente no deber铆a haber evaluado esta condici贸n tan negativamente ".
Ahora podemos mostrar c贸mo se calculan las p茅rdidas totales: minimizamos esta funci贸n para mejorar nuestro modelo.
"P茅rdida total = p茅rdida de acci贸n + p茅rdida de valor - entrop铆a"
Tenga en cuenta que para calcular los gradientes de tres tipos cualitativamente diferentes, tomamos los valores "a trav茅s de uno". Esto es efectivo, pero puede dificultar la convergencia.
Como todos los animales, a medida que Klyukovka crezca, perfeccionar谩 su capacidad de predecir los valores de los estados, ganar谩 m谩s confianza en sus acciones y, con menos frecuencia, se sorprender谩 de los premios.
Los agentes de RL, como Klukovka, no solo generan todos los datos necesarios, simplemente interact煤an con el entorno, sino que tambi茅n eval煤an las etiquetas de destino. As铆 es, los modelos RL actualizan las calificaciones anteriores para que coincidan mejor con las calificaciones nuevas y mejoradas.
Como dice el Dr. David Silver, jefe del grupo RL en Google Deepmind: AI = DL + RL. Cuando un agente como Klyukovka puede establecer su propia inteligencia, las posibilidades son infinitas ...
