🧗🏽 🕴🏻 🕝 Catálisis de muones en términos de química cuántica. Parte I: hidrógeno ordinario vs. muon hidrógeno 🎷 🔠 ❄️

Mnogabukaff que la química cuántica piensa en el principio de la catálisis de muones: cómo exactamente el muón reduce la temperatura del plasma deseado. En dos partes

La esencia de la primera parte se expresa en una oración: el muón es más pesado que el electrón, por lo que es más difícil separarlo del protón.

Pero aquellos que quieran ver las fórmulas, los gráficos y ver la esencia conceptual de la química cuántica aplicada a los átomos más simples (cuasi), bienvenidos bajo cat.

La segunda parte está disponible en este enlace .

Introduccion

No es ningún secreto que el consumo de energía por parte de la humanidad está creciendo cada año: cada uno de nosotros tiene más dispositivos, tenemos que movernos por allí, y nosotros mismos no somos menos. Por lo tanto, estamos constantemente en el pensamiento, dónde obtener más energía y dónde ahorrar esta energía.

Una de las posibles alternativas a las principales fuentes de energía actuales (carbón, gas, centrales hidroeléctricas y energía nuclear) es la fusión termonuclear (TS) . De hecho, este es el buen hermano gemelo de la energía nuclear malvada, lo ~~principal que no debemos recordar acerca de la Bomba Zar~~ : en lugar de las reacciones de fusión en el TS, la fusión de los núcleos de luz en los más pesados sirve como fuente de energía. Y todo parece estar bien: todas nuestras fuentes de energía aparecieron de alguna manera gracias al TS, porque fluye en las estrellas (incluso dentro del Sol) y sirve como fuente de luz y calor, debido a lo cual ocurren todas las reacciones de fotosíntesis, todas fluyen soplan ríos y vientos. Pero también gracias a TS, tenemos un montón de elementos más pesados que el helio (incluyendo carbono = carbón, petróleo, gas y uranio).
Las principales reacciones de síntesis putativas son las reacciones de fusión de diferentes isótopos de hidrógeno (protio

${} _ {1} ^ {1} \ mathrm {H}$ deuterio

${} _ {1} ^ {2} \ mathrm {H}$ y tritio

${} _ {1} ^ {3} \ mathrm {H}$ )El problema es que para arrancar el vehículo en un modo autosuficiente, necesita temperaturas increíblemente altas. No hay ningún problema con las estrellas, pero en condiciones terrestres, tal requisito sigue siendo un obstáculo para la corriente que fluye de una fusión termonuclear ecológica en cada salida.Una forma de bajar la temperatura es la catálisis de muones .Vicki nos dice que muon (

$\ mu ^ -$ ) Es un clon de electrones pesados tan inestable (

$e ^ -$ ): es 207 veces más pesado que un electrón y solo vive 2.2 microsegundos. Pero, se supone que la adición de tales partículas al sistema donde ocurre el TS, podrá reducir la temperatura mínima del plasma necesaria para la fusión de nuevos núcleos. Y dado que se pueden formar muones durante algunas de las reacciones de síntesis, en lugar de partículas en descomposición, deberían aparecer nuevas partículas que continuarán ~~participando en la alquimia para~~ quemar hidrógeno y otros elementos con la formación de otros más pesados.En las diferencias entre las formas habituales de hidrógeno y aquellas en las que el electrón se reemplaza por un muón y se cubre toda la esencia de la catálisis del muón. Y para ver esto, debemos recurrir a la química cuántica y sus conceptos, lo cual haremos.En esta parte, nos centraremos en las diferencias en el átomo de hidrógeno (

$\ mathrm {H ^ \ cdot = p ^ + e ^ -}$ ) de su homólogo muón (

$\ mathrm {p} ^ + \ mu ^ -$ ), en el que el electrón se reemplaza por un muón.

Volando sobre el nido del protón ...

Un par de palabras comunes

Átomo de hidrógeno Todos lo discuten y se lleva a cabo en la escuela en clases de física y química, por lo que discutiremos cómo reemplazar un electrón con un muón afectará sus propiedades (energía y tipo de orbitales).Consideramos estas partículas desde dos posiciones generales:

pervertido (la llamada mecánica cuántica antigua),
y desde el punto de vista del quantummech normal.

La primera consideración está disponible para los escolares, la segunda requerirá un conocimiento más profundo de las matemáticas superiores .

Órbitas de Bohr

De hecho, la antigua mecánica cuántica es un intento de adaptar la mecánica clásica para describir sistemas que no la obedecen. A pesar del hecho de que para una descripción completa, este enfoque es muy defectuoso (que discutiremos en la siguiente sección), es importante e interesante, y al mismo tiempo inusualmente simple.

En primer lugar, fue a través de la antigua mecánica cuántica que los físicos lograron detectar lo que estaba mal con los sistemas cuánticos, por lo tanto, desde un punto de vista histórico, este paso fue necesario e importante para cambiar el paradigma de la física.
En segundo lugar, la solución de Bohr al problema de un átomo de átomos similares al hidrógeno que consta de dos partículas cargadas positiva y negativamente podría explicar las observaciones experimentales y unir todo el zoológico de series observado en los espectros de hidrógeno. Una versión perjudicial de esta decisión, que le trajo a Bohr el Nobel de 1922, la consideraremos aquí.

Pero para resolver el problema, debemos recordar cómo describimos el movimiento de una partícula en el caso clásico. Este es un programa escolar de física, pero si alguien lo olvidó, puede actualizar su memoria aquí:

¿Cómo se describe el movimiento de partículas en la mecánica clásica?

Usualmente asociamos con una partícula un modelo de un punto material: una cosa sin estructura, en la cual podemos medir su posición (dejemos

$x$ ) y velocidad (

$v = \ frac {dx} {dt} = \ dot {x}$ , de " velocidad "), es decir cambio de posición con el paso del tiempo

$t$ .Y la esencia de la descripción del movimiento de tal punto es muy simple: si conocemos la posición / velocidad del punto en algún punto inicial en el tiempo

$t_0$ , podemos predecir dónde estará este punto en cualquier otro momento

$t$ , y también con qué velocidad se moverá en este momento. Además, somos tan omnipotentes que podemos mirar no solo hacia el futuro, sino también hacia el pasado: el momento

$t$ tal vez antes

$t_0$ (

$t <t_0$ ),La predicción en sí misma, de acuerdo con todas las leyes del género mágico, debe basarse en cierto hechizo, y es conocida por todos los ~~escolares~~ que estudian física. Esta es la segunda ley de Newton , que no es más que un fuerte chamanismo del tipo de ecuaciones diferenciales de segundo orden:

$F = ma \.$ Aquí, como de costumbre, a es la aceleración (de " aceleración "), la primera derivada de la velocidad (

$a = \ frac {d v} {dt}$ ), o el segundo para la coordenada (

$a = \ frac {d ^ 2 x} {dt ^ 2}$ , por lo tanto, el segundo orden).Pero además de la aceleración en esta brujería, tenemos otro milagro de judo, que es responsable de cómo se moverá la partícula: esta es la fuerza F. Ella, como todos recuerdan, describe algo que controla el movimiento de una partícula. Un tipo de fuerza especial, que incluye las dos interacciones fundamentales más familiares para todos ( gravitacionalmente desalmadas y electromagnéticas), es la llamada fuerzas potenciales En este caso, puede introducir otra entidad, llamada energía potencial (la denotaremos con la letra V ), que guiará las transformaciones de los diferentes sistemas.En la línea inferior, para predecir el movimiento de un punto material, necesitamos tener (además de sus características, como masa y carga):

velocidad inicial y posición
la ley que lo gobierna, dada en forma de una expresión para la fuerza F , o mejor aún, el potencial V , que dará fuerza a la segunda ley de Newton como $F (x) = - \ frac {dV} {dx} (x)$ .

Basado en estos datos, sustituyéndolo todo en la ecuación

$F = ma$ Recibiremos la trayectoria de la partícula: el valor de su posición y velocidad en cada momento en el tiempo.Eso es todo lo que necesitamos para describir el movimiento en el mundo que fácilmente observamos.

Pasemos a la tarea. Entonces, tenemos dos partículas con carga opuesta que se atraen entre sí de acuerdo con la ley de Coulomb, es decir, la energía potencial de atracción es

$V (R) = \ overbrace {\ frac {1} {4 \ pi \ varepsilon_0}} ^ {k} \ frac {q_1 q_2} {R} = k \ frac {q_1 q_2} {R}$ donde R es la distancia entre las partículas,

$q_i$ - cargas en el caso de un átomo de hidrógeno y una partícula

$\ mathrm {p} ^ + \ mu ^ -$ son iguales

$+ e \ aprox +1.6 \ veces 10 ^ {- 19}$ CL para protones y

$-e$ para electrones y muones, y

$\ varepsilon_0$ - constante eléctrica . Como las cargas son opuestas, la energía potencial disminuye al disminuir la distancia entre las partículas (es decir, durante la aproximación), lo que significa que el protón y el electrón / muón se atraen entre sí.

Esta situación se muestra en la imagen de arriba. Pero en algún lugar vimos un sistema similar, ¿verdad? En realidad, en uno de estos pares vivimos: el Sol + Tierra o Tierra + Luna, o Tierra + ISS: estas también son dos partículas que son atraídas por un potencial similar expresado por la ley de Newton:

$V (R) = -G \ frac {m_1 m_2} {R}$

donde G es la constante gravitacional, y

$m_i$ - masas

El protón es 1836 veces más pesado que el electrón, y dado que el muón es 207 veces más pesado que el electrón, el protón es casi 9 veces más pesado que el muón. En ambos casos, tenemos el sistema de "partícula pesada + partícula ligera", por lo que tomamos la aproximación en la que el electrón / muón gira alrededor de un protón. Por supuesto, la precisión de esta suposición en el caso de

$\ mathrm {p} ^ + \ mu ^ -$ será significativamente más bajo que para un átomo de hidrógeno, pero para ilustración es bastante adecuado. En los casos del Sol + Tierra, Tierra + ISS usualmente usan aproximaciones similares.

Estamos interesados en un sistema estable en el que nada cae en ninguna parte, porque Los átomos de hidrógeno, si no se tocan, existen durante mucho tiempo.

Conocemos tales movimientos en el caso de todos los análogos del sistema solar, y para el par Tierra + ISS son incluso obvios: estas son órbitas estables en las que la estación se mueve alrededor de la Tierra a una velocidad suficiente para no caer. Esta velocidad se llama la primera velocidad cósmica , es decir. necesitaríamos la primera velocidad cósmica para el átomo de hidrógeno / su contraparte de muón. Y es fácil encontrarlo por fórmulas escolares (ver la figura anterior).

Cuando se mueve en una órbita circular con radio R (en la figura se indica como

$a_0$ , y pronto llegamos a esto) debes tener velocidad

$v$ . Uno puede imaginar que en cada momento dos fuerzas que actúan sobre una partícula que vuela en un círculo son perpendiculares al vector de velocidad:

Fuerza de gravedad de Coulomb dirigida al centro, que, según la definición de fuerza $F = - \ frac {dV} {dR}$ es igual a
$F_ \ text {K} = -k \ frac {e ^ 2} {R ^ 2}$
la fuerza centrífuga (falsa) lo contrarresta, lo que intenta aumentar el radio de la órbita R , la expresión para ello tiene la forma
$F_ \ text {q} = \ frac {mv ^ 2} {R}$

donde m es la masa del electrón / muón (el satélite natural del protón).

La condición de que una partícula ligera no choque con una pesada es que la suma de estas fuerzas perpendiculares a la dirección de movimiento de la partícula debe ser cero (

$F_ \ mathrm {K} + F_ \ mathrm {q} = 0$ ), lo que significa que obtenemos la ecuación

$\ frac {mv ^ 2} {R} = k \ frac {e ^ 2} {R ^ 2}$

de donde obtenemos la velocidad con la que es necesario volar un electrón / muón con masa m en el radio de la órbita R , para no chocar contra el protón:

${v} = \ sqrt {k \ frac {e ^ 2} {mR}}$

Y todo se lastimaría si el electrón / muón no estuviera cargado, y las partículas cargadas emiten ondas electromagnéticas cuando se mueven en círculo (esto se llama fricción radiante) , lo que haría inestable dicho sistema: el electrón / muón emitiría luz durante la rotación, Como resultado, perdió energía y redujo el radio de su órbita, y finalmente cayó sobre un protón, y habría un pequeño animal blanco y esponjoso en todo. Pero, obviamente, esto no sucede, lo que significa que algo debería diferir radicalmente en el comportamiento de partículas tan pequeñas como el electrón / muón.

En realidad, Niels Bohr también propuso una hipótesis muy tonta (en ese momento). Admitió que hay órbitas con cierto radio, en las que el átomo de hidrógeno no emite nada. Y ahora la pregunta es cómo encontrar estas órbitas. Para simplificar, usaremos el logro más tarde de lo que estaba disponible para Bohr: la expresión para la longitud de onda de De Broglie :

$\ lambda = \ frac {h} {p} = \ frac {h} {mv}$

Antecedentes historicos

La fórmula de Broglie se obtuvo a principios de la década de 1920 (1923-1924), y Bohr describió el átomo de hidrógeno en 1913 .

Se supone que la materia (partículas) también tiene propiedades de onda, y se les puede atribuir una cierta longitud de onda, que es dada por la fórmula de De Broglie. Luego, para que el movimiento en un círculo sea estacionario en el tiempo (para ser una onda estacionaria), se requiere que la longitud de la órbita (

$L = 2 \ pi R$ ) se ajustan a un número entero de ondas.

Entonces, el movimiento ondulatorio del electrón / muón se puede representar de alguna manera ( tomado de Wiki ):
imagen

En el lenguaje de las fórmulas, esto se expresa como:

$2 \ pi R = n \ lambda = n \ frac {h} {mv}$

Sustituyendo aquí la primera velocidad del protón cósmico obtenida anteriormente, obtenemos la ecuación

$2 \ pi R = \ frac {nh} {m} \ sqrt {\ frac {mR} {ke ^ 2}}$ . Habiendo cuadrado ambos lados, obtenemos la expresión para el radio de la enésima órbita estacionaria de electrones / muones:

$R_n = n ^ 2 \ left (\ overbrace {\ frac {h} {2 \ pi}} ^ {\ hbar} \ right) ^ 2 \ cdot \ frac {1} {mk e ^ 2} = \ frac { n ^ 2 \ hbar ^ 2} {mk e ^ 2}$

Aqui

$n = 1,2,3, \ ldots$ (no tenemos un límite en el número de olas que se colocarán), y

$\ hbar$ - este es el llamado Reducción constante de Planck. Cuantas más ondas apilemos, mayor será el radio de la órbita. Con el radio mínimo ( n = 1) en el caso de un electrón (es decir, m es igual a la masa del electrón m _e ), dicho radio se llama radio de Bohr, como K.O. Fig. Arriba):

$a_0 = R_0 = \ frac {\ hbar ^ 2} {m_ \ mathrm {e} ke ^ 2}$

La sustitución de números ( ħ = 1.054 × 10 ^–34 J · s, m _e = 9.109 × 10 ^-31 kg, k = 8.99 × 10 ⁹ N · m ² · C ⁻² y e = −1.602 × 10 ⁻¹⁹ C) da el valor a ₀ = 5.29 × 10 ⁻¹¹ mo 0.529 angstroms (Å).

¿Cuánto cuesta Angstrom?

1 Å = 10 ⁻¹⁰ m. Esto es muy pequeño.

En el curso de los cálculos, de paso introdujimos una nueva entidad: el número

$n = 1,2,3, \ ldots$ que determina el número de ondas y

$\ Rightarrow$ el radio de la órbita, e incluso la velocidad del electrón en órbita. Este número es conocido por todos desde la escuela: este es el número cuántico más importante de un átomo similar al hidrógeno. Hablaremos de esto con más detalle en la siguiente sección, pero por ahora puedes intentar encontrar la energía de cada uno de los niveles.

Según lo entendemos, la energía de un sistema cerrado (y no hay duda de que nuestro átomo similar al hidrógeno es tal) consta de dos partes:

de energía cinética $T = \ frac {mv ^ 2} {2}$ ,
y potencial, que en nuestro caso está dado por la ley de Coulomb $V = \ frac {ke ^ 2} {R}$ .

Sustituimos la velocidad y el radio de la órbita en ellos por el número principal elegido n . Ya hemos escrito el radio, pero la velocidad se verá como

$v_n ^ 2 = \ frac {k e ^ 2} {m R_n} = \ frac {k ^ 2 e ^ 4} {n ^ 2 \ hbar ^ 2}$ .

Entonces

$T_n = \ frac {m v_n ^ 2} {2} = \ frac {m} {2} = \ frac {m k ^ 2 e ^ 4} {2 n ^ 2 \ hbar ^ 2}$ . Con potencial, todo es más simple:

$V_n = - \ frac {ke ^ 2} {R_n} = - \ frac {m k ^ 2 e ^ 4} {n ^ 2 \ hbar ^ 2}$ . Resumiendo estas contribuciones, obtenemos la energía total de un átomo similar al hidrógeno:

$E_n = T_n + V_n = - \ frac {m k ^ 2 e ^ 4} {2 n ^ 2 \ hbar ^ 2}$

Y esta fórmula jugó un papel importante en demostrar la corrección de la mecánica cuántica, ya que se observaron montones de líneas espectrales (Lyman, Balmer, Paschen, etc.) en los espectros del átomo de hidrógeno. Y con una fórmula y un modelo simple, todos lograron explicarse a la vez, lo cual fue un argumento increíblemente convincente a favor de reconocer las ideas de Bohr.

Habiendo exprimido todos los jugos de este modelo más simple, podemos proceder a la consideración correcta del problema desde el punto de vista de la mecánica cuántica honesta.

Orbitales de un átomo similar al hidrógeno

La segunda, aún más importante, es qué es la mecánica cuántica y cómo funciona. Esto se puede recordar de varias fuentes. Yo recomiendo:

para no ir muy lejos, un artículo de Habr: Libro “Mecánica cuántica. Mínimo teórico " (una pieza del libro del mismo nombre de Leonard Sasskind y Art Friedman ),
impresionante libro "Cómo entender la mecánica cuántica" del maestro de MFTIshnogo MG Ivanova (disponible para descargar desde el enlace),
en el foro dxdy en el Elegido, hay muchas publicaciones que explican bien la esencia de la cuantización ,
reseña bastante adecuada y artículo histórico sobre Lurke ,
Bueno, toda la basura también se encuentra en Internet.
Manual de red sobre química cuántica de VK .

Sin embargo, también hay un apretón de las cosas necesarias aquí:

¿Cómo se describe el movimiento de partículas en la mecánica cuántica?

En mecánica cuántica, el movimiento de una partícula (representada como un punto material, es decir, basura pequeña sin estructura) no puede describirse utilizando una trayectoria. Esto prohíbe el muy famoso principio de incertidumbre de Heisenberg :

$\ Delta x \ cdot \ Delta p \ geq \ frac {\ hbar} {2}$

donde

$\ Delta x$ Es el error al medir las coordenadas de las partículas, y

$\ Delta p$ - el error al medir el momento de la partícula, que se asocia con la velocidad como

$p = mv$ . De hecho, esta desigualdad dice: si mides la posición de la partícula con mucha precisión (el error

$\ Delta x$ pequeño), entonces el tablero para esto será un gran error al medir el momento de las partículas

$\ Delta p$ (y, por lo tanto, velocidad), y viceversa. Y la barra inferior de dicha precisión conjunta se expresa en términos de la constante de Planck reducida ħ = 1.054571800 (13) × 10 ⁻³⁴ J · s , que está relacionada con la constante de Planck habitual h como

$h = 2 \ pi \ hbar$ . Como puede ver, este valor es muy pequeño, por lo tanto, en nuestro mundo, en el límite de precisión de medición de nuestros instrumentos convencionales (velocímetros, reglas, etc.), no sentimos este límite inferior de esta desigualdad, por lo que nos parece que todo se puede medir con cualquier precisión
Pero para partículas pequeñas y ligeras, como un electrón y un muón, no importa cuánto lo intentemos, es imposible en cualquier momento descubrir dónde y a qué velocidad vuela esta mierda.

De hecho ...

Hay versiones (formalismos) de la mecánica cuántica, donde de una forma u otra hay trayectorias. Los ejemplos más obvios son:

La técnica de las integrales a lo largo de las trayectorias de Richard Feynman , en la que cada partícula, cuando se mueve del punto "A" al punto "B", pasa (en diversos grados) a lo largo de todas las trayectorias posibles e imposibles,
La interpretación de la onda piloto de De Broglie-Bohm , en la que cada partícula se mueve, como en la mecánica clásica, a lo largo de un solo camino, aunque este camino es guiado, además de las fuerzas ordinarias, por los llamados fuerza cuántica que surge de la función de onda de una partícula.

Naturalmente, en ambos casos, todos los resultados y conclusiones son exactamente los mismos que en la mecánica cuántica de ondas estándar, de la que hablaremos ahora. En particular, el principio de incertidumbre de Heisenberg no desaparece en ninguna parte, simplemente adquiere una semántica diferente.
Se puede encontrar un poco más sobre estas versiones de la mecánica cuántica en el libro de M. G. Ivanov, "Cómo entender la mecánica cuántica" .

Por lo tanto, para describir el movimiento de los objetos cuánticos, se requirió un nuevo lenguaje y una nueva perspectiva de las cosas, y después de mucho tormento y montones de intentos de diversos grados de éxito, en 1926 por Erwin Schrödinger

(cuya vida personal era muuuy interesante)

Schrödinger tuvo una sola esposa toda su vida, lo que no le impidió tener un montón de amantes. En particular, obtuvo su famosa ecuación en los Alpes de vacaciones con un amante joven (y posiblemente menor de edad).

Se derivó su famosa ecuación que describe la dinámica de cualquier sistema cuántico :

$i \ hbar \ frac {\ partial \ psi} {\ partial t} = \ hat {H} \ psi$

En lugar de trayectorias de partículas, tenemos una nueva entidad: la función de onda

$\ psi$ , una función compleja (en el caso general) que depende solo de las coordenadas de la partícula y el tiempo.

Lo cual, sin embargo, no es necesario.

La función de onda puede depender tanto de las coordenadas de la partícula.

$\ psi (x)$ (esta versión se llama representación de coordenadas ), y de impulsos

$\ psi (p)$ , esta forma se llama representación de impulso . Cualquiera de las ideas que elija, reflejan exactamente el mismo estado. La transición de una representación a otra se lleva a cabo a través de la transformada de Fourier.

La esencia de la mecánica cuántica reside en esta esencia: en lugar de predecir con precisión la posición / velocidad / de cualquier otra cantidad física de una partícula, solo podemos determinar con precisión la probabilidad de un resultado de medición en particular, y nada más. Los resultados de la medición en sí serán aleatorios, pero si tomamos una gran cantidad de sistemas idénticos y hacemos un montón de mediciones de una cierta cantidad física, entonces el resultado estadístico será consistente con nuestra predicción, pero no de resultados de medición específicos, como en la física clásica, sino de las probabilidades de diferentes mediciones.

En particular, la probabilidad de encontrar una partícula a la vez

$t$ en el rango

$x \ in [x_0, x_0 + \ delta x]$ será aproximadamente igual

$\ psi ^ * (x_0, t) \ cdot \ psi (x_0, t) \ cdot \ delta x = | \ psi (x_0, t) | ^ 2 \ cdot \ delta x$ donde "*" significa conjugación compleja.
En otras palabras, la cantidad

$| \ psi | ^ 2$ (el cuadrado del módulo de la función de onda) es la densidad de probabilidad de la distribución de las posiciones de la partícula, es decir, en términos generales, la "mancha" de la partícula en el espacio. Naturalmente, de este significado se deduce que

$\ int \ limits _ {- \ infty} ^ {+ \ infty} | \ psi (x) | ^ 2 dx = 1$ , ya que la probabilidad total de encontrar una partícula al menos en algún lugar debe ser igual a 1.

Pero todo es tan simple solo para la posición de la partícula. En el caso general, todas las cantidades medibles físicamente se expresan en forma de piezas especiales: operadores. Estos operadores están indicados por una tapa en la parte superior, es decir si tuviéramos algún valor clásico

$A$ , entonces su análogo cuántico será el operador

$\ hat {A}$ .

De hecho, el operador es un conjunto de algunas transformaciones que deben hacerse con la función de onda, y se escribe como

$\ hat {A} \ psi$ .

Por ejemplo:

operador coordinado $x$ es $\ hat {x} = x$ , por lo tanto, la acción de este operador en ψ es simplemente la multiplicación por el valor de la coordenada misma, es decir $\ hat {x} \ psi (x) = x \ psi (x)$ ,
operador de pulso $p$ es $\ hat {p} = - i \ hbar \ frac {d} {dx}$ , por lo tanto, cuando actúa sobre la función de onda, el resultado será la derivada de la función de onda ( $\ hat {p} \ psi (x) = -i \ hbar \ frac {d \ psi (x)} {dx} = -i \ hbar \ psi '(x)$ )

Todas las demás cantidades físicas se expresan de una forma u otra a través de momentos y coordenadas (

${A} = A (x, p)$ ), y sus operadores se obtienen sustituyendo

$\ hat {x}, \ hat {p}$ en expresiones clásicas (

$\ hat {A} = A (\ hat {x}, \ hat {p})$ )
Y el valor promedio de la cantidad física A especificada por el operador

$\ hat {A}$ si el sistema está en el estado descrito por la función de onda

$\ psi (x)$ calculado como

$\ int \ limits _ {- \ infty} ^ {+ \ infty} \ psi ^ * (x) \ hat {A} \ psi (x) dx$ . Por lo general, esta integral se escribe en notación de Dirac :

$\ langle \ psi | \ hat {A} | \ psi \ rangle = \ int \ limits _ {- \ infty} ^ {+ \ infty} \ psi ^ * (x) \ hat {A} \ psi (x) dx$

Un lector atento notó que en la ecuación de Schrödinger ya había un artilugio con tapa,

$\ hat {H}$ . Este es el operador de energía del sistema, que se llama el operador de Hamilton, o simplemente el hamiltoniano. Como ya se mencionó, la energía de una partícula es la suma de su energía cinética T y energía potencial V. Entonces el operador de energía también se ve así:

$\ hat {H} = \ hat {T} + \ hat {V}$

Por lo general, el potencial es simplemente una función de las coordenadas (

$V = V (x)$ ) y su forma específica depende de la tarea, pero ya sabemos cómo es la energía cinética clásica:

$T = \ frac {m v ^ 2} {2} = \ frac {p ^ 2} {2m}$ , lo que significa que el operador de energía cinética se parece a

$\ hat {T} = \ frac {\ hat {p} ^ 2} {2m} = - \ frac {\ hbar ^ 2} {2m} \ frac {d ^ 2} {dx ^ 2}$

.
En consecuencia, la ecuación de Schrödinger para una partícula se escribe como

$i \ hbar \ frac {\ partial \ psi} {\ partial t} = \ underbrace {(\ hat {T} + \ hat {V})} _ {\ hat {H}} \ psi = - \ frac { \ hbar ^ 2} {2m} \ frac {\ partial ^ 2 \ psi} {d \ partial ^ 2} + V (x) \ psi$
Esto no es más que una ecuación diferencial parcial de segundo orden, y en apariencia es una ecuación de calor con un coeficiente complejo de difusión de calor.

En muchos casos, estamos interesados en el problema de los estados estacionarios de un sistema, cuando nada actúa sobre él y existe esféricamente en vacío absoluto y en el ~~nirvana~~ . En tales casos, la ecuación de Schrödinger que contiene el tiempo se simplifica y solo podemos resolver una ecuación más simple:

$\ hat {H} \ psi (x) = E \ psi (x)$

que se llama la ecuación de Schrödinger estacionaria. Su solución es una función de onda.

$\ psi (x)$ describiendo el estado estacionario y la energía de este estado ( E ).

Para encontrar cómo se mueve un electrón / muón en un campo eléctrico de Coulomb creado por un protón, uno debe resolver la ecuación básica de la mecánica cuántica: la ecuación de Schrödinger. Dado que el sistema en consideración es estacionario (no cambia con el tiempo), es suficiente resolver su versión simplificada: la ecuación de Schrödinger estacionaria, que tiene la forma

$\ underbrace {(\ overbrace {- \ frac {\ hbar ^ 2} {2m} \ cdot \ left (\ frac {\ partial ^ 2} {\ partial x ^ 2} + \ frac {\ partial ^ 2} { \ partial y ^ 2} + \ frac {\ partial ^ 2} {\ partial z ^ 2} \ right)} ^ {\ hat {T}} + \ overbrace {- \ frac {ke ^ 2} {R}} ^ {\ hat {V}})} _ {\ hat {H}} \ psi = E \ psi$

Esta ecuación es una ecuación diferencial parcial de segundo orden, y en ella buscamos simultáneamente la función de onda

$\ psi (x, y, z)$ describiendo el estado específico del sistema y mostrando la "mancha" de la partícula negativa en el espacio alrededor del protón, y la energía de este estado E. La brujería que decide que se puede encontrar más o menos en todas partes .

¿Cómo se ve la función de onda?

$\ psi_ {nlm} (r, \ theta, \ varphi) = \ frac {1} {\ sqrt {2n {\ cdot} (n-l-1)! {\ cdot} (n + l)!}} {\ cdot} {\ left (\ frac {2} {n a_0} \ right)} ^ {\ frac32} {\ cdot} \ exp {\ left ({- \ frac {r} {n a_0}} \ right)} {\ cdot} {\ left (\ frac {2r} {n a_0} \ right)} ^ {l} L_ {nl-1} ^ {2l + 1 } {\ left (\ frac {2r} {n a_0} \ right)} \ cdot Y_ {l, m} (\ theta, \ varphi)$

(copiado de Wiki ). La solución se expresa en coordenadas esféricas .

Pero una cosa más simple: cualquier persona familiarizada con las ecuaciones diferenciales puede encontrar una solución para el estado fundamental de un átomo similar al hidrógeno. Para no asustar a todos los demás, esta pieza se elimina en el spoiler:

¿Cómo encontrar el orbital 1s y su energía?

Entonces, tenemos la ecuación de Schrödinger en coordenadas cartesianas

$(x, y, z)$ . Pero más natural en el caso de un átomo / partícula de hidrógeno

$\ mathrm {p} ^ + \ mu ^ -$ Se ve en coordenadas esféricas. Coloque el protón en el origen de las coordenadas cartesianas, y luego el cartesiano se expresará de forma esférica como

$\ begin {cases} x = R \ cdot \ cos (\ varphi) \ cdot \ sin (\ theta), \\ y = R \ cdot \ sin (\ varphi) \ cdot \ sin (\ theta), \\ z = R \ cdot \ cos (\ theta) \. \ end {cases}$

Aquí R es la distancia al protón (el mismo que está en la ley de Coulomb), y

$(\ varphi, \ theta)$ ángulos esféricos donde

$\ varphi$ - ángulo polar en el plano

$x0y$ y

$\ theta$ - el ángulo de salida de la partícula desde este plano:

imagen

Naturalmente, la pieza con las segundas derivadas parciales también corresponde en nuevas coordenadas:

$\ frac {\ partial ^ 2 \ psi} {\ partial x ^ 2} + \ frac {\ partial ^ 2 \ psi} {\ partial y ^ 2} + \ frac {\ partial ^ 2 \ psi} {\ partial z ^ 2} = \ left (\ frac {\ partial ^ 2 \ psi} {\ partial R ^ 2} + \ frac {2} {R} \ frac {\ partial \ psi} {\ partial R} \ right) + \ underbrace {{1 \ over R ^ 2 \ sin \ theta} {\ partial \ over \ partial \ theta} \ left (\ sin \ theta \ frac {\ partial} {\ partial \ theta} \ right) \ psi + \ frac {1} {R ^ 2 \ sin ^ 2 \ theta} \ frac {\ partial ^ 2} {\ partial \ varphi ^ 2} \ psi} _ {\ text {si hay una dependencia angular}}$

Parece que hemos complicado nuestras vidas, pero esto no es del todo cierto. Suponga que la función de onda

$\ psi$ es el mismo en todas las direcciones desde el protón (es decir, a una distancia fija del centro, se extiende uniformemente sobre la esfera de este radio), entonces nuestra función de onda no depende de los ángulos

$(\ varphi, \ theta)$ , y eso significa una parte grande y terrible de las segundas derivadas, simplemente desaparece con nosotros.

Como resultado, nos queda una ecuación para una coordenada:

$- \ frac {\ hbar ^ 2} {2m} \ left (\ frac {\ partial ^ 2 \ psi} {\ partial R ^ 2} + \ frac {2} {R} \ frac {\ partial \ psi} {\ parcial R} \ derecha) - \ frac {ke ^ 2} {R} \ psi = E \ psi$

Y ya no da tanto miedo, sin embargo, cómo resolver una ecuación de este tipo todavía no está muy claro.

Por lo tanto, utilizaremos un truco sucio: observe esta ecuación en la vecindad inmediata del protón (en

$R \ rightarrow 0$ ) En este caso, 2 piezas que contienen

$\ frac {1} {R}$ se disparan a valores tremendos, y los 2 miembros restantes caen muertos y siguen siendo pequeños.

¿No comieron una protuberancia?

no pueden crecer, de lo contrario se violará la condición

$\ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} | \ psi | ^ 2 dx dy dz = 1$ , que la partícula definitivamente se puede encontrar en algún lugar, porque esta integral se volverá infinita y esto no arreglará nada.

Como resultado, podemos resolver la ecuación simplificada solo para estas piezas grandes:

$- \ frac {\ hbar ^ 2} {2m} \ frac {2} {R} \ frac {\ partial \ psi} {\ partial R} - \ frac {ke ^ 2} {R} \ psi = 0$

Multiplicándolo por

$R$ y empujando los términos en diferentes lados de la igualdad, obtenemos la diferencia estándar de primer orden:

$\ frac {d \ psi} {d R} = - \ frac {mke ^ 2} {\ hbar ^ 2} \ psi$

Y resolverlo es simple:

$\ frac {d \ psi} {\ psi} = - \ frac {mke ^ 2} {\ hbar ^ 2} dR \ Rightarrow \ int _ {\ psi_0 = \ psi (R = 0)} ^ {\ psi (R )} \ frac {d \ psi} {\ psi} = - \ frac {mke ^ 2} {\ hbar ^ 2} \ int_ {0} ^ {R} dR \ Rightarrow \ ln \ left (\ frac {\ psi (R)} {\ psi_0} \ right) = - \ frac {mke ^ 2} {\ hbar ^ 2} R$

En otras palabras, la función de onda tiene la forma:

$\ psi (R) = \ psi_0 \ cdot \ exp \ left (- \ underbrace {\ frac {mke ^ 2} {\ hbar ^ 2}} _ {1 / R_1} R \ right) = \ psi_0 \ cdot \ exp \ left (- \ frac {R} {R_1} \ right)$
donde

$\ psi_0$ es solo una especie de coeficiente, pero

$R_1 = \ frac {\ hbar ^ 2} {mke ^ 2}$ Es el radio de la órbita de Bohr en

$n = 1$ (ver sección anterior). Inesperadamente, la vieja solución apareció nuevamente en la mecánica cuántica honesta.

Queda por verificar si la función de onda obtenida es una solución de la ecuación de Schrödinger en todas partes, y no solo cerca del protón. Para hacer esto, sustituimos la solución resultante en la ecuación original, para esto es conveniente encontrar la segunda derivada con respecto a R por adelantado:

$\ frac {d ^ 2 \ psi (R)} {dR ^ 2} = \ frac {d} {dR} \ underbrace {\ psi_0 \ exp \ left (- \ frac {R} {R_1} \ right)} _ {\ psi (R)} \ cdot \ left (- \ frac {1} {R_1} \ right) = \ frac {\ psi (R)} {R_1 ^ 2} = \ frac {m ^ 2k ^ 2e ^ 4} {\ hbar ^ 4} \ cdot \ psi (R)$

El resultado de la sustitución es:

$\ underbrace {\ frac {mk ^ 2 e ^ 4} {2 \ hbar ^ 2} \ psi (R)} _ {- \ frac {\ hbar ^ 2} {2m} \ frac {\ partial ^ 2 \ psi (R)} {\ parcial R ^ 2}} + \ underbrace {(- \ frac {\ hbar ^ 2} {2m} \ frac {2} {R} \ frac {\ partial \ psi (R)} {\ parcial R} - \ frac {ke ^ 2} {R} \ psi (R))} _ {0 \ \ text {(ya lo decidimos)}} = E \ psi (R)$

es decir

$\ frac {m k ^ 2 e ^ 4} {2 \ hbar ^ 2} \ psi (R) = E \ psi (R)$ , la solución sigue siendo la solución. Y cortando

$\ psi (R)$ en los lados izquierdo y derecho obtenemos:

$E = - \ frac {m k ^ 2 e ^ 4} {2 \ hbar ^ 2}$ , que es igual a la energía de la órbita de Bohr con

$n = 1$ .

El resultado de resolver la ecuación de Schrödinger es un conjunto de orbitales, que se describe utilizando tres enteros n , l y m , llamados "números cuánticos". La dependencia de las energías de estos orbitales en

$(n, l, m)$ a continuación (y steren de un recurso genial en química ):

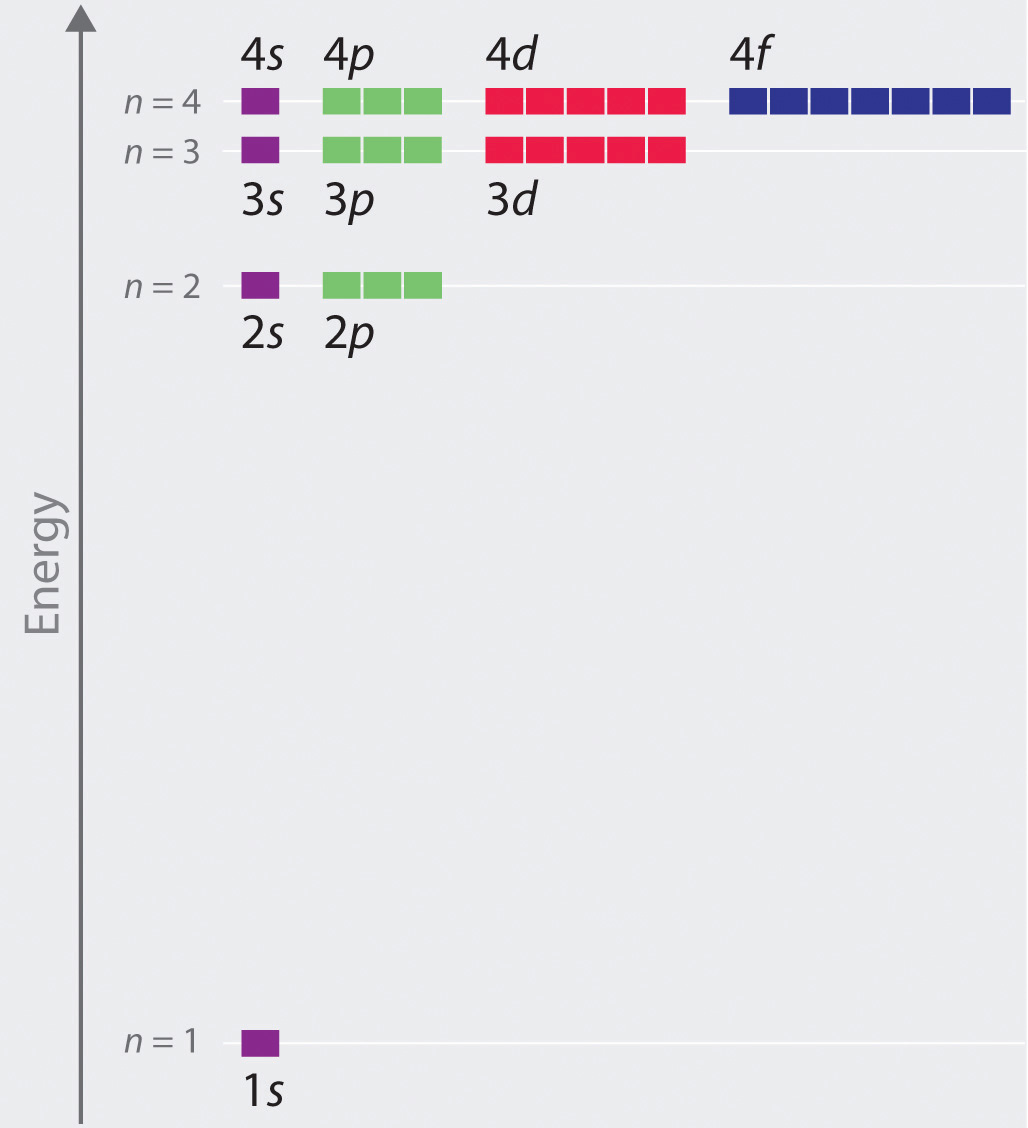
Con el primer número, n = 1,2,3, ... ya nos hemos encontrado. Este es el llamado Número cuántico principal. Determina la energía del nivel, así como el tamaño de la órbita de Bohr. (.. ) «». , / , , — , , , . n =1 n =2 ( ):

: , n . , .
l , , . n , n ( l=0,1,2,…,n ). , . , , . , ( ψ=0 ), , . - ( ):

«» . , .
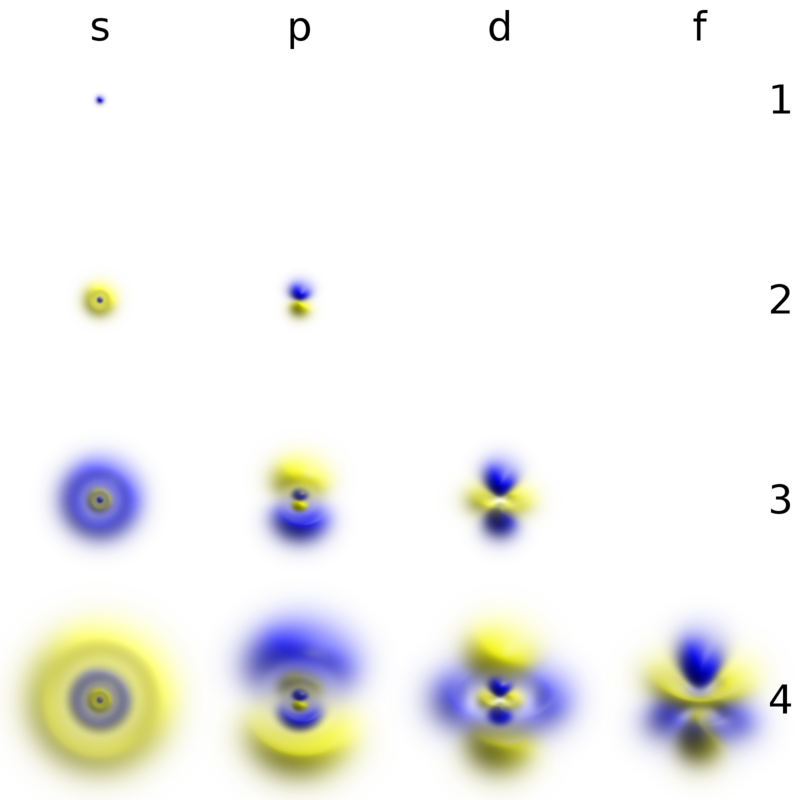
- $l=0$ , , , . s-.
- ( $l=1$ ) p-.
- 4- $l=2$ , d-. .
- 6- ( $l=3$ ) f-.
- 8- ( $l=4$ ) g-.
- 10- ( $l=5$ ) h-.
- .. etc.
, ( n ) , . : , .
, m , . . 2l+1 : $m = -l, -l+1, \ldots, 0 , \ldots , l-1, l$ .

Lo que obtuvimos como resultado: las energías en el caso cuántico resultaron ser las mismas que las de Bohr, pero el número de estados posibles para un n dado también resultó ser un número finito. Y este número crece con el aumento de la energía orbital. Inesperadamente, pero de acuerdo con los experimentos.

Entonces, ¿cuál es la diferencia entre un átomo de hidrógeno ( ) de su homólogo muón ( $\mathrm{H}^\cdot = \mathrm{p^+ e^-}$ )? $\mathrm{p}^+ \mu^-$

Ahora aplicamos las fórmulas obtenidas para comprender qué cambia exactamente cuando un electrón es reemplazado por un muón en un átomo de hidrógeno.

La energía del estado fundamental (es decir, el mínimo en energía, el más estable, desde dónde no ir), con el número cuántico principal n = 1. Está dado por la fórmula
$E_1 = - \frac{m k^2 e^4}{2 \underbrace{n^2}_{1^2} \hbar^2} = - \frac{m k^2 e^4}{2 \hbar^2}$

Cuando un electrón se transfiere a un muón, solo la masa ( $m_{\mu} \approx 207 m_\mathrm{e}$ , — , — ). , 207 : $E_1(\mathrm{p}^+\mu^-) = 207 E_1(\mathrm{H}^\cdot)$
. //, . $\mathrm{A \rightarrow A^+ + e^-}$ , A — . , $\mathrm{A \rightarrow A^+ + \mu^-}$ . . $E=0$ . $E_n = - \frac{m k^2 e^4}{2{n^2}\hbar^2}$ $n \rightarrow + \infty$ . Es decir , , / , , - (. ).

, ( $E>0$ , ).

, (IP) +/ :
$\mathrm{IP} = \underbrace{0}_{\text{ }} - \underbrace{E_1}_{\text{ }} = -E_1$

, + 207 , , .. «» , .
, «». , , (1s-)
$\psi_{1s}(R) = c\cdot \exp\left(-\frac{R}{R_1} \right)$

$R_1 = \frac{\overbrace{n^2}^{1^2} \hbar^2 }{mk e^2} = \frac{ \hbar^2 }{mk e^2}$ , cuanto más rápido disminuye la función de onda con la distancia desde el protón, y menor es su "tamaño", es decir localización de una partícula cargada negativamente. Al pasar de un electrón a un muón, este radio R ₁ disminuye en un factor de 207; por lo tanto, resulta que el muón está más unido al protón que el electrón. Y por lo tanto, es más difícil arrancarlo, ya que la ionización es esencialmente una transición a una órbita infinitamente distante, es decir. El muón necesita ir más allá del electrón para escapar del protón.

Conceptualmente, todas nuestras conclusiones de las fórmulas son infinitamente simples: resolver el problema para

$\ mathrm {H ^ \ cdot}$ y

$\ mathrm {p} ^ + \ mu ^ -$ tiene el mismo aspecto, pero debido al hecho de que el muón es más pesado, se adhiere más al protón y le resulta más difícil escapar de él.

Obviamente, ¿verdad? Pero con las fórmulas es aún más obvio.

¿Qué pasará después?

Este texto fue solo una preparación para la siguiente parte.

En él, discutiremos directamente el mecanismo propuesto para reducir la temperatura mínima de fusión.

PS sistema atómico de unidades

Finalmente, discutimos algo que nos simplificaría enormemente todas las fórmulas escritas anteriormente. En diferentes tareas (incluso escolares), la elección de unidades de medida puede facilitar enormemente la vida. Y en el caso de la mecánica cuántica, también hay un sistema de unidades muy conveniente. Este es el llamado Sistema atómico de unidades . Pertenece a la clase de unidades naturales, que es esencialmente lo contrario de las unidades antropocéntricas ( SI , GHS ), en las que las cantidades que una persona puede imaginar de inmediato se utilizan como piezas de referencia. Por ejemplo, en SI, la unidad de longitud es un metro (aproximadamente la longitud de un brazo / pierna de un adulto), masa - un kilogramo (aproximadamente la masa de cerveza en un círculo en el Oktoberfest), todo esto lo observamos en la vida cotidiana.

Los sistemas naturales de unidades, sin embargo, toman como base algo que simplifica las fórmulas en el campo de conocimiento correspondiente. Y en el caso de las unidades atómicas:

en primer lugar, se supone que la constante de Planck en todas partes es la unidad ( $\ hbar = 1$ ),
unidad de masa es la masa del electrón $m_ \ mathrm {e} \ aprox 9.1 \ veces 10 ^ {- 31}$ kg
la unidad de carga es la carga de protones (o, equivalentemente, el módulo de carga de electrones) $e = 1.6 \ veces 10 ^ {- 19}$ Kl
Bueno, al mismo tiempo, la constante eléctrica se toma como la unidad. $k = \ frac {1} {4 \ pi \ varepsilon_0}$ , por lo que la ley de Coulomb toma la forma $V (R) = \ frac {q_1 q_2} {R}$ .

En este caso, el radio de Bohr del estado fundamental para el átomo de hidrógeno se convierte en la unidad de longitud

$a_0 = R_1 = \ frac {\ hbar ^ 2} {m_ \ mathrm {e} k e ^ 2} = 1$ (como recordamos, esto es aproximadamente 0.5 Å). La unidad de energía se convierte en un valor llamado Hartree (en honor al ángulo D de Hartree ), que se denota

$E_ \ mathrm {h} = \ frac {m_ \ mathrm {e} k ^ 2 e ^ 4} {\ hbar ^ 2} = 1$ . Se ve que la energía del nivel 1 de hidrógeno en unidades atómicas es 0.5 Hartree.

En la siguiente parte estaremos activamente sentados en estas unidades.

Hecho divertido

Las unidades de masa atómica (amu) son familiares para todos, desde las clases de química de la escuela. Estos son los que figuran en la tabla periódica (1/12 de la masa del isótopo de carbono principal

${} ^ {12} \ mathrm {C}$ ) ¡Entonces, las unidades de masa atómicas no son parte del sistema atómico de unidades! 1 amu es aproximadamente igual a 1800 masas de electrones (unidades de masa del sistema atómico de unidades). Este malentendido surgió históricamente: surgió en la comunidad química en el siglo XIX, y el sistema atómico de unidades en la primera mitad del siglo XX en la comunidad física. Para evitar esta confusión, IUPAC renombró el amu en los daltons, y desde los años 90 forzando activamente esta designación, pero, desafortunadamente, no tuvo mucho éxito.

Catálisis de muones en términos de química cuántica. Parte I: hidrógeno ordinario vs. muon hidrógeno