Comprender el Q-learning, el problema "Caminar sobre una roca"

Hola Habr! Les traigo a su atención una traducción del artículo "Entendiendo Q-Learning, el problema de Cliff Walking" de Lucas Vázquez .

En la última publicación, presentamos el problema "Caminar sobre una roca" y nos decidimos por un algoritmo terrible que no tenía sentido. Esta vez revelaremos los secretos de esta caja gris y veremos que no da tanto miedo.

Resumen

Llegamos a la conclusión de que al maximizar la cantidad de recompensas futuras, también encontramos el camino más rápido hacia la meta, por lo que nuestro objetivo ahora es encontrar una manera de hacerlo.

Introducción a Q-Learning

• Comencemos construyendo una tabla que mida qué tan bien se desempeñará una determinada acción en cualquier estado (podemos medirla con un valor escalar simple, por lo que cuanto mayor sea el valor, mejor será la acción)
• Esta tabla tendrá una fila para cada estado y una columna para cada acción. En nuestro mundo, la cuadrícula tiene 48 estados (4 por Y por 12 por X) y se permiten 4 acciones (arriba, abajo, izquierda, derecha), por lo que la tabla será 48 x 4.
• Los valores almacenados en esta tabla se denominan "valores Q".
• Estas son estimaciones de la cantidad de recompensas futuras. En otras palabras, estiman cuántas recompensas más podemos obtener antes del final del juego, estar en el estado S y realizar la acción A.
• Inicializamos la tabla con valores aleatorios (o alguna constante, por ejemplo, todos ceros).

La "tabla Q" óptima tiene valores que nos permiten tomar las mejores acciones en cada estado, dándonos la mejor manera de ganar al final. El problema está resuelto, saludos, Robot Lords :).

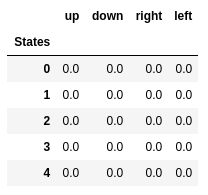Valores Q de los primeros cinco estados.

Q-learning

• Q-learning es un algoritmo que "aprende" estos valores.
• A cada paso obtenemos más información sobre el mundo.
• Esta información se utiliza para actualizar los valores en la tabla.

Por ejemplo, supongamos que estamos a un paso del objetivo (casilla [2, 11]), y si decidimos bajar, obtenemos una recompensa de 0 en lugar de -1.
Podemos usar esta información para actualizar el valor del par estado-acción en nuestra tabla, y la próxima vez que lo visitemos, ya sabremos que movernos hacia abajo nos da una recompensa de 0.

¡Ahora podemos difundir esta información aún más! Dado que ahora conocemos el camino hacia la meta desde el cuadrado [2, 11], cualquier acción que nos lleve al cuadrado [2, 11] también será buena, por lo tanto, actualizamos el valor Q del cuadrado, lo que nos lleva a [2, 11] estar más cerca de 0.

¡Y eso, damas y caballeros, es la esencia del Q-learning!

Tenga en cuenta que cada vez que alcanzamos la meta, aumentamos nuestro "mapa" de cómo lograr la meta en un cuadrado, por lo que después de un número suficiente de iteraciones tendremos un mapa completo que nos mostrará cómo llegar a la meta desde cada estado.

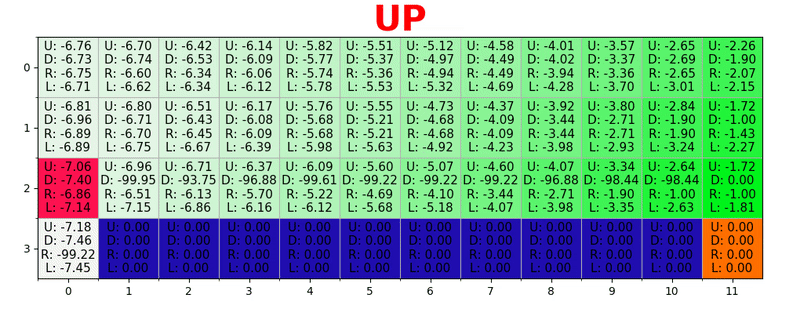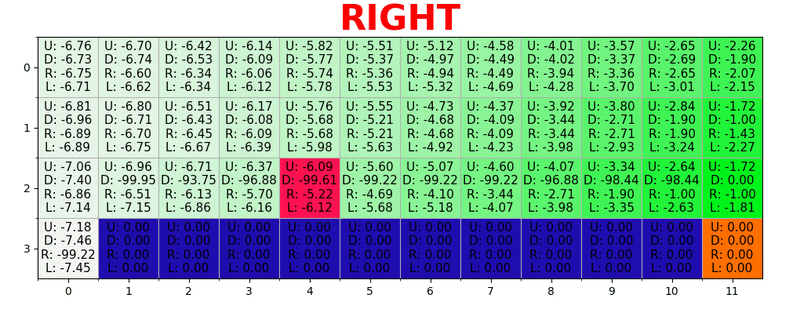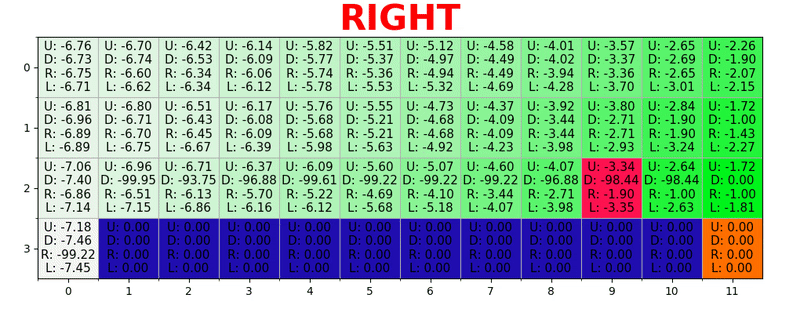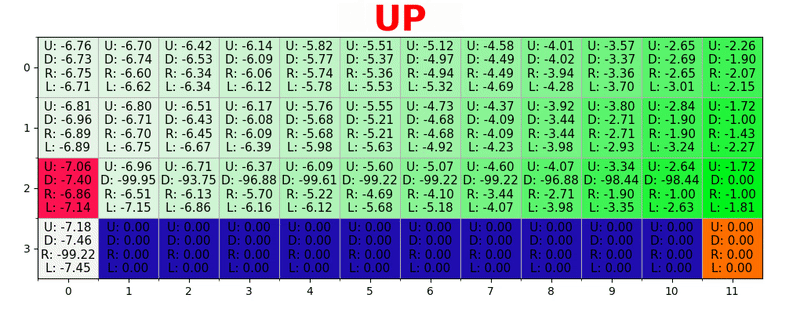Se genera una ruta al tomar la mejor acción en cada estado. La tecla verde representa el significado de una mejor acción, las teclas más saturadas representan un valor más alto. El texto representa un valor para cada acción (arriba, abajo, derecha, izquierda).

Ecuación de Bellman

Antes de hablar de código, hablemos de matemáticas: el concepto básico de Q-learning, la ecuación de Bellman.

• Primero olvidemos γ en esta ecuación
• La ecuación establece que el valor Q para un par de estado-acción en particular debería ser la recompensa recibida en la transición a un nuevo estado (al realizar esta acción), sumado al valor de la mejor acción en el siguiente estado.

En otras palabras, ¡difundimos información sobre los valores de las acciones paso a paso!

Pero podemos decidir que recibir una recompensa en este momento es más valioso que recibir una recompensa en el futuro, y por lo tanto tenemos γ, un número de 0 a 1 (generalmente de 0.9 a 0.99) que se multiplica por una recompensa en el futuro, descontando futuras recompensas.

Entonces, dado γ = 0.9 y aplicando esto a algunos estados de nuestro mundo (grilla), tenemos:

Podemos comparar estos valores con los anteriores en GIF y ver que son iguales.

Implementación

Ahora que tenemos una comprensión intuitiva de cómo funciona el Q-learning, podemos comenzar a pensar en implementar todo esto, y utilizaremos el pseudocódigo de Q-learning del libro de Sutton como guía.

Seudocódigo del libro de Sutton.

Código:

# Initialize Q arbitrarily, in this case a table full of zeros q_values = np.zeros((num_states, num_actions)) # Iterate over 500 episodes for _ in range(500): state = env.reset() done = False # While episode is not over while not done: # Choose action action = egreedy_policy(q_values, state, epsilon=0.1) # Do the action next_state, reward, done = env.step(action) # Update q_values td_target = reward + gamma * np.max(q_values[next_state]) td_error = td_target - q_values[state][action] q_values[state][action] += learning_rate * td_error # Update state state = next_state 

• Primero, decimos: "Para todos los estados y acciones, inicializamos Q (s, a) arbitrariamente", esto significa que podemos crear nuestra tabla de valores Q con cualquier valor que nos guste, pueden ser aleatorios, pueden ser cualquier tipo de permanente no importa. Vemos que en la línea 2 creamos una tabla llena de ceros.

También decimos: "El valor de Q para los estados finales es cero", no podemos realizar ninguna acción en los estados finales, por lo tanto, consideramos que el valor de todas las acciones en este estado es cero.

• Para cada episodio, tenemos que "inicializar S", esta es solo una forma elegante de decir "reiniciar el juego", en nuestro caso significa poner al jugador en la posición inicial; En nuestro mundo hay un método que hace exactamente eso, y lo llamamos en la línea 6.
• Para cada paso de tiempo (cada vez que necesitamos actuar), debemos elegir la acción obtenida de Q.

Recuerde, dije, “¿estamos tomando las acciones que son más valiosas en todas las condiciones?

Cuando hacemos esto, usamos nuestros valores Q para crear la política; en este caso será una política codiciosa, porque siempre tomamos acciones que, en nuestra opinión, son las mejores en todos los estados, por lo tanto, se dice que actuamos con avidez.

Basura

Pero hay un problema con este enfoque: imagina que estamos en un laberinto que tiene dos recompensas, una de las cuales es +1 y la otra es +100 (y cada vez que encontramos una de ellas, el juego termina). Dado que siempre tomamos medidas que consideramos las mejores, nos quedaremos atrapados con el primer premio encontrado, siempre volviendo a él, por lo tanto, si primero reconocemos el premio +1, entonces perderemos el gran premio +100.

Solución

Necesitamos asegurarnos de que hemos estudiado nuestro mundo lo suficiente (esta es una tarea increíblemente difícil). Aquí es donde entra en juego ε. ε en el algoritmo codicioso significa que debemos actuar con entusiasmo, PERO hacer acciones aleatorias como un porcentaje de ε a lo largo del tiempo, por lo que con un número infinito de intentos, debemos examinar todos los estados.

La acción se selecciona de acuerdo con esta estrategia en la línea 12, con epsilon = 0.1, lo que significa que estamos investigando el mundo el 10% del tiempo. La implementación de la política es la siguiente:

 def egreedy_policy(q_values, state, epsilon=0.1): # Get a random number from a uniform distribution between 0 and 1, # if the number is lower than epsilon choose a random action if np.random.random() < epsilon: return np.random.choice(4) # Else choose the action with the highest value else: return np.argmax(q_values[state]) 

En la línea 14 de la primera lista, llamamos al método de pasos para realizar la acción, el mundo nos devuelve el siguiente estado, recompensa e información sobre el final del juego.

De vuelta a las matemáticas:

Tenemos una ecuación larga, pensemos en ello:

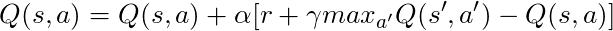
Si tomamos α = 1:

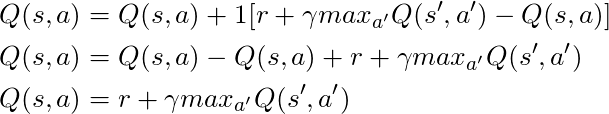
¡Que coincide exactamente con la ecuación de Bellman, que vimos hace unos párrafos! Entonces ya sabemos que esta es la línea responsable de diseminar información sobre los valores estatales.

Pero, por lo general, α (principalmente conocido como velocidad de aprendizaje) es mucho menor que 1, su objetivo principal es evitar grandes cambios en una actualización, por lo que en lugar de volar hacia la meta, nos acercamos lentamente. En nuestro enfoque tabular, establecer α = 1 no causa ningún problema, pero cuando se trabaja con redes neuronales (más sobre esto en los siguientes artículos), todo puede salirse de control fácilmente.

Mirando el código, vemos que en la línea 16 en la primera lista definimos td_target, este es el valor al que debemos acercarnos, pero en lugar de ir directamente a este valor en la línea 17, calculamos td_error, usaremos este valor en combinación con la velocidad aprendiendo a avanzar lentamente hacia la meta.

Recuerde que esta ecuación es una entidad de Q-Learning.

Ahora solo necesitamos actualizar nuestro estado, y todo está listo, esta es la línea 20. Repetimos este proceso hasta llegar al final del episodio, morir en las rocas o alcanzar la meta.

Conclusión

Ahora intuitivamente entendemos y sabemos cómo codificar Q-Learning (al menos la versión tabular), asegúrese de verificar todo el código utilizado para esta publicación, disponible en GitHub .

Visualización de la prueba del proceso de aprendizaje:

Tenga en cuenta que todas las acciones comienzan con un valor que excede su valor final, este es un truco para estimular la exploración del mundo.