Ya hemos discutido el
motor de indexación PostgreSQL y la
interfaz de los métodos de acceso , así como el
índice hash , uno de los métodos de acceso. Ahora consideraremos B-tree, el índice más tradicional y ampliamente utilizado. Este artículo es grande, así que sea paciente.
Btree
Estructura
El tipo de índice del árbol B, implementado como método de acceso "btree", es adecuado para los datos que se pueden ordenar. En otras palabras, los operadores "mayor", "mayor o igual", "menor", "menor o igual" e "igual" deben definirse para el tipo de datos. Tenga en cuenta que los mismos datos a veces se pueden ordenar de manera diferente, lo que
nos lleva de vuelta al concepto de familia de operadores.
Como siempre, las filas de índice del árbol B se empaquetan en páginas. En las páginas de hoja, estas filas contienen datos para indexar (claves) y referencias a filas de tabla (TID). En las páginas internas, cada fila hace referencia a una página secundaria del índice y contiene el valor mínimo en esta página.
Los árboles B tienen algunos rasgos importantes:
- Los árboles B están equilibrados, es decir, cada página de hoja está separada de la raíz por el mismo número de páginas internas. Por lo tanto, la búsqueda de cualquier valor lleva el mismo tiempo.
- Los árboles B son multibramificados, es decir, cada página (generalmente 8 KB) contiene muchos (cientos) TID. Como resultado, la profundidad de los árboles B es bastante pequeña, en realidad hasta 4-5 para tablas muy grandes.
- Los datos en el índice se ordenan en orden no decreciente (tanto entre páginas como dentro de cada página), y las páginas del mismo nivel están conectadas entre sí por una lista bidireccional. Por lo tanto, podemos obtener un conjunto de datos ordenado simplemente por una lista caminando en una u otra dirección sin volver a la raíz cada vez.
A continuación se muestra un ejemplo simplificado del índice en un campo con teclas enteras.
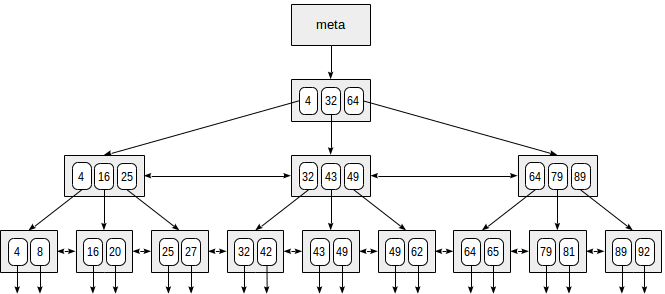
La primera página del índice es una metapágina, que hace referencia a la raíz del índice. Los nodos internos se encuentran debajo de la raíz, y las páginas de hoja están en la fila inferior. Las flechas hacia abajo representan referencias de nodos de hoja a filas de tabla (TID).
Búsqueda por igualdad
Consideremos la búsqueda de un valor en un árbol por la condición "
indexed-field =
expression ". Digamos que estamos interesados en la clave del 49.

La búsqueda comienza con el nodo raíz, y necesitamos determinar a cuál de los nodos hijos descender. Conociendo las claves en el nodo raíz (4, 32, 64), por lo tanto, calculamos los rangos de valores en los nodos secundarios. Como 32 ≤ 49 <64, debemos descender al segundo nodo hijo. A continuación, el mismo proceso se repite recursivamente hasta llegar a un nodo hoja desde el que se pueden obtener los TID necesarios.
En realidad, una serie de detalles complican este proceso aparentemente simple. Por ejemplo, un índice puede contener claves no únicas y puede haber tantos valores iguales que no caben en una página. Volviendo a nuestro ejemplo, parece que deberíamos descender del nodo interno sobre la referencia al valor de 49. Pero, como se desprende de la figura, de esta manera omitiremos una de las teclas "49" en la página de hoja anterior. . Por lo tanto, una vez que hayamos encontrado una clave exactamente igual en una página interna, tenemos que descender una posición hacia la izquierda y luego mirar a través de las filas de índice del nivel subyacente de izquierda a derecha en busca de la clave buscada.
(Otra complicación es que durante la búsqueda, otros procesos pueden cambiar los datos: el árbol se puede reconstruir, las páginas se pueden dividir en dos, etc. Todos los algoritmos están diseñados para que estas operaciones concurrentes no interfieran entre sí y no causen bloqueos adicionales siempre que sea posible, pero evitaremos expandirnos en esto).
Búsqueda por desigualdad
Al buscar por la condición "
expresión de campo indexado ≤" (o "
expresión de campo indexado ≥"), primero encontramos un valor (si lo hay) en el índice por la condición de igualdad "
campo indexado =
expresión " y luego recorremos hojas de hoja en la dirección adecuada hasta el final.
La figura ilustra este proceso para n ≤ 35:

Los operadores "mayor" y "menor" son compatibles de manera similar, excepto que el valor encontrado inicialmente debe descartarse.
Buscar por rango
Al buscar por rango "
expresión1 ≤
campo indexado ≤
expresión2 ", encontramos un valor por condición "
campo indexado =
expresión1 ", y luego seguimos caminando a través de las páginas mientras se cumple la condición "
campo indexado ≤
expresión2 "; o viceversa: comience con la segunda expresión y camine en dirección opuesta hasta llegar a la primera expresión.
La figura muestra este proceso para la condición 23 ≤ n ≤ 64:

Ejemplo
Veamos un ejemplo de cómo se ven los planes de consulta. Como de costumbre, usamos la base de datos de demostración, y esta vez consideraremos la tabla de aviones. Contiene tan solo nueve filas, y el planificador elegiría no usar el índice ya que la tabla completa se ajusta a una página. Pero esta tabla es interesante para nosotros con un propósito ilustrativo.
demo=# select * from aircrafts;
aircraft_code | model | range ---------------+---------------------+------- 773 | Boeing 777-300 | 11100 763 | Boeing 767-300 | 7900 SU9 | Sukhoi SuperJet-100 | 3000 320 | Airbus A320-200 | 5700 321 | Airbus A321-200 | 5600 319 | Airbus A319-100 | 6700 733 | Boeing 737-300 | 4200 CN1 | Cessna 208 Caravan | 1200 CR2 | Bombardier CRJ-200 | 2700 (9 rows)
demo=# create index on aircrafts(range); demo=# set enable_seqscan = off;
(O explícitamente, "crear índice en aeronaves usando btree (rango)", pero es un árbol B que se construye por defecto).
Búsqueda por igualdad:
demo=# explain(costs off) select * from aircrafts where range = 3000;
QUERY PLAN --------------------------------------------------- Index Scan using aircrafts_range_idx on aircrafts Index Cond: (range = 3000) (2 rows)
Búsqueda por desigualdad:
demo=# explain(costs off) select * from aircrafts where range < 3000;
QUERY PLAN --------------------------------------------------- Index Scan using aircrafts_range_idx on aircrafts Index Cond: (range < 3000) (2 rows)
Y por rango:
demo=# explain(costs off) select * from aircrafts where range between 3000 and 5000;
QUERY PLAN ----------------------------------------------------- Index Scan using aircrafts_range_idx on aircrafts Index Cond: ((range >= 3000) AND (range <= 5000)) (2 rows)
Clasificación
Una vez más, enfaticemos el punto de que con cualquier tipo de exploración (índice, solo índice o mapa de bits), el método de acceso "btree" devuelve datos ordenados, que podemos ver claramente en las figuras anteriores.
Por lo tanto, si una tabla tiene un índice en la condición de clasificación, el optimizador considerará ambas opciones: exploración de índice de la tabla, que devuelve fácilmente los datos ordenados, y exploración secuencial de la tabla con la clasificación posterior del resultado.
Orden de clasificación
Al crear un índice, podemos especificar explícitamente el orden de clasificación. Por ejemplo, podemos crear un índice por rangos de vuelo de esta manera en particular:
demo=# create index on aircrafts(range desc);
En este caso, los valores más grandes aparecerían en el árbol a la izquierda, mientras que los valores más pequeños aparecerían a la derecha. ¿Por qué puede ser necesario si podemos recorrer los valores indexados en cualquier dirección?
El propósito es índices de múltiples columnas. Creemos una vista para mostrar modelos de aeronaves con una división convencional en naves de corto, mediano y largo alcance:
demo=# create view aircrafts_v as select model, case when range < 4000 then 1 when range < 10000 then 2 else 3 end as class from aircrafts; demo=# select * from aircrafts_v;
model | class ---------------------+------- Boeing 777-300 | 3 Boeing 767-300 | 2 Sukhoi SuperJet-100 | 1 Airbus A320-200 | 2 Airbus A321-200 | 2 Airbus A319-100 | 2 Boeing 737-300 | 2 Cessna 208 Caravan | 1 Bombardier CRJ-200 | 1 (9 rows)
Y creemos un índice (usando la expresión):
demo=# create index on aircrafts( (case when range < 4000 then 1 when range < 10000 then 2 else 3 end), model);
Ahora podemos usar este índice para obtener datos ordenados por ambas columnas en orden ascendente:
demo=# select class, model from aircrafts_v order by class, model;
class | model -------+--------------------- 1 | Bombardier CRJ-200 1 | Cessna 208 Caravan 1 | Sukhoi SuperJet-100 2 | Airbus A319-100 2 | Airbus A320-200 2 | Airbus A321-200 2 | Boeing 737-300 2 | Boeing 767-300 3 | Boeing 777-300 (9 rows)
demo=# explain(costs off) select class, model from aircrafts_v order by class, model;
QUERY PLAN -------------------------------------------------------- Index Scan using aircrafts_case_model_idx on aircrafts (1 row)
Del mismo modo, podemos realizar la consulta para ordenar los datos en orden descendente:
demo=# select class, model from aircrafts_v order by class desc, model desc;
class | model -------+--------------------- 3 | Boeing 777-300 2 | Boeing 767-300 2 | Boeing 737-300 2 | Airbus A321-200 2 | Airbus A320-200 2 | Airbus A319-100 1 | Sukhoi SuperJet-100 1 | Cessna 208 Caravan 1 | Bombardier CRJ-200 (9 rows)
demo=# explain(costs off) select class, model from aircrafts_v order by class desc, model desc;
QUERY PLAN ----------------------------------------------------------------- Index Scan BACKWARD using aircrafts_case_model_idx on aircrafts (1 row)
Sin embargo, no podemos usar este índice para ordenar los datos por una columna en orden descendente y por la otra columna en orden ascendente. Esto requerirá ordenar por separado:
demo=# explain(costs off) select class, model from aircrafts_v order by class ASC, model DESC;
QUERY PLAN ------------------------------------------------- Sort Sort Key: (CASE ... END), aircrafts.model DESC -> Seq Scan on aircrafts (3 rows)
(Tenga en cuenta que, como último recurso, el planificador eligió el escaneo secuencial independientemente de la configuración "enable_seqscan = off" realizada anteriormente. Esto se debe a que en realidad esta configuración no prohíbe el escaneo de la tabla, sino que solo establece su costo astronómico; mire el plan con "Costos en").
Para hacer que esta consulta use el índice, este último debe construirse con la dirección de clasificación necesaria:
demo=# create index aircrafts_case_asc_model_desc_idx on aircrafts( (case when range < 4000 then 1 when range < 10000 then 2 else 3 end) ASC, model DESC); demo=# explain(costs off) select class, model from aircrafts_v order by class ASC, model DESC;
QUERY PLAN ----------------------------------------------------------------- Index Scan using aircrafts_case_asc_model_desc_idx on aircrafts (1 row)
Orden de columnas
Otro problema que surge cuando se usan índices de columnas múltiples es el orden de enumerar columnas en un índice. Para B-tree, este orden es de gran importancia: los datos dentro de las páginas se ordenarán por el primer campo, luego por el segundo, y así sucesivamente.
Podemos representar el índice que construimos en intervalos de rango y modelos de manera simbólica de la siguiente manera:

En realidad, un índice tan pequeño seguramente se ajustará a una página raíz. En la figura, se distribuye deliberadamente entre varias páginas para mayor claridad.
Está claro en este gráfico que la búsqueda por predicados como "class = 3" (buscar solo por el primer campo) o "class = 3 and model = 'Boeing 777-300'" (buscar por ambos campos) funcionará eficientemente.
Sin embargo, la búsqueda por el predicado "modelo = 'Boeing 777-300'" será mucho menos eficiente: comenzando con la raíz, no podemos determinar a qué nodo hijo descender, por lo tanto, tendremos que descender a todos ellos. Esto no significa que un índice como este no se pueda usar nunca; su eficiencia está en juego. Por ejemplo, si tuviéramos tres clases de aviones y una gran cantidad de modelos en cada clase, tendríamos que revisar aproximadamente un tercio del índice y esto podría haber sido más eficiente que el escaneo completo de la tabla ... o no.
Sin embargo, si creamos un índice como este:
demo=# create index on aircrafts( model, (case when range < 4000 then 1 when range < 10000 then 2 else 3 end));
el orden de los campos cambiará:

Con este índice, la búsqueda por el predicado "model = 'Boeing 777-300'" funcionará de manera eficiente, pero la búsqueda por el predicado "class = 3" no lo hará.
Nulos
El método de acceso "Btree" indexa NULL y admite la búsqueda por condiciones IS NULL y IS NOT NULL.
Consideremos la tabla de vuelos, donde ocurren NULL:
demo=# create index on flights(actual_arrival); demo=# explain(costs off) select * from flights where actual_arrival is null;
QUERY PLAN ------------------------------------------------------- Bitmap Heap Scan on flights Recheck Cond: (actual_arrival IS NULL) -> Bitmap Index Scan on flights_actual_arrival_idx Index Cond: (actual_arrival IS NULL) (4 rows)
Los NULL se encuentran en uno u otro extremo de los nodos hoja, dependiendo de cómo se creó el índice (NULLS FIRST o NULLS LAST). Esto es importante si una consulta incluye la clasificación: el índice se puede usar si el comando SELECT especifica el mismo orden de NULL en su cláusula ORDER BY que el orden especificado para el índice creado (NULLS FIRST o NULLS LAST).
En el siguiente ejemplo, estas órdenes son las mismas, por lo tanto, podemos usar el índice:
demo=# explain(costs off) select * from flights order by actual_arrival NULLS LAST;
QUERY PLAN -------------------------------------------------------- Index Scan using flights_actual_arrival_idx on flights (1 row)
Y aquí estas órdenes son diferentes, y el optimizador elige el escaneo secuencial con la clasificación posterior:
demo=# explain(costs off) select * from flights order by actual_arrival NULLS FIRST;
QUERY PLAN ---------------------------------------- Sort Sort Key: actual_arrival NULLS FIRST -> Seq Scan on flights (3 rows)
Para usar el índice, debe crearse con NULL ubicados al principio:
demo=# create index flights_nulls_first_idx on flights(actual_arrival NULLS FIRST); demo=# explain(costs off) select * from flights order by actual_arrival NULLS FIRST;
QUERY PLAN ----------------------------------------------------- Index Scan using flights_nulls_first_idx on flights (1 row)
Cuestiones como esta ciertamente son causadas por que los NULL no se pueden ordenar, es decir, el resultado de la comparación de NULL y cualquier otro valor no está definido:
demo=# \pset null NULL demo=# select null < 42;
?column? ---------- NULL (1 row)
Esto va en contra del concepto de árbol B y no encaja en el patrón general. Los NULL, sin embargo, juegan un papel tan importante en las bases de datos que siempre tenemos que hacer excepciones para ellos.
Dado que los NULL se pueden indexar, es posible usar un índice incluso sin ninguna condición impuesta en la tabla (ya que el índice contiene información sobre todas las filas de la tabla con seguridad). Esto puede tener sentido si la consulta requiere ordenar datos y el índice asegura el orden necesario. En este caso, el planificador puede elegir el acceso al índice para guardar en una clasificación separada.
Propiedades
Veamos las propiedades del método de acceso "btree" (
ya se han proporcionado consultas ).
amname | name | pg_indexam_has_property --------+---------------+------------------------- btree | can_order | t btree | can_unique | t btree | can_multi_col | t btree | can_exclude | t
Como hemos visto, B-tree puede ordenar datos y admite singularidad, y este es el único método de acceso que nos proporciona propiedades como estas. Los índices de varias columnas también están permitidos, pero otros métodos de acceso (aunque no todos) también pueden admitir dichos índices. Discutiremos el soporte de la restricción EXCLUDE la próxima vez, y no sin razón.
name | pg_index_has_property ---------------+----------------------- clusterable | t index_scan | t bitmap_scan | t backward_scan | t
El método de acceso "Btree" admite ambas técnicas para obtener valores: exploración de índice, así como exploración de mapa de bits. Y como pudimos ver, el método de acceso puede caminar a través del árbol tanto "hacia adelante" como "hacia atrás".
name | pg_index_column_has_property --------------------+------------------------------ asc | t desc | f nulls_first | f nulls_last | t orderable | t distance_orderable | f returnable | t search_array | t search_nulls | t
Las primeras cuatro propiedades de esta capa explican cómo se ordenan exactamente los valores de una determinada columna específica. En este ejemplo, los valores se ordenan en orden ascendente ("asc") y los NULL se proporcionan al final ("nulls_last"). Pero como ya hemos visto, otras combinaciones son posibles.
La propiedad "Search_array" indica que el índice admite expresiones como esta:
demo=# explain(costs off) select * from aircrafts where aircraft_code in ('733','763','773');
QUERY PLAN ----------------------------------------------------------------- Index Scan using aircrafts_pkey on aircrafts Index Cond: (aircraft_code = ANY ('{733,763,773}'::bpchar[])) (2 rows)
La propiedad "Retornable" indica la compatibilidad con la exploración de solo índice, lo cual es razonable ya que las filas del índice almacenan valores indexados (a diferencia del índice hash, por ejemplo). Aquí tiene sentido decir algunas palabras sobre los índices de cobertura basados en B-tree.
Índices únicos con filas adicionales
Como discutimos
anteriormente , un índice de cobertura es el que almacena todos los valores necesarios para una consulta, no se requiere acceso a la tabla en sí (casi). Un índice único puede cubrir específicamente.
Pero supongamos que queremos agregar columnas adicionales necesarias para una consulta al índice único. Sin embargo, la unicidad de tales valores compuestos no garantiza la unicidad de la clave, y luego se necesitarán dos índices en las mismas columnas: uno único para soportar la restricción de integridad y otro para ser utilizado como cobertura. Esto es ineficiente con seguridad.
En nuestra empresa, Anastasiya Lubennikova
lubennikovaav mejoró el método "btree" para que se pudieran incluir columnas adicionales, no únicas, en un índice único. Esperamos que este parche sea adoptado por la comunidad para formar parte de PostgreSQL, pero esto no sucederá tan pronto como en la versión 10. En este punto, el parche está disponible en Pro Standard 9.5+, y esto es lo que parece me gusta
De hecho, este parche se comprometió con PostgreSQL 11.
Consideremos la tabla de reservas:
demo=# \d bookings
Table "bookings.bookings" Column | Type | Modifiers --------------+--------------------------+----------- book_ref | character(6) | not null book_date | timestamp with time zone | not null total_amount | numeric(10,2) | not null Indexes: "bookings_pkey" PRIMARY KEY, btree (book_ref) Referenced by: TABLE "tickets" CONSTRAINT "tickets_book_ref_fkey" FOREIGN KEY (book_ref) REFERENCES bookings(book_ref)
En esta tabla, la clave primaria (book_ref, código de reserva) es proporcionada por un índice "btree" regular. Creemos un nuevo índice único con una columna adicional:
demo=# create unique index bookings_pkey2 on bookings(book_ref) INCLUDE (book_date);
Ahora reemplazamos el índice existente por uno nuevo (en la transacción, para aplicar todos los cambios simultáneamente):
demo=# begin; demo=# alter table bookings drop constraint bookings_pkey cascade; demo=# alter table bookings add primary key using index bookings_pkey2; demo=# alter table tickets add foreign key (book_ref) references bookings (book_ref); demo=# commit;
Esto es lo que obtenemos:
demo=# \d bookings
Table "bookings.bookings" Column | Type | Modifiers --------------+--------------------------+----------- book_ref | character(6) | not null book_date | timestamp with time zone | not null total_amount | numeric(10,2) | not null Indexes: "bookings_pkey2" PRIMARY KEY, btree (book_ref) INCLUDE (book_date) Referenced by: TABLE "tickets" CONSTRAINT "tickets_book_ref_fkey" FOREIGN KEY (book_ref) REFERENCES bookings(book_ref)
Ahora, el mismo índice funciona como único y sirve como índice de cobertura para esta consulta, por ejemplo:
demo=# explain(costs off) select book_ref, book_date from bookings where book_ref = '059FC4';
QUERY PLAN -------------------------------------------------- Index Only Scan using bookings_pkey2 on bookings Index Cond: (book_ref = '059FC4'::bpchar) (2 rows)
Creación del índice.
Es bien sabido, pero no menos importante, que para una tabla de gran tamaño, es mejor cargar datos allí sin índices y crear los índices necesarios más adelante. Esto no solo es más rápido, sino que lo más probable es que el índice tenga un tamaño más pequeño.
La cuestión es que la creación del índice "btree" utiliza un proceso más eficiente que la inserción de valores en fila en el árbol. Aproximadamente, se ordenan todos los datos disponibles en la tabla y se crean páginas de hoja de estos datos. Luego, las páginas internas se "construyen" sobre esta base hasta que toda la pirámide converja a la raíz.
La velocidad de este proceso depende del tamaño de RAM disponible, que está limitado por el parámetro "maintenance_work_mem". Por lo tanto, aumentar el valor del parámetro puede acelerar el proceso. Para índices únicos, se asigna memoria de tamaño "work_mem" además de "maintenance_work_mem".
Semántica de comparación
La última vez que mencionamos que PostgreSQL necesita saber qué funciones hash solicitar valores de diferentes tipos y que esta asociación se almacena en el método de acceso "hash". Del mismo modo, el sistema debe descubrir cómo ordenar los valores. Esto es necesario para clasificaciones, agrupaciones (a veces), combinaciones de fusión, etc. PostgreSQL no se une a los nombres de los operadores (como>, <, =) ya que los usuarios pueden definir su propio tipo de datos y dar a los operadores correspondientes diferentes nombres. Una familia de operadores utilizada por el método de acceso "btree" define los nombres de los operadores en su lugar.
Por ejemplo, estos operadores de comparación se usan en la familia de operadores "bool_ops":
postgres=# select amop.amopopr::regoperator as opfamily_operator, amop.amopstrategy from pg_am am, pg_opfamily opf, pg_amop amop where opf.opfmethod = am.oid and amop.amopfamily = opf.oid and am.amname = 'btree' and opf.opfname = 'bool_ops' order by amopstrategy;
opfamily_operator | amopstrategy ---------------------+-------------- <(boolean,boolean) | 1 <=(boolean,boolean) | 2 =(boolean,boolean) | 3 >=(boolean,boolean) | 4 >(boolean,boolean) | 5 (5 rows)
Aquí podemos ver cinco operadores de comparación, pero como ya se mencionó, no debemos confiar en sus nombres. Para determinar qué comparación hace cada operador, se introduce el concepto de estrategia. Se definen cinco estrategias para describir la semántica del operador:
- 1 - menos
- 2 - menos o igual
- 3 - igual
- 4 - mayor o igual
- 5 - mayor
Algunas familias de operadores pueden contener varios operadores que implementan una estrategia. Por ejemplo, la familia de operadores "integer_ops" contiene los siguientes operadores para la estrategia 1:
postgres=# select amop.amopopr::regoperator as opfamily_operator from pg_am am, pg_opfamily opf, pg_amop amop where opf.opfmethod = am.oid and amop.amopfamily = opf.oid and am.amname = 'btree' and opf.opfname = 'integer_ops' and amop.amopstrategy = 1 order by opfamily_operator;
opfamily_operator ---------------------- <(integer,bigint) <(smallint,smallint) <(integer,integer) <(bigint,bigint) <(bigint,integer) <(smallint,integer) <(integer,smallint) <(smallint,bigint) <(bigint,smallint) (9 rows)
Gracias a esto, el optimizador puede evitar la conversión de tipos al comparar valores de diferentes tipos contenidos en una familia de operadores.
Compatibilidad con índices para un nuevo tipo de datos
La documentación proporciona
un ejemplo de creación de un nuevo tipo de datos para números complejos y de una clase de operador para ordenar valores de este tipo. Este ejemplo usa lenguaje C, que es absolutamente razonable cuando la velocidad es crítica. Pero nada nos impide usar SQL puro para el mismo experimento para tratar de comprender mejor la semántica de comparación.
Creemos un nuevo tipo compuesto con dos campos: partes reales e imaginarias.
postgres=# create type complex as (re float, im float);
Podemos crear una tabla con un campo del nuevo tipo y agregar algunos valores a la tabla:
postgres=# create table numbers(x complex); postgres=# insert into numbers values ((0.0, 10.0)), ((1.0, 3.0)), ((1.0, 1.0));
Ahora surge una pregunta: ¿cómo ordenar números complejos si no se define una relación de orden para ellos en el sentido matemático?
Como resultado, los operadores de comparación ya están definidos para nosotros:
postgres=# select * from numbers order by x;
x -------- (0,10) (1,1) (1,3) (3 rows)
De manera predeterminada, la ordenación es por componentes para un tipo compuesto: primero se comparan los campos, luego los segundos campos, y así sucesivamente, aproximadamente de la misma manera que las cadenas de texto se comparan carácter por carácter. Pero podemos definir un orden diferente. Por ejemplo, los números complejos pueden tratarse como vectores y ordenarse por el módulo (longitud), que se calcula como la raíz cuadrada de la suma de los cuadrados de las coordenadas (el teorema de Pitágoras). Para definir dicho orden, creemos una función auxiliar que calcule el módulo:
postgres=# create function modulus(a complex) returns float as $$ select sqrt(a.re*a.re + a.im*a.im); $$ immutable language sql;
Ahora definiremos sistemáticamente las funciones para los cinco operadores de comparación utilizando esta función auxiliar:
postgres=# create function complex_lt(a complex, b complex) returns boolean as $$ select modulus(a) < modulus(b); $$ immutable language sql; postgres=# create function complex_le(a complex, b complex) returns boolean as $$ select modulus(a) <= modulus(b); $$ immutable language sql; postgres=# create function complex_eq(a complex, b complex) returns boolean as $$ select modulus(a) = modulus(b); $$ immutable language sql; postgres=# create function complex_ge(a complex, b complex) returns boolean as $$ select modulus(a) >= modulus(b); $$ immutable language sql; postgres=# create function complex_gt(a complex, b complex) returns boolean as $$ select modulus(a) > modulus(b); $$ immutable language sql;
Y crearemos los operadores correspondientes. Para ilustrar que no necesitan llamarse ">", "<", etc., démosles nombres "extraños".
postgres=# create operator #<#(leftarg=complex, rightarg=complex, procedure=complex_lt); postgres=# create operator #<=#(leftarg=complex, rightarg=complex, procedure=complex_le); postgres=# create operator #=#(leftarg=complex, rightarg=complex, procedure=complex_eq); postgres=# create operator #>=#(leftarg=complex, rightarg=complex, procedure=complex_ge); postgres=# create operator #>#(leftarg=complex, rightarg=complex, procedure=complex_gt);
En este punto, podemos comparar números:
postgres=# select (1.0,1.0)::complex #<# (1.0,3.0)::complex;
?column? ---------- t (1 row)
Además de cinco operadores, el método de acceso "btree" requiere que se defina una función más (excesiva pero conveniente): debe devolver -1, 0 o 1 si el primer valor es menor, igual o mayor que el segundo uno. Esta función auxiliar se llama soporte. Otros métodos de acceso pueden requerir la definición de otras funciones de soporte.
postgres=# create function complex_cmp(a complex, b complex) returns integer as $$ select case when modulus(a) < modulus(b) then -1 when modulus(a) > modulus(b) then 1 else 0 end; $$ language sql;
Ahora estamos listos para crear una clase de operador (y la familia de operadores con el mismo nombre se creará automáticamente):
postgres=# create operator class complex_ops default for type complex using btree as operator 1 #<#, operator 2 #<=#, operator 3 #=#, operator 4 #>=#, operator 5 #>#, function 1 complex_cmp(complex,complex);
Ahora la clasificación funciona según lo deseado:
postgres=# select * from numbers order by x;
x -------- (1,1) (1,3) (0,10) (3 rows)
Y sin duda será compatible con el índice "btree".
Para completar la imagen, puede obtener funciones de soporte utilizando esta consulta:
postgres=# select amp.amprocnum, amp.amproc, amp.amproclefttype::regtype, amp.amprocrighttype::regtype from pg_opfamily opf, pg_am am, pg_amproc amp where opf.opfname = 'complex_ops' and opf.opfmethod = am.oid and am.amname = 'btree' and amp.amprocfamily = opf.oid;
amprocnum | amproc | amproclefttype | amprocrighttype -----------+-------------+----------------+----------------- 1 | complex_cmp | complex | complex (1 row)
Internos
Podemos explorar la estructura interna del árbol B usando la extensión "pageinspect".
demo=# create extension pageinspect;
Metapágina del índice:
demo=# select * from bt_metap('ticket_flights_pkey');
magic | version | root | level | fastroot | fastlevel --------+---------+------+-------+----------+----------- 340322 | 2 | 164 | 2 | 164 | 2 (1 row)
Lo más interesante aquí es el nivel de índice: el índice en dos columnas para una tabla con un millón de filas requiere tan solo 2 niveles (sin incluir la raíz).
Información estadística sobre el bloque 164 (raíz):
demo=# select type, live_items, dead_items, avg_item_size, page_size, free_size from bt_page_stats('ticket_flights_pkey',164);
type | live_items | dead_items | avg_item_size | page_size | free_size ------+------------+------------+---------------+-----------+----------- r | 33 | 0 | 31 | 8192 | 6984 (1 row)
Y los datos en el bloque (el campo "datos", que aquí se sacrifica al ancho de la pantalla, contiene el valor de la clave de indexación en representación binaria):
demo=# select itemoffset, ctid, itemlen, left(data,56) as data from bt_page_items('ticket_flights_pkey',164) limit 5;
itemoffset | ctid | itemlen | data ------------+---------+---------+---------------------------------------------------------- 1 | (3,1) | 8 | 2 | (163,1) | 32 | 1d 30 30 30 35 34 33 32 33 30 35 37 37 31 00 00 ff 5f 00 3 | (323,1) | 32 | 1d 30 30 30 35 34 33 32 34 32 33 36 36 32 00 00 4f 78 00 4 | (482,1) | 32 | 1d 30 30 30 35 34 33 32 35 33 30 38 39 33 00 00 4d 1e 00 5 | (641,1) | 32 | 1d 30 30 30 35 34 33 32 36 35 35 37 38 35 00 00 2b 09 00 (5 rows)
El primer elemento pertenece a las técnicas y especifica el límite superior de todos los elementos en el bloque (un detalle de implementación que no discutimos), mientras que los datos en sí comienzan con el segundo elemento. Está claro que el nodo secundario más a la izquierda es el bloque 163, seguido del bloque 323, y así sucesivamente. Ellos, a su vez, pueden explorarse utilizando las mismas funciones.
Ahora, siguiendo una buena tradición, tiene sentido leer la documentación,
README y el código fuente.
Sin embargo, una extensión potencialmente útil más es "
amcheck ", que se incorporará en PostgreSQL 10, y para versiones anteriores puede obtenerla de
github . Esta extensión verifica la consistencia lógica de los datos en los árboles B y nos permite detectar fallas por adelantado.
Eso es cierto, "amcheck" es una parte de PostgreSQL a partir de la versión 10.
Sigue leyendo .