Finalmente, apareció una guía en ruso para el idioma Julia . Proporciona una introducción completa al lenguaje para aquellos que tienen poca experiencia en programación (el resto será útil para el desarrollo general), también hay una introducción al aprendizaje automático y un montón de tareas para consolidar el material.
Durante la búsqueda, me encontré con un curso de programación para economistas (además de Julia, también hay Python). Los experimentados pueden ir a un curso rápido o leer el libro Cómo pensar como un informático
La siguiente es una traducción del material del blog de Christopher Rackauckas 7 Julia Gotchas y Cómo manejarlos
Permítanme comenzar diciendo que Julia es un lenguaje maravilloso. La amo, esto es lo que considero el lenguaje más poderoso e intuitivo que he usado. Este es sin duda mi idioma favorito. Sin embargo, hay algunas "trampas", pequeñas cosas difíciles que debes saber. Cada idioma los tiene, y una de las primeras cosas que debe hacer para dominar el idioma es descubrir cuáles son y cómo evitarlos. El objetivo de esta publicación es ayudarlo a acelerar este proceso al exponer algunos de los
Julia es un buen lenguaje para entender lo que está sucediendo, porque no tiene magia. Los desarrolladores de Julia querían tener reglas de conducta claramente definidas. Esto significa que todo comportamiento puede explicarse. Sin embargo, esto puede significar que tiene que esforzarse para comprender por qué esto y no lo otro está sucediendo. Es por eso que no solo voy a describir algunos problemas comunes, sino que también voy a explicar por qué surgen. Verás que hay algunos patrones muy similares, y una vez que te des cuenta de ellos, ya no te burlarás de ninguno de ellos. Debido a esto, Julia tiene una curva de aprendizaje un poco más pronunciada en comparación con lenguajes más simples como MATLAB / R / Python . Sin embargo, una vez que haya dominado esto, podrá utilizar completamente el laconismo de Julia para obtener el rendimiento de C / Fortran . Ahora cava más profundo.
Inesperadamente: REPL (terminal) tiene un alcance global
Este es, con mucho, el problema más común reportado por los nuevos usuarios de Julia. Alguien dirá: "Escuché, ¡Julia es rápida!", Abra REPL, escriba rápidamente un algoritmo conocido y ejecute este script. Después de su ejecución, miran el tiempo y dicen: "Espera un segundo, ¿por qué es lento, como en Python?" Dado que este es un problema tan importante y común, dediquemos un tiempo a explorar las razones por las que esto sucede para descubrir cómo evitarlo.
Una pequeña digresión: por qué Julia es rápida
Debe comprender que Julia no es solo una compilación de código, sino también una especialización de tipos (es decir, una compilación de código específica para estos tipos). Permítanme reiterar: Julia no es rápida, porque el código se compila utilizando el compilador JIT, más bien el secreto de la velocidad es que se compila el código específico del tipo.
Si necesita una historia completa, consulte algunas de las notas que escribí para el próximo seminario . La especificidad de tipo está determinada por el principio básico del diseño de Julia: despacho múltiple . Cuando escribes el código:
function f(a,b) return 2a+b end
Parece que esta es solo una f(2.0,3.0) , Julia ejecutará el código compilado, que toma dos números de coma flotante y devuelve 2a + b . Si llama a f(2,3) , Julia ejecutará otro código compilado que toma dos enteros y devuelve 2a + b . La función f es una abstracción o abreviatura para muchos métodos diferentes que tienen la misma forma, y dicho esquema de usar el símbolo f para llamar a todos estos métodos diferentes se denomina despacho múltiple. Y esto se aplica en todas partes: el operador + es en realidad una función que llamará a los métodos dependiendo de los tipos que vea. En realidad, Julia obtiene su velocidad porque el código compilado por ella conoce sus tipos y, por lo tanto, el código compilado que llama a f (2.0,3.0) es exactamente el código compilado que se obtiene al definir la misma función en C / Fortran . Puede verificar esto con la macro code_native para ver el ensamblado compilado:
@code_native f(2.0,3.0)
pushq %rbp movq %rsp, %rbp Source line: 2 vaddsd %xmm0, %xmm0, %xmm0 vaddsd %xmm1, %xmm0, %xmm0 popq %rbp retq nop
Este es el mismo ensamblado compilado que espera de una función en C / Fortran , y difiere del código de ensamblado para enteros:
@code_native f(2,3) pushq %rbp movq %rsp, %rbp Source line: 2 leaq (%rdx,%rcx,2), %rax popq %rbp retq nopw (%rax,%rax)
Esencia: REPL / Global Scope no permite especificidad de tipo
Esto nos lleva al punto principal: REPL / Global Scope es lento porque no permite la especificación de tipo. En primer lugar, tenga en cuenta que REPL es un ámbito global porque Julia permite un ámbito anidado para funciones. Por ejemplo, si definimos
function outer() a = 5 function inner() return 2a end b = inner() return 3a+b end
veremos que este código funciona. Esto se debe a que Julia le permite capturar
a=2.0; b=3.0 function linearcombo() return 2a+b end ans = linearcombo()
y
a = 2; b = 3 ans2= linearcombo()
Pregunta: ¿Qué tipos debe aceptar el compilador para b ? Tenga en cuenta que en este ejemplo, cambiamos los tipos y aún llamamos a la misma función. Puede tratar cualquier tipo que le agreguemos: flotante, enteros, matrices, tipos de usuarios extraños, etc. En Julia, esto significa que las variables deben estar encuadradas y los tipos se verifican cada vez que se usan. ¿Cómo crees que se ve el código compilado?
Voluminoso pushq %rbp movq %rsp, %rbp pushq %r15 pushq %r14 pushq %r12 pushq %rsi pushq %rdi pushq %rbx subq $96, %rsp movl $2147565792, %edi # imm = 0x800140E0 movabsq $jl_get_ptls_states, %rax callq *%rax movq %rax, %rsi leaq -72(%rbp), %r14 movq $0, -88(%rbp) vxorps %xmm0, %xmm0, %xmm0 vmovups %xmm0, -72(%rbp) movq $0, -56(%rbp) movq $10, -104(%rbp) movq (%rsi), %rax movq %rax, -96(%rbp) leaq -104(%rbp), %rax movq %rax, (%rsi) Source line: 3 movq pcre2_default_compile_context_8(%rdi), %rax movq %rax, -56(%rbp) movl $2154391480, %eax # imm = 0x806967B8 vmovq %rax, %xmm0 vpslldq $8, %xmm0, %xmm0 # xmm0 = zero,zero,zero,zero,zero,zero,zero,zero,xmm0[0,1,2,3,4,5,6,7] vmovdqu %xmm0, -80(%rbp) movq %rdi, -64(%rbp) movabsq $jl_apply_generic, %r15 movl $3, %edx movq %r14, %rcx callq *%r15 movq %rax, %rbx movq %rbx, -88(%rbp) movabsq $586874896, %r12 # imm = 0x22FB0010 movq (%r12), %rax testq %rax, %rax jne L198 leaq 98096(%rdi), %rcx movabsq $jl_get_binding_or_error, %rax movl $122868360, %edx # imm = 0x752D288 callq *%rax movq %rax, (%r12) L198: movq 8(%rax), %rax testq %rax, %rax je L263 movq %rax, -80(%rbp) addq $5498232, %rdi # imm = 0x53E578 movq %rdi, -72(%rbp) movq %rbx, -64(%rbp) movq %rax, -56(%rbp) movl $3, %edx movq %r14, %rcx callq *%r15 movq -96(%rbp), %rcx movq %rcx, (%rsi) addq $96, %rsp popq %rbx popq %rdi popq %rsi popq %r12 popq %r14 popq %r15 popq %rbp retq L263: movabsq $jl_undefined_var_error, %rax movl $122868360, %ecx # imm = 0x752D288 callq *%rax ud2 nopw (%rax,%rax)
Para lenguajes dinámicos sin especialización de tipo, este código inflado con todas las instrucciones adicionales es tan bueno como sea posible, por lo que Julia disminuye su velocidad. Para comprender por qué esto es tan importante, tenga en cuenta que cada fragmento de código que escribe en Julia se compila. Digamos que escribes un bucle en tu script:
a = 1 for i = 1:100 a += a + f(a) end
El compilador tendrá que compilar este bucle, pero como no puede garantizar que los tipos no cambien, conserva de forma conservadora un paño en todos los tipos, lo que conduce a una ejecución lenta.
Como evitar un problema
Hay varias formas de evitar este problema. La forma más fácil es envolver siempre sus scripts en funciones. Por ejemplo, el código anterior tomará la forma:
function geta(a) # can also just define a=1 here for i = 1:100 a += a + f(a) end return a end a = geta(1)
Esto le dará el mismo resultado, pero dado que el compilador puede especializarse en el tipo a , le proporcionará el código compilado que desee. Otra cosa que puede hacer es definir sus variables como constantes.
const b = 5
Al hacer esto, le dice al compilador que la variable no cambiará y, por lo tanto, podrá especializar todo el código que lo usa en el tipo que es actualmente. Hay una ligera peculiaridad de que Julia realmente le permite cambiar el valor de una constante, pero no un tipo. Por lo tanto, puede usar const para decirle al compilador que no cambiará el tipo. Sin embargo, tenga en cuenta que hay algunas pequeñas peculiaridades:
const a = 5 f() = a println(f()) # Prints 5 a = 6 println(f()) # Prints 5 # WARNING: redefining constant a
esto no funciona como se esperaba, porque el compilador, al darse cuenta de que conoce la respuesta a f () = a (ya que a es una constante), simplemente reemplazó la llamada a la función con la respuesta, dando un comportamiento diferente al de a si no fuera constante.
Moraleja: no escriba sus scripts directamente en REPL, siempre envuélvalos en una función.
Nezhdanchik dos: inestabilidad tipo
Entonces, acabo de expresar una opinión sobre la importancia de la especialización del código para los tipos de datos. Déjame hacerte una pregunta, ¿qué sucede cuando tus tipos pueden cambiar? Si adivinó: "Bueno, en este caso, no puede especializar el código compilado", tiene razón. Tal problema se conoce como inestabilidad de tipo. Pueden aparecer de manera diferente, pero un ejemplo común es que inicializa el valor con el simple, pero no necesariamente el tipo que debería ser. Por ejemplo, veamos:
function g() x=1 for i = 1:10 x = x/2 end return x end
Tenga en cuenta que 1/2 es un número de coma flotante en Julia. Por lo tanto, si comenzamos con x = 1 , el número entero cambiará a un número de coma flotante y, por lo tanto, la función debería compilar el bucle interno, como si pudiera ser de cualquier tipo. Si en cambio tuviéramos:
function h() x=1.0 for i = 1:10 x = x/2 end return x end
entonces toda la función podrá compilarse de manera óptima, sabiendo que x seguirá siendo un número de coma flotante (esta capacidad para que el compilador determine los tipos se llama inferencia de tipos). Podemos verificar el código compilado para ver la diferencia:
Tela nativa pushq %rbp movq %rsp, %rbp pushq %r15 pushq %r14 pushq %r13 pushq %r12 pushq %rsi pushq %rdi pushq %rbx subq $136, %rsp movl $2147565728, %ebx # imm = 0x800140A0 movabsq $jl_get_ptls_states, %rax callq *%rax movq %rax, -152(%rbp) vxorps %xmm0, %xmm0, %xmm0 vmovups %xmm0, -80(%rbp) movq $0, -64(%rbp) vxorps %ymm0, %ymm0, %ymm0 vmovups %ymm0, -128(%rbp) movq $0, -96(%rbp) movq $18, -144(%rbp) movq (%rax), %rcx movq %rcx, -136(%rbp) leaq -144(%rbp), %rcx movq %rcx, (%rax) movq $0, -88(%rbp) Source line: 4 movq %rbx, -104(%rbp) movl $10, %edi leaq 477872(%rbx), %r13 leaq 10039728(%rbx), %r15 leaq 8958904(%rbx), %r14 leaq 64(%rbx), %r12 leaq 10126032(%rbx), %rax movq %rax, -160(%rbp) nopw (%rax,%rax) L176: movq %rbx, -128(%rbp) movq -8(%rbx), %rax andq $-16, %rax movq %r15, %rcx cmpq %r13, %rax je L272 movq %rbx, -96(%rbp) movq -160(%rbp), %rcx cmpq $2147419568, %rax # imm = 0x7FFF05B0 je L272 movq %rbx, -72(%rbp) movq %r14, -80(%rbp) movq %r12, -64(%rbp) movl $3, %edx leaq -80(%rbp), %rcx movabsq $jl_apply_generic, %rax vzeroupper callq *%rax movq %rax, -88(%rbp) jmp L317 nopw %cs:(%rax,%rax) L272: movq %rcx, -120(%rbp) movq %rbx, -72(%rbp) movq %r14, -80(%rbp) movq %r12, -64(%rbp) movl $3, %r8d leaq -80(%rbp), %rdx movabsq $jl_invoke, %rax vzeroupper callq *%rax movq %rax, -112(%rbp) L317: movq (%rax), %rsi movl $1488, %edx # imm = 0x5D0 movl $16, %r8d movq -152(%rbp), %rcx movabsq $jl_gc_pool_alloc, %rax callq *%rax movq %rax, %rbx movq %r13, -8(%rbx) movq %rsi, (%rbx) movq %rbx, -104(%rbp) Source line: 3 addq $-1, %rdi jne L176 Source line: 6 movq -136(%rbp), %rax movq -152(%rbp), %rcx movq %rax, (%rcx) movq %rbx, %rax addq $136, %rsp popq %rbx popq %rdi popq %rsi popq %r12 popq %r13 popq %r14 popq %r15 popq %rbp retq nop
en contra
Hechizo de ensamblador ordenado pushq %rbp movq %rsp, %rbp movabsq $567811336, %rax # imm = 0x21D81D08 Source line: 6 vmovsd (%rax), %xmm0 # xmm0 = mem[0],zero popq %rbp retq nopw %cs:(%rax,%rax)
¡Qué diferencia en el número de cálculos para obtener el mismo valor!
Cómo encontrar y lidiar con la inestabilidad de tipos

En este punto, puede preguntar: "Bueno, ¿por qué no usar C para no tener que buscar estas inestabilidades?" La respuesta es:
- Fácil de encontrar
- Pueden ser de ayuda.
Puede manejar la inestabilidad con barreras funcionales.
Julia le da la macro code_warntype para mostrar dónde están las inestabilidades de tipo. Por ejemplo, si usamos esto en la función g que creamos:
@code_warntype g()
obtener el análisis Variables: #self#::#g x::ANY #temp#@_3::Int64 i::Int64 #temp#@_5::Core.MethodInstance #temp#@_6::Float64 Body: begin x::ANY = 1 # line 3: SSAValue(2) = (Base.select_value)((Base.sle_int)(1,10)::Bool,10,(Base.box)(Int64,(Base.sub_int)(1,1)))::Int64 #temp#@_3::Int64 = 1 5: unless (Base.box)(Base.Bool,(Base.not_int)((#temp#@_3::Int64 === (Base.box)(Int64,(Base.add_int)(SSAValue(2),1)))::Bool)) goto 30 SSAValue(3) = #temp#@_3::Int64 SSAValue(4) = (Base.box)(Int64,(Base.add_int)(#temp#@_3::Int64,1)) i::Int64 = SSAValue(3) #temp#@_3::Int64 = SSAValue(4) # line 4: unless (Core.isa)(x::UNION{FLOAT64,INT64},Float64)::ANY goto 15 #temp#@_5::Core.MethodInstance = MethodInstance for /(::Float64, ::Int64) goto 24 15: unless (Core.isa)(x::UNION{FLOAT64,INT64},Int64)::ANY goto 19 #temp#@_5::Core.MethodInstance = MethodInstance for /(::Int64, ::Int64) goto 24 19: goto 21 21: #temp#@_6::Float64 = (x::UNION{FLOAT64,INT64} / 2)::Float64 goto 26 24: #temp#@_6::Float64 = $(Expr(:invoke, :(#temp#@_5), :(Main./), :(x::Union{Float64,Int64}), 2)) 26: x::ANY = #temp#@_6::Float64 28: goto 5 30: # line 6: return x::UNION{FLOAT64,INT64} end::UNION{FLOAT64,INT64}
Tenga en cuenta que al principio decimos que el tipo x es Any . Utilizará cualquier tipo que no esté designado como strict type , es decir, es un tipo abstracto que necesita ser encuadrado / verificado en cada paso. Vemos que al final devolvemos x como UNION {FLOAT64, INT64} , que es otro tipo no estricto. Esto nos dice que el tipo code_warntype para h , obtenemos todos los tipos estrictos:
@code_warntype h() Variables: #self#::#h x::Float64 #temp#::Int64 i::Int64 Body: begin x::Float64 = 1.0 # line 3: SSAValue(2) = (Base.select_value)((Base.sle_int)(1,10)::Bool,10,(Base.box)(Int64,(Base.sub_int)(1,1)))::Int64 #temp#::Int64 = 1 5: unless (Base.box)(Base.Bool,(Base.not_int)((#temp#::Int64 === (Base.box)(Int64,(Base.add_int)(SSAValue(2),1)))::Bool)) goto 15 SSAValue(3) = #temp#::Int64 SSAValue(4) = (Base.box)(Int64,(Base.add_int)(#temp#::Int64,1)) i::Int64 = SSAValue(3) #temp#::Int64 = SSAValue(4) # line 4: x::Float64 = (Base.box)(Base.Float64,(Base.div_float)(x::Float64,(Base.box)(Float64,(Base.sitofp)(Float64,2)))) 13: goto 5 15: # line 6: return x::Float64 end::Float64
Esto indica que la función es de tipo estable y se compilará esencialmente en un código C óptimo. Por lo tanto, la inestabilidad de tipo no es difícil de encontrar. Lo que es más difícil es encontrar el diseño correcto. ¿Por qué resolver la inestabilidad de tipo? Este es un problema de larga data que ha llevado al hecho de que los idiomas escritos dinámicamente dominan el campo de juego de los scripts. La idea es que, en muchos casos, desee encontrar un compromiso entre rendimiento y confiabilidad.
Por ejemplo, puede leer una tabla desde una página web en la que los enteros se mezclan con números de coma flotante. En Julia, puede escribir su función de modo que si todos fueran números enteros, se compile bien, y si todos fueran números de coma flotante, también se compilaría bien. ¿Y si se mezclan? Esto seguirá funcionando. Esta es la flexibilidad / conveniencia que conocemos y amamos de un lenguaje como Python / R. Pero Julia le dirá directamente (a través de code_warntype ) cuando sacrifique el rendimiento.
Cómo lidiar con las inestabilidades de tipo
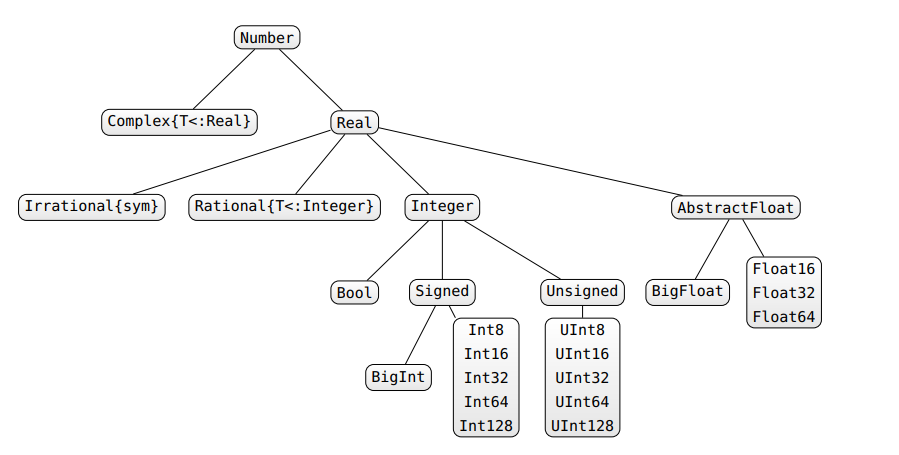
Hay varias formas de lidiar con las inestabilidades de tipo. En primer lugar, si le gusta algo como C / Fortran donde sus tipos se declaran y no pueden cambiar (lo que garantiza la estabilidad de los tipos), puede hacerlo en Julia:
local a::Int64 = 5
Esto hace a número entero de 64 bits, y si el código futuro intenta cambiarlo, se generará un mensaje de error (o se realizará la conversión correcta. Pero como la conversión no se redondeará automáticamente, lo más probable es que cause errores). Espolvéalos alrededor de tu código y obtendrás estabilidad de tipo, ala, C / Fortran . Una forma menos complicada de manejar esto es con declaraciones de tipo. Aquí pones la misma sintaxis en el otro lado del signo igual. Por ejemplo:
a = (b/c)::Float64
Parece decir: "calcule b / c y asegúrese de que la salida sea Float64. Si no lo está, intente realizar una conversión automática. Si la conversión no puede realizarse fácilmente, envíe un error". Colocar tales diseños lo ayudará a asegurarse de saber qué tipos están involucrados. Sin embargo, en algunos casos, la inestabilidad de tipo es necesaria. Por ejemplo, supongamos que desea tener un código confiable, pero el usuario le ofrece algo loco, como:
arr = Vector{Union{Int64,Float64}}(undef, 4) arr[1]=4 arr[2]=2.0 arr[3]=3.2 arr[4]=1
que es una matriz de enteros 4x1 y números de punto flotante. El tipo de elemento real para la matriz es Union {Int64, Float64} , que, como vimos anteriormente, no era estricto, lo que podría generar problemas. El compilador solo sabe que cada valor puede ser un número entero o un número de coma flotante, pero no qué elemento de qué tipo. Esto significa que es ingenuo hacer aritmética con esta matriz, por ejemplo:
function foo{T,N}(array::Array{T,N}) for i in eachindex(array) val = array[i] # do algorithm X on val end end
será lento ya que las operaciones serán encuadradas. Sin embargo, podemos utilizar el envío múltiple para ejecutar códigos de manera especializada. Esto se conoce como el uso de barreras funcionales. Por ejemplo:
function inner_foo{T<:Number}(val::T) # Do algorithm X on val end function foo2{T,N}(array::Array{T,N}) for i in eachindex(array) inner_foo(array[i]) end end
Tenga en cuenta que debido al envío múltiple, la llamada a inner_foo llama a un método específicamente compilado para números de coma flotante o un método especialmente compilado para enteros. Por lo tanto, puede poner un cálculo largo en inner_foo y aún así hacerlo funcionar bien, no inferior al tipo estricto que le proporciona la barrera funcional.
Por lo tanto, espero que vea que Julia ofrece una buena combinación de rendimiento de escritura fuerte y la comodidad de la escritura dinámica. Una buena programadora, Julia, tiene ambas opciones para maximizar la productividad y / o la productividad si es necesario.
Sorpresa 3: Eval funciona a nivel mundial

Una de las mayores fortalezas de Julia es su capacidad de metaprogramación. Esto le permite escribir fácilmente programas generadores de código, reduciendo efectivamente la cantidad de código que necesita escribir y mantener. Una macro es una función que se ejecuta en tiempo de compilación y (generalmente) escupe código. Por ejemplo:
macro defa() :(a=5) end
reemplazará cualquier instancia defa con el código a = 5 ( :(a = 5) es una expresión entre comillas . El código de Julia es expresiones y, por lo tanto, la metaprogramación es una colección de expresiones).
Puede usar esto para construir cualquier programa complejo de Julia que desee y ponerlo en una función como un tipo de atajo realmente inteligente. Sin embargo, a veces puede que necesite evaluar directamente el código generado. Julia le da una función de eval o macro @eval para hacer esto. En general, debe intentar evitar la eval , pero hay algunos códigos donde es necesario, por ejemplo, mi nueva biblioteca para transferir datos entre diferentes procesos para la programación paralela . , , :
@eval :(a=5)
(REPL). , / . Por ejemplo:
function testeval() @eval :(a=5) return 2a+5 end
, a REPL. , , :
function testeval() @eval :(a=5) b = a::Int64 return 2b+5 end
b — , , , , , . eval , , REPL .
4:
Julia , . : , .
, ? , , . Por ejemplo:
a = 2 + 3 + 4 + 5 + 6 + 7 +8 + 9 + 10+ 11+ 12+ 13 a
, 90, 27. ? a = 2 + 3 + 4 + 5 + 6 + 7 , a = 27 , +8 + 9 + 10+ 11+ 12+ 13 , , , :
a = 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10+ 11+ 12+ 13
90, . , .
. — , . rssdev10
. Por ejemplo:
x = rand(2,2) a = [cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi) -sin(2.*x[:,1]).*sin(2.*x[:,2])./(4)] b = [cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi) - sin(2.*x[:,1]).*sin(2.*x[:,2])./(4)]
, a b — , ! (2,2) , — (1-) 2. , , :
a = [1 -2] b = [1 - 2]
: 1 -2 . : 1-2 . - . :
a = [1 2 3 -4 2 -3 1 4]
2x4. , . : hcat :
a = hcat(cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi),-sin(2.*x[:,1]).*sin(2.*x[:,2])./(4))
!
№5: ,

(View) — () , ( ), .
, , . , . , .
— "". ""
a = [3;4;5] b = a b[1] = 1
, a — [1; 4; 5] , . . b a . , b = a b a . , , b , , ( b a ). , . , , :
a = rand(2,2) # Makes a random 2x2 matrix b = vec(a) # Makes a view to the 2x2 matrix which is a 1-dimensional array
b , b a , b . , , ( , ). . , . Por ejemplo:
c = a[1:2,1]
c a ). , , , , . , , :
d = @view a[1:2,1] e = view(a,1:2,1)
d , e — , d e a , , , reshape , .) , . Por ejemplo:
a[1:2,1] = [1;2]
a , a[1:2,1] view (a, 1:2,1) , , a . -? , :
b = copy(a)
, b a , , b a . a , copy! (B, a) , a a ( , b ). . , Vector {Vector} :
a = [ [1, 2, 3], [4, 5], [6, 7, 8, 9] ]
b = copy(a) b[1][1] = 10 a
3-element Array{Array{Int64,1},1}: [10, 2, 3] [4, 5] [6, 7, 8, 9]
, a[1][1] 10! ? copy a . a , b , b . , deepcopy :
b = deepcopy(a)
, . , , .
№6: , In-Place
MATLAB / Python / R . Julia , , , " ".
function f() x = [1;5;6] for i = 1:10 x = x + inner(x) end return x end function inner(x) return 2x end
, inner , , 2x . , . , - y , :
function f() x = [1;5;6] y = Vector{Int64}(3) for i = 1:10 inner(y,x) for i in 1:3 x[i] = x[i] + y[i] end copy!(y,x) end return x end function inner!(y,x) for i=1:3 y[i] = 2*x[i] end nothing end
. inner!(y, x) , y . y , y , , , inner! (y, x) ! ( ).
, inner!(y, x) . copy!(y, x) — , x y , . , , . : x y . , x + inner(x) , , , 11 . , .
, , , . - ( loop-fusion ). Julia v0.5 . ( ( broadcast ), f.(x) — , f x , , . f x , x = x + f. (x) . :
x .= x .+ f.(x)
.= , , ,
for i = 1:length(x) x[i] = x[i] + f(x[i]) end
, :
function f() x = [1;5;6] for i = 1:10 x .= x .+ inner.(x) end return x end function inner(x) return 2x end
MATLAB / R / Python , , , .
: ,
: , . , . , . , , . , .
- , C / Fortran , . - , , !
: ? , . , , ? [ , Javascript var x = 3 x , x = 3 x . ? , - Javascript!]