Los algoritmos para recomendaciones, predicciones de eventos o evaluaciones de riesgos son una solución de tendencia en bancos, compañías de seguros y muchos otros sectores empresariales. Por ejemplo, estos programas ayudan, basándose en el análisis de datos, a predecir cuándo un cliente devolverá un préstamo bancario, cuál será la demanda en el comercio minorista, cuál es la probabilidad de un evento asegurado o una salida de clientes en telecomunicaciones, etc. Para una empresa, esta es una valiosa oportunidad para optimizar sus gastos, aumentar la velocidad del trabajo y, en general, mejorar el servicio.
Sin embargo, los enfoques tradicionales como la clasificación y la regresión no son adecuados para construir tales programas. Consideremos este problema como un ejemplo de un caso dedicado a la predicción de episodios médicos: analizamos los matices en la naturaleza de los datos y los posibles enfoques para modelar, construir un modelo y analizar su calidad.
El desafío de predecir episodios médicos
La predicción de episodios se basa en un análisis de datos históricos. El conjunto de datos en este caso consta de dos partes. El primero son los datos sobre los servicios prestados previamente al paciente. Esta parte del conjunto de datos incluye datos sociodemográficos sobre el paciente, como la edad y el sexo, así como los diagnósticos que se le hicieron en diferentes momentos en la codificación ICD10-CM [1] y los procedimientos HCPCS realizados [2]. Estos datos forman secuencias en el tiempo que le permiten tener una idea de la condición del paciente en el momento de su interés. Para los modelos de capacitación, así como para trabajar en la producción, los datos personalizados son suficientes.
La segunda parte del conjunto de datos es una lista de episodios que ocurren para el paciente. Para cada episodio, indicamos su tipo y fecha de ocurrencia, así como el período de tiempo, los servicios incluidos y otra información. A partir de estos datos, se generan variables objetivo para la predicción.
El aspecto del tiempo es importante para resolver el problema: solo nos interesan los episodios que puedan surgir en el futuro cercano. Por otro lado, el conjunto de datos a nuestra disposición se recopiló durante un período limitado de tiempo, más allá del cual no hay datos. Por lo tanto, no podemos decir si los episodios ocurren fuera del período de observación, qué episodios son, en qué momento exacto surgen. Esta situación se llama censura correcta.
Del mismo modo, ocurre la censura izquierda: para algunos pacientes, un episodio puede comenzar a desarrollarse antes de lo que está disponible para nuestra observación. Para nosotros, se verá como un episodio que surgió sin ningún trasfondo.
Existe otro tipo de censura de datos: la interrupción de la observación (si el período de observación no se completa y el evento no ha ocurrido). Por ejemplo, debido a un paciente en movimiento, una falla en el sistema de recolección de datos, etc.
En la fig. 1 muestra esquemáticamente diferentes tipos de censura de datos. Todos ellos distorsionan las estadísticas y dificultan la construcción de un modelo.
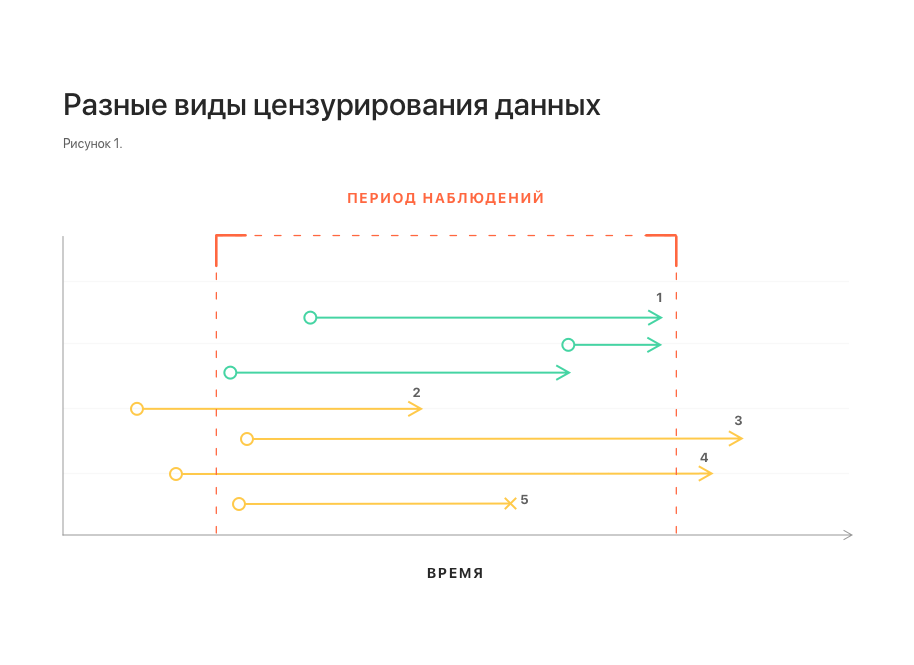Notas: 1 - observaciones sin censura; 2, 3 - censura izquierda y derecha, respectivamente; 4 - censura izquierda y derecha al mismo tiempo;
5 - interrupción de la observación.Otra característica importante del conjunto de datos está relacionada con la naturaleza del flujo de datos en la vida real. Algunos datos pueden llegar tarde, en cuyo caso no están disponibles en el momento de la predicción. Para tener en cuenta esta característica, es necesario complementar el conjunto de datos lanzando varios elementos desde la cola de cada secuencia.
Clasificación y regresión
Naturalmente, el primer pensamiento será reducir el problema a la conocida clasificación y regresión. Sin embargo, estos enfoques encuentran serias dificultades.
Por qué la regresión no nos conviene, queda claro a partir de los fenómenos considerados de la censura derecha e izquierda: la distribución del tiempo de ocurrencia de un episodio en el conjunto de datos puede cambiarse. Además, la magnitud y el hecho de la presencia de este sesgo no se pueden determinar utilizando el conjunto de datos en sí. El modelo construido puede mostrar resultados arbitrariamente buenos con cualquier enfoque de validación, pero esto, muy probablemente, no tendrá nada que ver con su idoneidad para pronosticar datos de producción.
Más prometedor, a primera vista, es un intento de reducir el problema a la clasificación: establecer un cierto período de tiempo y determinar el episodio que surgirá en este período. La principal dificultad aquí es la vinculación del intervalo de tiempo que nos interesa. Puede vincularse de manera confiable solo con el momento de la última actualización del historial del paciente. Al mismo tiempo, la solicitud de predecir el episodio generalmente no está vinculada al tiempo y puede llegar en cualquier momento, tanto dentro de este período (y luego se acorta el período de interés efectivo), como completamente más allá, y luego la predicción generalmente pierde su significado (ver Fig. 2) Esto naturalmente induce un aumento en el período de interés, lo que finalmente reduce el valor de la predicción de todos modos.
Notas: 1: actualiza el historial del paciente; 2 - la última actualización y el período de tiempo asociado a ella; 3, 4 - solicitudes de predicción de episodios recibidas durante este período. Se ve que el intervalo de predicción efectivo para ellos es menor; 5 - solicitud recibida fuera del intervalo. Para él, la predicción es imposible.Análisis de supervivencia
Como alternativa, podemos considerar el enfoque, en la literatura rusa, llamado análisis de supervivencia (análisis de supervivencia o análisis de tiempo hasta el evento) [3]. Esta es una familia de modelos diseñados específicamente para trabajar con datos censurados. Se basa en la aproximación de la función de riesgo (función de peligro, intensidad de ocurrencia de eventos), que estima la distribución de probabilidad de la ocurrencia de un evento a lo largo del tiempo. Este enfoque le permite tener en cuenta correctamente la presencia de diferentes tipos de censura.
Para resolver el problema, este enfoque también permite combinar ambos aspectos del problema en un modelo: determinar el tipo de episodio y predecir el momento de su ocurrencia. Para hacer esto, es suficiente construir un modelo separado para cada tipo de episodio, similar al enfoque de uno contra todos en la clasificación. Entonces, la aparición de un episodio no objetivo puede interpretarse como la exclusión de un objeto de la muestra observada sin la ocurrencia de un evento, que es otro tipo de censura de datos y el modelo también lo tiene en cuenta correctamente. Esta interpretación es correcta desde el punto de vista de la lógica empresarial: si un paciente se somete a una cirugía de cataratas, esto no excluye la aparición de otros episodios para él en el futuro.
Entre la familia de modelos para el análisis de supervivencia, se pueden distinguir dos variedades: analítica y de regresión. Los modelos analíticos son puramente descriptivos, están diseñados para toda la población, no tienen en cuenta las características de sus miembros individuales y, por lo tanto, solo pueden predecir la ocurrencia de un evento para algún miembro típico de la población. A diferencia del análisis, los modelos de regresión se construyen teniendo en cuenta las características de los miembros individuales de la población y permiten hacer pronósticos también para los miembros individuales teniendo en cuenta sus características. En este problema, fue esta variación la que se utilizó, o más bien, el modelo de riesgo proporcional de Cox (en adelante, CoxPH).
Regresión de supervivencia y cirugía de cataratas.
El enfoque más simple será similar a la regresión convencional: tome la expectativa matemática del momento del inicio del evento como la salida. Dado que CoxPH recibe datos como un vector numérico en la entrada, y nuestro conjunto de datos es, de hecho, una secuencia de códigos y procedimientos de diagnóstico (datos categóricos), se requiere una transformación de datos preliminar:
- Traducción de códigos en una representación incrustada utilizando el modelo GloVe previamente entrenado [4];
- Agregación de todos los códigos disponibles en el último período de la historia del paciente en un solo vector;
- Codificación directa del género del paciente y escala de edad.
Utilizamos los vectores de características obtenidos para el entrenamiento del modelo y su validación. El modelo resultante demuestra los siguientes valores de índice de concordancia (índice c o estadística c) [5]:
- 0,71 para la validación de 5 veces;
- 0,69 en la muestra pendiente.
Esto es comparable al nivel de 0.6-0.7 habitual para tales modelos [6].
Sin embargo, si observa el error absoluto medio entre el tiempo previsto esperado de ocurrencia del episodio y el real, resulta que el error es de 5 días. La razón de un error tan grande es que la optimización para el índice c garantiza solo el orden correcto de los valores: si un evento debe ocurrir antes que otro, entonces los valores pronosticados del tiempo esperado para los eventos serán uno menos que el otro, respectivamente. Además, no se hacen declaraciones con respecto a los valores predichos.
Otra posible variante del valor de salida del modelo es una tabla de valores de la función de riesgo en diferentes momentos. Esta opción tiene una estructura más compleja, es más difícil de interpretar que la anterior, pero al mismo tiempo proporciona más información.
Cambiar el formato de salida requiere una forma diferente de evaluar la calidad del modelo: debemos asegurarnos de que para los ejemplos positivos (cuando ocurre un episodio) el nivel de riesgo sea más alto que para los ejemplos negativos (cuando no ocurre un episodio). Para hacer esto, para cada distribución predicha de la función de riesgo en la muestra retrasada, pasaremos de la tabla de valores a un valor: el máximo. Habiendo contado los valores medios para ejemplos positivos y negativos, veremos que difieren de manera confiable: 0.13 versus 0.04, respectivamente.
Luego, usamos estos valores para construir la curva ROC y calcular el área debajo de ella: ROC AUC, que es 0.92, que es aceptable para el problema que se está resolviendo.
Conclusión
Por lo tanto, vimos que el análisis de supervivencia es el mejor enfoque para resolver el problema de predecir episodios médicos, teniendo en cuenta todos los matices del problema y los datos disponibles. Sin embargo, su aplicación implica un formato diferente de los datos de salida del modelo y un enfoque diferente para evaluar su calidad.
La aplicación del modelo CoxPH para predecir episodios de cirugía de cataratas nos permitió lograr indicadores de calidad del modelo aceptables. Se puede aplicar un enfoque similar a otros tipos de episodios, pero los indicadores de calidad específicos de los modelos solo se pueden evaluar directamente en el proceso de modelado.
Literatura
[1] CIE-10 Modificación clínica
en.wikipedia.org/wiki/ICD-10_Clinical_Modification[2] Sistema de codificación de procedimientos comunes de atención médica
en.wikipedia.org/wiki/Healthcare_Common_Procedure_Coding_System[3] Análisis de supervivencia
en.wikipedia.org/wiki/Survival_analysis[4] GloVe: Vectores globales para la representación de palabras
nlp.stanford.edu/projects/glove[5] Estadística C: definición, ejemplos, ponderación y significado
www.statisticshowto.datasciencecentral.com/c-statistic[6] VC Raykar y col. Sobre la clasificación en el análisis de supervivencia: límites en el índice de concordancia
papers.nips.cc/paper/3375-on-ranking-in-survival-analysis-bounds-on-the-concorda-index.pdf