IntroducciónUna gran cantidad de los problemas más diversos relacionados con casi todas las ramas más importantes de la física matemática y diseñados para responder preguntas técnicas tópicas están asociados con la aplicación de las funciones de Bessel.
Las funciones de Bessel se usan ampliamente para resolver problemas de acústica, radiofísica, hidrodinámica, problemas de física atómica y nuclear. Numerosas aplicaciones de las funciones de Bessel a la teoría de la conductividad térmica y la teoría de la elasticidad (problemas en las vibraciones de la placa, problemas de la teoría de la carcasa, problemas para determinar la concentración de tensión cerca de grietas).
Tal popularidad de las funciones de Bessel se explica por el hecho de que resolver ecuaciones de física matemática que contienen el operador de Laplace en coordenadas cilíndricas mediante el método clásico de separación de variables conduce a una ecuación diferencial ordinaria, que sirve para determinar estas funciones [1].
Las funciones de Bessel llevan el nombre del astrónomo alemán Friedrich Bessel, quien en 1824, al estudiar el movimiento de los planetas alrededor del sol, derivó las relaciones de recurrencia para las funciones de Bessel
Jv(x) recibido por enteros
v representación integral de una función
Jv(x) , demostró la existencia de innumerables ceros de función
J0(x) y compilé las primeras tablas para funciones
J1(x) y
J2(x) .
Sin embargo, por primera vez una de las funciones de Bessel
J0(x) Fue considerado en 1732 por Daniel Bernoulli en un trabajo dedicado a la oscilación de cadenas pesadas. D. Bernoulli encontró una expresión de función
J0(x) en forma de serie de potencia y notó (sin prueba) que la ecuación
J0(x)=0 tiene innumerables raíces válidas.
El siguiente trabajo, en el que se encuentran las funciones de Bessel, fue el trabajo de Leonardo Euler en 1738, dedicado al estudio de las vibraciones de una membrana circular. En este trabajo, L. Euler encontró enteros
v Expresión de la función de Bessel
Jv(x) en forma de una serie de poderes
x , y en trabajos posteriores extendió esta expresión al caso de valores de índice arbitrarios
v . Además, L. Euler demostró que para
v igual a un entero y medio, funciones
Jv(x) expresado a través de funciones elementales.
Señaló (sin evidencia) que con validez
v las funciones
Jv(x) tienen innumerables ceros reales y dieron una representación integral para
Jv(x) . Algunos investigadores creen que los principales resultados relacionados con las funciones de Bessel y sus aplicaciones en física matemática están relacionados con el nombre de L. Euler.
Estudiar la propiedad de las funciones de Bessel y al mismo tiempo dominar los métodos para resolver ecuaciones que se reducen a las funciones de Bessel, permite el programa distribuido libremente de SymPy de matemáticas simbólicas, la biblioteca de Python.
En el programa de matemática simbólica SymPy, se pueden construir gráficos de las funciones de Bessel del primer tipo de órdenes enteras utilizando la relación para la suma de una serie:
Jp(x)= sum inftym=0 fracx2m+p(−1)m22m+pm! Gamma(p+m+1)
Funciones de Bessel del primer tipofrom sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{p}(x)" p1=plot(besselj(0,x),(x,-20,20),line_color='b',title=' $'+st+ '$',show=False) p2=plot(besselj(1,x),(x,-20,20),line_color='g',show=False) p3=plot(besselj(2,x),(x,-20,20),line_color='r',show=False) p4=plot(besselj(3,x),(x,-20,20),line_color='c',show=False) p1.extend(p2) p1.extend(p3) p1.extend(p4) p1.show()
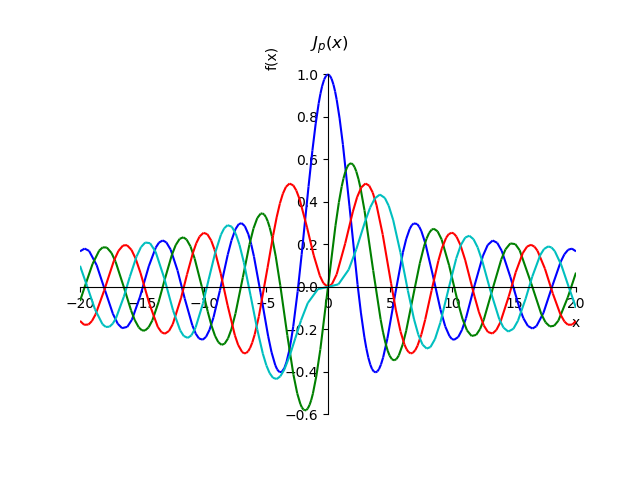
Usando la relación para la suma de una serie, podemos probar la propiedad de estas funciones para órdenes enteras
J1(x)=−J−1(x):
Propiedad de la función Bessel del primer tipo from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{1}(x)=-J_{-1}(x)" p1=plot(besselj(1,x),(x,-10,10),line_color='b',title=' $'+st+ '$',show=False) p2=plot(besselj(-1,x),(x,-10,10),line_color='r',show=False) p1.extend(p2) p1.show()

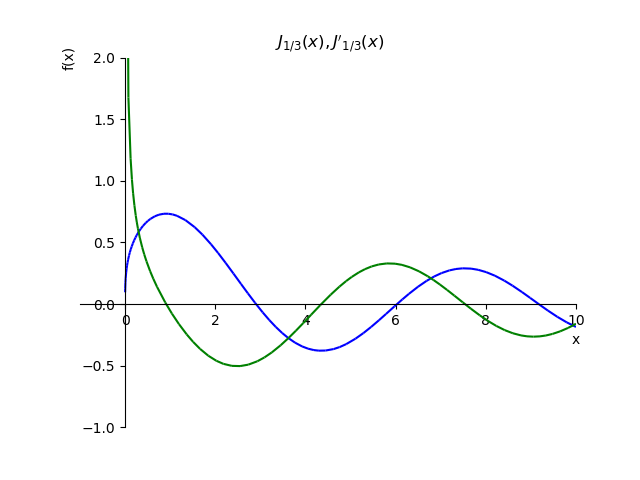
Para demostrar las condiciones de Cauchy, construimos una función
J1/3(x) y su derivada
fracdJ1/3(x)dx: :
Función de orden fraccional y su derivada from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{1/3}(x),J{}'_{1/3}(x)" p1=plot(besselj(1/3,x),(x,-1,10),line_color='b',title=' $'+st+ '$',ylim=(-1,2),show=False) def dbesselj(p,x): return diff(summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]),x) p2=plot(dbesselj(1/3,x),(x,-1,10),line_color='g',show=False) p1.extend(p2) p1.show()
Sin embargo, para cálculos prácticos, se utiliza el maravilloso módulo mpmath, que permite resolver numéricamente no solo ecuaciones con funciones de Bessel del primer y segundo tipo, incluidas las modificadas de todos los órdenes admisibles, sino también construir gráficos con escala automática.
Además, el módulo mpmath no requiere herramientas especiales para compartir matemática simbólica y numérica. La historia de la creación de este módulo y la posibilidad de su uso para la transformación inversa de Laplace que ya he considerado en la publicación [2]. Ahora continuamos la discusión sobre mpmath para trabajar con las funciones de Bessel [3].
Función de Bessel del primer tipo JN(x)mpmath.besselj (n, x, derivada = 0) : proporciona una función Bessel del primer tipo
Jn(x) . Las funciones
JN(x) es una solución a la siguiente ecuación diferencial:
x2y″+xy′+(x2−n2)y=0
Para todo lo positivo
n se comporta como un seno o coseno, multiplicado por un coeficiente que disminuye lentamente con
x rightarrow pm inftyFunción de Bessel del primer tipo
JN(x) es un caso especial de función hipergeométrica
oF1 :
Jn(x)= fracxn2n Gamma(n+1)oF1(n+1, fracx24)
La función de Bessel se puede diferenciar
m veces siempre que la derivada enésima no sea igual a cero:
fracdmdxmJn(x)
Función de Bessel del primer tipo
JN(x) para órdenes enteras positivas n = 0,1,2,3 - la solución de la ecuación de Bessel:
from mpmath import* j0 = lambda x: besselj(0,x) j1 = lambda x: besselj(1,x) j2 = lambda x: besselj(2,x) j3 = lambda x: besselj(3,x) plot([j0,j1,j2,j3],[0,14]

Función de Bessel del primer tipo
JN(x) en el plano complejo:
from sympy import* from mpmath import* cplot(lambda z: besselj(1,z), [-8,8], [-8,8], points=50000)
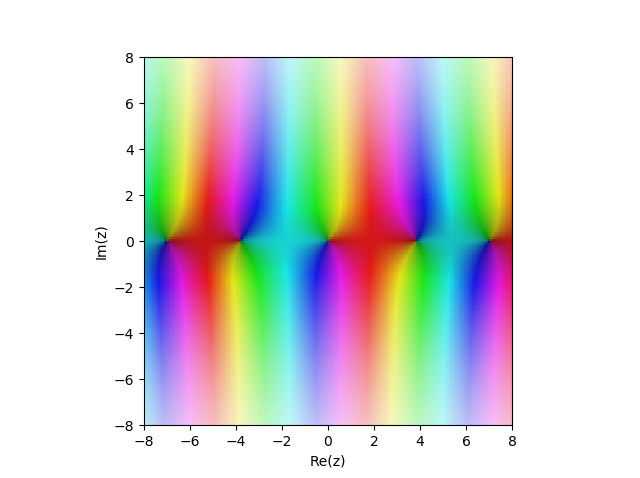
Ejemplos:
Función
besselj(N,x) proporciona un resultado con un número dado de dígitos
(mp.dps) después de la coma:
from mpmath import* mp.dps = 15; mp.pretty = True print(besselj(2, 1000)) nprint(besselj(4, 0.75)) nprint(besselj(2, 1000j)) mp.dps = 25 nprint( besselj(0.75j, 3+4j)) mp.dps = 50 nprint( besselj(1, pi))
Un argumento de función puede ser un gran número:
from mpmath import* mp.dps = 25 nprint( besselj(0, 10000)) nprint(besselj(0, 10**10)) nprint(besselj(2, 10**100)) nprint( besselj(2, 10**5*j))
Las funciones de Bessel del primer tipo satisfacen simetrías simples con respecto a
x=0 :
from sympy import* from mpmath import* mp.dps = 15 nprint([besselj(n,0) for n in range(5)]) nprint([besselj(n,pi) for n in range(5)]) nprint([besselj(n,-pi) for n in range(5)])
Las raíces no son periódicas, pero la distancia entre raíces sucesivas se aproxima asintóticamente
2π . Las funciones de Bessel del primer tipo tienen el siguiente código:
from mpmath import* print(quadosc(j0, [0, inf], period=2*pi)) print(quadosc(j1, [0, inf], period=2*pi))
Para
n=1/2 o
n=−1/2 La función de Bessel se reduce a una función trigonométrica:
from sympy import* from mpmath import* x = 10 print(besselj(0.5, x)) print(sqrt(2/(pi*x))*sin(x)) print(besselj(-0.5, x)) print(sqrt(2/(pi*x))*cos(x))
Los derivados de cualquier orden se pueden calcular,
las órdenes negativas corresponden a la integración :
from mpmath import* mp.dps = 25 print(besselj(0, 7.5, 1)) print(diff(lambda x: besselj(0,x), 7.5)) print(besselj(0, 7.5, 10)) print(diff(lambda x: besselj(0,x), 7.5, 10)) print(besselj(0,7.5,-1) - besselj(0,3.5,-1)) print(quad(j0, [3.5, 7.5]))
La diferenciación con el orden no entero da una derivada fraccional en el sentido de la integral diferencial de Riemann-Liouville, calculada utilizando la función
difint() :
from mpmath import* mp.dps = 15 print(besselj(1, 3.5, 0.75)) print(differint(lambda x: besselj(1, x), 3.5, 0.75))
Otras formas de llamar a la función Bessel del primer tipo de cero y primer orden
mpmath.j0 (x) - Calcula la función Bessel
J0(x) ;
mpmath.j1 (x) - Calcula la función Bessel
J1(x) ;
Funciones de Bessel del segundo tipo.bessely (n, x, derivada = 0) Calcula la función Bessel de segundo tipo a partir de la relación:
Yn(x)= fracJn(x)cos( pi cdotn)−J−n(x)sin( pi cdotn)
Para un entero
n La siguiente fórmula debe entenderse como el límite. La función de Bessel se puede diferenciar
m veces siempre que la derivada enésima no sea igual a cero:
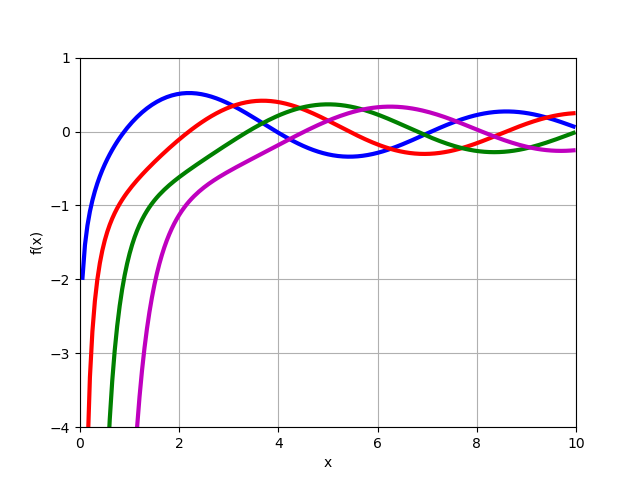
fracdmdxmYn(x)Función de Bessel del segundo tipo.
Yn(x) para órdenes positivas enteras
n=0,1,2,3 .
from sympy import* from mpmath import* y0 = lambda x: bessely(0,x) y1 = lambda x: bessely(1,x) y2 = lambda x: bessely(2,x) y3 = lambda x: bessely(3,x) plot([y0,y1,y2,y3],[0,10],[-4,1])
2ª función de Bessel amable
Yn(x) en el plano complejo
from sympy import* from mpmath import* cplot(lambda z: bessely(1,z), [-8,8], [-8,8], points=50000)
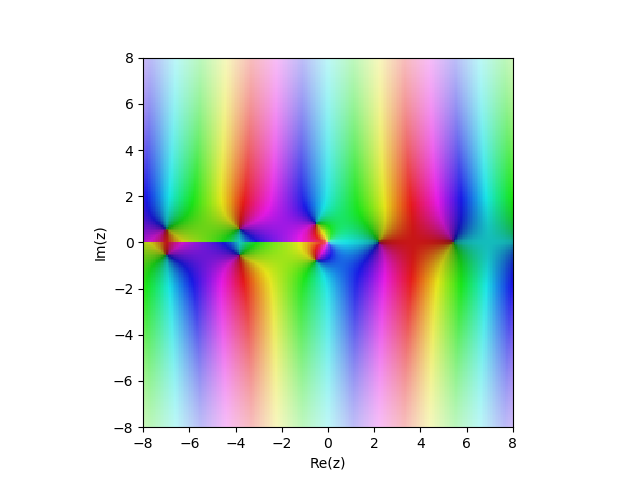
Ejemplos:
Algunos valores de funciones
Yn(x) :
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(0,0)) print(bessely(1,0)) print(bessely(2,0)) print(bessely(1, pi)) print(bessely(0.5, 3+4j))
Los argumentos pueden ser grandes:
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(0, 10000)) print(bessely(2.5, 10**50)) print(bessely(2.5, -10**50))
Los derivados de cualquier orden, incluidos los negativos, se pueden calcular:
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(2, 3.5, 1)) print(diff(lambda x: bessely(2, x), 3.5)) print(bessely(0.5, 3.5, 1)) print(diff(lambda x: bessely(0.5, x), 3.5)) print(diff(lambda x: bessely(2, x), 0.5, 10)) print(bessely(2, 0.5, 10)) print(bessely(2, 100.5, 100)) print(quad(lambda x: bessely(2,x), [1,3])) print(bessely(2,3,-1) - bessely(2,1,-1))
Función de Bessel modificada del primer tipo
mpmath.besseli(n, x, derivative=0)
besseli (n, x, derivada = 0) modificó la función de Bessel del primer tipo
In(x)= mathiti−nJn(ix)
fracdmdxmIn(x)
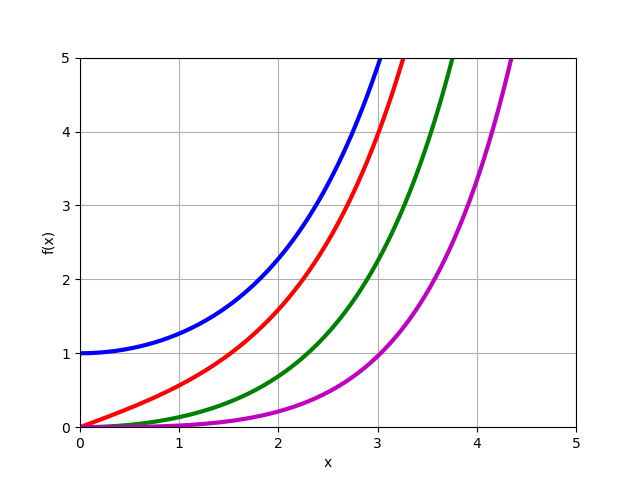
Función modificada de Bessel
In(x) para pedidos reales
n=0,1,2,3 :
from mpmath import* i0 = lambda x: besseli(0,x) i1 = lambda x: besseli(1,x) i2 = lambda x: besseli(2,x) i3 = lambda x: besseli(3,x) plot([i0,i1,i2,i3],[0,5],[0,5])
Función modificada de Bessel
In(x) en el plano complejo
from mpmath import* cplot(lambda z: besseli(1,z), [-8,8], [-8,8], points=50000)

Ejemplos:
Algunos significados
In(x) from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(0,0)) print(besseli(1,0)) print(besseli(0,1)) print(besseli(3.5, 2+3j))
Los argumentos pueden ser grandes:
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(2, 1000)) print(besseli(2, 10**10)) print(besseli(2, 6000+10000j))
Para los enteros n, se cumple la siguiente representación integral:
from mpmath import* mp.dps = 15; mp.pretty = True n = 3 x = 2.3 print(quad(lambda t: exp(x*cos(t))*cos(n*t), [0,pi])/pi) print(besseli(n,x))
Se pueden calcular derivados de cualquier orden:
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(2, 7.5, 1)) print(diff(lambda x: besseli(2,x), 7.5)) print(besseli(2, 7.5, 10)) print(diff(lambda x: besseli(2,x), 7.5, 10)) print(besseli(2,7.5,-1) - besseli(2,3.5,-1)) print(quad(lambda x: besseli(2,x), [3.5, 7.5]))
Funciones de Bessel modificadas del segundo tipo,
mpmath.besselk(n, x)
Besselk (n, x) funciones de Bessel de segundo tipo modificadas
Kn(x)= frac pi4 fracI−n(x)−In(x)sin( pi cdotn)
Para un entero
n Esta fórmula debe entenderse como un límite.
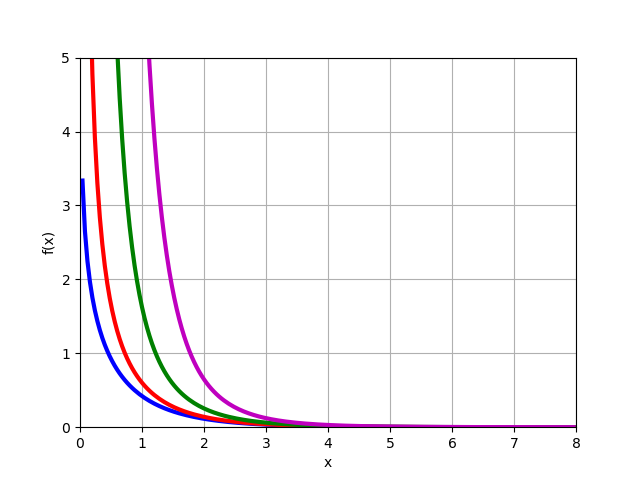
Función de Bessel modificada del segundo tipo
Kn(x) para material
n=0,1,2,3 :
from mpmath import* k0 = lambda x: besselk(0,x) k1 = lambda x: besselk(1,x) k2 = lambda x: besselk(2,x) k3 = lambda x: besselk(3,x) plot([k0,k1,k2,k3],[0,8],[0,5])
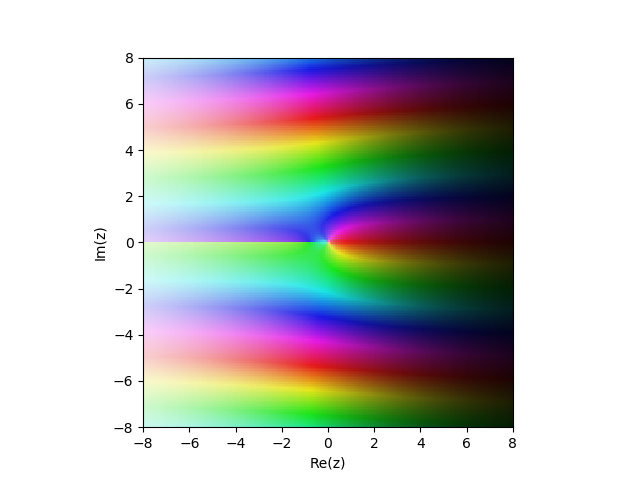
Función de Bessel modificada del segundo tipo
Kn(x)) en el plano complejo
from mpmath import* cplot(lambda z: besselk(1,z), [-8,8], [-8,8], points=50000)
Ejemplos:
Argumentos complicados y complejos:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselk(0,1)) print(besselk(0, -1)) print(besselk(3.5, 2+3j)) print(besselk(2+3j, 0.5))
Los argumentos son grandes números
from mpmath import * mp.dps = 25; mp.pretty = True print(besselk(0, 100)) print(besselk(1, 10**6)) print(besselk(1, 10**6*j)) print(besselk(4.5, fmul(10**50, j, exact=True)))
Características del comportamiento de una función en un punto.
x=0 :
from mpmath import * print(besselk(0,0)) print(besselk(1,0)) for n in range(-4, 5): print(besselk(n, '1e-1000'))
Función Bessel Ceros besseljzero() mpmath.besseljzero(v, m, derivative=0)
Por orden real
mathit nu geq0 y un entero positivo
m vuelve
j nu,m , el enésimo cero positivo de la función de Bessel del primer tipo
J nu(z) (ver
besselj () ). Alternativamente, con
derivada=1 da el primer cero primo no negativo
j′ nu,m de
J′ nu(z) . Designaciones de acuerdos de indexación con Abramowitz & Stegun y DLMF. Presta atención a un caso especial.
j′0,1=0 mientras que todos los otros ceros son positivos.
En realidad, solo se calculan los ceros simples (todos los ceros de las funciones de Bessel son simples, excepto cuando
z=0 ) y
j nu,m se convierte en una función monotónica de
nu y
m . Los ceros se alternan según las desigualdades:
j′ nu,k<j nu,k<j′ nu,k+1
j nu,1<j nu+1,2<j nu,2<j nu+1,2<j nu,3 cdots
Ejemplos:
Ceros a la izquierda de las funciones de Bessel
J0(z) ,
J1(z) ,
J2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,1)) print(besseljzero(0,2)) print(besseljzero(0,3)) print(besseljzero(1,1)) print(besseljzero(1,2)) print(besseljzero(1,3)) print(besseljzero(2,1)) print(besseljzero(2,2)) print(besseljzero(2,3))
Ceros a la izquierda de derivados de funciones de Bessel
J′0(z) ,
J′1(z) ,
J′2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,1,1)) print(besseljzero(0,2,1)) print(besseljzero(0,3,1)) print(besseljzero(1,1,1)) print(besseljzero(1,2,1)) print(besseljzero(1,3,1)) print(besseljzero(2,1,1)) print(besseljzero(2,2,1)) print(besseljzero(2,3,1))
Ceros con un índice grande:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,100)) print(besseljzero(0,1000)) print(besseljzero(0,10000)) print(besseljzero(5,100)) print(besseljzero(5,1000)) print(besseljzero(5,10000)) print(besseljzero(0,100,1)) print(besseljzero(0,1000,1)) print(besseljzero(0,10000,1))
Ceros de funciones con un orden grande:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(50,1)) print(besseljzero(50,2)) print(besseljzero(50,100)) print(besseljzero(50,1,1)) print(besseljzero(50,2,1)) print(besseljzero(50,100,1))
Ceros de funciones con orden fraccional:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0.5,1)) print(besseljzero(1.5,1)) print(besseljzero(2.25,4))
Y
J nu(z) . y
J′ nu(z) se pueden expresar como productos infinitos en sus ceros:
from mpmath import * mp.dps = 6; mp.pretty = True v,z = 2, mpf(1) nprint((z/2)**v/gamma(v+1) * \ nprod(lambda k: 1-(z/besseljzero(v,k))**2, [1,inf])) print(besselj(v,z)) nprint((z/2)**(v-1)/2/gamma(v) * \ nprod(lambda k: 1-(z/besseljzero(v,k,1))**2, [1,inf])) print(besselj(v,z,1))
besselyzero() mpmath.besselyzero(v, m, derivative=0)
Por orden real
mathit nu geq0 y un entero positivo
m vuelve
y nu,m ,
m , mth positivo cero del segundo tipo de función de Bessel
Y nu(z) (Ver
Bessely () ). Alternativamente, con
derivada=1 da el primer cero positivo
y′ nu,m de
Y′ nu(z) . Los ceros se alternan según las desigualdades:
y nu,k<y′ nu,k<y nu,k+1
y nu,1<y nu+1,2<y nu,2<y nu+1,2<y nu,3 cdots
Ejemplos:
Ceros a la izquierda de las funciones de Bessel
Y0(z) ,
Y1(z) ,
Y2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,1)) print(besselyzero(0,2)) print(besselyzero(0,3)) print(besselyzero(1,1)) print(besselyzero(1,2)) print(besselyzero(1,3)) print(besselyzero(2,1)) print(besselyzero(2,2)) print(besselyzero(2,3))
Ceros a la izquierda de derivados de funciones de Bessel
Y′0(z) ,
Y′1(z) ,
Y′2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,1,1)) print(besselyzero(0,2,1)) print(besselyzero(0,3,1)) print(besselyzero(1,1,1)) print(besselyzero(1,2,1)) print(besselyzero(1,3,1)) print(besselyzero(2,1,1)) print(besselyzero(2,2,1)) print(besselyzero(2,3,1))
Ceros con un índice grande:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,100)) print(besselyzero(0,1000)) print(besselyzero(0,10000)) print(besselyzero(5,100)) print(besselyzero(5,1000)) print(besselyzero(5,10000)) print(besselyzero(0,100,1)) print(besselyzero(0,1000,1)) print(besselyzero(0,10000,1))
Ceros de funciones con un orden grande:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(50,1)) print(besselyzero(50,2)) print(besselyzero(50,100)) print(besselyzero(50,1,1)) print(besselyzero(50,2,1)) print(besselyzero(50,100,1))
Ceros de funciones con orden fraccional:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0.5,1)) print(besselyzero(1.5,1)) print(besselyzero(2.25,4))
Aplicaciones de la función BesselLa importancia de las funciones de Bessel se debe no solo a la aparición frecuente de la ecuación de Bessel en las aplicaciones, sino también al hecho de que las soluciones de muchas otras ecuaciones diferenciales lineales de segundo orden se pueden expresar en términos de funciones de Bessel. Para ver cómo aparecen, comenzamos con la ecuación de orden de Bessel
p en forma de:
z2 fracd2wdz2+z fracdwdz+(z2−p2)w=0,(1)
y sustituir aquí
w=x− alpha,z=kx beta,(2)
Luego, usando (2) e introduciendo las constantes
A,B,C de la ecuación (1), obtenemos:
x2y″+Hachay′+(B+Cxq)y=0,(3)
A=1−2 alpha,B= alpha2− beta2p2,C= beta2k2,q=2 beta,(4)
De la ecuación (4) obtenemos:
\ left \ {\ begin {matrix} \ alpha = \ frac {1-A} {2}, \\ \ beta = \ frac {q} {2}, \\ k = \ frac {2 \ sqrt {C }} {q} \\ p = \ frac {\ sqrt {(1-A ^ {2} -4B}} {q} \\ \ end {matrix} \ right. (5)
Si
C>0 ,
q neq0 ,
(1−A)2 geqslant4B , entonces la solución general (para
x>0 ) de la ecuación (3) tiene la forma:
y(x)=x alpha left[c1Jp(kx beta)+c2J−p(kx beta) derecha](6)
donde:
alpha ,
beta ,
k se determinan a partir del sistema (5). Si
p Es un entero entonces
Jp necesita ser reemplazado por
Yp .
Doblado longitudinal de la columna verticalAhora consideraremos una tarea que es importante para aplicaciones prácticas. En esta tarea, se requiere determinar cuándo una columna vertical uniforme se dobla bajo su propio peso. Suponemos
x=0 en el extremo superior libre de la columna y
x=L>0 en su base; Suponemos que la base está rígidamente insertada (es decir, fija inmóvil) en la base (en el suelo), posiblemente en el hormigón.
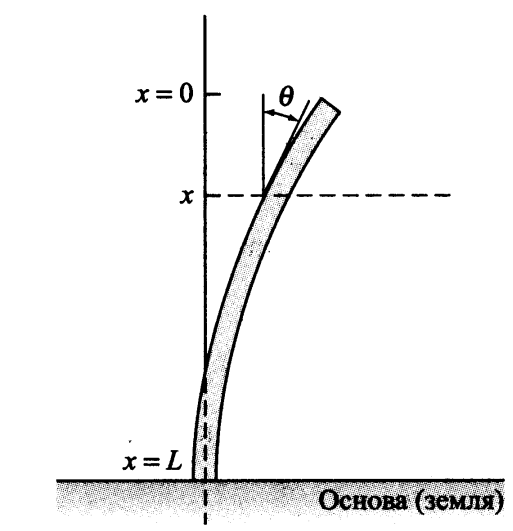
Denota la desviación angular de la columna en el punto
x a través de
theta(x) . De la teoría de la elasticidad bajo estas condiciones se deduce que:
EI fracd2 thetadx2+g rhox theta=0,(7)
donde
E - Módulo de Young del material de la columna,
I - momento de inercia de su sección transversal,
rho - densidad lineal de la columna y
g - aceleración gravitacional. Las condiciones de contorno son de la forma:
theta′(0)=0, theta(L)=0,(8)
Resolveremos el problema usando (7) y (8) con:
lambda= gamma2= fracg rhoEI(9)
Reescribimos (7) teniendo en cuenta (9) bajo la condición (8):
fracd2 thetadx2+ gamma2x theta=0; fracd thetadx=0, theta(L)=0.(10)
Una columna puede deformarse solo si hay una solución no trivial al problema (10); de lo contrario, la columna permanecerá en una posición no desviada de la vertical (es decir, físicamente incapaz de desviarse de la vertical).
La ecuación diferencial (10) es una ecuación de Airy. La ecuación (10) tiene la forma de la ecuación (3) para
A=B=0 ,
C= gamma2 ,
q=3 . Del sistema de ecuaciones (5) obtenemos
alpha= frac12 ,
beta= frac32 ,
k= frac23 gamma ,
p= frac13 .
Por lo tanto, la solución general tiene la forma:
theta(x)=x1/2 left[c1J1/3( frac23 gammax3/2)+c2J−1/3( frac23 gammax3/2) right].(11)
Para aplicar las condiciones iniciales, sustituimos
p= pm frac13 en
Jp= sum inftym=0 frac(−1)mm! Gamma(p+m+1) left( fracx2 right)2m+p(12)
Después de la transformación (12), teniendo en cuenta la solución (11), obtenemos:
theta(x)= fracc1 gamma1/331/3 Gamma(4/3) left(x− frac gamma2x412+ frac gamma4x7504− cdot cdot cdot right)++ fracc231/3 gamma1/3 Gamma( frac23) left(1− frac gamma2x36+ frac gamma4x6180− cdot cdot cdot right).(13)
Proporcionado en el punto de partida
theta′(0)=0 tenemos
c1=0 , entonces (11) toma la forma:
theta(x)=c2x1/2J−1/3( frac23 gammax3/2),(14)
Proporcionado en el punto final
theta(L)=0 , de (14) obtenemos:
J−1/3( frac23 gammaL3/2)=0(15)
Cabe señalar que las transformaciones (13), (14) no podrían hacerse si se construyeran las gráficas de funciones
J1/3(x),J−1/3(x) utilizando las capacidades consideradas del módulo mpmath:
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) f1=lambda x: besselj(1/3,x) plot([f,f1], [0, 15])
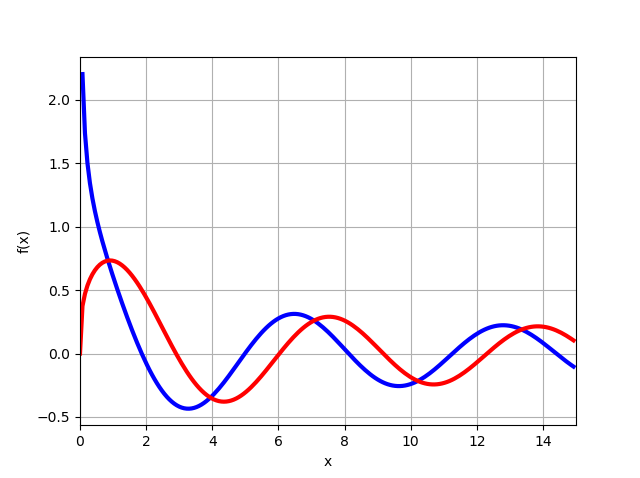
Del gráfico se deduce que para x = 0 la función
J1/3(0)=0 y teniendo en cuenta la solución (11), obtenemos inmediatamente la ecuación necesaria (15), solo queda encontrar z, como se mostrará a continuación.
Por lo tanto, la columna se deforma solo si
z= frac23 gammaL3/2 Es la raíz de la ecuación
J−1/3(z)=0 . Construye una función
J−1/3(z) en una tabla separada:
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) plot(f, [0, 15])

El gráfico muestra que la primera raíz es ligeramente menor que 2. Encuentra la raíz
z0 de la ecuación
J−1/3(z)=0 Puede, utilizando la función
findroot (f, z0) , aceptar, de acuerdo con el gráfico, el punto de búsqueda
x0=1 y seis decimales
mp.dps = 6 :
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) print("z0=%s"%findroot(f, 1)
Obtenemos:
z0=1.86635Calculamos la longitud crítica, por ejemplo, un asta de bandera, usando la fórmula (15):
Altura de asta de bandera para diferentes parámetros en la sección from numpy import* def LRr(R,r): E=2.9*10**11
Obtenemos:
8,47 m
10,25 m
Un asta hueca puede ser más alta que una sólida.
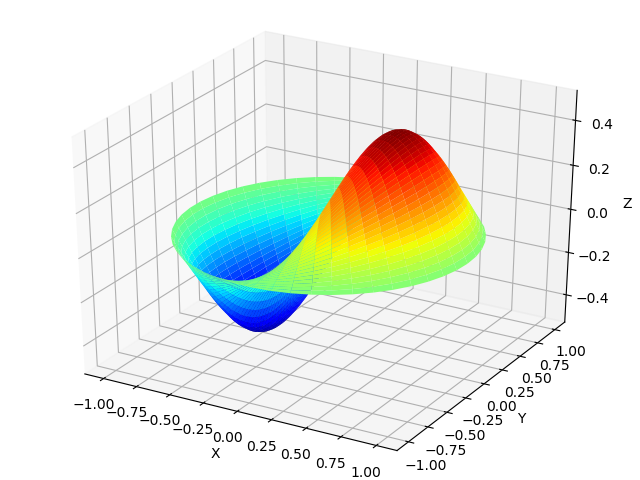
Propagación de ondas en una membrana delgada.
Una membrana delgada cuando las ondas de sonido golpean no solo oscila con la frecuencia de las ondas. La forma de las vibraciones de membrana se puede obtener en las funciones de Bessel de acuerdo con el siguiente listado, utilizando las fórmulas
besselj () y
besseljzero () :
Forma de onda de membrana from mpmath import* from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm def Membrana(r): mp.dps=25 return cos(0.5) * cos( theta) *float(besselj(1,r*besseljzero(1,1) ,0)) theta =linspace(0,2*pi,50) radius = linspace(0,1,50) x = array([r * cos(theta) for r in radius]) y = array([r * sin(theta) for r in radius]) z = array([Membrana(r) for r in radius]) fig = plt.figure("") ax = Axes3D(fig) ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel('X') ax.set_ylabel('Y') ax.set_zlabel('Z') plt.show()
Alternativa al módulo mpmath en funciones especiales de Bessel de la biblioteca SciPy
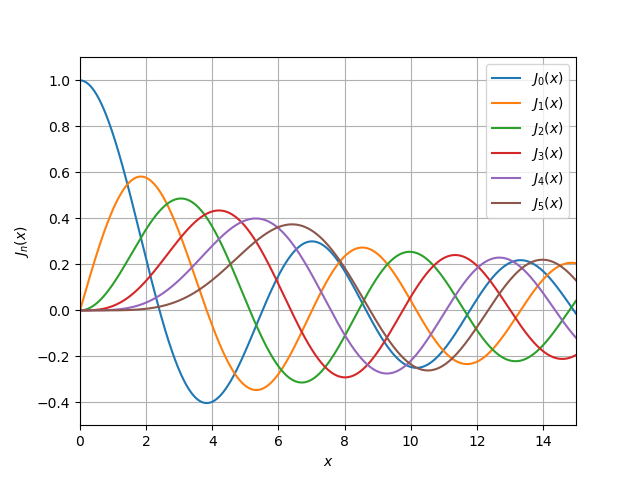
Sin profundizar en una discusión detallada de las funciones de Bessel de la biblioteca SciPy [4], daré solo dos listados para trazar funciones del primer y segundo tipo
jv (v, x) ,
yv (v, x) :
jv (v, x) import numpy as np import pylab as py import scipy.special as sp x = np.linspace(0, 15, 500000) for v in range(0, 6): py.plot(x, sp.jv(v, x)) py.xlim((0, 15)) py.ylim((-0.5, 1.1)) py.legend(('$J_{0}(x)$', '$ J_{1}(x)$', '$J_{2}(x)$', '$J_{3}(x)$', '$ J_{4}(x)$','$ J_{5}(x)$'), loc = 0) py.xlabel('$x$') py.ylabel('${J}_n(x)$') py.grid(True) py.show()
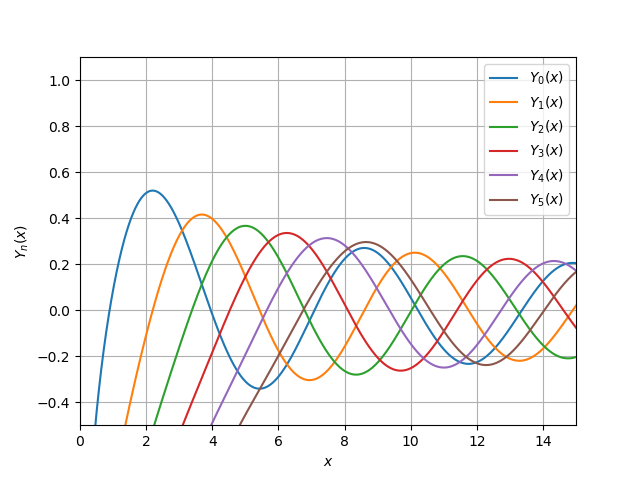
yv (v, x) import numpy as np import pylab as py import scipy.special as sp x = np.linspace(0, 15, 500000) for v in range(0, 6): py.plot(x, sp.yv(v, x)) py.xlim((0, 15)) py.ylim((-0.5, 1.1)) py.legend(('$Y_{0}(x)$', '$ Y_{1}(x)$', '$Y_{2}(x)$', '$Y_{3}(x)$', '$ Y_{4}(x)$','$ Y_{5}(x)$'), loc = 0) py.xlabel('$x$') py.ylabel('$Y_{n}(x)$') py.grid(True) py.show()
Conclusiones:
El artículo describe los conceptos básicos de trabajar con las funciones de Bessel usando las bibliotecas mpmath, sympy y scipy, y proporciona ejemplos del uso de funciones para resolver ecuaciones diferenciales. El artículo puede ser útil para estudiar las ecuaciones de la física matemática.
Referencias
1.
Funciones de Bessel2.
Usando la transformada inversa de Laplace para analizar los enlaces dinámicos de los sistemas de control3.
Funciones relacionadas con la función de Bessel4.
Funciones especiales (scipy.special).