El cuarto nivel del multiuniverso de Max Tegmark

Hace casi 10 años leí un artículo de Max Tegmark , un físico y filósofo brillante, y encontré en él las respuestas a muchas preguntas que me han atormentado toda mi vida. El artículo es sorprendente, durante dos meses tuve la impresión de tenerlo. Desafortunadamente, esto es Longrid, y también en inglés. Por lo tanto, decidí ni siquiera traducirlo: la traducción aún sería demasiado larga para Habr, pero al menos expuse la idea principal en el orden en que me parece lógico y eliminé detalles innecesarios (¡Max perdóname!)

Fórmulas y Equipaje

$$

$$A = bc$$

Que es esto Es poco probable que esta fórmula te diga algo. Y si lo escribo así:

$$

$$F = ma$$

Entonces reconocerás de inmediato la ley de Newton en él. Por supuesto, ambas fórmulas son equivalentes, solo estamos acostumbrados al hecho de que la fuerza se denota por F, masa m, además, queremos decir que la materia tiene lugar en un espacio tridimensional, que los cuerpos tienen coordenadas, etc. Es decir, la teoría tiene dos componentes: fórmulas y bla bla bla a su alrededor. Max llama al segundo componente equipaje verbal .

Considere el árbol de las teorías existentes:



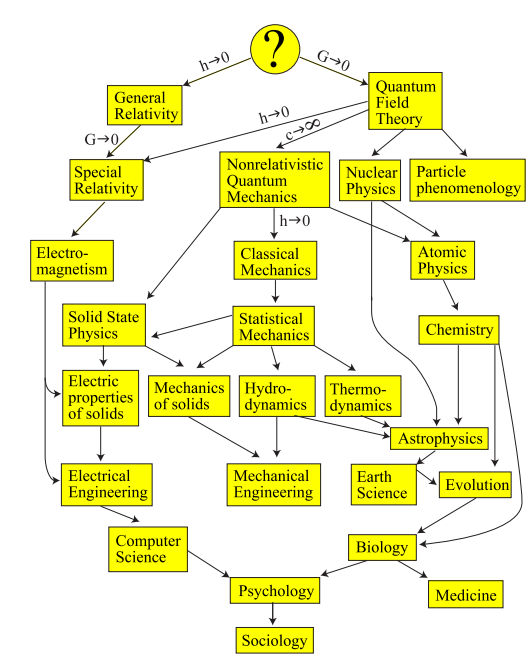
En el fondo está la sociología, donde casi no hay fórmulas, sino muchas palabras. Al subir, nos encontramos con matemáticas cada vez más complicadas. Pero con las palabras está empeorando cada vez más: intente averiguar a partir de un científico que se dedica a la física fundamental qué hora es. Es obvio para usted que el tiempo es una secuencia de eventos y fluye hacia adelante . Cuanto más sabes y más profundo vas, menos obvio se vuelve. La descripción de qué hora es, cada vez más colapsa al hecho de que el tiempo es la letra t , que está involucrada en tales ecuaciones.

Entonces Max nota que:
A medida que avanza a un nivel cada vez más fundamental, las matemáticas se vuelven más complejas y el equipaje comienza a degenerar más y más. En el límite, sugiere Max, el TOE (Theory of Everything - General Theory of Everything) no tiene equipaje . Entonces, TOE consiste solo en fórmulas .

Este es el primer ingrediente. Recuérdalo.

Física "Por el contrario"

¿Cómo es esto posible? La física está tratando de encontrar ecuaciones para nuestro mundo, basadas en observaciones y datos experimentales. Max sugiere mirar " Física desde cero " , " Física desde cero ", pregunta la ecuación, ¿qué tipo de mundo obtienes?

Podemos establecer las leyes del mundo ... bueno, por ejemplo, el juego "vida". ¿Podemos prescindir de una descripción verbal? ¿Cómo, por ejemplo, decir que el espacio de las celdas es bidimensional? A través de las ecuaciones, al indicar una ley de potencia, qué tan rápido crece el número de celdas no más allá de la distancia N. Otro ejemplo, las ecuaciones de la teoría de cuerdas convergen solo si la dimensión del espacio es 10, 11 o 26. Quizás, al principio, formular física parecerá axiomáticamente difícil, pero los matemáticos han tenido éxito. creando teorías axiomáticas (y mundos). Tomemos, por ejemplo, la axiomática de Peano . Estas son fórmulas puras, no explica qué es un "número", qué significa sumar o multiplicar.

Descripción vs equivalencia.

Que tenemos Tenemos (will) un TOE que describe TODO lo que existe.
Un segundo ... ¿Y qué significa "describir"? Por ejemplo, la mecánica describe el movimiento de los cuerpos. Pero sabemos que todo esto es posible gracias a una serie de simplificaciones: los cuerpos no son puntos materiales, hay resistencia al aire, fricción, etc. Hay fórmulas que describen la realidad, pero sabemos que el mundo real es diferente del ideal, descrito por las fórmulas.

Pero en el caso de TOE, esto no es así: cualquiera, absolutamente cualquier aspecto físico de la realidad se describe mediante fórmulas, o no es TOE. ¿Cuál es la diferencia entre teoría y realidad en este caso, si son absolutamente equivalentes?

Max argumenta que en el caso de TOE, las matemáticas no describen la realidad, y las matemáticas son la realidad . Si de repente no está de acuerdo, lo contrario significaría que hay ecuaciones con sus soluciones, existe exactamente el mismo mundo que está completamente sujeto a las fórmulas indicadas, pero también real . En este caso, las palabras " todavía real " son bagaje verbal en su forma pura, que abandonamos anteriormente, una anima de física tan moderna. Por lo tanto, nos vemos obligados a admitir que en el nivel fundamental, la física y las matemáticas son lo mismo.

Fórmulas y llamas

Max no fue el primero con tales ideas. Hawking mismo planteó la pregunta: " ¿Pero qué respira exactamente la llama en estas ecuaciones, creando el universo?" " ¿Qué es lo que respira fuego en las ecuaciones y crea un universo para que lo describan?"



Si dijéramos que nuestro universo es especial porque existe , volveríamos a dar un paso atrás hacia el concepto de anima sola. No, nada sopla la llama en nuestras fórmulas. Sería extraño que todos los sistemas axiomáticos de las matemáticas se dividieran en dos clases desiguales: sistemas para los que existen universos y sistemas desafortunados. Esto contradice toda la hipótesis del universo matemático.

Todo esto puede explicarse solo de esta manera: si no hay anima sola, entonces todos los sistemas axiomáticos son iguales y el universo corresponde a cada sistema axiomático. Sí, la mayoría de los sistemas son triviales, y quizás la mayoría de los axiomáticos no dan la oportunidad de desarrollar (es decir, aparecer en soluciones) sistemas complejos, no triviales y, especialmente, la vida.

"Física viceversa" todavía está esperando a sus futuros investigadores. Me gustaría mucho averiguar si nuestro universo es el más simple de aquellos donde la vida inteligente es posible o no.

Respuestas a algunas preguntas.

Curiosamente, después del primer paso (TOU no tiene equipaje), se forzaron el segundo paso (las matemáticas y la física son lo mismo) y el tercer paso (cada axiomática crea un universo). Así de lejos llegamos.

¿Y por qué existe el universo?
Respuesta: porque puede existir.

¿Cuándo surgieron estas estructuras y por qué surgieron?

Las estructuras matemáticas no existen en el tiempo y el espacio. Solo existen.

¿Somos una emulación?

No Para la existencia de estructuras matemáticas, no se necesita ninguna máquina para "contarlas". El número 19 es simple, independientemente de si hay una computadora o no que todo el tiempo trata de dividirla en un ciclo, buscando simplicidad

¿Y esto es generalmente como ciencia o fantasías?

¿Cómo podemos postular algo que no podemos verificar fundamentalmente? Max espera esta crítica. De hecho, esta no es la primera vez que hacemos esto. Hace tiempo que estamos acostumbrados al concepto del multiverso.



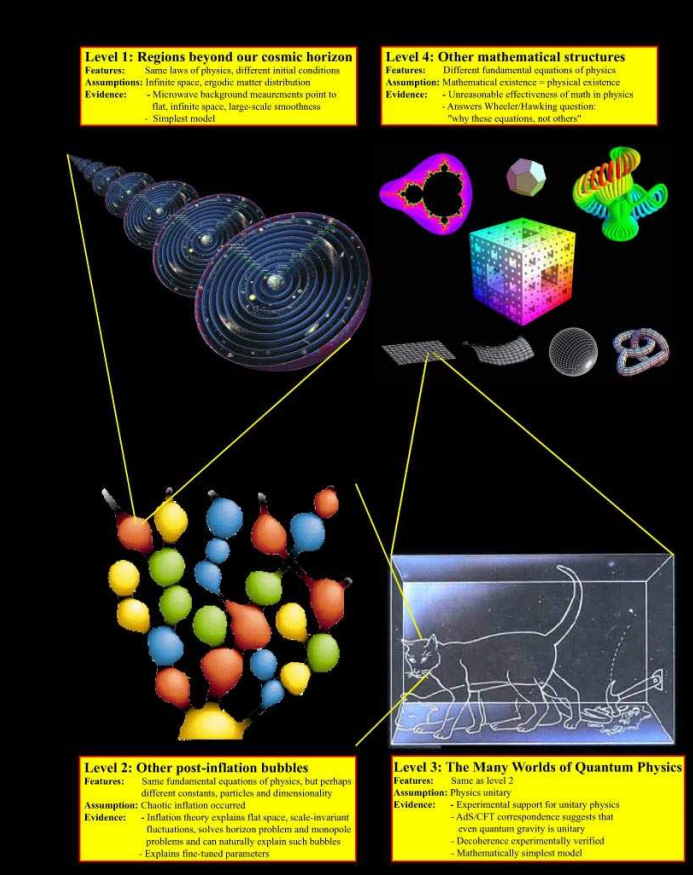En el nivel 1, estamos hablando de áreas del universo que se están alejando tan rápidamente de nosotros debido a la expansión que nunca más se conectarán causalmente con nosotros. Sin embargo, ningún cosmólogo se volverá loco para decir que no hay nada allí, porque no podemos volar allí.

En el nivel 2, estamos hablando de otras "burbujas" en la teoría de la inflación eterna, donde, tal vez, bajo las mismas leyes de la física, otras condiciones iniciales y otras constantes físicas

El nivel 3 está formado por los universos alternativos del multiverso tal como los interpreta Everett . Este será un artículo separado.



Nos vemos obligados a aceptar la existencia del nivel 4 , correspondiente a otros universos matemáticos que todavía tenemos que estudiar (teóricamente).