Desarrollar un hexápodo desde cero (parte 4) - trayectorias y secuencias matemáticas

Hola a todos! El desarrollo del hexápodo ha ido un paso más allá. Esta vez, se implementan y prueban las trayectorias del movimiento de las extremidades, la siguiente parte de las matemáticas del movimiento. En este artículo hablaré sobre estas trayectorias y secuencias básicas para el movimiento. Espero que sea interesante.

Etapas de desarrollo:
Parte 1 - Diseño
Parte 2 - montaje
Parte 3 - Cinemática
Parte 4 - trayectorias y secuencias matemáticas
Parte 5 - Electrónica
Parte 6: transición a la impresión 3D
Parte 7 - nuevo alojamiento, software de aplicación y protocolos de comunicación

Trayectorias

La esencia de este mecanismo es que cuando establece dos puntos, puede elegir la trayectoria de la extremidad. Al moverse de un punto a otro, las coordenadas cambiarán de acuerdo con ciertas ecuaciones paramétricas. El mecanismo resultó ser bastante poderoso y le permite obtener curvas interesantes para el movimiento. También implementa el suavizado de movimientos al cambiar el paso del parámetro t: cuanto más pequeño es el paso, más puntos intermedios habrá, menor será la velocidad y mayor será la suavidad del movimiento.

El procedimiento para establecer los parámetros de la trayectoria en algunos lugares es un poco incomprensible y puede confundirse en él. La dificultad radica en el hecho de que al establecer las coordenadas de los puntos inicial y final, las coordenadas de los puntos reales en el espacio no siempre se establecen, es decir. Algunas coordenadas establecen los parámetros de la trayectoria. Tuve que escribir un programa que muestra una ruta determinada y al mismo tiempo comprueba la accesibilidad de cada punto de la ruta.

El controlador admite las siguientes rutas de movimiento:

1. XYZ_LINAR es la más simple de todas las trayectorias. La trayectoria se utiliza al avanzar, retroceder, subir y bajar. Todas las coordenadas cambian linealmente y se calculan de la siguiente manera:
   
   

   x = t * (x1 - x0) / 180.0f + x0; y = t * (y1 - y0) / 180.0f + y0; z = t * (z1 - z0) / 180.0f + z0; 

   
   Aquí entendemos que no hay problemas. Las coordenadas especifican los ángulos paralelepípedos y coinciden con las coordenadas reales. El movimiento ocurre a lo largo de la diagonal de la caja.
   
   
   Visualización de trayectoria

   
   
   
   
   
   
2. YZ_ARC_Y_LINEAR : esta trayectoria le permite implementar movimiento a lo largo de un arco. La trayectoria se usa al girar, cuando necesitas mover una extremidad en el suelo. Las coordenadas se calculan de la siguiente manera:
   
   

    float R = sqrt(x0 * x0 + z0 * z0); float atan0 = RAD_TO_DEG(atan2(x0, z0)); float atan1 = RAD_TO_DEG(atan2(x1, z1)); float t_mapped_rad = DEG_TO_RAD(t * (atan1 - atan0) / 180.0f + atan0); x = R * sin(t_mapped_rad); // Circle Y y = t * (y1 - y0) / 180.0f + y0; z = R * cos(t_mapped_rad); // Circle X 

   
   Aquí es donde comienza la diversión. Las coordenadas especifican la dirección de los rayos para limitar el arco y pueden no coincidir con las coordenadas reales. Los rayos están en el mismo plano, mientras que el radio del círculo es igual a la longitud del vector hasta el punto de partida.
   
   
   Visualización de trayectoria

   
   
   
   
   
   
3. XZ_ARC_Y_SINUS : esta trayectoria también le permite implementar movimiento a lo largo de un arco, pero más complejo que YZ_ARC_Y_LINEAR. La trayectoria se usa al girar, cuando necesitas mover una extremidad por el aire. Las coordenadas se calculan de la siguiente manera:
   
   

    float R = sqrt(x0 * x0 + z0 * z0); float atan0 = RAD_TO_DEG(atan2(x0, z0)); float atan1 = RAD_TO_DEG(atan2(x1, z1)); float t_mapped_rad = DEG_TO_RAD(t * (atan1 - atan0) / 180.0f + atan0); x = R * sin(t_mapped_rad); // circle Y y = (y1 - y0) * sin(DEG_TO_RAD(t)) + y0; z = R * cos(t_mapped_rad); // circle X 

   
   La diversión continúa. Las coordenadas también especifican la dirección de los rayos para limitar el arco, pero NO coinciden con las coordenadas reales. La coordenada Y del punto objetivo establece la altura del seno.
   
   
   Visualización de trayectoria

   
   
   
   
4. XZ_ELLIPTICAL_Y_SINUS : esta trayectoria le permite implementar movimiento a lo largo de una elipse. La trayectoria se usa cuando se mueve hacia adelante y hacia atrás, cuando necesita mover una extremidad por el aire. Esta trayectoria es una complicación de XZ_ARC_Y_SINUS y se necesitaba solo debido a la marcha fea visual cuando se usa XZ_ARC_Y_SINUS (las piernas se extienden demasiado). Las coordenadas se calculan de la siguiente manera:
   
   

    float a = (z1 - z0) / 2.0f; float b = (x1 - x0); float c = (y1 - y0); x = b * sin(DEG_TO_RAD(180.0f - t)) + x0; // circle Y y = c * sin(DEG_TO_RAD(t)) + y0; z = a * cos(DEG_TO_RAD(180.0f - t)) + z0 + a; 

   
   Las coordenadas especifican los ángulos paralelepípedos y NO coinciden con las coordenadas reales. El movimiento se produce desde las esquinas inferiores de la caja, ubicadas en el mismo plano que tocando la parte superior de su parte. Es mejor mirar la imagen en el spoiler, no sé cómo describirla brevemente en palabras.
   
   
   Visualización de trayectoria

   
   

Esto completa las matemáticas básicas del movimiento del hexápodo. En mi proyecto, este es un mínimo necesario para la implementación de casi cualquier movimiento.

Secuencias

Poco de teoría

Las secuencias son las acciones elementales que componen la marcha. Se dividen en cíclicos y no cíclicos.

• Las secuencias cíclicas se pueden realizar muchas veces y al final de cada ciclo deben devolver las extremidades a su posición original (movimiento y rotación);
• Las secuencias no cíclicas se realizan solo una vez (ascenso y descenso);

Cada secuencia tiene tres bloques de iteración: bloque de preparación, bloque principal, bloque de finalización.

• Bloque de entrenamiento: contiene iteraciones para mover las extremidades a la posición inicial de la secuencia. En mi caso, avanzar requiere colocar las piernas en una determinada posición antes de comenzar a moverse. Se ejecuta una vez tras la transición a la secuencia;
• Bloque principal: contiene la iteración principal de la secuencia. Se puede realizar cíclicamente;
• Finalización de bloque: contiene iteraciones para mover las extremidades a la posición base (la posición en la que se establecen las extremidades después de levantarlas);

La siguiente figura muestra la secuencia para avanzar.

• Los puntos rojos indican la posición inicial de las extremidades antes de comenzar a moverse
• Las líneas azules indican las trayectorias de la extremidad en el suelo.
• Las líneas negras indican las trayectorias de la extremidad en el aire.
• Las flechas indican la secuencia.

Las coordenadas de los puntos se seleccionan en función de la configuración de la carcasa. Elegí los puntos lo más cerca posible del cuerpo para reducir la longitud de la palanca. En un ciclo de la secuencia, el hexápodo se mueve 18 cm (en 1 ciclo se toman 2 pasos - 1 paso en 3 extremidades). Si aumenta la distancia, las extremidades comenzarán a adherirse entre sí. Este parámetro está limitado solo por la configuración del caso.


La secuencia está definida por dos puntos (1, 2) para cada miembro y se utilizan dos caminos: XYZ_LINEAR (líneas azules) y XZ_ELLIPTICAL_Y_SINUS (líneas negras). El punto 1 es utilizado por la trayectoria XZ_ELLIPTICAL_Y_SINUS para establecer la altura del seno y, en consecuencia, la altura a la que se eleva el pie. Los puntos 2 y 3 son puntos reales que alcanza una extremidad cuando se mueve.

La ubicación de los puntos depende solo de su imaginación y de las capacidades del hexápodo. Quizás todo resultó un poco complicado y hay una opción más simple, pero aparentemente aún no la he alcanzado.

Implementación

Ahora echemos un vistazo a la implementación de toda esta felicidad. Las estructuras con parámetros de secuencia son las siguientes:

 typedef struct { point_3d_t point_list[SUPPORT_LIMB_COUNT]; path_type_t path_list[SUPPORT_LIMB_COUNT]; uint32_t smooth_point_count; } sequence_iteration_t; typedef struct { bool is_sequence_looped; uint32_t main_sequence_begin; uint32_t finalize_sequence_begin; uint32_t total_iteration_count; sequence_iteration_t iteration_list[15]; sequence_id_t available_sequences[SUPPORT_SEQUENCE_COUNT]; } sequence_info_t; 

secuencia_iteración_t : contiene información sobre la iteración de la secuencia:

• lista_puntos: una matriz de puntos para cada miembro en formato XYZ;
• path_list: una serie de trayectorias para cada miembro;
• smooth_point_count: establece el número de puntos de ruta (paso de parámetro t);

secuencia_info_t - contiene información sobre la secuencia completa:

• is_sequence_looped - establece el tipo de secuencia: cíclica o no;
• main_sequence_begin: establece el índice inicial del bloque principal en la matriz iteration_list;
• finalize_sequence_begin: establece el índice inicial del bloque de finalización en la matriz iteration_list;
• total_iteration_count: establece el número de iteraciones en la secuencia;
• iteration_list: una matriz de iteraciones;
• available_sequences: establece la lista de secuencias disponibles para la transición de la actual (por ejemplo, no podemos comenzar a caminar sin antes levantarnos del piso);

NOTA: El índice del bloque de preparación no se indica intencionalmente; siempre se encuentra al comienzo de la matriz de iteración.

Desafortunadamente, no puedo proporcionar un código para determinar la secuencia aquí, porque Es bastante amplio y se ve terrible después de las transferencias. Acabo de dejar un enlace al archivo de definición aquí.

Esquema de procesamiento de movimiento

Vale la pena distinguir todos los círculos del infierno que atraviesa la secuencia en tiempo de ejecución. El esquema de procesamiento es el siguiente:

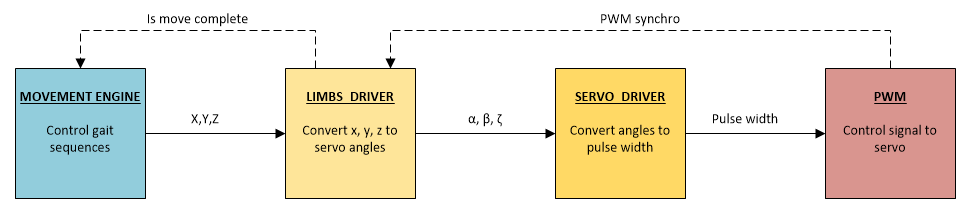
1. MOTOR DE MOVIMIENTO : organiza el procesamiento y el cambio entre secuencias. No se realizan cálculos allí. Si se simplifica, este módulo desliza el siguiente punto al módulo LIBMS DRIVER después de que se complete el procesamiento actual.
   Módulo de entrada: conjunto de coordenadas de puntos objetivo.
   Salida del módulo: punto objetivo para la iteración actual de la secuencia.
2. LIBMS DRIVER es el más complejo de todos los módulos. Aquí reina toda la matemática del movimiento: cinemática inversa, cálculos de trayectoria y suavizado de movimientos. Este módulo tiene una sincronización estricta con el módulo PWM. Los cálculos se llevan a cabo con una frecuencia de 150Hz, respectivamente, el pulso de control a los variadores también se suministra con una frecuencia de 150Hz.
   Entrada de módulo: coordenadas del punto objetivo.
   Salida del módulo: ángulos de rotación del servo.
3. SERVO CONDUCTOR . No tiene nada de especial, excepto un montón de parámetros para configurar y ajustar unidades.
   Entrada del módulo: ángulos de rotación del servo.
   Salida del módulo: control de ancho de pulso.
4. PWM DRIVER . Software controlador PWM para el control del variador. Aquí los pines se contraen en el momento adecuado. La variable de sincronización sincronizada PWM se incrementa cada período PWM.
   Entrada de módulo: ancho de pulso de control.
   Salida del módulo: pulsos en los pines de control.

Traté de hacer que los módulos fueran independientes entre sí y lo logré. Esto le permite insertar en este circuito cualquier módulo intermedio (por ejemplo, el módulo de adaptación al paisaje) y nada se romperá al mismo tiempo, mientras que la implementación ocurrirá con cambios mínimos en el código.

Últimas noticias y cangrejos de proyecto encontrados