Una leyenda urbana dice que el creador de bolsas de azúcar, palos, se ahorcó cuando se enteró de que los consumidores no los parten por la mitad en una taza, sino que arrancan suavemente la punta. Esto, por supuesto, no es así, pero si se sigue esta lógica, entonces un amante de la cerveza británica Guinness con el nombre de William Gosset no solo debería ahorcarse, sino que por su rotación en el ataúd ya debería perforar la Tierra hasta el centro. Y todo porque su invento icónico, publicado bajo el seudónimo de Estudiante , ha sido desastrosamente mal utilizado durante décadas.
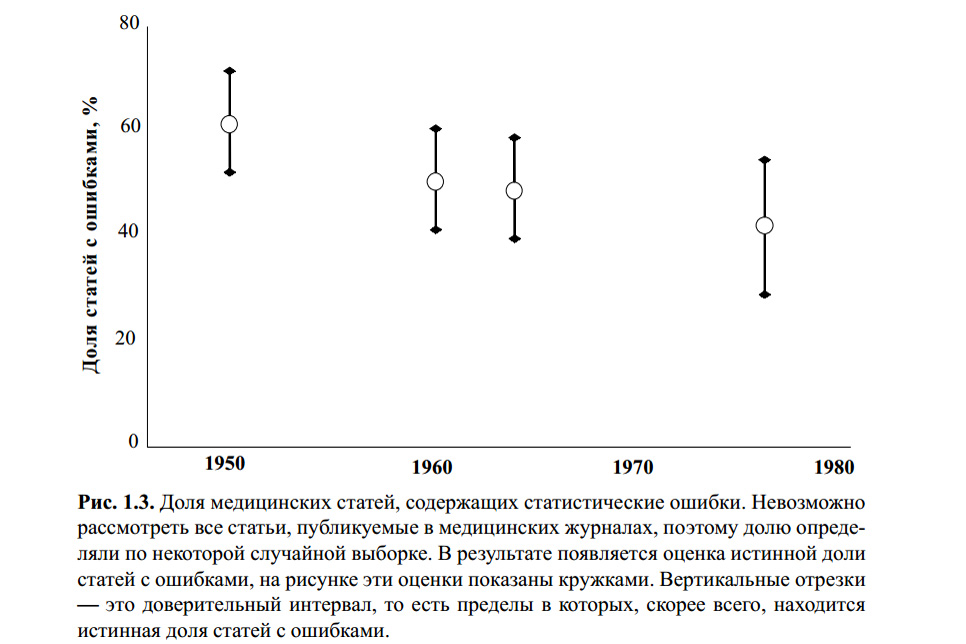
La figura de arriba es del libro de S. Glanz. Estadística biomédica. Por. del ingles - M., Practice, 1998 .-- 459 p. No sé si alguien verificó los errores estadísticos en los cálculos de este gráfico. Sin embargo, varios artículos modernos sobre el tema y mi propia experiencia indican que el criterio t de Student sigue siendo el más famoso y, por lo tanto, el más popular en uso, con o sin él.
La razón de esto es la educación superficial (los maestros estrictos enseñan que debe "verificar las estadísticas", de lo contrario, ¡uuuuuu!), La facilidad de uso (las tablas y las calculadoras en línea están disponibles en abundancia) y una reticencia banal a profundizar en el hecho de que "y así funciona". La mayoría de las personas que han utilizado este criterio al menos una vez en su trabajo final o incluso en trabajos científicos dirán algo como: "Bueno, comparamos 5 escolares enojados y 7 escolares-jugadores en términos de agresión, nuestro valor en la mesa se acerca a p = 0.05 y esto significa que los juegos son malos. Bueno, sí, no exactamente, pero con un 95% de probabilidad ". ¿Cuántos errores lógicos y metodológicos han cometido?
Los fundamentos
¿En qué se basa la prueba t de Student? La lógica se toma del teorema bayesiano, la base matemática es de la distribución gaussiana, la metodología se basa en el análisis de varianza:

donde el parámetro μ es la expectativa matemática (valor promedio) de la distribución, y el parámetro σ es la desviación estándar (σ ² es la varianza) de la distribución.
¿Qué es el análisis de varianza? Imagine una audiencia Habr, ordenada por la cantidad de personas de cada edad. Es probable que el número de personas por edad obedezca a la distribución normal, según la función de Gauss:
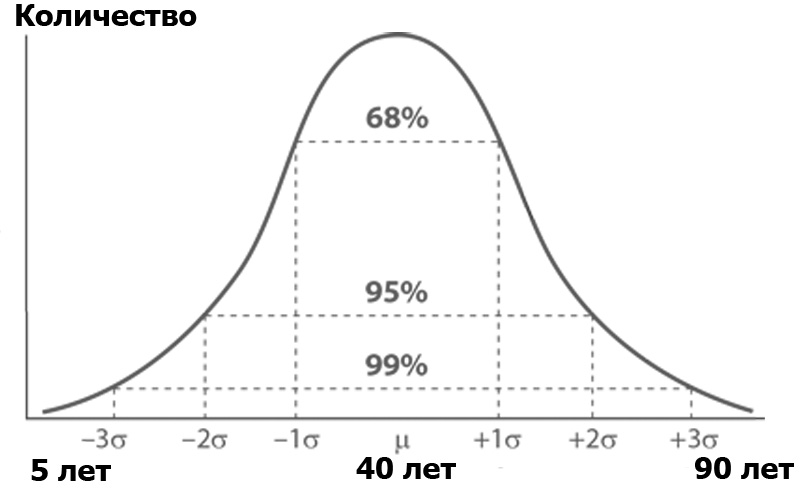
La distribución normal tiene una propiedad interesante: casi todos sus valores se encuentran en el límite de tres desviaciones estándar del valor promedio. ¿Y cuál es la desviación estándar? Esta es la raíz de la varianza. La dispersión , a su vez, es la suma de los cuadrados de la diferencia de todos los miembros de la población general y el valor promedio dividido por el número de estos miembros:
Es decir, cada valor se resta del promedio, se eleva al cuadrado para eliminar las desventajas, y luego se toma el promedio, se resume estúpidamente y se divide por el número de estos valores. El resultado es una medida de la dispersión promedio de valores en relación con la varianza promedio.
Imagine que seleccionamos dos muestras en esta población general : lectores del centro de criptomonedas y lectores del centro de Old Iron. Al hacer una muestra aleatoria , siempre obtenemos distribuciones cercanas a lo normal . Y ahora hemos conseguido un pequeño distribuidor dentro de nuestra población:
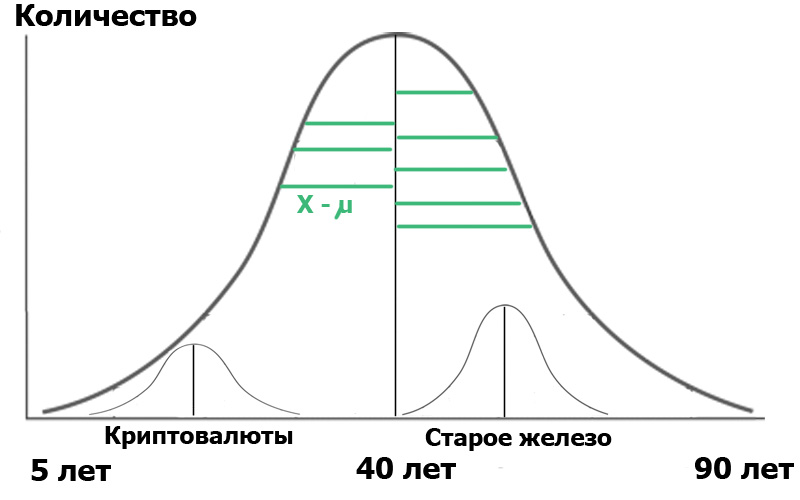
Para mayor claridad, mostré segmentos verdes: la distancia desde los puntos de distribución hasta el valor promedio. Si las longitudes de estos segmentos verdes son cuadradas, sumadas y promediadas, esta será la varianza.
Y ahora, atención. Podemos caracterizar a la población a través de estas dos pequeñas muestras. Por un lado, las variaciones de las muestras caracterizan la variación de toda la población. Por otro lado, ¡los valores promedio de las muestras también son números para los que se puede calcular la varianza! Entonces: tenemos el promedio de las varianzas de las muestras y la varianza de los valores promedio de las muestras.
Entonces podemos llevar a cabo un análisis de varianza, representándolo más o menos en forma de una fórmula lógica:
¿Qué nos dará la fórmula anterior? Muy simple En estadística, todo comienza con la "hipótesis nula", que puede formularse como "nos pareció", "todas las coincidencias son aleatorias", en sentido, y "no hay conexión entre los dos eventos observados", si es estrictamente. Entonces, en nuestro caso, la hipótesis nula sería la ausencia de diferencias significativas entre la distribución de edad de nuestros usuarios en dos centros. En el caso de la hipótesis nula, nuestro diagrama se verá así:
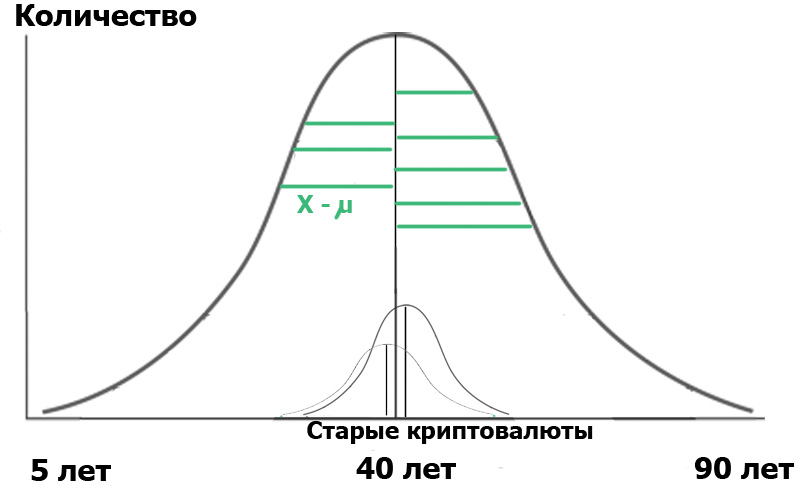
Esto significa que tanto las variaciones de las muestras como sus valores promedio son muy cercanos o iguales entre sí y, por lo tanto, en términos muy generales, nuestro criterio
Pero si las variaciones de las muestras son iguales, pero las edades de los usuarios son realmente muy diferentes, entonces el numerador (varianza de los valores promedio) será grande y F será mucho más que la unidad. Entonces el diagrama se verá más como en la figura anterior. ¿Y qué nos dará? Nada, si no prestas atención a la redacción: la hipótesis nula sería la ausencia de diferencias significativas .
Pero el significado ... lo establecemos nosotros mismos. Se denota como α y tiene el siguiente significado: el nivel de significancia es la probabilidad máxima aceptable de rechazar erróneamente la hipótesis nula . En otras palabras, consideraremos nuestro evento como una diferencia significativa entre un grupo y otro, solo si la probabilidad P de nuestro error es menor que α. Este es el notorio p <0.05, porque generalmente en la investigación biomédica el nivel de significancia se establece en 5%.
Bueno, entonces todo es simple. Dependiendo de α, existen valores críticos de F, comenzando con los cuales rechazamos la hipótesis nula. Se emiten en forma de tablas, que estamos tan acostumbrados a usar. Esto es para el análisis de varianza. ¿Y qué hay del estudiante?
Así dijo el estudiante
Y el criterio del estudiante es solo un caso especial de análisis de varianza. Nuevamente, no lo sobrecargaré con fórmulas que son fácilmente google, pero transmitiré la esencia:
Por lo tanto, toda esta larga explicación debía ser muy grosera y fluida, pero mostrar claramente en qué se basa el criterio t. Y, en consecuencia, a partir de cuáles de sus propiedades inherentes siguen directamente las limitaciones de su uso, en el que incluso los científicos profesionales a menudo cometen errores.
Propiedad uno: Normalidad de distribución.
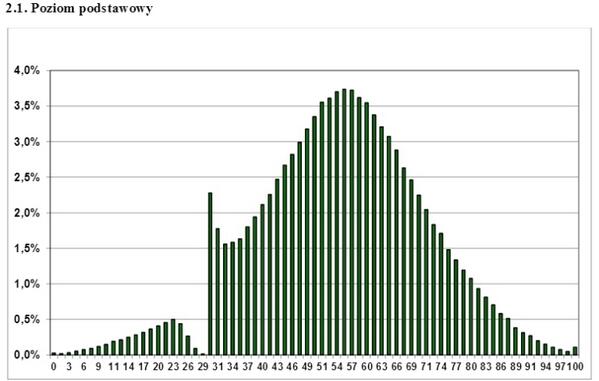
Este es un par de años como un gráfico de la distribución de los puntajes de los exámenes estatales polacos en Internet. ¿Qué conclusión se puede sacar de ella? ¿Que este examen no se aprueba solo completamente repelido Gopnik? ¿Qué maestros "alcanzan" a los estudiantes? No, solo uno: para una distribución diferente a la normal, no puede aplicar criterios de análisis paramétricos, como el de Estudiante. Si tiene un gráfico de distribución discreto, ondulado, ondulado, unilateral, olvídese del criterio t, no puede usarlo. Sin embargo, esto a veces es ignorado con éxito incluso por un trabajo científico serio.
¿Qué hacer en este caso? Utilice los llamados criterios de análisis no paramétricos. Implementan un enfoque diferente, a saber, los datos de clasificación, es decir, alejarse de los valores de cada uno de los puntos al rango asignado. Estos criterios son menos precisos que los paramétricos, pero al menos su uso es correcto, en contraste con el uso injustificado del criterio paramétrico en una población anormal. De estos criterios, el criterio U de Mann-Whitney es mejor conocido y, a menudo, se usa como criterio "para una muestra pequeña". Sí, le permite lidiar con muestras de hasta 5 puntos, pero esto, como debería estar claro, no es su objetivo principal.
La segunda propiedad: ¿recuerdas la fórmula? Los valores del criterio F cambiaron con la diferencia (varianza aumentada) de los valores promedio de las muestras . Pero el denominador, es decir, las variaciones en sí mismas, no debería cambiar. Por lo tanto, otro criterio de aplicabilidad debería ser la igualdad de las variaciones. El hecho de que este control se observe con menos frecuencia se dice, por ejemplo, aquí: Errores en el análisis estadístico de datos biomédicos. Leonov V.P. Revista Internacional de Práctica Médica, 2007, no. 2, págs . 19-35 .
Propiedad tres: Comparación de dos muestras. Les gusta usar el criterio t para comparar más de dos grupos. Como regla general, esto se hace de la siguiente manera: las diferencias entre el grupo A de B, B de C y A de C. se comparan en pares. Luego, en base a esto, se hace una cierta conclusión, que es absolutamente incorrecta. En este caso, surge el efecto de comparaciones múltiples.
Habiendo obtenido un valor suficientemente alto de t en cualquiera de las tres comparaciones, los investigadores informan que "P <0.05". Pero, de hecho, la probabilidad de error supera significativamente el 5%.
Por qué
Lo resolvemos: por ejemplo, el estudio adoptó un nivel de significación del 5%. Esto significa que la probabilidad máxima aceptable de rechazar erróneamente la hipótesis nula al comparar los grupos A y B es del 5%. Parece que todo es correcto? Pero el mismo error exacto ocurrirá en el caso de comparar los grupos B y C, y al comparar los grupos A y C, también. En consecuencia, la probabilidad de cometer un error en su conjunto con este tipo de evaluación no será del 5%, sino mucho más. En general, esta probabilidad es igual a
P ′ = 1 - (1 - 0.05) ^ k
donde k es el número de comparaciones.
Luego, en nuestro estudio, la probabilidad de cometer un error al rechazar la hipótesis nula es aproximadamente del 15%. Al comparar los cuatro grupos, el número de pares y, en consecuencia, las posibles comparaciones por pares es 6. Por lo tanto, con un nivel de significancia en cada una de las comparaciones de 0.05
la probabilidad de detectar por error una diferencia en al menos uno ya no es 0.05, sino 0.31.
Aún así, este error no es difícil de eliminar. Una forma es presentar la enmienda Bonferroni. La desigualdad de Bonferroni nos dice que si aplica los criterios k veces
con un nivel de significancia de α, entonces la probabilidad, en al menos un caso, de encontrar una diferencia donde no existe no excede el producto de k por α. Desde aquí:
α ′ <αk,
donde α 'es la probabilidad de al menos una vez confundir las diferencias. Entonces nuestro problema se resuelve de manera muy simple: necesitamos dividir nuestro nivel de significancia por la corrección de Bonferroni, es decir, por la multiplicidad de comparaciones. Para tres comparaciones, necesitamos tomar los valores correspondientes a α = 0.05 / 3 = 0.0167 de las tablas de prueba t. Repito: es muy simple, pero esta enmienda no puede ser ignorada. Por cierto, no debería dejarse llevar por esta enmienda, incluso después de dividir entre 8, los valores del criterio t son innecesariamente más estrictos.
Luego vienen las "pequeñas cosas" que muy a menudo no notan en absoluto. Deliberadamente no proporciono fórmulas aquí, para no reducir la legibilidad del texto, pero debe recordarse que los cálculos del criterio t varían para los siguientes casos:
Diferentes tamaños de dos muestras (en general, recuerde que en el caso general comparamos dos grupos usando la fórmula para el criterio de dos muestras);
Disponibilidad de muestras dependientes. Estos son casos en los que se miden datos de un paciente a diferentes intervalos de tiempo, datos de un grupo de animales antes y después del experimento, etc.
Finalmente, para que puedas imaginar el alcance total de lo que está sucediendo, proporcionaré datos más recientes sobre el uso incorrecto del criterio t. Los números son para 1998 y 2008 para varias revistas científicas chinas, y hablan por sí mismos. Realmente quiero que esto resulte ser más descuidado en diseño que datos científicos inexactos:
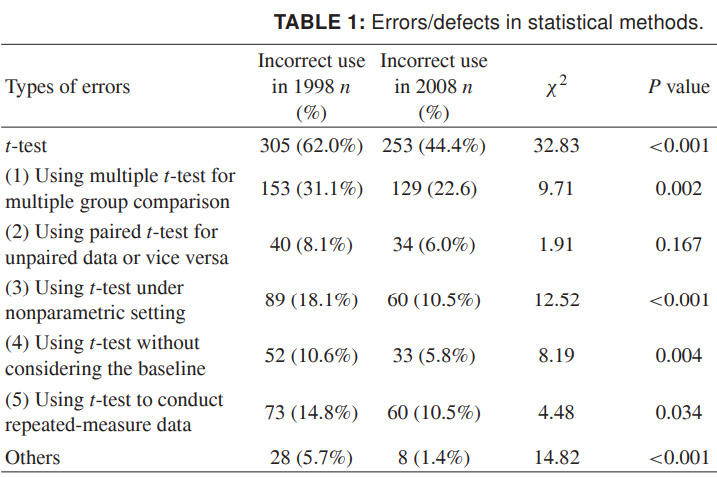
Fuente: Uso indebido de métodos estadísticos en 10 revistas médicas chinas líderes en 1998 y 2008. Shunquan Wu et al, The Scientific World Journal, 2011, 11, 2106–2114
Recuerde, la baja importancia de los resultados no es tan triste como un resultado falso. Es imposible llevar al pecado científico - conclusiones falsas - distorsionando los datos con estadísticas aplicadas incorrectamente.
Sobre la interpretación lógica, incluida la incorrecta, de los datos estadísticos, tal vez lo cuente por separado.
Léalo bien.