Despiértese por la mañana mientras canta tucanes, vea el pronóstico del tiempo y vea el mismo +28, póngase sus pantalones cortos favoritos y salga a caminar por la ciudad, aleje a los monos insolentes del basurero, camine por el callejón de las palmeras, siéntese en un banco frente al lago y alimente a los flamencos, recuerde la preparación en invierno y comprar otro pantalón corto. Para alguien, ese día no es inusual, pero para nosotros (me refiero a los habitantes de las regiones climáticas continentales) es realmente exótico. ¿Qué tienen que ver los flamencos y los tucanes con la física? Y a pesar del hecho de que lo exótico tampoco es ajeno a la física, se manifiesta en procesos, sustancias y fenómenos que de alguna manera difieren de la norma generalmente aceptada. Hoy hablaremos de uno de estos fenómenos: el segundo sonido que se encontró en el grafito ordinario. ¿Qué es tan exótico en él como lo han encontrado los científicos? ¿Deberíamos compartir su entusiasmo por el descubrimiento? Encontraremos las respuestas, dónde y generalmente, no, no en Google, sino en el informe del grupo de investigación. Vamos
Retiro teórico
El segundo sonido es un nombre bastante divertido para el fenómeno, que solo se refiere indirectamente al sonido en sí (está ligeramente en contacto con las mangas, por así decirlo). El segundo sonido es un fenómeno de mecánica cuántica en el que la transferencia de calor se realiza en forma de onda, en lugar de la difusión habitual. La palabra "sonido" está presente en el nombre de este proceso debido a la similitud de la propagación de la onda de calor con una propagación similar de las ondas de sonido.
Las ondas sonoras son fluctuaciones en la densidad de las moléculas de una sustancia, pero las ondas del segundo sonido ya son fluctuaciones en la densidad de las excitaciones térmicas en forma de partículas (fonones y
rotones * ).
Roton * es una cuasipartícula en superfluido 4 He (helio-4).
Se encontraron manifestaciones anteriores del segundo sonido en una lista bastante pequeña de sustancias y a temperaturas suficientemente bajas:
-
2 He - helio líquido (
superfluido * ) obtenido enfriando 4He por debajo de 2,1768 K;
-
4 He,
3 He, Bi (bismuto) a una temperatura de 1.2 ... 4.0 K y NaF (fluoruro de sodio) en estado sólido de agregación a una temperatura de 10 ... 20 K.
La superfluidez * es una propiedad de un fluido con viscosidad cero, lo que le permite fluir sin pérdida de energía cinética. En otras palabras, dicha sustancia (líquido cuántico) a temperaturas cercanas al cero absoluto puede pasar a través de agujeros y capilares muy estrechos sin fricción.
Sin embargo, los científicos no dejaron de buscar un segundo sonido en otras sustancias. La búsqueda arrojó resultados: se encontraron signos de un segundo sonido en el grafito ordinario a temperaturas superiores a 100 K.
En su estudio, los científicos utilizaron mediciones ópticas de transferencia de calor en grafito con una escala de longitud de 5-20 micras. Los resultados de observación son completamente comparables con los cálculos realizados anteriormente y teóricamente indican la presencia de un segundo sonido a una escala de ~ 1 μm a altas temperaturas (hasta temperatura ambiente).
Los investigadores nos recuerdan que en los sólidos no metálicos ordinarios, el calor se transfiere mediante vibraciones reticulares o
fonones * (que no debe confundirse con los fotones). En un cristal ideal (prácticamente) a una temperatura de aproximadamente 10 K, los fonones pueden propagarse a distancias microscópicas sin dispersión, y esto conduce a la transferencia de calor balístico.
Phonon * es un cuanto del movimiento vibratorio de un átomo de cristal.
A temperatura ambiente, la longitud promedio de transferencia de calor en el fonón es bastante pequeña debido a las altas velocidades de dispersión de fonón-fonón, por lo tanto, el calor se propaga debido a la difusión a distancias macroscópicas.
El segundo sonido, como fenómeno, se encuentra en algún lugar entre la transferencia de calor balístico y difusivo. Este modo intermedio se llama fonodhidrodinámica. En tal situación, la dispersión normal de fonón-fonón ocurre con mucha más frecuencia, en la cual se retiene el impulso de fonón reducido total, y
es menos probable que ocurra
el proceso de transferencia * .
Procesos de transferencia * : cuando las cuasipartículas chocan en cristales y la ley de conservación del momento se realiza hasta el vector de red recíproca. Sin embargo, la dispersión normal por sí sola no es suficiente para dispersar el flujo de calor y devolver la red al estado de equilibrio térmico. En cambio, la población de fonones se relaja con una distribución de Bose-Einstein "sesgada", caracterizada por una velocidad de deriva distinta de cero, que es comparable al flujo de moléculas en los gases. Esto permite que las ondas térmicas (ondas de densidad de fonones) se propaguen a una velocidad inferior a la velocidad del sonido.
Resultados de la investigación
En preparación para los experimentos reales, los científicos hicieron cálculos y se familiarizaron con algunas predicciones teóricas hechas anteriormente. Descubrieron que debería producirse un segundo sonido en el intervalo de tiempo entre la dispersión normal y el sobreimpulso (τ
N <t <τ
U ). De acuerdo con las predicciones teóricas, se estableció la escala de nanosegundos del experimento para el grafeno. Y esto complica el proceso de investigación debido a la incapacidad de usar sensores de temperatura convencionales para determinar la transferencia de calor. Por lo tanto, los científicos recurrieron a los láseres en busca de ayuda. Más precisamente, se utilizó el método de rejillas térmicas de transición (
1A ) cuando dos pulsos láser cortos (60 ps) se cruzan en la superficie de la muestra.
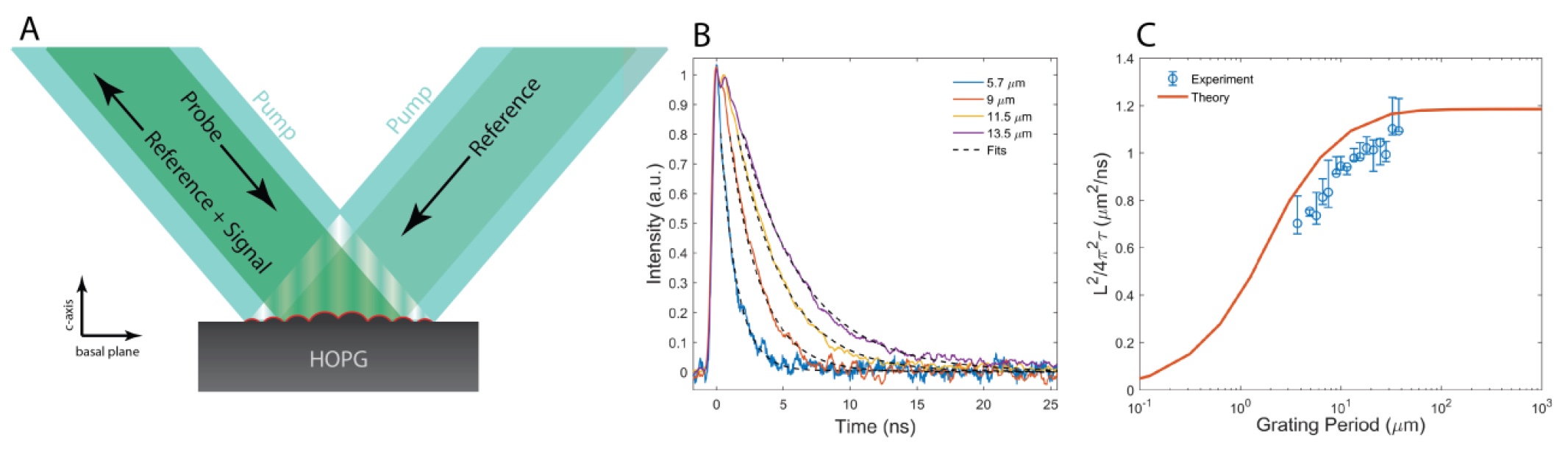Imagen No. 1El "apretón de manos" con láser forma una fuente de calor espacialmente sinusoidal, cuyo período (
L ) está determinado por el patrón de interferencia óptica.
Debido a la radiación térmica, se forma una "red térmica", un campo de temperatura espacialmente sinusoidal a lo largo de la superficie de la muestra (∆T (t, z) cos (qx), donde q = 2π / L es el vector de onda de la red térmica). Posteriormente, debido a la transferencia de calor, esta rejilla de calor decae. La expansión térmica crea una modulación sinusoidal acoplada del desplazamiento superficial o "pulsación" u (t) cos (qx), que actúa como una rejilla de difracción de transición para la radiación láser. Por lo tanto, la atenuación (decaimiento) de la rejilla de calor debido a la transferencia de calor está controlada por la difracción dependiente del tiempo del láser de sonda de onda continua. El haz difractado se superpone al haz de referencia de la misma fuente para la detección óptica de heterodino.
El grafito pirolítico altamente orientado fue el protagonista de este estudio, es decir, una muestra. La muestra era un policristal con un tamaño de grano de ~ 10 μm, y la posición del eje de todos los granos era perpendicular a la superficie de la muestra misma.
Inicialmente, se usó luz de 515 nm en la muestra para crear la rejilla térmica inicial a una profundidad de piel óptica de ~ 30 nm. El proceso de transferencia de calor se realizó en dos direcciones: a lo largo de la superficie de la rejilla de calor (en el plano) y perpendicular a la superficie (plano transversal). La transferencia de calor en el plano transversal del grafito fue ~ 300 veces más débil que la transferencia en el plano. Por lo tanto, la profundidad de difusión térmica en el plano transversal es mucho menor que la posición de la red de calor.
De acuerdo con la difusión de calor (τ =
L 2 / 4π
2 ⍺), en un medio unidimensional, la red de calor de transición decae exponencialmente. Esta afirmación se confirmó en la práctica: a una temperatura de 300 K, se detectaron signos de descomposición exponencial (
1B ). En
L (período de red) igual a 37,5 μm, se obtuvo una difusividad térmica de 11 cm
2 / s.
Con una disminución en el período de la red, la fórmula de difusión de calor dada anteriormente no corresponde a un valor constante de ⍺ (difusividad térmica). Cuanto más corto es el período de la red, más lenta es la descomposición / atenuación de la red térmica de transición (
1C ). Y esto está en desacuerdo con las predicciones del modelo de difusión de transferencia de calor.
Imagen No. 2El gráfico
2A muestra cambios significativos cuando la temperatura cae a 85 K. A una temperatura de 300 K, las señales se humedecen monótonamente, pero a 85 K, se producen oscilaciones amortiguadas cuando la señal puede caer por debajo de cero. Para la detección heterodina, un cambio en el signo de la señal de transición de la red de calor significa que la fase espacial de la red se ha desplazado por π. En otras palabras, la posición de los máximos y mínimos locales de los desplazamientos superficiales (incluida la temperatura) se invierte. Y este comportamiento de la rejilla térmica de transición es comparable a la
onda térmica
estacionaria * .
La onda estacionaria * es un proceso de onda en sistemas oscilatorios distribuidos con máximos y mínimos de amplitud alterna y estable en el espacio.
En la versión de difusión, la transferencia de calor ocurre de áreas más calientes a más frías, y los máximos y mínimos no pueden intercambiarse. Es decir, esta observación es una característica distintiva de la propagación del calor por las olas.
El recuadro en el gráfico
2A muestra que a medida que aumenta el período de la red, la frecuencia de la dinámica ondulatoria disminuye. La relación lineal observada indica una velocidad de 3200 m / s. Esta es una observación importante, ya que a menudo las señales de rejilla térmica de transición pueden contener oscilaciones debido a las ondas acústicas de la superficie, pero su velocidad es mucho menor. Dado que la velocidad de las ondas acústicas de la superficie es de aproximadamente 1480 m / s, que está cerca de la velocidad transversal lenta, mientras que la velocidad transversal rápida es de 14700 m / s, y la velocidad longitudinal es aún mayor. También vale la pena señalar que si hubiera ondas acústicas, no desaparecerían con un aumento en la temperatura de fondo o el período de celosía.
Para simular dicha dinámica, los científicos aplicaron la ecuación de transporte de Boltzmann linealizada con una matriz de dispersión de tres fonones completa en una red de calor de transición unidimensional. Anteriormente, se usaba un método similar para determinar la conductividad térmica de grafeno y grafito. Sin embargo, esta técnica era algo limitada y no podría aplicarse si no fuera por nuevos estudios que describieran un método para calcular la frecuencia de las funciones de Green para el transporte de Boltzmann inestable e inhomogéneo. La figura
2B muestra con precisión estas funciones verdes que describen la reacción de una población de fonones a una fuente de calor en forma de onda plana armónica.
Los cálculos realizados por los científicos teniendo en cuenta los métodos anteriores permitieron comprender la dependencia del tiempo de la amplitud de la rejilla térmica. Los cálculos a una temperatura de 300 K y varios períodos de celosía mostraron la atenuación exponencial de la celosía térmica de transición, que es totalmente consistente con el experimento (
1C ). A una temperatura de 85 K, la función de frecuencia de Green da un pico resonante (
2B ), que es un sello distintivo del segundo sonido y conduce a oscilaciones de amortiguación (
2C ). Todos los datos calculados son completamente comparables con los experimentales, incluso el hecho de la desaparición del segundo sonido en grandes períodos de la red térmica de transición.
Los cálculos mostraron que la velocidad del segundo sonido (teniendo en cuenta la posición del pico de la resonancia de frecuencia a
2C ) es 3650 m / s. Tal indicador distingue el grafito de una serie de otros materiales donde se detectó un segundo sonido. En ellos, la velocidad del segundo sonido era más lenta que la velocidad mínima de los fonones. El grafito también es sorprendente porque tiene una velocidad muy baja del modo acústico transversal lento. Y la impresionante anarmonía y la densidad de los estados de este modo conducen a una dispersión normal intensa y crean condiciones para la transferencia hidrodinámica de los fonones.
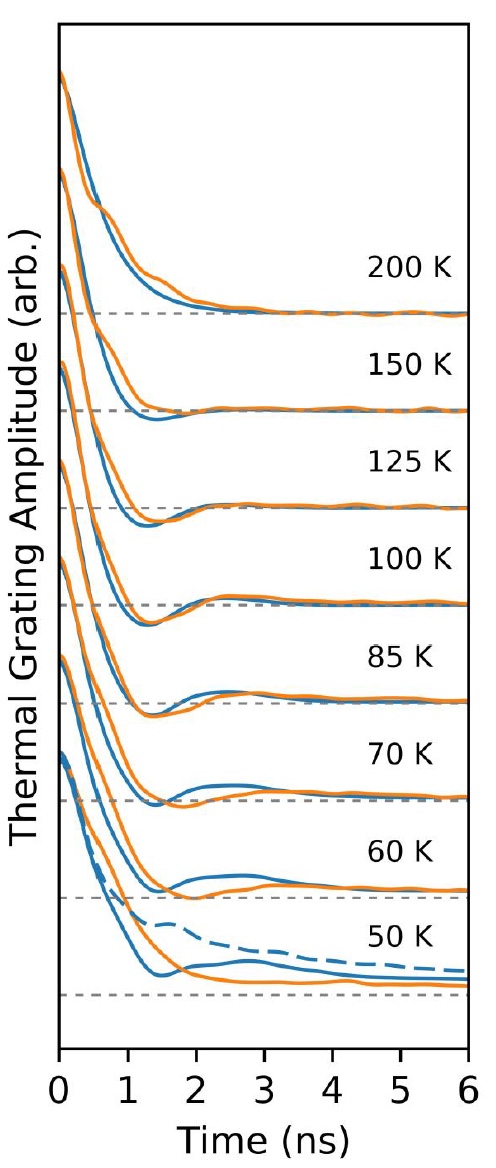Imagen No. 3El gráfico anterior (
No. 3 ) muestra los datos de la rejilla térmica de transición en un período constante de 10 μm y a diferentes temperaturas. Se observó un comportamiento vibratorio a 104 K e incluso a 125 K, pero cuando alcanza una temperatura de 150 K, desaparece por completo. Lo mismo sucede cuando la temperatura cae por debajo de 50 K.
El gráfico también muestra una respuesta simulada a 50 K en el modo balístico, cuando la tasa de dispersión de fonones se estableció en cero. Y aquí está claro que la falla en la respuesta en modo balístico desaparece. Es decir, la desaparición del segundo sonido a una temperatura de 50 K corresponde a lo que se espera durante la transición al modo balístico.
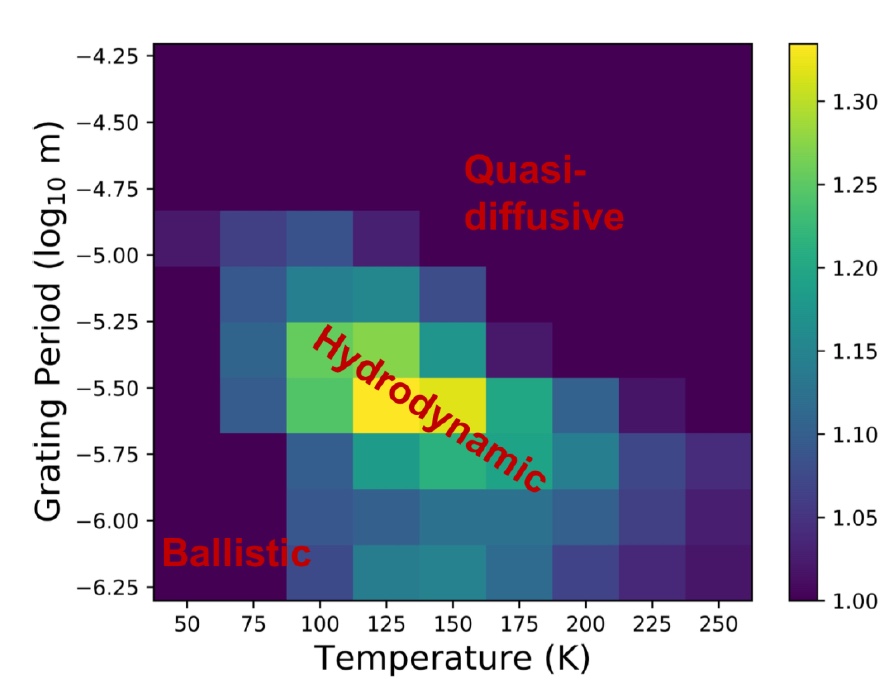Imagen No. 4El modelado de los datos mostró que se puede esperar la aparición de un segundo sonido en el rango de temperatura de 50 a 250 K. Cuanto mayor sea la temperatura, menor será la longitud de transferencia de calor: a
L = 10 μm, la temperatura "techo" es de aproximadamente 150 K, pero ya a
L = 1.5 μm se observará un segundo sonido hasta 250 K.
A bajas temperaturas y cortos períodos de celosía, la dispersión de fonones desaparece y la transferencia de calor se vuelve balística. Si hay altas temperaturas y largos períodos, la transferencia de calor pasa lentamente al modo de "cuasidifusión".
El grafito también se destacó en términos de isótopos. Es decir, antes el segundo sonido se observó solo en sólidos isotópicamente puros (si no se tienen en cuenta, según los científicos, las observaciones en SrTiO
3 no se tienen en cuenta). Pero el grafito utilizado en el experimento no es isotópicamente puro, lo que indica la naturaleza única de la hidrodinámica fonónica de esta sustancia.
Para un conocimiento más detallado de los matices, detalles, metodología y cálculos del estudio, le recomiendo que consulte el
informe de los científicos y los materiales adicionales .
Epílogo
A veces, los fenómenos o propiedades exóticos están ocultos en los objetos más comunes y poco notables. Este estudio fue una confirmación de esto. El segundo sonido, al ser un fenómeno exótico, se observó anteriormente solo en sustancias muy "extrañas" y en condiciones muy extremas.
Los científicos consideran que su trabajo es importante para el estudio general de la hidrodinámica de fonones. La comprensión de tales cosas permitirá utilizar grafito y grafeno como materiales disipadores de calor en microelectrónica. Los científicos también creen que su trabajo acelerará el estudio de la manipulación y el control de los procesos de transporte en la micro y nanoescala.
Sabemos mucho sobre las cosas que nos rodean, pero al mismo tiempo, tales estudios sugieren lo contrario. ¿Hay un límite para este conocimiento? Mientras exista la curiosidad y el entusiasmo de los científicos, no.
Gracias por su atención, sigan curiosos y tengan una buena semana laboral, muchachos.
Gracias por quedarte con nosotros. ¿Te gustan nuestros artículos? ¿Quieres ver más materiales interesantes?
Apóyenos haciendo un pedido o recomendándolo a sus amigos, un
descuento del 30% para los usuarios de Habr en un análogo único de servidores de nivel de entrada que inventamos para usted: toda la verdad sobre VPS (KVM) E5-2650 v4 (6 núcleos) 10GB DDR4 240GB SSD 1Gbps de $ 20 o cómo dividir el servidor? (las opciones están disponibles con RAID1 y RAID10, hasta 24 núcleos y hasta 40GB DDR4).
VPS (KVM) E5-2650 v4 (6 núcleos) 10GB DDR4 240GB SSD 1Gbps hasta el verano gratis al pagar por un período de seis meses, puede ordenar
aquí .
Dell R730xd 2 veces más barato? ¡Solo tenemos
2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV desde $ 249 en los Países Bajos y los Estados Unidos! Lea sobre
Cómo construir un edificio de infraestructura. clase utilizando servidores Dell R730xd E5-2650 v4 que cuestan 9,000 euros por un centavo?