Como regla general, las modificaciones a los algoritmos que dependen de las características específicas de una tarea en particular se consideran menos valiosas, ya que son difíciles de generalizar a una clase más amplia de problemas. Sin embargo, esto no significa que tales modificaciones no sean necesarias. Además, a menudo pueden mejorar significativamente el resultado incluso para problemas clásicos simples, lo cual es muy importante en la aplicación práctica de algoritmos. Como ejemplo, en esta publicación resolveré el problema del Mountain Car usando entrenamiento de refuerzo y mostraré que usando el conocimiento de cómo se organiza la tarea, se puede resolver mucho más rápido.
Sobre mi
Mi nombre es Oleg Svidchenko, ahora estoy estudiando en la Facultad de Ciencias Físicas, Matemáticas e Informática del HSE de San Petersburgo, antes estudié en la Universidad de San Petersburgo durante tres años. También trabajo en JetBrains Research como investigador. Antes de ingresar a la universidad, estudié en el SSC de la Universidad Estatal de Moscú y me convertí en el ganador de la Olimpiada de Rusia de niños en edad escolar en informática como parte del equipo de Moscú.
Que necesitamos
Si está interesado en probar el entrenamiento de refuerzo, el desafío Mountain Car es excelente para esto. Hoy necesitamos Python con las
bibliotecas Gym y
PyTorch instaladas, así como conocimientos básicos de redes neuronales.
Descripción de la tarea
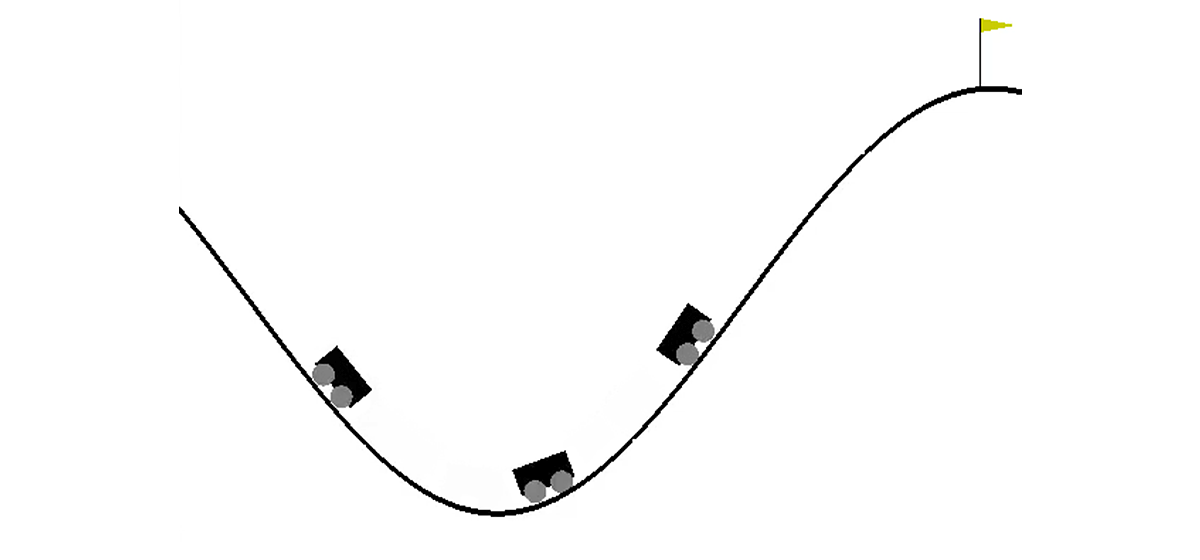
En un mundo bidimensional, un automóvil debe subir desde el hueco entre dos colinas hasta la cima de la colina derecha. Es complicado por el hecho de que ella no tiene suficiente potencia del motor para superar la fuerza de la gravedad y entrar allí en el primer intento. Estamos invitados a entrenar a un agente (en nuestro caso, una red neuronal), que puede, al controlarlo, subir la colina derecha lo más rápido posible.
El control de la máquina se lleva a cabo a través de la interacción con el entorno. Se divide en episodios independientes, y cada episodio se lleva a cabo paso a paso. En cada paso, el agente recibe los estados y el entorno
r del entorno en respuesta a la acción
a . Además, a veces el medio también puede informar que el episodio ha terminado. En este problema,
s es un par de números, el primero de los cuales es la posición del automóvil en la curva (una coordenada es suficiente, ya que no podemos separarnos de la superficie), y el segundo es su velocidad en la superficie (con un signo). La recompensa
r es un número siempre igual a -1 para esta tarea. De esta manera, alentamos al agente a completar el episodio lo más rápido posible. Solo hay tres acciones posibles: empujar el automóvil hacia la izquierda, no hacer nada y empujar el automóvil hacia la derecha. Estas acciones corresponden a números del 0 al 2. El episodio puede terminar si el automóvil llega a la cima de la colina derecha o si el agente ha dado 200 pasos.
Poco de teoría
En Habré ya había un
artículo sobre DQN en el que el autor describía bastante bien toda la teoría necesaria. Sin embargo, para facilitar la lectura, lo repetiré aquí en una forma más formal.
La tarea de aprendizaje de refuerzo se define por un conjunto de espacio de estado S, espacio de acción A, coeficiente
, las funciones de transición T y las funciones de recompensa R. En general, la función de transición y la función de recompensa pueden ser variables aleatorias, pero ahora consideraremos una versión más simple en la que se definen de manera única. El objetivo es maximizar las recompensas acumulativas.
, donde t es el número de paso en el medio y T es el número de pasos en el episodio.
Para resolver este problema, definimos la función de valor V del estado s como el valor de la recompensa acumulativa máxima, siempre que comencemos en el estado s. Conociendo dicha función, podemos resolver el problema simplemente pasando en cada paso a s con el máximo valor posible. Sin embargo, no todo es tan simple: en la mayoría de los casos, no sabemos qué acción nos llevará al estado deseado. Por lo tanto, agregamos la acción a como el segundo parámetro de la función. La función resultante se llama función Q. Muestra qué recompensa acumulativa máxima posible podemos obtener realizando la acción a en el estado s. Pero ya podemos usar esta función para resolver el problema: estando en estado s, simplemente elegimos un tal que Q (s, a) sea máximo.
En la práctica, no conocemos la función Q real, pero podemos aproximarla por varios métodos. Una de esas técnicas es la red Deep Q (DQN). Su idea es que para cada una de las acciones aproximamos la función Q utilizando una red neuronal.
El medio ambiente
Ahora vamos a practicar. Primero, necesitamos aprender a emular el entorno MountainCar. La biblioteca Gym, que proporciona una gran cantidad de entornos de aprendizaje de refuerzo estándar, nos ayudará a hacer frente a esta tarea. Para crear un entorno, debemos llamar al método make en el módulo del gimnasio y pasarle el nombre del entorno deseado como parámetro:
import gym env = gym.make("MountainCar-v0")
La documentación detallada se puede encontrar
aquí , y una descripción del entorno se puede encontrar
aquí .
Consideremos con más detalle lo que podemos hacer con el entorno que creamos:
env.reset() : finaliza el episodio actual y comienza uno nuevo. Devuelve el estado inicial.env.step(action) : realiza la acción especificada. Devuelve un nuevo estado, una recompensa, si el episodio ha finalizado e información adicional que puede usarse para la depuración.env.seed(seed) : establece una semilla aleatoria. Depende de cómo se generarán los estados iniciales durante env.reset ().env.render() : muestra el estado actual del entorno.
Nos damos cuenta DQN
DQN es un algoritmo que usa una red neuronal para evaluar una función Q. En el
artículo original, DeepMind definió la arquitectura estándar para los juegos de Atari utilizando redes neuronales convolucionales. A diferencia de estos juegos, Mountain Car no usa la imagen como un estado, por lo que tendremos que determinar la arquitectura nosotros mismos.
Tomemos, por ejemplo, una arquitectura con dos capas ocultas de 32 neuronas en cada una. Después de cada capa oculta, utilizaremos
ReLU como función de activación. Dos números que describen el estado se alimentan a la entrada de la red neuronal, y en la salida obtenemos una estimación de la función Q.
import torch.nn as nn model = nn.Sequential( nn.Linear(2, 32), nn.ReLU(), nn.Linear(32, 32), nn.ReLU(), nn.Linear(32, 3) ) target_model = copy.deepcopy(model)
Como entrenaremos la red neuronal en la GPU, debemos cargar nuestra red allí:
La variable del dispositivo será global, ya que también necesitaremos cargar los datos.
También necesitamos definir un optimizador que actualice los pesos del modelo usando el descenso de gradiente. Sí, hay muchos más que uno.
optimizer = optim.Adam(model.parameters(), lr=0.00003)
Todos juntos import torch.nn as nn import torch device = torch.device("cuda") def create_new_model(): model = nn.Sequential( nn.Linear(2, 32), nn.ReLU(), nn.Linear(32, 32), nn.ReLU(), nn.Linear(32, 3) ) target_model = copy.deepcopy(model)
Ahora declaramos una función que considerará la función de error, el gradiente a lo largo de ella, y aplicaremos el descenso. Pero antes de eso, debe descargar los datos del lote a la GPU:
state, action, reward, next_state, done = batch
A continuación, necesitamos calcular los valores reales de la función Q, sin embargo, dado que no los conocemos, los evaluaremos a través de los valores para el siguiente estado:
target_q = torch.zeros(reward.size()[0]).float().to(device) with torch.no_grad():
Y la predicción actual:
q = model(state).gather(1, action.unsqueeze(1))
Usando target_q y q, calculamos la función de pérdida y actualizamos el modelo:
loss = F.smooth_l1_loss(q, target_q.unsqueeze(1))
Todos juntos gamma = 0.99 def fit(batch, model, target_model, optimizer): state, action, reward, next_state, done = batch
Dado que el modelo solo considera la función Q, y no realiza acciones, necesitamos determinar la función que decidirá qué acciones realizará el agente. Como algoritmo de toma de decisiones, tomamos
-política política. Su idea es que el agente generalmente realiza acciones con avidez, eligiendo el máximo de la función Q, pero con probabilidad
él tomará una acción al azar. Se necesitan acciones aleatorias para que el algoritmo pueda examinar aquellas acciones que no habría llevado a cabo guiado solo por una política codiciosa; este proceso se llama exploración.
def select_action(state, epsilon, model): if random.random() < epsilon: return random.randint(0, 2) return model(torch.tensor(state).to(device).float().unsqueeze(0))[0].max(0)[1].view(1, 1).item()
Dado que usamos lotes para entrenar la red neuronal, necesitamos un búfer en el que almacenaremos la experiencia de interactuar con el entorno y desde donde elegiremos lotes:
class Memory: def __init__(self, capacity): self.capacity = capacity self.memory = [] self.position = 0 def push(self, element): """ """ if len(self.memory) < self.capacity: self.memory.append(None) self.memory[self.position] = element self.position = (self.position + 1) % self.capacity def sample(self, batch_size): """ """ return list(zip(*random.sample(self.memory, batch_size))) def __len__(self): return len(self.memory)
Decisión ingenua
Primero, declare las constantes que utilizaremos en el proceso de aprendizaje y cree un modelo:
A pesar del hecho de que sería lógico dividir el proceso de interacción en episodios, para describir el proceso de aprendizaje, es más conveniente para nosotros dividirlo en pasos separados, ya que queremos dar un paso de descenso de gradiente después de cada paso del entorno.
Hablemos con más detalle sobre cómo se ve aquí un paso del aprendizaje. Suponemos que ahora estamos dando un paso con el número de pasos max_steps y el estado actual. Luego haciendo la acción con
las políticas de greedy se verían así:
epsilon = max_epsilon - (max_epsilon - min_epsilon)* step / max_steps action = select_action(state, epsilon, model) new_state, reward, done, _ = env.step(action)
Agregue inmediatamente la experiencia adquirida a la memoria y comience un nuevo episodio si el actual ha finalizado:
memory.push((state, action, reward, new_state, done)) if done: state = env.reset() done = False else: state = new_state
Y tomaremos el paso de descenso gradual (si, por supuesto, ya podemos recolectar al menos un lote):
if step > batch_size: fit(memory.sample(batch_size), model, target_model, optimizer)
Ahora queda por actualizar target_model:
if step % target_update == 0: target_model = copy.deepcopy(model)
Sin embargo, también nos gustaría seguir el proceso de aprendizaje. Para hacer esto, jugaremos un episodio adicional después de cada actualización de target_model con epsilon = 0, almacenando la recompensa total en el búfer rewards_by_target_updates:
if step % target_update == 0: target_model = copy.deepcopy(model) state = env.reset() total_reward = 0 while not done: action = select_action(state, 0, target_model) state, reward, done, _ = env.step(action) total_reward += reward done = False state = env.reset() rewards_by_target_updates.append(total_reward)
Ejecute este código y obtenga algo como este gráfico:
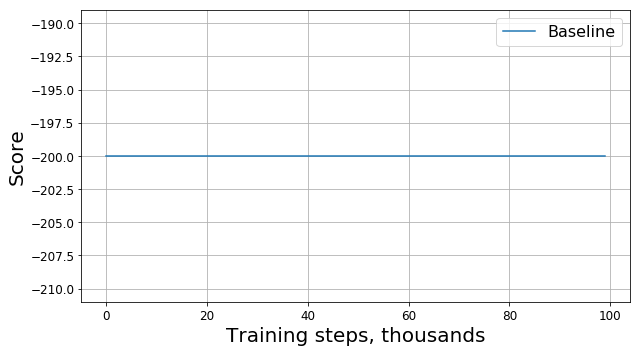
¿Qué salió mal?
¿Es esto un error? ¿Es este el algoritmo incorrecto? ¿Son estos malos parámetros? En realidad no De hecho, el problema está en la tarea, es decir, en la función de la recompensa. Miremos más de cerca. En cada paso, nuestro agente recibe una recompensa de -1, y esto sucede hasta que finaliza el episodio. Tal recompensa motiva al agente a completar el episodio lo más rápido posible, pero al mismo tiempo no le dice cómo hacerlo. Debido a esto, la única forma de aprender cómo resolver un problema en una formulación de este tipo para un agente es resolverlo muchas veces utilizando la exploración.
Por supuesto, uno podría intentar usar algoritmos más complejos para estudiar el entorno en lugar del nuestro
-políticas políticas. Sin embargo, en primer lugar, debido a su aplicación, nuestro modelo se volverá más complejo, lo que nos gustaría evitar, y en segundo lugar, no el hecho de que funcionarán lo suficientemente bien para esta tarea. En cambio, podemos eliminar la fuente del problema modificando la tarea en sí, es decir, cambiando la función de recompensa, es decir aplicando lo que se llama dar forma a la recompensa.
Acelerar la convergencia
Nuestro conocimiento intuitivo nos dice que para conducir cuesta arriba necesitas acelerar. Cuanto mayor sea la velocidad, más cerca estará el agente de resolver el problema. Puede contarle sobre esto, por ejemplo, agregando un módulo de velocidad con un cierto coeficiente a la recompensa:
recompensa modificada = recompensa + 10 * abs (nuevo_estado [1])
En consecuencia, una línea en la función encaja
memory.push ((estado, acción, recompensa, nuevo_estado, hecho))
debe ser reemplazado por
memory.push ((estado, acción, recompensa modificada, nuevo_estado, hecho))
Ahora veamos el nuevo cuadro (presenta el premio
original sin modificaciones):
 Aquí RS es la abreviatura de Reward Shaping.
Aquí RS es la abreviatura de Reward Shaping.¿Es bueno hacer esto?
El progreso es obvio: nuestro agente claramente aprendió a conducir cuesta arriba, ya que el premio comenzó a diferir de -200. Solo queda una pregunta: si al cambiar la función de la recompensa, también cambiamos la tarea en sí, ¿la solución al nuevo problema que encontramos será buena para el viejo problema?
Para empezar, entendemos lo que significa "bondad" en nuestro caso. Para resolver el problema, estamos tratando de encontrar la política óptima, una que maximice la recompensa total por el episodio. En este caso, podemos reemplazar la palabra "bueno" por la palabra "óptimo", porque lo estamos buscando. También esperamos de manera optimista que tarde o temprano nuestro DQN encuentre la solución óptima para el problema modificado y no se quede atascado en un máximo local. Entonces, la pregunta puede reformularse de la siguiente manera: si al cambiar la función de la recompensa, también cambiamos el problema en sí, ¿será la solución óptima para el nuevo problema que encontramos óptimo para el viejo problema?
Como resultado, no podemos proporcionar tal garantía en el caso general. La respuesta depende de cómo cambiamos exactamente la función de la recompensa, cómo se organizó antes y cómo se organiza el entorno en sí. Afortunadamente, hay
un artículo cuyos autores investigaron cómo el cambio de la función de la recompensa afecta la optimización de la solución encontrada.
Primero, encontraron toda una clase de cambios "seguros" que se basan en el método potencial:
donde
- potencial, que depende solo del estado. Para tales funciones, los autores pudieron demostrar que si la solución para el nuevo problema es óptima, para el problema anterior también es óptima.
En segundo lugar, los autores demostraron que para cualquier otro
existe tal problema, la función de recompensa R y la solución óptima para el problema modificado, que esta solución no es óptima para el problema original. Esto significa que no podemos garantizar la bondad de la solución que encontramos si utilizamos un cambio que no se basa en el método potencial.
Por lo tanto, el uso de funciones potenciales para modificar la función de recompensa solo puede cambiar la tasa de convergencia del algoritmo, pero no afecta la solución final.
Acelera la convergencia correctamente
Ahora que sabemos cómo cambiar la recompensa de manera segura, intentemos modificar la tarea nuevamente, utilizando el método potencial en lugar de la heurística ingenua:
recompensa modificada = recompensa + 300 * (gamma * abs (nuevo_estado [1]) - abs (estado [1]))
Veamos el cronograma del premio original:

Al final resultó que, además de tener garantías teóricas, la modificación de la recompensa con la ayuda de funciones potenciales también mejoró significativamente el resultado, especialmente en las primeras etapas. Por supuesto, existe la posibilidad de que sea posible seleccionar hiperparámetros más óptimos (semilla aleatoria, gamma y otros coeficientes) para entrenar al agente, sin embargo, la conformación de recompensas aún aumenta significativamente la tasa de convergencia del modelo.
Epílogo
¡Gracias por leer hasta el final! Espero que hayan disfrutado esta pequeña excursión orientada a la práctica en el aprendizaje reforzado. Está claro que Mountain Car es una tarea de "juguete", sin embargo, como pudimos notar, enseñarle a un agente a resolver incluso una tarea aparentemente tan simple desde un punto de vista humano puede ser difícil.